Ορισμός 9.2
Μια context free γραμματική 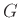 πάνω από ένα αλφάβητο
πάνω από ένα αλφάβητο 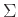 (τα τερματικά σύμβολα) είναι μια πεπερασμένη συλλογή από
(τα τερματικά σύμβολα) είναι μια πεπερασμένη συλλογή από
-
μη τερματικά σύμβολα,
που συνήθως τα συμβολίζουμε με κεφαλαία λατινικά γράμματα,
και που περιλαμβάνουν το διακεριμένο σύμβολο
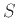 (αρχικό
μη τερματικό σύμβολο)
(αρχικό
μη τερματικό σύμβολο)
-
κανόνες παραγωγής
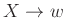 , όπου
, όπου 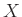 είναι ένα μη τερματικό σύμβολο
και
είναι ένα μη τερματικό σύμβολο
και 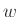 είναι μια λέξη από γράμματα του
είναι μια λέξη από γράμματα του 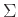 και μη τερματικά σύμβολα
(η
και μη τερματικά σύμβολα
(η 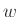 μπορεί να είναι και η κενή λέξη).
μπορεί να είναι και η κενή λέξη).
Αν 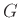 είναι μια Context Free Grammar(CFG), Context Free Γραμματική, και
είναι μια Context Free Grammar(CFG), Context Free Γραμματική, και
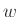 .
.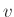 είναι δύο λέξεις από τερματικά ή μη τερματικά σύμβολα,
τότε γράφουμε
είναι δύο λέξεις από τερματικά ή μη τερματικά σύμβολα,
τότε γράφουμε
αν με χρήση ενός κανόνα παραγωγής
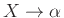 μπορεί να προκύψει
η λέξη
μπορεί να προκύψει
η λέξη 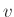 από τη λέξη
από τη λέξη 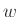 . Αυτό σημαίνει ότι αντικαθιστούμε μια εμφάνιση
του μη τερματικού συμβόλου
. Αυτό σημαίνει ότι αντικαθιστούμε μια εμφάνιση
του μη τερματικού συμβόλου 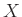 στη λέξη
στη λέξη 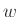 με τη λέξη
με τη λέξη 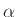 (που απαρτίζεται
από τερματικά και μη τερματικά σύμβολα) και με την αντικατάσταση αυτή προκύπτει
η λέξη
(που απαρτίζεται
από τερματικά και μη τερματικά σύμβολα) και με την αντικατάσταση αυτή προκύπτει
η λέξη 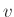 .
.
Για παράδειγμα, αν 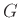 είναι η γραμματική που ορίσαμε παραπάνω τότε
ισχύει
είναι η γραμματική που ορίσαμε παραπάνω τότε
ισχύει
μια και από την αριστερή λέξη προκύπτει η δεξιά αν χρησιμοποιηθεί
ο κανόνας 2.
Ορίζουμε επίσης
να σημαίνει ότι υπάρχει πεπερασμένη ακολουθία λέξεων
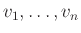 ώστε
ώστε
ότι δηλ. η λέξη 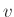 μπορεί να προκύψει από τη λέξη
μπορεί να προκύψει από τη λέξη 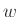 με επανειλημμένη
χρήση των κανόνων παραγωγής της
με επανειλημμένη
χρήση των κανόνων παραγωγής της 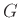 .
Στην παραπάνω γραμματική για τις εκφράσεις ισχύει, για παράδειγμα,
.
Στην παραπάνω γραμματική για τις εκφράσεις ισχύει, για παράδειγμα,
αφού μπορούμε από τη λέξη 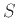 να πάμε στη λέξη
να πάμε στη λέξη 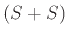 εφαρμόζοντας
πρώτα τον κανόνα 3 και μετά τον κανόνα 2.
εφαρμόζοντας
πρώτα τον κανόνα 3 και μετά τον κανόνα 2.
Έχοντας στα χέρια μας τον συμβολισμό αυτό μπορούμε εύκολα
να ορίσουμε πλέον ποια είναι η γλώσσα που αντιστοιχεί σε
μια λέξη (από τερματικά ή μη σύμβολα).
Απαρτίζεται δηλ. η 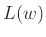 από εκείνες τις λέξεις χωρίς μη τερματικά
σύμβολα που μπορούν να παραχθούν σε πεπερασμένο πλήθος βημάτων από τη
λέξη
από εκείνες τις λέξεις χωρίς μη τερματικά
σύμβολα που μπορούν να παραχθούν σε πεπερασμένο πλήθος βημάτων από τη
λέξη 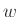 με τους κανόνες παραγωγής της
με τους κανόνες παραγωγής της 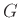 .
.
Τέλος ορίζουμε την γλώσσα της 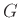 .
.
Ορισμός 9.4
Αν 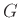 είναι μια CFG η γλώσσα
είναι μια CFG η γλώσσα 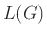 ορίζεται να είναι η γλώσσα
ορίζεται να είναι η γλώσσα 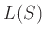 .
Μια γλώσσα
.
Μια γλώσσα 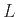 λέγεται Context Free Language (CFL), Context Free Γλώσσα, αν είναι η γλώσσα
κάποιας context free γραμματικής.
λέγεται Context Free Language (CFL), Context Free Γλώσσα, αν είναι η γλώσσα
κάποιας context free γραμματικής.
Είναι δηλ. η γλώσσα της 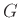 όλες οι λέξεις του
όλες οι λέξεις του 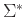 που παράγονται
από το αρχικό μη τερματικό σύμβολο
που παράγονται
από το αρχικό μη τερματικό σύμβολο 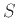 .
.
Θα χρησιμοποιούμε συνήθως τη συντομογραφία
για να υποδηλώσουμε μια ομάδα από κανόνες παραγωγής
με το ίδιο αριστερό μέλος.
Άσκηση 9.1
Ποια είναι η γλώσσα της γραμματικής
με κανόνες
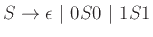 ;
;
Άσκηση 9.2
Δώστε μια CFG για τη γλώσσα
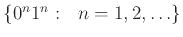 .
.
Άσκηση 9.3
Ανατρέξτε πίσω στον ορισμό του τι είναι κανονική έκφραση.
Αν σταθεροποιήσουμε το αλφάβητο σε, ας πούμε,
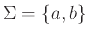 ,
δώστε μια CFG για τη γλώσσα των κανονικών εκφράσεων
πάνω από το
,
δώστε μια CFG για τη γλώσσα των κανονικών εκφράσεων
πάνω από το 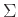 .
.
Mihalis Kolountzakis
2015-11-28
![]() είναι μια Context Free Grammar(CFG), Context Free Γραμματική, και
είναι μια Context Free Grammar(CFG), Context Free Γραμματική, και
![]() .
.![]() είναι δύο λέξεις από τερματικά ή μη τερματικά σύμβολα,
τότε γράφουμε
είναι δύο λέξεις από τερματικά ή μη τερματικά σύμβολα,
τότε γράφουμε
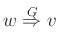
![]() είναι η γραμματική που ορίσαμε παραπάνω τότε
ισχύει
είναι η γραμματική που ορίσαμε παραπάνω τότε
ισχύει
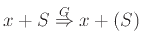
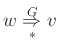
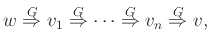
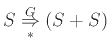
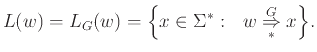
![]() .
.