ΑΣΚΗΣΗ 8Ελαστικές και μη ελαστικές κρούσεις
Αρχή διατήρησης της ορμής

  • Σύνοψη:
    Σκοπός της συγκεκριμένης άσκησης είναι η πειραματική επαλήθευση της Αρχής διατήρησης της ορμής σε ελαστική και μη ελαστική κρούση. Επιπλέον, θα υπολογίσεις το ποσοστό της αρχικής ενέργειας που μετατρέπεται σε θερμότητα κατά τις παραπάνω κρούσεις

    Τα όργανα που θα χρησιμοποιήσεις είναι: διάδρομος κίνησης 1,2 m, 2 αμαξίδια αμελητέας τριβής, 2 βαράκια 0,25 kg, 2 αισθητήρες κίνησης και Η/Υ.

  • Πιθανά οφέλη:
    Η εξοικείωση στη χρήση των Η/Υ για την οργάνωση και τη διεξαγωγή ενός πειράματος.

  • Προαπαιτούμενη γνώση:

ΘΕΩΡΙΑ

Γνωρίζουμε ότι η ορμή ενός υλικού σημείου (σώματος) είναι ένα διανυσματικό μέγεθος, ομόρροπο της ταχύτητας (Εικόνα 8.1).

Εικόνα 8.1 Ορμή υλικού σημείου.

Ορμή συστήματος σωμάτων
Ορμή συστήματος σωμάτων ορίζουμε το διανυσματικό άθροισμα των ορμών των σωμάτων (Young, 1994).

 Όταν σε ένα σύστημα σωμάτων η συνισταμένη των εξωτερικών δυνάμεων είναι μηδέν (ή αμελητέα), τότε η ολική ορμή του συστήματος δεν μεταβάλλεται. Λέμε ότι η ολική ορμή του συστήματος διατηρείται.

Έστω, λοιπόν, ότι το σύστημά μας αποτελείται από δύο αμαξίδια πάνω σε μια οριζόντια, λεία επιφάνεια. Αυτά, όπως φαίνεται στην Εικόνα 8.2, κινούνται το ένα προς το άλλο. Οι μόνες δυνάμεις που ασκούνται στο κάθε αμαξίδιο από σώματα που δεν ανήκουν στο σύστημα είναι η δύναμη της βαρύτητας από τη γη και η αντίδραση από την οριζόντια επιφάνεια, δυνάμεις οι οποίες αλληλοεξουδετερώνονται. Θεωρείς ότι η τριβή ανάμεσα στα αμαξίδια και την οριζόντια επιφάνεια, καθώς και η αντίσταση του αέρα είναι αμελητέες σε σχέση με τις άλλες δυνάμεις του πειράματος. Σε αυτό, λοιπόν, το σύστημα των σωμάτων η συνολική ορμή των αμαξιδίων δεν μεταβάλλεται πριν, κατά και μετά τη σύγκρουσή τους.

Εικόνα 8.2 Σχηματική αναπαράσταση πειραματικής διάταξης πριν τη σύγκρουση.

Η συνολική ορμή των αμαξιδίων πριν τη σύγκρουση είναι: \[ \overrightarrow{p}^{\alpha \rho \chi}=\overrightarrow{p_{_{_{1}}}}^{\alpha \rho \chi}+\overrightarrow{p_{_{_{2}}}}^{\alpha \rho \chi}\Rightarrow \overrightarrow{p}^{\alpha \rho \chi}=m_{1}\overrightarrow{\mathrm{v}_{_{_{1}}}}^{\alpha \rho \chi}+m_{2}\overrightarrow{\mathrm{v}_{_{_{2}}}}^{\alpha \rho \chi}\]
(8.1)

Το μέτρο, λοιπόν, της ορμής ως προς το θετικό ημιάξονα πριν τη σύγκρουση είναι: \[p^{\alpha \rho \chi }=m_{1}\mathrm{v}_{_{1}}^{\alpha \rho \chi }-m_{2}\mathrm{v}_{_{2}}^{\alpha \rho \chi}\]
(8.2)

Η ορμή κάθε αμαξιδίου είναι διανυσματικό μέγεθος, οπότε η κατεύθυνσή της παίζει σημαντικό ρόλο στον υπολογισμό του μέτρου της συνολικής ορμής του συστήματος. Όταν το διάνυσμα της ταχύτητας, άρα και της ορμής, κάποιου αμαξιδίου δείχνει προς την κατεύθυνση του άξονα την οποία διαλέγουμε ως θετική, στον υπολογισμό του μέτρου της συνολικής ορμής η ορμή εμφανίζεται με θετικό πρόσημο. Όταν το διάνυσμα της ταχύτητας δείχνει προς την αντίθετη κατεύθυνση, δηλαδή την αρνητική, η ορμή είναι αρνητική και αφαιρείται.
Η κινητική ενέργεια των αμαξιδίων πριν τη σύγκρουση είναι: \[K^{\alpha \rho \chi }=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{\alpha \rho \chi })^2+\frac{1}{2}m_{2}(\mathrm{v}_{_{2}}^{\alpha \rho \chi })^2\]
(8.3)

Μετά τη σύγκρουση (βλ. Εικόνα 8.3) η ορμή του συστήματος είναι: \[\overrightarrow{p}^{\tau \epsilon \lambda }=\overrightarrow{p_{_{_{1}}}}^{\tau \epsilon \lambda }+\overrightarrow{p_{_{_{2}}}}^{\tau \epsilon \lambda }\Rightarrow \overrightarrow{p}^{\tau \epsilon \lambda }=m_{1}\overrightarrow{\mathrm{v}_{_{_{1}}}}^{\tau \epsilon \lambda }+m_{2}\overrightarrow{\mathrm{v}_{_{_{2}}}}^{\tau \epsilon \lambda }\]
(8.4)

Εικόνα 8.3 Σχηματική αναπαράσταση πειραματικής διάταξη μετά τη σύγκρουση.

Το μέτρο της τελικής ορμής είναι: \[p^{\tau \epsilon \lambda }=m_{1}\mathrm{v}_{_{1}}^{\tau \epsilon \lambda }+m_{2}\mathrm{v}_{_{2}}^{\tau \epsilon \lambda }\]
(8.5)

Η κινητική ενέργεια των αμαξιδίων μετά τη σύγκρουση είναι: \[K^{\tau \epsilon \lambda }=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{\tau \epsilon \lambda })^2+\frac{1}{2}m_{2}(\mathrm{v}_{_{2}}^{\tau \epsilon \lambda })^2\]
(8.6)

    Είδη κρούσεων
  1. Αν η ολική κινητική ενέργεια των σωμάτων μετά τη σύγκρουση είναι ίδια με αυτήν πριν τη σύγκρουση (διατήρηση της κινητικής ενέργειας), έχουμε μια ελαστική κρούση.
  2. Αν μετά την κρούση η κινητική ενέργεια των σωμάτων είναι μικρότερη από πριν, μιλάμε για μη ελαστική κρούση. Μέρος της κινητικής ενέργειας που χάνεται μετατρέπεται σε θερμότητα ή σε ενέργεια παραμόρφωσης των αντικειμένων που συγκρούστηκαν.
  3. Ειδική περίπτωση μη ελαστικής κρούσης, κατά την οποία τα συγκρουόμενα σώματα γίνονται ένα συσσωμάτωμα, είναι η πλαστική κρούση.

ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ

Πειραματική διάταξη

Η διάταξη του πειράματος παρουσιάζεται σχηματικά στην Εικόνα 8.4.

Εικόνα 8.4 Σχηματική αναπαράσταση πειραματικής διάταξης.

Το αριστερό αμαξίδιο θα το ονομάζουμε αμαξίδιο 1 και το δεξιό αμαξίδιο 2.

Πειραματικό μέρος Α΄: Πλαστικές κρούσεις

  1. Για να εμφανιστεί το κατάλληλο πρόγραμμα στην οθόνη του Η/Υ, ανοίγεις από την επιφάνεια εργασίας το φάκελο MAGOS.

  2. Επιλέγεις το πρόγραμμα MAGOS που έχει τον ίδιο αριθμό με την άσκηση που θα κάνεις.

  3. Τοποθετείς τα δύο αμαξίδια πάνω στο διάδρομο κίνησης. Σε κάθε άκρη του διαδρόμου υπάρχει και από ένας αισθητήρας κίνησης ο οποίος μπορεί να καταγράφει τη θέση και την ταχύτητα κάθε αμαξιδίου. Για να είναι αξιόπιστες οι μετρήσεις των αισθητήρων, τα αμαξίδια πρέπει να βρίσκονται σε απόσταση μεγαλύτερη των 15 cm από αυτούς.

  4. Το αμαξίδιο 2 (αμαξίδιο-στόχος) θα έχει τη μεγαλύτερη μάζα. (Αυτό δεν είναι υποχρεωτικό.) Βάζεις πάνω του ένα βαράκι 0,25 kg και, στη συνέχεια, το τοποθετείς στο μέσο περίπου του διαδρόμου κίνησης.

  5. Τοποθετείς το αμαξίδιο 1 σε απόσταση 15 cm περίπου από τον αριστερό αισθητήρα κίνησης. Στο συγκεκριμένο πείραμα τα δύο αμαξίδια πρέπει, μετά την σύγκρουσή τους, να κολλήσουν και να συνεχίσουν να κινούνται ως ένα σώμα. Γι’ αυτό, λοιπόν, φρόντισε να τοποθετηθούν έτσι, ώστε η επιφάνεια επαφής τους κατά τη σύγκρουση να έχει το υλικό συγκόλλησης (κριτς-κρατς).

  6. Όταν είσαι έτοιμος, πατάς το κουμπί Start (αριστερό κλικ στο ποντίκι) και αμέσως μετά σπρώχνεις το αμαξίδιο 1 προς την κατεύθυνση του αμαξιδίου 2.

  7. Αφού τα αμαξίδια συγκρουστούν και, έπειτα, κινηθούν λίγο, πατάς Stop.

  8. Στην οθόνη του υπολογιστή θα καταγραφεί η γραφική παράσταση της ταχύτητας των αμαξιδίων ως συνάρτηση του χρόνου. Η Εικόνα 8.5 παρουσιάζει πώς θα είναι περίπου αυτή η γραφική παράσταση.

    9. Εικόνα 8.5 Γραφική παράσταση ταχύτητας στην οθόνη του υπολογιστή.

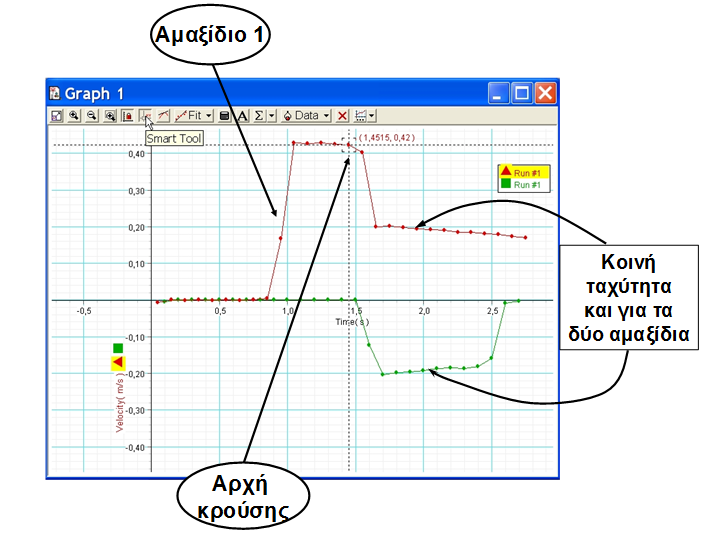
    Περιγραφή γραφικής παράστασης

    Το Data Studio ορίζει ως θετική την ταχύτητα ενός αμαξιδίου που απομακρύνεται από τον αισθητήρα και ως αρνητική, όταν το αμαξίδιο πλησιάζει σε αυτόν.

    Το αμαξίδιο 1 αρχικά είναι ακίνητο (κόκκινη γραμμή στην οθόνη). Λόγω της ώθησης που δέχεται από το χέρι σου, η ταχύτητά του αυξάνεται απότομα. Μόλις σταματήσει η ώθηση του χεριού, το αμαξίδιο συνεχίζει με -περίπου- σταθερή ταχύτητα. Κατά τη σύγκρουσή του με το αμαξίδιο 2 η ταχύτητά του μειώνεται.
    Το αμαξίδιο 2 είναι ακίνητο (πράσινη γραμμή στην οθόνη) μέχρι τη στιγμή της σύγκρουσής του με το αμαξίδιο 1. Κατά τη σύγκρουση η ταχύτητά του αυξάνεται κατά απόλυτη τιμή. Στη γραφική παράσταση φαίνεται να παίρνει αρνητικές τιμές, εφόσον το αμαξίδιο 2 πλησιάζει προς τον αισθητήρα 2.
    Μετά τη σύγκρουση τα δύο αμαξίδια κολλάνε και κινούνται με την ίδια ταχύτητα. Στην Εικόνα 8.5 οι ταχύτητες και για τα δύο αμαξίδια μετά την σύγκρουση είναι ίδιες κατά απόλυτη τιμή, αλλά διαφέρουν στο πρόσημο, αφού το συσσωμάτωμα των δύο αμαξιδίων απομακρύνεται από τον αριστερό αισθητήρα 1 και πλησιάζει προς το δεξιό αισθητήρα 2.

  9. Από αυτήν τη γραφική παράσταση υπολογίζεις την ταχύτητα \(\mathrm{v}_{_{1}}^{\alpha \rho \chi }\) του αμαξιδίου 1 και την ταχύτητα του συσσωματώματος των δύο αμαξιδίων \(\mathrm{v}^{\kappa o\iota \nu .}\) μετά τη σύγκρουση.

    10. Παρατήρηση (για την Εικόνα 8.5):
    Η κοινή ταχύτητα μετά την κρούση, αρχικά, παραμένει σταθερή. Μετά, όμως, παρουσιάζει μια κλίση που εκφράζει την επιβράδυνση που αρχίζει να εμφανίζεται λόγω των αντιστάσεων (τριβές κυρίως), και οι οποίες, πλέον, επηρεάζουν αισθητά την κίνηση του συσσωματώματος.

    Υπόδειξη για να βρεις τις ταχύτητες:
    Για να βρεις, για παράδειγμα, την \(\mathrm{v}_{_{1}}^{\alpha \rho \chi }\) , κάνεις αριστερό κλικ με το ποντίκι στο εικονίδιο Smart Tool (βλ. Εικόνα 8.5). Στην οθόνη σου θα εμφανιστεί ένα τετραγωνάκι. Το τετράγωνο αυτό, κάνοντας αριστερό κλικ με το ποντίκι πάνω του, μπορείς να το πιάσεις και να το μετακινήσεις όπου επιθυμείς πάνω στην καμπύλη της γραφικής σου παράστασης. Επειδή θέλουμε την ταχύτητα του αμαξιδίου αμέσως πριν τη σύγκρουσή του, μετακινείς το τετράγωνο στο τελευταίο σημείο της γραφικής παράστασης της ταχύτητας του αμαξιδίου 1 (κόκκινη γραμμή) πριν τη σύγκρουσή του. Στην οθόνη σου θα εμφανιστούν ο χρόνος και η ταχύτητα \(\mathrm{v}^{\alpha \rho \chi }\) του αμαξιδίου για το συγκεκριμένο σημείο, δηλ. οι συντεταγμένες του σημείου. Τα ίδια ισχύουν και για την κοινή ταχύτητα μετά την κρούση, με τη διαφορά ότι στην περίπτωση αυτή επιλέγεις το πρώτο σημείο αμέσως μετά το τέλος της κρούσης.

Βίντεο: Πλαστική κρούση


Βίντεο 8.1 Πείραμα της άσκησης 8.


Πειραματικό μέρος B΄: Ελαστικές κρούσεις

Μετά την ελαστική κρούση τα δύο αμαξίδια θα πρέπει να απομακρυνθούν μεταξύ τους. Γι’ αυτό, φρόντισε να τοποθετηθούν με τέτοιο τρόπο, ώστε η επιφάνεια επαφής τους κατά τη σύγκρουση να έχει τους μαγνήτες. Όταν, λοιπόν, πλησιάσεις το ένα στο άλλο, αυτά θα απωθούνται.
  1. Στο πείραμα της ελαστικής κρούσης το αμαξίδιο 2 (αμαξίδιο-στόχος) έχει μεγαλύτερη μάζα. Γι’ αυτό, τοποθετείς πάνω του βάρος 0,25kg. Χρησιμοποιείς το άλλο αμαξίδιο χωρίς επιπλέον βάρος.

  2. Ζυγίζεις τα 2 αμαξίδια και τα τοποθετείς στο διάδρομο κίνησης.

  3. Σπρώχνεις το αμαξίδιο 1 προς την κατεύθυνση του αμαξιδίου 2 και με τη βοήθεια του Data Studio καταγράφεις τις ταχύτητες των αμαξιδίων ως συνάρτηση του χρόνου. Βρίσκεις τις ταχύτητες των αμαξιδίων πριν και μετά την κρούση από τη γραφική παράσταση στην οθόνη του υπολογιστή.
Προαιρετικά
Μια ενδιαφέρουσα περίπτωση είναι αυτή όπου m1=m2, οπότε τα κινητά ανταλλάσουν ταχύτητες. Δε χρειάζεται να γράψεις στην αναφορά σου τα αποτελέσματα αυτών των πειραμάτων. Για να ξεκινήσεις τα πειράματα ελαστικών κρούσεων, καθαρίζεις το Data Studio από τα δεδομένα του πρώτου πειράματος πατώντας Experiment και επιλέγοντας Delete Last Data Run.


ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ

Θα γράψεις τα παρακάτω στο τετράδιο του εργαστηρίου πριν το πείραμα.

  • Τίτλος Άσκησης:
  • Όνομα:
  • Ημερομηνία:
  • Σκοπός:

Παρατήρηση: Εκτός από το τελικό αποτέλεσμα, να φαίνονται οι αντικαταστάσεις με τις μονάδες τους.

Πειραματικό μέρος Α΄: Πλαστικές κρούσεις

  1. Οι μάζες των αμαξιδίων είναι: \(\mathrm{m_{1}=.....10^{-3}kg}\), \(\mathrm{m_{2}=.....10^{-3}kg}\).

  2. Τα μέτρα των ταχυτήτων είναι: \[\mathrm{v}_{_{1}}^{\alpha \rho \chi }=.....\frac{m}{s}\] \[\mathrm{v}_{_{2}}^{\alpha \rho \chi} =0\frac{m}{s}\] \[\mathrm{v}^{\kappa o\iota \nu .}=.....\frac{m}{s}\]

  3. Το μέτρο της αρχικής ορμής είναι: \[p^{\alpha \rho \chi }=m_{1}\mathrm{v}_{_{1}}^{\alpha \rho \chi }\Rightarrow p^{\alpha \rho \chi }=.......kg\cdot \frac{m}{s}\]

  4. To μέτρο της τελικής ορμής του συστήματος είναι: \[p^{\tau \epsilon \lambda}=(m_{1}+m_{2})\mathrm{v}^{\kappa o\iota \nu . }\Rightarrow p^{\tau \epsilon \lambda }=.......kg\cdot \frac{m}{s}\]

  5. Παρατηρώ ότι η Αρχή διατήρησης της ορμής ..........................

  6. Η αρχική κινητική ενέργεια του συστήματος είναι: \[K^{\alpha \rho \chi }=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{(\alpha \rho \chi) })^2\Rightarrow K^{\alpha \rho \chi }=....... Joule\]

  7. Η τελική κινητική ενέργεια του συστήματος είναι: \[K^{\tau \epsilon \lambda }=\frac{1}{2}(m_{1}+m_{2})(\mathrm{v}^{(\kappa o\iota \nu .) })^2\Rightarrow K^{\tau \epsilon \lambda }=....... Joule\]

  8. Από την Αρχή Διατήρησης της Ενέργειας έχω: \(K^{\alpha \rho \chi }=K^{\tau \epsilon \lambda }+Q \). To ποσό της αρχικής ενέργειας που άλλαξε μορφή είναι: \[Q=K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }\Rightarrow Q=....... Joule\]

  9. Το ποσοστό της αρχικής ενέργειας που άλλαξε μορφή είναι: \[X=\frac{|K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }|}{K^{\alpha \rho \chi }}\cdot 100\%=\frac{Q}{K^{\alpha \rho \chi }}\cdot 100\%\Rightarrow X=.......\%\]

Πειραματικό μέρος B΄: Ελαστικές κρούσεις

  1. Οι μάζες των αμαξιδίων είναι: \(\mathrm{m_{1}=.....10^{-3}kg}\), \(\mathrm{m_{2}=.....10^{-3}kg}\).

  2. Τα μέτρα των ταχυτήτων είναι:

    \(\mathrm{v}_{_{1}}^{\alpha \rho \chi }=.....\frac{m}{s}\),   \(\mathrm{v}_{_{2}}^{\alpha \rho \chi }=.....\frac{m}{s}\)

    \(\mathrm{v}_{_{1}}^{\tau \epsilon \lambda }=.....\frac{m}{s}\),   \(\mathrm{v}_{_{2}}^{\tau \epsilon \lambda }=.....\frac{m}{s}\).


  3. Το μέτρο της αρχικής ορμής είναι: \[p^{\alpha \rho \chi }=m_{1}\mathrm{v}_{_{1}}^{\alpha \rho \chi }\Rightarrow p^{\alpha \rho \chi }=.......kg\cdot \frac{m}{s}\]

  4. To μέτρο της τελικής ορμής του συστήματος είναι: \[p^{\tau \epsilon \lambda}=-m_{1}\mathrm{v}_{_{1}}^{\tau \epsilon \lambda }+m_{2}\mathrm{v}_{_{2}}^{\tau \epsilon \lambda }\Rightarrow p^{\tau \epsilon \lambda }=.......kg\cdot \frac{m}{s}\]

  5. Παρατηρώ ότι η Αρχή διατήρησης της ορμής ....................

  6. Η αρχική κινητική ενέργεια του συστήματος είναι: \[K^{\alpha \rho \chi }=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{(\alpha \rho \chi) })^2\Rightarrow K^{\alpha \rho \chi }=....... Joule\]

  7. Η τελική κινητική ενέργεια του συστήματος είναι: \[K^{\tau \epsilon \lambda }=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{\tau \epsilon \lambda })^2+\frac{1}{2}m_{2}(\mathrm{v}_{_{2}}^{\tau \epsilon \lambda })^2\Rightarrow K^{\tau \epsilon \lambda }=....... Joule\]

  8. Από την Αρχή Διατήρησης της Ενέργειας, θα πρέπει \(K^{\alpha \rho \chi }=K^{\tau \epsilon \lambda }\) , αν η κρούση είναι ελαστική. Είναι;

  9. Αν \(K^{\alpha \rho \chi }\neq K^{\tau \epsilon \lambda }\), υπολογίζω το ποσό της αρχικής ενέργειας που άλλαξε μορφή: \[K^{\alpha \rho \chi }=K^{\tau \epsilon \lambda }+Q\Rightarrow Q=K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }\Rightarrow Q=....... Joule\]

  10. Υπολογίζω το ποσοστό της αρχικής κινητικής ενέργειας που, τελικά, έγινε θερμότητα: \[X=\frac{|K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }|}{K^{\alpha \rho \chi }}\cdot 100\%=\frac{Q}{K^{\alpha \rho \chi }}\cdot 100\%\Rightarrow X=.......\%\]

  11. Συμπεράσματα.


Παρουσίαση της άσκησης 8
Βίντεο 8.2 Παρουσίαση της άσκησης 8.

pdf: Παρουσίαση της άσκησης 8

ΚΡΙΤΗΡΙΑ ΑΞΙΟΛΟΓΗΣΗΣ

    Κριτήριο Αξιολόγησης 1:
  1. Με τη βοήθεια της εικόνας να βρεις την ταχύτητα του κινούμενου αμαξιδίου πριν την κρούση.

    2. Απάντηση

    Σύμφωνα με την εικόνα, η ταχύτητα του κινούμενου αμαξιδίου πριν την κρούση είναι 0,609 m/s.


  2. Με γνωστά: τις μάζες των αμαξιδίων m1=245 g και m2=735 g, τις ταχύτητές τους πριν την κρούση \(\mathrm{v}_{_{1}}^{\alpha \rho \chi }=0,43 m/s \) και \(\mathrm{v}_{_{2}}^{\alpha \rho \chi }=0\), τις ταχύτητές τους μετά την κρούση \(\mathrm{v}_{_{1}}^{\tau \epsilon \lambda }=10,75 cm/s \) και \(\mathrm{v}_{_{2}}^{\tau \epsilon \lambda }=10,75 cm/s \), να βρεθούν:
    1. η ορμή πριν την κρούση στο SI,
    2. η ορμή μετά την κρούση στο SI,
    3. η κινητική ενέργεια μετά την κρούση στο SI.

    Απάντηση

    1. \(p^{\alpha \rho \chi }=m_{1}\mathrm{v}_{_{1}}^{\alpha \rho \chi }+0=0,245kg\cdot 0,43\frac{m}{s}=0,105\quad kg\cdot\frac{m}{s} \)

    2. \(p^{\tau \epsilon \lambda }=m_{1}\mathrm{v}_{_{1}}^{\tau \epsilon \lambda }+m_{2}\mathrm{v}_{_{2}}^{\tau \epsilon \lambda }=0,245kg\cdot 0,1075\frac{m}{s}+0,735kg\cdot 0,1075\frac{m}{s}\) \[p^{\tau \epsilon \lambda }=0,105\quad kg\cdot\frac{m}{s}\]
    3. \(K=\frac{1}{2}m_{1}(\mathrm{v}_{_{1}}^{\tau \epsilon \lambda })^2+\frac{1}{2}m_{2}(\mathrm{v}_{_{2}}^{\tau \epsilon \lambda })^2=\frac{1}{2}\cdot 0,245kg\cdot (0,1075 \frac{m}{s})^2+0,735kg\cdot (0,1075 \frac{m}{s})^2\) \[K=5,66\cdot 10^{-3}Joule\]

  3. Εάν η αρχική κινητική ενέργεια είναι 0,023 Joule και η τελική 0,014 Joule, να βρεθεί:
    1. το ποσό της αρχικής ενέργειας που άλλαξε μορφή,
    2. το ποσοστό της αρχικής ενέργειας που άλλαξε μορφή.

    Απάντηση

    1. \(Q=K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }=0,023Joule-0,014Joule=0,009Joule\)

    2. \(X=\frac{K^{\alpha \rho \chi }-K^{\tau \epsilon \lambda }}{K^{\alpha \rho \chi }}\cdot 100=\frac{0,023J-0,014J}{0,023J}\cdot 100=39\%\)


  4. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος
    1. Στην ελαστική κρούση, αν m1=m2, τα κινητά ανταλλάσουν ταχύτητες.
      2. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    2. Στην πλαστική κρούση η ορμή διατηρείται.
      3. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    3. Στην πλαστική κρούση η κινητική ενέργεια διατηρείται.
      4. Σωστό Λάθος επιλογή. Η μηχανική ενέργεια διατηρείται. Λάθος Σωστή επιλογή. Η μηχανική ενέργεια διατηρείται.

Βιβλιογραφία:
  • Young, H. D. (1994). Πανεπιστημιακή Φυσική τόμ.Ι. (παράγραφοι 8.1-8.5, σ. 198-210). Αθήνα: Παπαζήση.