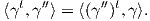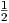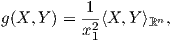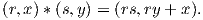Κεφάλαιο 9
Η γεωμετρία μιας ομάδας Lie
Σύνοψη
Θα μελετήσουμε αριστερά αναλλοίωτες και αμφιαναλλοίωτες μετρικές Riemann σε μια ομάδα Lie. Θα
παρουσιάσουμε τύπους για τη συνοχή Levi-Civita, την καμπυλότητα τομής, την καμπυλότητα Ricci και τη βαθμωτή
καμπυλότητα για μια συμπαγή ομάδα Lie. Θα ταξινομήσουμε τις αριστερά αναλλοίωτες μετρικές στην SU(2) S3
και θα μελετήσουμε τη γεωμετρία αυτής. Οι αναφορές μας είναι τα βιβλία [1], [2], [3], [4] και [6]. Το βιβλίο [8] και η
εργασία [9] είναι αρκετά αυξημένης δυσκολίας.
S3
και θα μελετήσουμε τη γεωμετρία αυτής. Οι αναφορές μας είναι τα βιβλία [1], [2], [3], [4] και [6]. Το βιβλίο [8] και η
εργασία [9] είναι αρκετά αυξημένης δυσκολίας.
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Εισαγωγή στις Πολλαπλότητες, Εισαγωγή στις Ομάδες Lie, Γραμμική Άλγεβρα.
΄Ενα εσωτερικό γινόμενο στον εφαπτόμενο χώρο μιας ομάδας Lie ορίζει μια μετρική Riemann η οποία είναι
αριστερά αναλλοίωτη, δηλαδή οι αριστερές μεταφορές είναι ισομετρίες. Η μελέτη της γεωμετρίας Riemann μιας
τέτοιας μετρικής είναι σημαντική, αλλά διάφοροι τύποι για τη συνοχή Levi-Civita, καμπυλότητα, κ.λπ., είναι κάπως
περίπλοκοι (βλ. για παράδειγμα [3], [9]). Μια συμπαγής όμως ομάδα Lie επιδέχεται πάντα μια μετρική Riemann, η
οποία να είναι αριστερά και δεξιά αναλλοίωτη (αμφιαναλλοίωτη, δες και τον Ορισμό 9.2) και τότε οι τύποι των
καμπυλοτήτων απλουστεύονται δραστικά.
9.1 Αριστερά αναλλοίωτες μετρικές
Ορισμός 9.1: Μια μετρική Riemann g σε μια ομάδα Lie G καλείται αριστερά αναλλοίωτη (left-invariant),
εάν οι αριστερές μεταφορές Lα : G → G είναι ισομετρίες, για κάθε α ∈ G. Συγκεκριμένα, ισχύει
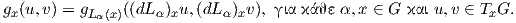
Ανάλογα, μια μετρική Riemann θα καλείται δεξιά αναλλοίωτη αν οι δεξιές μεταφορές Rα : G → G είναι ισομετρίες.
Επειδή κάθε σημείο α ∈ G μπορεί να μεταφερθεί στο ουδέτερο σημείο e ∈ G μέσω των αριστερών ή δεξιών
μεταφορών, ο εφαπτόμενος χώρος TαG είναι ισόμορφος με τον TeG. Συνεπώς, η συνθήκη για να είναι η μετρική g
αριστερά αναλλοίωτη γράφεται ως
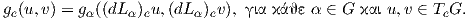
Συνήθως παραλείπουμε το ουδέτερο στοιχείο και γράφουμε απλά g(u,υ) = gα(dLα(u),dLα(υ)). ΄Ετσι μια
αριστερά αναλλοίωτη μετρική στην G είναι ένα εσωτερικό γινόμενο στην άλγεβρα Lie 𝔤. Συγκεκριμένα, ισχύει η
εξής σημαντική πρόταση:
Πρόταση 9.1: ϒπάρχει μια 1 - 1 αντιστοιχία μεταξύ των αριστερά αναλλοίωτων μετρικών σε μια ομάδα
Lie G και εσωτερικών γινομένων στην άλγεβρα Lie 𝔤 της G (ή στον εφαπτόμενο χώρο TeG, μέσω του
κανονικού ισομορφισμού 𝔤 ∋ X → Xe ∈ TeG).
Απόδειξη. ΄Εστω g μια αριστερά αναλλοίωτη μετρική στην G και X,Y ∈ 𝔤. Τότε η συνάρτηση
g(X,Y ) : G → ℝ, α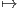 g(X,Y )(α) ≡ gα(Xα,Y α) είναι σταθερή στην G. Πράγματι, για κάθε α ∈ G και επειδή τα
διανυσματικά πεδία X,Y είναι αριστερά αναλλοίωτα, θα έχουμε ότι
g(X,Y )(α) ≡ gα(Xα,Y α) είναι σταθερή στην G. Πράγματι, για κάθε α ∈ G και επειδή τα
διανυσματικά πεδία X,Y είναι αριστερά αναλλοίωτα, θα έχουμε ότι
όπου η τρίτη ισότητα προκύπτει από το γεγονός ότι η μετρική είναι αριστερά αναλλοίωτη. ΄Αρα επειδή
g(X,Y )(α) = ge(X,Y ), η συνάρτηση
g(X,Y ) ορίζει ένα εσωτερικό γινόμενο
ge( , ) ≡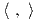 e
e στην
𝔤.
Αντίστροφα, έστω
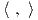 e
e ένα εσωτερικό γινόμενο στην
𝔤. Τότε η μετρική που ορίζεται ως
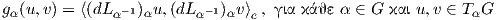
είναι μια αριστερά αναλλοίωτη μετρική στην G. Αρκεί να δείξουμε ότι για κάθε α,g ∈ G και u,υ ∈ TαG ισχύει
gα(u,υ) = gLg(α)((dLg)αu,(dLg)αυ). Πράγματι, είναι
▄
Ορισμός 9.2: Μια μετρική Riemann σε μια ομάδα Lie η οποία είναι ταυτόχρονα αριστερά και δεξιά
αναλλοίωτη ονομάζεται amfianallo�wth (bi-invariant).
Ορισμός 9.3: ΄Ενα εσωτερικό γινόμενο ⟨ , ⟩ στην άλγεβρα Lie 𝔤 μιας ομάδας Lie G ονομάζεται
Ad-αναλλοίωτο εάν ισχύει η σχέση
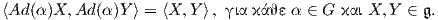
Για τις αμφιαναλλοίωτες μετρικές ισχύει ο εξής χαρακτηρισμός:
Πρόταση 9.2: ϒπάρχει μια 1 - 1 αντιστοιχία μεταξύ των αμφιαναλλοίωτων μετρικών σε μια ομάδα Lie
G και Ad-αναλλοίωτων εσωτερικών γινομένων στην άλγεβρα Lie 𝔤 της G. Επιπλέον, η συνθήκη του
Ad-αναλλοίωτου είναι ισοδύναμη με τη σχέση ![⟨[X,Y ],Z⟩](02_chapter_0910x.png) =
= ![⟨X, [Y,Z ]⟩](02_chapter_0911x.png) .
.
Απόδειξη. Θυμίζουμε ότι η συζυγής αναπαράσταση Ad : G → Aut(𝔤) της ομάδας G έχει τύπο Ad(α) = (dIα)e,
όπου Iα : G → G,x αxα-1 είναι ο εσωτερικός αυτομορφισμός της G, για τον οποίο ισχύει Iα = Lα ∘ Rα-1.
΄Εστω g μια αμφιαναλλοίωτη μετρική στην G. Τότε, επειδή η μετρική θα είναι ταυτόχρονα αριστερά και δεξιά
αναλλοίωτη, από την Πρόταση 9.1 η απεικόνιση g(X,Y ) : G → ℝ ορίζει ένα εσωτερικό γινόμενο
ge(X,Y ) =
αxα-1 είναι ο εσωτερικός αυτομορφισμός της G, για τον οποίο ισχύει Iα = Lα ∘ Rα-1.
΄Εστω g μια αμφιαναλλοίωτη μετρική στην G. Τότε, επειδή η μετρική θα είναι ταυτόχρονα αριστερά και δεξιά
αναλλοίωτη, από την Πρόταση 9.1 η απεικόνιση g(X,Y ) : G → ℝ ορίζει ένα εσωτερικό γινόμενο
ge(X,Y ) = 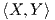 e στην 𝔤. Θα δείξουμε ότι αυτό είναι Ad-αναλλοίωτο. Πράγματι, έστω α ∈ G και X,Y ∈ 𝔤.
Τότε είναι
e στην 𝔤. Θα δείξουμε ότι αυτό είναι Ad-αναλλοίωτο. Πράγματι, έστω α ∈ G και X,Y ∈ 𝔤.
Τότε είναι
Τέλος, θα δείξουμε ότι, αν το εσωτερικό γινόμενο
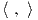
στον χώρο
𝔤 είναι
Ad-αναλλοίωτο, τότε για κάθε
X,Y,Z ∈ 𝔤 ικανοποιείται η σχέση
΄Εστω
ϕX(t) = exp(tX) η μονοπαραμετρική υποομάδα του
X ∈ 𝔤. Τότε
Στην έκτη ισότητα χρησιμοποιήσαμε το γεγονός ότι το εσωτερικό γινόμενο είναι
Ad-αναλλοίωτο. Συγκεκριμένα τη
σχέση
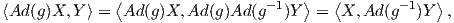
όπου g ήταν το exp(tX), για το οποίο ισχύει (exp(tX))-1 = exp(-tX). Η ισότητα (9.1) είναι ισοδύναμη με τη
σχέση ![⟨[X, Y],Z ⟩](02_chapter_0919x.png) =
= ![⟨X, [Y,Z]⟩](02_chapter_0920x.png) . Το αντίστροφο αφήνεται ως άσκηση. ▄
. Το αντίστροφο αφήνεται ως άσκηση. ▄
Για την περίπτωση μιας συμπαγούς ομάδας Lie και λόγω του Θεώρημα 8.4, ισχύει το εξής:
Θεώρημα 9.1: Κάθε συμπαγής ομάδα Lie επιδέχεται μια αμφιαναλλοίωτη μετρική.
Η μορφή Killing B μιας ομάδας Lie G είναι Ad-αναλλοίωτη (Πρόταση 8.6). Επίσης, όταν η G είναι συμπαγής
και ημιαπλή, τότε η B είναι αρνητικά ορισμένη (Θεώρημα 8.10). Κατά συνέπεια, η συμμετρική μορφή -B ορίζει ένα
εσωτερικό γινόμενο στην άλγεβρα Lie 𝔤 της G, άρα από την προηγούμενη πρόταση αν η G είναι συμπαγής και
ημιαπλή, τότε η -B ορίζει μια αμφιαναλλοίωτη μετρική σε αυτήν.
Παράδειγμα. Η ομάδα Lie SU(2) είναι συμπαγής και ημιαπλή και έχει μορφή Killing B(X,Y ) = 4trXY. Επομένως,
για κάθε X,Y ∈ 𝔰𝔲(2) το εσωτερικό γινόμενο 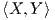 = -B(X,Y ) = -4trXY , ορίζει μια αμφιαναλλοίωτη
μετρική στην SU(2).
= -B(X,Y ) = -4trXY , ορίζει μια αμφιαναλλοίωτη
μετρική στην SU(2).
9.1.1 Αριστερά αναλλοίωτες μετρικές στην SU(2)
Η περιγραφή όλων των αριστερά αναλλοίωτων μετρικών σε μια ομάδα Lie είναι γενικά ένα δύσκολο πρόβλημα,
επειδή λόγω της Πρότασης 9.1 αυτό ανάγεται στην εύρεση όλων των εσωτερικών γινομένων σε έναν διανυσματικό
χώρο πεπερασμένης διάστασης. Στην εργασία [7] έχουν ταξινομηθεί όλες οι αριστερά αναλλοίωτες μετρικές στις
απλά συνεκτικές ομάδες Lie διάστασης 3.
Εδώ θα δείξουμε ότι όλες οι αριστερά αναλλοίωτες μετρικές στην ομάδα Lie SU(2) είναι ισοδύναμες ως προς
έναν αυτομορφισμό της 𝔰𝔲(2) με τη διαγώνια μετρική. Λέγοντας διαγώνια μετρική εννοούμε τη μετρική, της
οποίας ο πίνακας ως προς μια ορθοκανονική βάση είναι διαγώνιος. Η ομάδα Lie SU(2) είναι αμφιδιαφορική με τη
σφαίρα S3. Συνεπώς, ο καθορισμός όλων των αριστερά αναλλοίωτων μετρικών σε αυτήν μάς επιτρέπει να
περιγράψουμε πολλές γεωμετρίες της σφαίρας, πέραν αυτής που ορίζεται από την κανονική μετρική (δηλαδή αυτής
που επάγεται από τον εγκλεισμό S3 ⊂ ℝ4).
Αρχικά θα προσδιορίσουμε την ομάδα των αυτομορφισμών Aut(𝔰𝔲(2)) της 𝔰𝔲(2). Θυμίζουμε ότι το σύνολο των
αυτομορφισμών ενός διανυσματικού χώρου είναι ομάδα Lie.
Πρόταση 9.3: Η ομάδα Lie Aut(𝔰𝔲(2))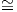 Aut(𝔰𝔬(3)) είναι ισόμορφη με την SO(3).
Aut(𝔰𝔬(3)) είναι ισόμορφη με την SO(3).
Απόδειξη. Η άλγεβρα Lie της ομάδας SO(3) είναι το σύνολο όλων των αντισυμμετρικών πινάκων, δηλαδή
Με απλό υπολογισμό βρίσκουμε ότι
![[X1, X2] = X3, [X3, X1 ] = X2, [X3,X2 ] = - X1.](02_chapter_0924x.png)
Θεωρούμε έναν αυτομορφισμό ϕ ∈ Aut(𝔰𝔬(3)) και υπολογίζουμε τον πίνακα αυτού ως προς τη βάση
{X1,X2,X3}. Στόχος μας είναι να δείξουμε ότι ο συγκεκριμένος πίνακας θα ανήκει στην ομάδα SO(3). ΄Εχουμε
Επομένως, ο πίνακας της απεικόνισης
ϕ : 𝔰𝔬(3) → 𝔰𝔬(3) θα είναι
![( )
α11 α12 α13
[ϕ] = |( α21 α22 α23 |) .
α31 α32 α33](02_chapter_0926x.png)
Επειδή ϕ ∈ Aut(𝔰𝔬(3)), θα ισχύει ότι ϕ([Xi,Xj]) = [ϕ(Xi),ϕ(Xj)]. Επομένως, θα πρέπει
άρα από την παραπάνω ισότητα θα είναι
όπου
[ϕ(i|j)] είναι ο πίνακας που προκύπτει διαγράφοντας την
i-γραμμή και την
j-στήλη. Με παρόμοιους
υπολογισμούς θα βρούμε ότι
![αij = (- 1)i+jdet[ϕ(i|j)] ≡ Aij, για κάθε i,j = 1,2,3.](02_chapter_0929x.png)
Επομένως, ο πίνακας [ϕ] θα έχει την εξής μορφή:
![( )
A11 A12 A13
[ϕ] = |( A21 A22 A23 |)
A31 A32 A33](02_chapter_0930x.png)
Στο σημείο αυτό θυμίζουμε από τη γραμμική άλγεβρα ότι, αν A ∈ Mn(K), όπου K ∈{ℝ, ℂ}, για τον οποίο
ισχύει detA≠0, τότε ο αντίστροφός του δίνεται από την σχέση A-1 = 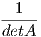 adjA. Τα στοιχεία του
προσαρτημένου πίνακα adjA δίνονται από τη σχέση Aij = (-1)i+jdetA(i|j) και αυτός είναι ίσος
με
adjA. Τα στοιχεία του
προσαρτημένου πίνακα adjA δίνονται από τη σχέση Aij = (-1)i+jdetA(i|j) και αυτός είναι ίσος
με
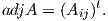
Με βάση αυτό έχουμε ότι adj[ϕ] = [ϕ]t, οπότε
![t - 1
[ϕ ][ϕ] = [ϕ]adj[ϕ] = [ϕ][ϕ ] det[ϕ] = I3det[ϕ].](02_chapter_0933x.png)
Παίρνοντας την ορίζουσα και στα δύο μέλη της παραπάνω ισότητας προκύπτει ότι
΄Αρα τελικά παίρνουμε ότι
![[ϕ][ϕ]t = I3 και det[ϕ] = 1,](02_chapter_0935x.png)
επομένως ο πίνακας της απεικόνισης ϕ : 𝔰𝔬(3) → 𝔰𝔬(3) ανήκει στην ομάδα SO(3). Δηλαδή αποδείξαμε
ότι
![ϕ ∈ Aut(𝔰𝔬(3)) αν και μόνο αν [ϕ ] ∈ SO (3).](02_chapter_0936x.png)
▄
΄Εστω G μια ομάδα Lie και 𝔤 η αντίστοιχη άλγεβρα Lie. Συμβολίζουμε με 𝔐 τον διανυσματικό χώρο όλων των
εσωτερικών γινομένων στην 𝔤 (αυτός έχει διάσταση n(n + 1)∕2) και ορίζουμε μια σχέση ισοδυναμίας ῾῾~᾿᾿ στον 𝔐
ως εξής:
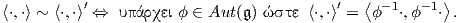
Χρησιμοποιώντας την 1 - 1 αντιστοιχία μεταξύ εσωτερικών γινομένων και αριστερά αναλλοίωτων μετρικών στην
ομάδα G, δύο αριστερά αναλλοίωτες μετρικές g,g′ θα λέγονται isod�namec wc proc �nan automorfism� thc 𝔤, αν
υπάρχει θ ∈ Aut(𝔤), έτσι ώστε
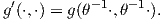
Αν θεωρήσουμε μια βάση {X1,X2,…,Xn} του χώρου 𝔤, τότε η προηγούμενη σχέση γράφεται με τη μορφή
πινάκων ως
![1Αν [g] είναι ο πίνακας της μετρικής τότε για κάθε X = ∑ αiXi,Y = ∑ βjXj ∈ 𝔤 θα ε�
[g′] = [θ-1]t[g][θ- 1]1[X ]t =(α1,α2,...,αn)t και [Y]= (β1,β2,...,βn). ,](02_chapter_0939x.png)
όπου [g′] = g′(Xi,Xj) = gij′, [g] = g(Xi,Xj) = gij οι πίνακες των μετρικών και [θ-1] ο πίνακας της απεικόνισης
θ-1 : 𝔤 → 𝔤 ως προς τη βάση {X1,X2,…,Xn}.
Με βάση τα προηγούμενα είμαστε σε θέση να αποδείξουμε ότι όλες οι αριστερά αναλλοίωτες μετρικές στην
ομάδα Lie SU(2) είναι ισοδύναμες ως προς έναν αυτομορφισμό με τη διαγώνια μετρική. Επειδή η διάσταση της
SU(2) είναι 3, αυτό σημαίνει ότι δεν θα εξαρτώνται από 3(3 + 1)∕2 = 6 παραμέτρους, αλλά μόνο από
3.
Θεώρημα 9.2: Κάθε αριστερά αναλλοίωτη μετρική στην ομάδα Lie SU(2) είναι ισοδύναμη ως προς
αυτομορφισμό, με τη μετρική της οποίας ο πίνακας ως προς μια ορθοκανονική βάση δίνεται ως
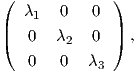
όπου λ1 ≥ λ2 ≥ λ3 > 0.
Απόδειξη. ΄Εστω g μια αριστερά αναλλοίωτη μετρική της SU(2). Θεωρούμε μια ορθοκανονική βάση
B = {X1,X2,X3} της 𝔰𝔲(2) και συμβολίζουμε με [g] = (gij) τον πίνακα της μετρικής g ως προς την B, δηλαδή
g(Xi,Xj) = gij. Ο πίνακας [g] είναι συμμετρικός και θετικά ορισμένος, οπότε υπάρχει ορθογώνιος πίνακας
P ∈ O(3), τέτοιος ώστε
όπου τα
λ1,λ2 και
λ3 είναι θετικοί αριθμοί, επειδή ο πίνακας
[g] είναι θετικά ορισμένος. Θέλουμε να δείξουμε ότι η
μετρική
g είναι ισοδύναμη ως προς έναν αυτομορφισμό της
𝔰𝔲(2) με τη διαγώνια μετρική
g′ της οποίας ο πίνακας
είναι ο
[g′]. Δηλαδή
![g ~ g′ ⇔ υπάρχει ϕ ∈ Aut (𝔰𝔲(2)) ~= SO (3) τέτοιος ώσ τε [g′] = [ϕ ]t[g][ϕ].](02_chapter_0942x.png)
Μέχρι στιγμής έχουμε ότι [g′] = Pt[g]P και P ∈ O(3). Εάν P ∈ SO(3), η απόδειξη
τελείωσε. Εάν P ∈ O(3) \ SO(3), μπορούμε να τον γράψουμε ως P = Qσ, όπου Q ∈ SO(3) και
σ = diag(-1,1,1).
Παρατηρούμε ότι για τον διαγώνιο πίνακα σ ισχύει ότι σ-1 = σ και σt = σ, οπότε θα έχουμε
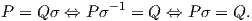
΄Αρα θα είναι
Από την παραπάνω ισότητα έχουμε ότι
Qt[g]Q = [g′], όπου
Q ∈ SO(3) Aut(𝔰𝔲(2))
Aut(𝔰𝔲(2)). Επομένως, η μετρική
g
είναι ισοδύναμη ως προς έναν αυτομορφισμό με τη διαγώνια μετρική
g′. Τέλος, επειδή οι πίνακες
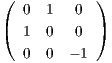 ,
,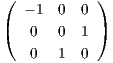
ανήκουν στην
SO(3), μπορούμε να αλλάξουμε τα διαγώνια στοιχεία
λ1,λ2 και
λ3, έτσι ώστε να έχουμε
λ1 ≥ λ2 ≥ λ3 > 0. ▄
Γενικά ισχύει το εξής, το οποίο αφήνουμε ως άσκηση:
Πρόταση 9.4: ΄Εστω G μια από τις κλασικές ομάδες Lie O(n),SO(n),U(n) ή SU(n) εφοδιασμένη με την
αριστερά αναλλοίωτη μετρική
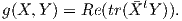
Τότε για κάθε
X ∈ 𝔤 ο τελεστής
adX : 𝔤 → 𝔤 είναι αντισυμμετρικός.
9.2 Συνοχή Levi-Civita και καμπυλότητα τομής
΄Εστω G μια ομάδα Lie εφοδιασμένη με μια αριστερά αναλλοίωτη μετρική g και έστω 𝔤 η άλγεβρα Lie της G.
Επειδή η απεικόνιση g(X,Y ) : G → ℝ είναι σταθερή για κάθε X,Y ∈ 𝔤, θα έχουμε ότι Z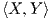 = 0 για κάθε
Z ∈ 𝔤. Συνεπώς οι τρείς πρώτοι όροι στον τύπο του Koszul (βλ. Κεφάλαιο 5) θα μηδενίζονται, άρα παίρνει τη
μορφή
= 0 για κάθε
Z ∈ 𝔤. Συνεπώς οι τρείς πρώτοι όροι στον τύπο του Koszul (βλ. Κεφάλαιο 5) θα μηδενίζονται, άρα παίρνει τη
μορφή
![2g(∇X Y, Z) = - g (X, [Y,Z])+ g(Y, [Z, X])+ g(Z, [X, Y ]).](02_chapter_0950x.png)
΄Εχουμε λοιπόν το εξής:
Πρόταση 9.5: ΄Εστω (G,g) μια ομάδα Lie εφοδιασμένη με μια αριστερά αναλλοίωτη μετρική. Τότε η συνοχή
Levi-Civita ικανοποιεί τη σχέση
![2g(∇X Y,Z ) = g(X, [Z,Y ]) + g(Y,[Z, X ]) + g(Z,[X, Y ]).](02_chapter_0951x.png)
Ισοδύναμα, η συνοχή μπορεί να εκφραστεί ως
![∇X Y = 1-([X, Y]- (adX )*Y - (adY)*X ),
2](02_chapter_0952x.png)
όπου
T* συμβολίζει τον συζυγή του τελεστή
T.
Επιπλέον, εάν η μετρική είναι αμφιαναλλοίωτη, τότε ο τελεστής adZ : 𝔤 → 𝔤 είναι αντισυμμετρικός (Πρόταση
9.2), συνεπώς η συνοχή Levi-Civita δίνεται από τη σχέση
![1
∇X Y = -[X, Y], X, Y ∈ 𝔤.
2](02_chapter_0953x.png)
Ερχόμαστε τώρα στην καμπυλότητα τομής. Θυμίζουμε ότι (βλ. Κεφάλαιο 6) ο τανυστής καμπυλότητας μιας
πολλαπλότητας Riemann δίνεται από τον τύπο
![R (X,Y )Z = - ∇ [X,Y]Z + ∇X ∇Y Z - ∇Y ∇X Z](02_chapter_0954x.png)
και η καμπυλότητα τομής ως
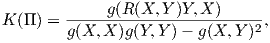 όπου
Π = span{X,Y } ένας δισδιάστατος υπόχωρος του χώρου 𝔤.
όπου
Π = span{X,Y } ένας δισδιάστατος υπόχωρος του χώρου 𝔤.
Θεωρούμε μια ορθοκανονική βάση {X1,…,Xn} της 𝔤, οπότε ο παραπάνω τύπος δίνει
Στην τέταρτη ισότητα χρησιμοποιήσαμε το γεγονός ότι η συνοχή Levi-Civita ∇ έχει μηδενική στρέψη,
δηλαδή για κάθε X,Y ∈ 𝔤 ισχύει [X,Y ] = ∇XY -∇Y X. Από την ΄Ασκηση 7 του Κεφαλαίου 5
είναι
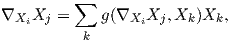 | (9.5) |
όπου η συνάρτηση g(∇XiXj,Xk) δίνεται δίνεται από το Θεώρημα 9.5. Για ευκολία στις πράξεις θέτουμε
![ckij = g([Xi,Xj ],Xk )](02_chapter_0958x.png)
και παρατηρούμε ότι cijk = -cjik και ciik = 0. Τότε ο τύπος του Koszul παίρνει τη μορφή
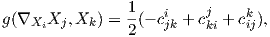
οπότε αντικαθιστώντας στην σχέση (9.5) προκύπτει ότι
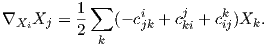
Με βάση τα παραπάνω παίρνουμε ότι
Επομένως, οι όροι στην σχέση (9.4), μετά από κάποιους υπολογισμούς, θα δίνονται ως εξής: ΄Αρα, αντικαθιστώντας στην (9.4) τις παραπάνω σχέσεις και κάνοντας πράξεις, η καμπυλότητα τομής για μια
ομάδα Lie G η οποία είναι εφοδιασμένη με μια αριστερά αναλλοίωτη μετρική δίνεται από τον τύπο:
Παράδειγμα. Θεωρούμε την ομάδα Lie SU(2) S3 με άλγεβρα Lie
S3 με άλγεβρα Lie
Θεωρούμε την αριστερά αναλλοίωτη μετρική g στην SU(2), η οποία ως προς τη βάση  X1,X2,X3
X1,X2,X3 δίνεται
ως
δίνεται
ως
![( )
| λ 0 0 |
[g] = ( 0 μ 0 ) , όπου λ ≥ μ ≥ ν > 0,
0 0 ν](02_chapter_0968x.png)
δηλαδή είναι g(X1,X1) = λ, g(X2,X2) = μ, g(X3,X3) = ν και g(Xi,Xj) = 0 για i≠j. Θέτουμε
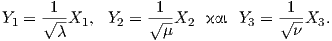
Τότε η βάση  Y 1,Y 2,Y 3
Y 1,Y 2,Y 3 είναι ορθοκανονική ως προς τη μετρική g. ϒπολογίζουμε στη συνέχεια τα γινόμενα
Lie αυτής της βάσης. Είναι
είναι ορθοκανονική ως προς τη μετρική g. ϒπολογίζουμε στη συνέχεια τα γινόμενα
Lie αυτής της βάσης. Είναι
Ανάλογα βρίσκουμε ότι
![∘ --- ∘ ---
μ λ
[Y1,Y3] = - 2 λνY2 και [Y2,Y3] = 2 μνY1.](02_chapter_0973x.png)
Οι μοναδικοί μη μηδενικοί αριθμοί cijk = g([Y i,Y j],Y k) με i,j,k = 1,2,3 είναι οι
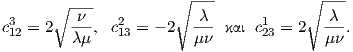
Οπότε, χρησιμοποιώντας τον τύπο (9.6) και μετά από μερικές πράξεις προκύπτει ότι η καμπυλότητα τομής της
σφαίρας S3 SU(2) είναι
SU(2) είναι
Εάν στη μετρική g θέσουμε μ = ν = 1 και για λ > 0, η σφαίρα αυτή ονομάζεται σφαίρα του
Berger.
Σε αυτή την περίπτωση η καμπυλότητα τομής της ομάδας Lie SU(2) ισούται με
Παρατηρήστε ότι για λ = 1 (δηλαδή η μετρική στην σφαίρα είναι η επαγόμενη μετρική από τον ℝ4), τότε η
καμπυλότητα είναι σταθερή και ίση με 1 (όπως αναμένεται).
Αξίζει να σημειώσουμε ότι η ομάδα Lie SU(2) είναι η μοναδική απλά συνεκτική ομάδα Lie η οποία επιδέχεται
κάποια αριστερά αναλλοίωτη μετρική, για την οποία η καμπυλότητα τομής είναι γνήσια θετική. Συγκεκριμένα,
ισχύει το εξής θεώρημα ([12]):
Θεώρημα 9.3: ΄Εστω G μια συμπαγής, συνεκτική και απλά συνεκτική ομάδα Lie. ϒποθέτουμε ότι η
G επιδέχεται μια αριστερά αναλλοίωτη μετρική με γνήσια θετική καμπυλότητα τομής. Τότε η G είναι
αμφιδιαφορική με την ομάδα Lie SU(2).
9.3 Η γεωμετρία μιας αμφιαναλλοίωτης μετρικής
Επειδή οι γενικοί τύποι για την καμπυλότητα Ricci και για τη βαθμωτή καμπυλότητα μιας αριστερά αναλλοίωτης
μετρικής γίνονται κάπως περίπλοκοι, συνήθως τους χειριζόμαστε ανάλογα με το πρόβλημα μελέτης. ΄Οταν
όμως η μετρική είναι αμφιαναλλοίωτη, τότε οι τύποι απλουστεύονται δραστικά, όπως θα δούμ στη
συνέχεια.
Πρόταση 9.6: ΄Εστω G μια ομάδα Lie εφοδιασμένη με μια αμφιαναλλοίωτη μετρική. Τότε
- (α) Η συνοχή Levi-Civita δίνεται από τη σχέση ∇XY =
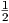 [X,Y ], για κάθε X,Y ∈ 𝔤.
[X,Y ], για κάθε X,Y ∈ 𝔤.
- (β) Οι γεωδαισιακές με αρχή το ουδέτερο στοιχείο e ∈ G είναι οι μονοπαραμετρικές υποομάδες της G.
Απόδειξη. (α) ΄Εχει αποδειχθεί στην Πρόταση 9.5.
(β) ΄Εστω αX(t) = exp(tX) η μονοπαραμετρική υποομάδα της G που παράγεται από το διανυσματικό πεδίο
X ∈ 𝔤, δηλαδή αX(0) = e και αX′(0) = X. Για να είναι η αX γεωδαισιακή, θα πρέπει ∇αX′αX′ = 0.
Πράγματι, επειδή ∇XY = 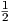 [X,Y ], είναι ∇αX′(0)αX′(0) = ∇XX =
[X,Y ], είναι ∇αX′(0)αX′(0) = ∇XX = 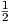 [X,X] = 0. Λόγω όμως της
μοναδικότητας, αυτές είναι όλες οι γεωδαισιακές. ▄
[X,X] = 0. Λόγω όμως της
μοναδικότητας, αυτές είναι όλες οι γεωδαισιακές. ▄
Πρόταση 9.7: ΄Εστω G μια ομάδα Lie εφοδιασμένη με μια αμφιαναλλοίωτη μετρική 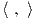 . Τότε για κάθε
X,Y,Z ∈ 𝔤 ισχύει:
. Τότε για κάθε
X,Y,Z ∈ 𝔤 ισχύει:
(α) Ο τανυστής καμπυλότητας δίνεται ως
![1
R (X, Y )Z = - -[[X, Y ],Z ].
4](02_chapter_0982x.png)
(β) Η καμπυλότητα τομής ισούται με
![K (X,Y ) = 1----⟨[X,Y-],[X,-Y-]⟩----.
4⟨X, X ⟩⟨Y,Y ⟩- ⟨X, Y⟩2](02_chapter_0983x.png)
(γ) Ο τανυστής Ricci δίνεται από τη σχέση
![∑
Ric(X, Y ) = ⟨[X, Ei],[Y,Ei]⟩,
i](02_chapter_0984x.png)
όπου {Ei} είναι μια ορθοκανονική βάση της άλγεβρας Lie 𝔤.
Απόδειξη. (α) Από προηγούμενη πρόταση έχουμε ότι ∇XY = 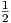 [X,Y ], οπότε ο τύπος του τανυστή καμπυλότητας
παίρνει τη μορφή
[X,Y ], οπότε ο τύπος του τανυστή καμπυλότητας
παίρνει τη μορφή
Από την ταυτότητα του
Jacobi έχουμε
οπότε προκύπτει ότι
R(X,Y )Z = -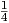 [[X,Y ],Z]
[[X,Y ],Z].
(β) Για έναν δισδιάστατο υπόχωρο
Π = span{X,Y } γνωρίζουμε ότι η καμπυλότητα τομής δίνεται από τον τύπο
K(Π) = 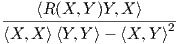 .
. Από την περίπτωση (α) έχουμε
Επειδή η μετρική είναι αμφιαναλλοίωτη, το εσωτερικό γινόμενο στον χώρο
𝔤 θα είναι
Ad-αναλλοίωτο, άρα θα
ισχύει
![⟨[[X,Y ],Y],X ⟩ = ⟨[X,Y ],[Y,X ]⟩ = - ⟨[X, Y],[X, Y ]⟩.](02_chapter_0991x.png)
Συνεπώς, θα είναι 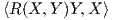 =
= 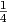
![⟨[X, Y],[X, Y ]⟩](02_chapter_0994x.png) και αντικαθιστώντας στο τύπο της καμπυλότητας θα
έχουμε
και αντικαθιστώντας στο τύπο της καμπυλότητας θα
έχουμε
![1 ⟨[X,Y ],[X, Y ]⟩
K (X,Y ) = 4---------------------2.
⟨X, X ⟩⟨Y,Y ⟩- ⟨X, Y⟩](02_chapter_0995x.png)
(γ) Για τον τανυστή Ricci θα είναι
Η τέταρτη ισότητα ισχύει, επειδή το εσωτερικό γινόμενο είναι
Ad-αναλλοίωτο. ▄
Από το (γ) της προηγούμενης πρότασης προκύπτει ότι ο τελεστής Ricci r : 𝔤 → 𝔤 δίνεται από τον
τύπο
![1-∑
r(X ) = - 4 [[X, Ei],Ei ].
i](02_chapter_0997x.png)
Πράγματι, για κάθε X,Y ∈ 𝔤 έχουμε
Πρόταση 9.8: ΄Εστω G μια συμπαγής ομάδα Lie εφοδιασμένη με μια αμφιαναλλοίωτη μετρική η οποία
προέρχεται από τη μορφή Killing της G. Τότε η βαθμωτή καμπυλότητα δίνεται ως S = 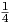 dimG.
dimG.
Απόδειξη. Γνωρίζουμε ότι η βαθμωτή καμπυλότητα είναι το ίχνος του τελεστή Ricci, οπότε, αν {Ei} είναι μια
ορθοκανονική βάση της 𝔤, τότε
▄
Θυμίζουμε ότι μια πολλαπλότητα Riemann (M,g) λέγεται Einstein, αν ο τανυστής καμπυλότητας Ricci
είναι κάποιο πολλαπλάσιο της μετρικής. Στην περίπτωση που η πολλαπλότητα είναι κάποια ομάδα
Lie G, τότε η παρακάτω πρόταση μας λέει ότι η G είναι πολλαπλότητα Einstein ως προς τη μορφή
Killing.
Πρόταση 9.9: ΄Εστω G μια συμπαγής και ημιαπλή ομάδα Lie εφοδιασμένη με μια αμφιαναλλοίωτη μετρική.
Τότε
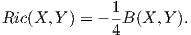
Απόδειξη. Από τον ορισμό της μορφής Killing και την Πρόταση 9.7 έχουμε ότι
▄
Παράδειγμα. Θα υπολογίσουμε την καμπυλότητα της SU(3) ως προς μια αμφιαναλλοίωτη μετρική
([11]).
Η άλγεβρα Lie της SU(3) είναι
Θεωρούμε στην SU(3) την αμφιαναλλοίωτη μετρική
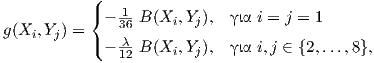
όπου B(X,Y ) = 6trXY. Επειδή η βάση {X1,X2,…,X8} δεν είναι ορθοκανονική ως προς την g,
θέτουμε
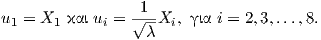
Τότε από την Πρόταση 9.7 προκύπτει ότι η καμπυλότητα τομής ισούται με
Επίσης, γνωρίζουμε από το Κεφάλαιο 6 ότι, αν {E1,…,En} είναι μια ορθοκανονική βάση του χώρου TpM, σε
κάποιο σημείο p ∈ M, τότε η καμπυλότητα Ricci ορίζεται από την καμυλότητα τομής, δηλαδή
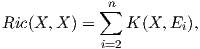
όπου X = Ei. Επομένως, η καμπυλότητα Ricci της ομάδας SU(3) θα δίνεται ως
Είναι η SU(3) μια πολλαπλότητα Einstein ως προς αυτή τη μετρική;
9.4 Ασκήσεις
1. Αποδείξτε την Πρόταση 9.4.
2. Αποδείξτε ότι μια ομάδα Lie εφοδιασμένη με μια αριστερά αναλλοίωτη μετρική έχει σταθερή βαθμωτή
καμπυλότητα.
2. Θεωρούμε την ειδική ορθογώνια ομάδα SO(n) εφοδιασμένη με τη μετρική
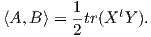
(α) Αποδείξτε ότι η παραπάνω σχέση ορίζει μια αριστερά αναλλοίωτη μετρική στην SO(n) και ότι για οποιαδήποτε
αριστερά αναλλοίωτα διανυσματικά πεδία X,Y ∈ 𝔰𝔬(n) ισχύει
![1
∇X Y = 2[X,Y ].](02_chapter_09110x.png) (β)
΄Εστω A,B,C αριστερά αναλλοίωτα διανυσματικά πεδία των οποίων η τιμή στο ουδέτερο στοιχείο I (ταυτοτικός
πίνακας) είναι
(β)
΄Εστω A,B,C αριστερά αναλλοίωτα διανυσματικά πεδία των οποίων η τιμή στο ουδέτερο στοιχείο I (ταυτοτικός
πίνακας) είναι
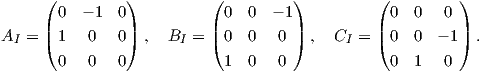 Αποδείξτε ότι το σύνολο {A,B,C} είναι μια ορθοκανονική βάση της 𝔰𝔬(3) και υπολογίστε τα διανυσματικά πεδια
∇AB,∇BC και ∇CA.
Αποδείξτε ότι το σύνολο {A,B,C} είναι μια ορθοκανονική βάση της 𝔰𝔬(3) και υπολογίστε τα διανυσματικά πεδια
∇AB,∇BC και ∇CA.
3. ΄Εστω Sol3 η τρισδιάστατη υποομάδα Lie της SL3ℝ
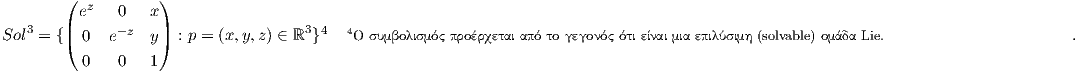 ΄Εστω
X,Y,Z ∈ 𝔤 τα διανυσματικά πεδία της Sol3 τέτοια ώστε
΄Εστω
X,Y,Z ∈ 𝔤 τα διανυσματικά πεδία της Sol3 τέτοια ώστε
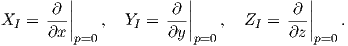 (α)
Δείξτε ότι
(α)
Δείξτε ότι
![[X,Y ] = 0, [Z,X ] = X, [Z,Y ] = - Y.](02_chapter_09114x.png) (β)
΄Εστω g η αριστερά αναλλοίωτη μετρική στην Sol3, ώστε το σύνολο {X,Y,Z} να είναι ένα ορθοκανονική βάση της
𝔤. ϒπολογίστε τα διανυσματικά πεδία ∇XY,∇XZ και ∇Y Z.
(β)
΄Εστω g η αριστερά αναλλοίωτη μετρική στην Sol3, ώστε το σύνολο {X,Y,Z} να είναι ένα ορθοκανονική βάση της
𝔤. ϒπολογίστε τα διανυσματικά πεδία ∇XY,∇XZ και ∇Y Z.
4. ΄Εστω O(n) η ορθογώνια ομάδα εφοδιασμένη με την αριστερά αναλλοίωτη μετρική g(A,B) = tr(AtB).
Αποδείξτε ότι η λεία καμπύλη γ : (-ε,ε) → O(n) είναι γεωδαισιακή εάν και μόνο εάν ισχύει
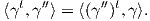
5. Θεωρούμε την ομάδα Lie S3 SU(2) εφοδιασμένη με τη μετρική g(A,B) =
SU(2) εφοδιασμένη με τη μετρική g(A,B) = 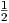 Re(tr(AtB)). Βρείτε μια
ορθοκανονική βάση του εφαπτόμενου χώρου TISU(2) και αποδείξτε ότι η πολλαπλότητα Riemann (SU(2),g) έχει
σταθερή καμπυλότητα τομής ίση με 1.
Re(tr(AtB)). Βρείτε μια
ορθοκανονική βάση του εφαπτόμενου χώρου TISU(2) και αποδείξτε ότι η πολλαπλότητα Riemann (SU(2),g) έχει
σταθερή καμπυλότητα τομής ίση με 1.
6. ΄Εστω ℍn = ℝ+ × ℝn-1 ο n-διάστατος υπερβολικός χώρος εφοδιασμένος με τη μετρική Riemann
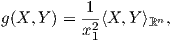 όπου
p = (x1,…,xn) ∈ ℍn. Θεωρούμε τα διανυσματικά πεδία Xk ∈ X(ℍn), k = 1,…,n με τιμή
όπου
p = (x1,…,xn) ∈ ℍn. Θεωρούμε τα διανυσματικά πεδία Xk ∈ X(ℍn), k = 1,…,n με τιμή
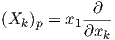 και
ορίζουμε στον ℍn την πράξη
και
ορίζουμε στον ℍn την πράξη
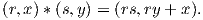 Δείξτε ότι:
Δείξτε ότι:
(α) Το ζεύγος (ℍn,*) είναι μια ομάδα Lie.
(β) Τα διανυσματικά πεδία X1,…,Xn είναι αριστερά αναλλοίωτα.
(γ) [Xk,Xl] = 0 και [X1,Xk] = Xk για k,l = 2,…,n.
(δ) Η μετρική g είναι αριστερά αναλλοίωτη.
(ε) Η πολλαπλότητα Riemann (ℍn,g) έχει σταθερή καμπυλότητα ίση με -1.
7. ϒπολογίστε την καμπυλότητα Ricci της σφαίρας του Berger. Αναζητήστε και μελετήστε την εργασία
[11].
Βιβλιογραφία
[1] A. Arvanitoyeorgos, An Introduction to Lie Groups and the Geometry of Homogeneous Spaces,
American Mathematical Society, 2003.
[2] Α. Αρβανιτογεώργος, Ομάδες Lie, Ομογενείς Χώροι και Διαφορική Γεωμετρία, Εκδόσεις
Τροχαλία, Αθήνα 1999.
[3] J. Cheeger and D.G. Ebin, Comparison Theorems in Riemannian Geometry, AMS Chelsea
Publishing Company, Providence, RI 1975.
[4] M. P. Do Carmo, Riemannian Geometry, Birkhäuser, Boston, 1992.
[5] P. M. Gadea and J. A. Oubina, Homogeneous Riemannian structures on Berger 3-spheres,
Proc. Edinburgh Math. Soc. 48 (2005) 375–387.
[6] S. Gallot, D. Hulin and J. Lafontaine, Riemannian Geometry, Springer-Verlag, New York,
1987.
[7] K. Y. Ha and J. B. Lee: Left invariant metrics and curvatures on simply connected
three-dimensional Lie groups, Math. Nachr. 282 (6) (2009) 868–898.
[8] S. Helgason, Differential Geometry, Lie Groups and Symmetric Spaces, Academic Press, New
York 1978.
[9] J. Milnor, Curvatures of left invariant metrics on Lie groups, Adv. Math. 21 (3) (1976) 293–329.
[10] P. Petersen, Riemannian Geometry, Second Edition, Springer-Verlag New York, 2006.
[11] Y-S. Pyo, H.W. Kim and J-S. Park: On Ricci curvature of left invariant metrics on SU(2),
Bull. Korean Math. Soc. 46 (2) (2009) 255–261.
[12] N. R. Wallach: Compact homogeneous Riemannian manifolds with strictly positive sectional
curvature, Ann. of Math. 96 (1972) 277-295.
 S3
και θα μελετήσουμε τη γεωμετρία αυτής. Οι αναφορές μας είναι τα βιβλία [1], [2], [3], [4] και [6]. Το βιβλίο [8] και η
εργασία [9] είναι αρκετά αυξημένης δυσκολίας.
S3
και θα μελετήσουμε τη γεωμετρία αυτής. Οι αναφορές μας είναι τα βιβλία [1], [2], [3], [4] και [6]. Το βιβλίο [8] και η
εργασία [9] είναι αρκετά αυξημένης δυσκολίας.
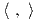
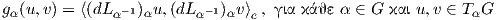
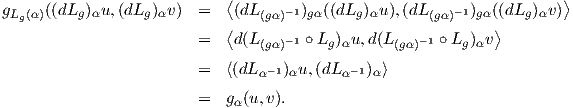
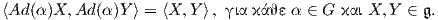
![⟨[X,Y ],Z⟩](02_chapter_0910x.png)
![⟨X, [Y,Z ]⟩](02_chapter_0911x.png)

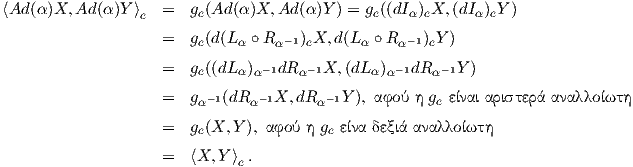
 στον χώρο
στον χώρο ![⟨[X,Y ],Z ⟩ = ⟨X, [Y,Z]⟩.](02_chapter_0916x.png)
![⟨[X, Y ],Z ⟩ = ⟨ad(X )Y, Z⟩ = ⟨((dAd )eX )Y, Z⟩
⟨ ⟩ ⟨ d ⟩
= (dAd)e(ϕ′X (0 ))Y,Z = --Ad(exp(tX ))Y |t=0,Z
dt
= -d⟨Ad (exp (tX ))Y,Z ⟩| = d-⟨Y,Ad (exp (- tX ))Z ⟩|
dt t=0 dt t=0
= ⟨Y,- ad(X)Z ⟩ = - ⟨Y,[X, Z]⟩ (9.1)](02_chapter_0917x.png)
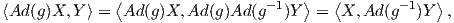
![⟨[X, Y],Z ⟩](02_chapter_0919x.png)
![⟨X, [Y,Z]⟩](02_chapter_0920x.png)
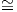
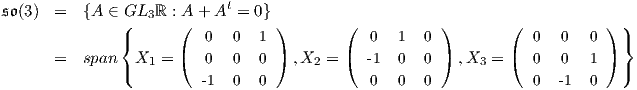
![[X1, X2] = X3, [X3, X1 ] = X2, [X3,X2 ] = - X1.](02_chapter_0924x.png)
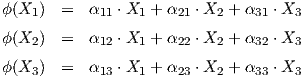
![( )
α11 α12 α13
[ϕ] = |( α21 α22 α23 |) .
α31 α32 α33](02_chapter_0926x.png)
![ϕ([X1,X2 ]) = [ϕ(X1 ),ϕ(X2)] ⇔
3 3
ϕ(X ) = [∑ α X ,∑ α X ] ⇔
3 i1 1 i2 i
3 i=1 i=1
∑
αi3Xi = [α21X2, α12X1 ]+ [α31X3, α12X1 ]+ [α11X1, α22X2 ]
i=1
+[α31X3,α22X2 ]+ [α11X1,α32X3 ]+ [α21X2,α32X3 ] ⇔
α X + α X + α X = (α α - α α )X + (α α - α α )X
13 1 23 2 33 3 21 32 31 22 1 31 12 11 32 2
+(α11α22 - α21α12)X3,](02_chapter_0927x.png)
![( )
α = α α - α α = det α21 α22 = det[ϕ(1|3)]
13 21 32 31 22 α31 α32
( )
α11 α12
α23 = α31α12 - α11α32 = - det α31 α32 = - det[ϕ(2|3)]
( )
α11 α12
α33 = α11α22 - α21α12 = det α21 α2 = det[ϕ(3|3)],](02_chapter_0928x.png)
![αij = (- 1)i+jdet[ϕ(i|j)] ≡ Aij, για κάθε i,j = 1,2,3.](02_chapter_0929x.png)
![( )
A11 A12 A13
[ϕ] = |( A21 A22 A23 |)
A31 A32 A33](02_chapter_0930x.png)
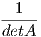
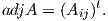
![t - 1
[ϕ ][ϕ] = [ϕ]adj[ϕ] = [ϕ][ϕ ] det[ϕ] = I3det[ϕ].](02_chapter_0933x.png)
![det([ϕ][ϕ]t) = det(I3det[ϕ]) ⇔
det[ϕ]det[ϕ]t = (det[ϕ])3 ⇔
3
det[ϕ ]det[ϕ] = (det[ϕ]) ⇔
1 = det[ϕ ]. (9.2)](02_chapter_0934x.png)
![[ϕ][ϕ]t = I3 και det[ϕ] = 1,](02_chapter_0935x.png)
![ϕ ∈ Aut(𝔰𝔬(3)) αν και μόνο αν [ϕ ] ∈ SO (3).](02_chapter_0936x.png)
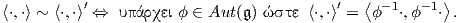
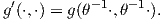
![1Αν [g] είναι ο πίνακας της μετρικής τότε για κάθε X = ∑ αiXi,Y = ∑ βjXj ∈ 𝔤 θα ε�
[g′] = [θ-1]t[g][θ- 1]1[X ]t =(α1,α2,...,αn)t και [Y]= (β1,β2,...,βn). ,](02_chapter_0939x.png)
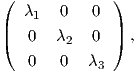
![( )
λ1 0 0
P- 1[g]P = P t[g]P = |( 0 λ2 0 |) ≡ [g′], (9.3)
0 0 λ3](02_chapter_0941x.png)
![g ~ g′ ⇔ υπάρχει ϕ ∈ Aut (𝔰𝔲(2)) ~= SO (3) τέτοιος ώσ τε [g′] = [ϕ ]t[g][ϕ].](02_chapter_0942x.png)
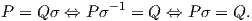
![Qt[g]Q = (Pσ)t[g ]P σ = σtPt[g]P σ = σP t[g]Pσ
( ) ( ) ( )
- 1 0 0 λ1 0 0 - 1 0 0
= |( 0 1 0 |) |( 0 λ2 0 |) |( 0 1 0 |)
0 0 1 0 0 λ 0 0 1
( ) 3
λ1 0 0
= | 0 λ 0 | = P t[g]P.
( 2 )
0 0 λ3](02_chapter_0944x.png)
 ανήκουν στην
ανήκουν στην 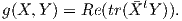
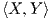
![2g(∇X Y, Z) = - g (X, [Y,Z])+ g(Y, [Z, X])+ g(Z, [X, Y ]).](02_chapter_0950x.png)
![2g(∇X Y,Z ) = g(X, [Z,Y ]) + g(Y,[Z, X ]) + g(Z,[X, Y ]).](02_chapter_0951x.png)
![∇X Y = 1-([X, Y]- (adX )*Y - (adY)*X ),
2](02_chapter_0952x.png)
![1
∇X Y = -[X, Y], X, Y ∈ 𝔤.
2](02_chapter_0953x.png)
![R (X,Y )Z = - ∇ [X,Y]Z + ∇X ∇Y Z - ∇Y ∇X Z](02_chapter_0954x.png)
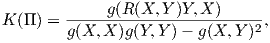
![K (Xi, Xj) = g(R (Xi,Xj)Xj, Xi)
= g(- ∇ [Xi,Xj]Xj + ∇Xi ∇Xj Xj - ∇Xj ∇XiXj, Xi)
= - g(∇ X ,X )+ g(∇ ∇ X ,X )- g(∇ ∇ X ,X )
[Xi,Xj] j i Xi Xj j i Xj Xi j i
= - g(∇ ∇X XjXj,Xi )+ g(∇ ∇X XiXj, Xi)+ g(∇Xi ∇Xj Xj,Xi )
i j
- g(∇Xj ∇XiXj, Xi). (9.4)](02_chapter_0956x.png)
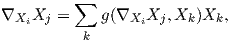
![ckij = g([Xi,Xj ],Xk )](02_chapter_0958x.png)
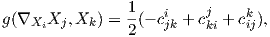
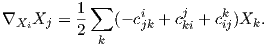
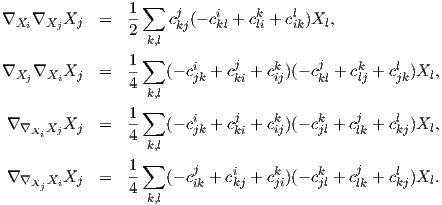
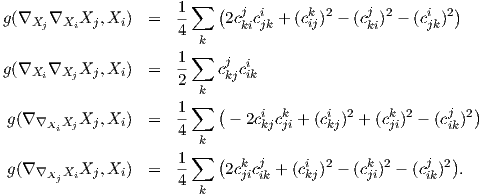
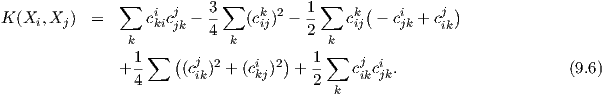

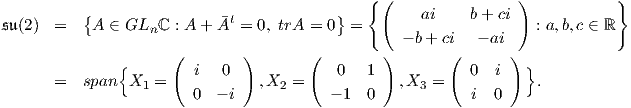
![( )
| λ 0 0 |
[g] = ( 0 μ 0 ) , όπου λ ≥ μ ≥ ν > 0,
0 0 ν](02_chapter_0968x.png)
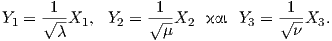
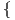
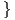
![( -1- ) ( 1--) ( -1- ) ( -1- )
[Y ,Y ] = √ λi 0 0 √μ - 0 √ μ √λi 0
1 2 0 - √1-i - √1μ- 0 - √1μ- 0 0 - √1i
( λ ) ( ) ( ) λ
0 √1λμi 0 - √iλμ- 0 √2λiμ-
= √-1-i 0 - -√-i- 0 = √2i- 0
λμ √ -- ∘ --λμ λμ
-2--- 2--ν- -ν-
= √λ-μX3 = √ λμY3 = 2 λ μY3.](02_chapter_0972x.png)
![∘ --- ∘ ---
μ λ
[Y1,Y3] = - 2 λνY2 και [Y2,Y3] = 2 μνY1.](02_chapter_0973x.png)
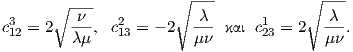
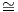
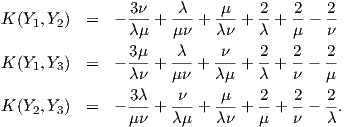
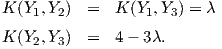
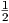
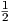
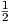
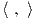 . Τότε για κάθε
. Τότε για κάθε
![1
R (X, Y )Z = - -[[X, Y ],Z ].
4](02_chapter_0982x.png)
![K (X,Y ) = 1----⟨[X,Y-],[X,-Y-]⟩----.
4⟨X, X ⟩⟨Y,Y ⟩- ⟨X, Y⟩2](02_chapter_0983x.png)
![∑
Ric(X, Y ) = ⟨[X, Ei],[Y,Ei]⟩,
i](02_chapter_0984x.png)
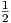
![R (X,Y )Z = - ∇ [X,Y ]Z + ∇X ∇Y Z - ∇Y ∇X Z
1 1 1
= - -[[X, Y],Z ]+ -[X,[Y,Z ]] - -[Y,[X,Z ]]
2 4( 4 )
= - 1[[X, Y],Z ]+ 1-[X, [Y, Z]]- [Y, [X, Z ]] . (9.7)
2 4](02_chapter_0986x.png)
![[[Y,Z ],X ]+ [[Z, X],Y ]+ [[X, Y],Z] = 0 ⇔
([X,[Y,Z ]]+ [Y,[Z,X ]]) = [[X,Y ],Z ] ⇔
([X,[Y,Z ]]- [Y,[X,Z ]]) = [[X,Y ],Z ],](02_chapter_0987x.png)
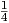
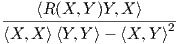
![⟨R(X, Y )Y, X⟩ = - 1⟨[[X, Y ],Y ],X ⟩. (9.8)
4](02_chapter_0990x.png)
![⟨[[X,Y ],Y],X ⟩ = ⟨[X,Y ],[Y,X ]⟩ = - ⟨[X, Y],[X, Y ]⟩.](02_chapter_0991x.png)
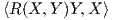
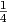
![⟨[X, Y],[X, Y ]⟩](02_chapter_0994x.png) και αντικαθιστώντας στο τύπο της καμπυλότητας θα
έχουμε
και αντικαθιστώντας στο τύπο της καμπυλότητας θα
έχουμε
![1 ⟨[X,Y ],[X, Y ]⟩
K (X,Y ) = 4---------------------2.
⟨X, X ⟩⟨Y,Y ⟩- ⟨X, Y⟩](02_chapter_0995x.png)
![∑
Ric(X, Y ) = tr{Z ↦→ R(Z,X )Y } = ⟨R (Ei,X )Y,Ei⟩
i
1∑ 1 ∑
= - -- ⟨[[Ei,X ],Y ],Ei⟩ = -- ⟨[X, Ei],[Y,Ei ]⟩.
4 i 4 i](02_chapter_0996x.png)
![1-∑
r(X ) = - 4 [[X, Ei],Ei ].
i](02_chapter_0997x.png)
![1∑ 1∑
⟨r(X ),Y ⟩ = ⟨- 4 [[X, Ei],Ei],Y⟩ = - 4 ⟨[X,Ei ],[Ei,Y]⟩
∑ i i
= 1- ⟨[X, Ei],[Y, Ei]⟩ = Ric(X, Y).
4 i](02_chapter_0998x.png)
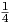
![∑ 1-∑
S = trr = ⟨r(Ei ),Ei⟩ = - 4 ⟨[[Ei,Ej],Ej],Ei ⟩
i i,j
= 1-∑ ⟨[E ,E ],[E ,E ]⟩ = 1-dimG.
4 i j i j 4
i,j](02_chapter_09100x.png)
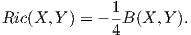
![∑ ∑
B(X, Y) = tr(adX ∘adY ) = ⟨(adX ∘ adY )Ei, Ei⟩ = ⟨[X, [Y, Ei]],Ei⟩
i i
= - ∑ ⟨[[Y,E ],X ],E ⟩ = - ∑ ⟨[Y,E ],[X, E ]⟩ = - 4 Ric(X,Y ).
i i i i
i i](02_chapter_09102x.png)
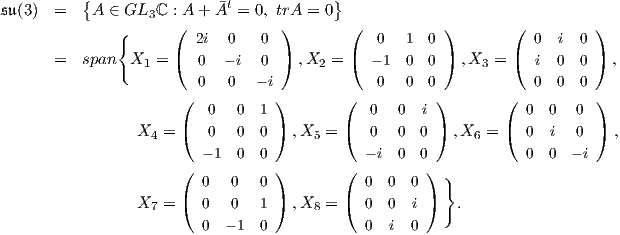
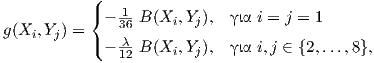
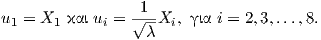
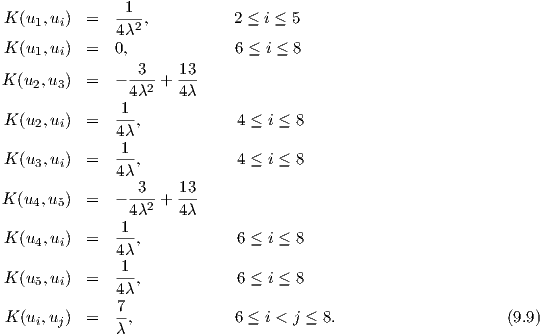
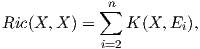
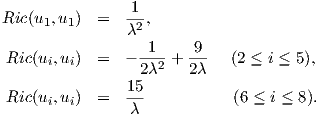
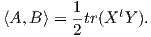
![1
∇X Y = 2[X,Y ].](02_chapter_09110x.png)
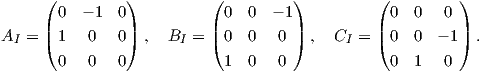
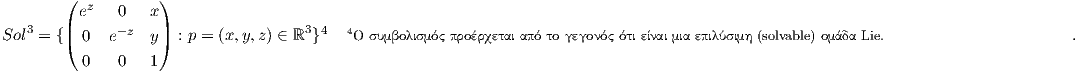
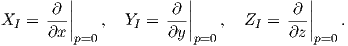
![[X,Y ] = 0, [Z,X ] = X, [Z,Y ] = - Y.](02_chapter_09114x.png)