Σύνοψη
Αρχικά κάνουμε μια σύντομη εισαγωγή σε ένα σημαντικό εργαλείο της γεωμετρίας Riemann, τα τανυστικά πεδία.
Στη συνέχεια εισάγουμε την έννοια της μετρικής Riemann σε μια λεία πολλαπλότητα. Με τον τρόπο αυτό είμαστε
σε θέση να μετράμε αποστάσεις και γωνίες. Προκειμένου να μελετήσουμε την έννοια της παραλληλίας σε μια
πολλαπλότητα Riemannn, εισάγουμε την συνοχή Levi-Civita και την έννοια του παράλληλου διανυσματικού πεδίου
κατά μήκος μιας λείας καμπύλης. Η γενίκευση της έννοιας της ευθείας σε έναν Ευκλείδειο χώρο είναι η γεωδασιακή
καμπύλη σε μια πολλαπλότηα Riemann. ΄Ενας τρόπος ορισμού των γεωδαισιακών είναι μέσω της
έννοιας του παράλληλου διανυσματικού πεδίου κατά μήκος μιας λείας καμπύλης. Η συλλογή όλων
των γεωδαισιακών σε μια περιοχή ενός σημείου με κοινό πεδιο ορισμού μας οδηγεί στον ορισμό της
εκθετικής απεικόνισης. Οι βασικές μας αναφορές είναι τα βιβλία [5], [10] και [12]. Στο ίδιο επίπεδο
δυσκολίας βρίσκονται και τα βιβλία [3], [6], [7] και [13]. Σαφώς πιο προχωρημένα είναι τα βιβλία [1] και
[2].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Συνήθεις Διαφορικές Εξισώσεις.
Ο τανυστικός λογισμός αποτελεί το πιο χρήσιμο εργαλείο της γεωμετρίας Riemann. Αναπτύχθηκε από τους Gregorio Ricci-Curbastro το διάστημα 1887-1896 και διαδόθηκε ιδιαίτερα από τον μαθητή του Tullio Levi-Civita το 1890. Αποτελεί μια ιδιαίτερα τεχνική, αλλά λειτουργική επέκταση του λογισμού των γραμμικών απεικονίσεων και του απειροστικού λογισμού σε πολλές μεταβλητές. Ο τανυστικός λογισμός, βρήκε την τέλεια εφαρμογή του στην διαφορική γεωμετρία, την γενική θεωρία της σχετικότητας του Albert Einstein, αλλά και σε άλλες επιστήμες όπως ρευστομηχανική, κ.ά.
΄Εστω M μια λεία πολλαπλότητα, F(M) ο μεταθετικός δακτύλιος των λείων συναρτήσεων στην M και X(M) το σύνολο των λείων διανυσματικών πεδίων στην M. Θυμίζουμε ότι το σύνολο X(M) αποτελεί ένα πρότυπο επί του F(M). Για κάθε θετικό ακέραιο r έστω
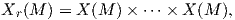
Ορισμός 5.1: ΄Ενα τανυστικό πεδίο A στην πολλαπλότητα M τύπου (r,s) είναι μια απεινόνιση A : Xs(M) → Xr(M) η οποία είναι F(M)-πολυγραμμική, δηλαδή ικανοποιεί την ιδιότητα
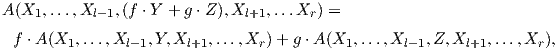
΄Ενα τανυστικό πεδίο τύπου (0,0) είναι απλώς μια συνάρτηση f ∈ F(M).
Η πιό σημαντική ιδιότητα των τανυστικών πεδίων, την οποία παραθέτουμε στη συνέχεια, είναι ότι η τιμή της συνάρτησης A(X1,…,Xs) σε ένα σημείο p ∈ M εξαρτάται μόνο από τις τιμές των διανυσματικών πεδίων X1,…,Xs στο p (και όχι από τις τιμές τους σε μια περιοχή του σημείου p).
Πρόταση 5.1: ΄Εστω A : Xs(M) → Xr(M) ένα τανυστικό πεδίο τύπου (r,s) και p ∈ M. ΄Εστω X1,…,Xs και Y 1,…,Y s λεία διανυσματικά πεδία στην πολλαπλότητα M, έτσι ώστε (Xk)p = (Y k)p για κάθε k = 1,…,s. Τότε ισχύει
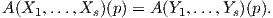
Απόδειξη. Θα αποδείξουμε το αποτέλεσμα για s = 1 και η γενικότητα προκύπτει εύκολα με επαγωγή. ΄Εστω X1 = X,Y 1 = Y και (U;x1,…,xn) ένα τοπικό σύστημα συντεταγμένων στο σημείο p. Επιλέγουμε μια συνάρτηση εξογκώματος f ∈ F(M), τέτοια ώστε f(p) = 1 και supp(f) ⊂ U. Ορίζουμε τα διανυσματικά πεδία υ1,…,υn ∈ X(M) στην πολλαπλότητα M ως εξής:
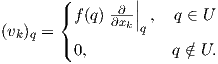
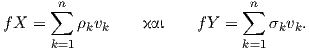
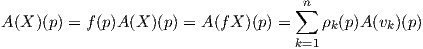
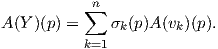
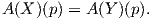
Για ένα τανυστικό πεδίο A τύπου (r,s) και για υ1,…,υp ∈ TpM, έστω
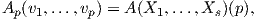
Ορισμός 5.2: Μια μετρική Riemann σε μια πολλαπλότητα M είναι ένα (συναλλοίωτο) τανυστικό πεδίο g στην M τύπου (0,2)
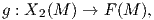
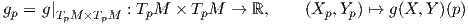
Το εσωτερικό γινόμενο gp συμβολίζεται συχνά και με ⟨ , ⟩p. Με ισοδύναμη διατύπωση, μια μετρική Riemann στην πολλαπλότητα M είναι μια απεικόνιση η οποία σε κάθε σημείο p ∈ M αντιστοιχεί ένα εσωτερικό γινόμενο gp = ⟨ , ⟩p (δηλαδή μια συμμετρική, διγραμμική και θετικά ορισμένη διγραμμική μορφή) στον εφαπτόμενο χώρο Tp, η οποία είναι λεία υπό την εξής έννοια: για κάθε ζεύγος λείων διανυσματικών πεδίων X,Y στην M η συνάρτηση
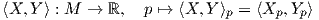
Χρησιμοποιώντας την μετρική Riemann μπορούμε να ορίσουμε το μήκος μιας λείας καμπύλης σε μια πολλαπλότητα.
Ορισμός 5.3: ΄Εστω γ : I → ℝ μια λεία καμπύλη σε μια πολλαπλότητα Riemann (M,g). Τότε το μήκος L(γ) της γ είναι το ολοκλήρωμα
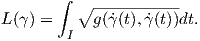
Θα δούμε τώρα την τοπική έκφραση μιας μετρικής Riemann. ΄Εστω (M,g) μια πολλαπλότητα Riemann και (U;x1,…,xn) ένα τοπικό σύστημα συντεταγμένων σε ένα σημείο p ∈ M. ΄Εστω u,υ ∈ TpM με
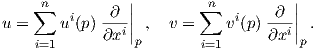
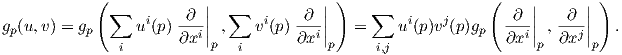
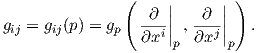
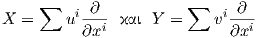
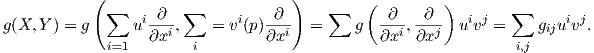
 ⟨ , ⟩p είναι λεία εάν και μόνο εάν οι συναρτήσεις gij : U → ℝ είναι λείες. Λόγω της
ισότητας dxi ⊗dxj(X,Y ) = dxi(X)dxj(Y ) = uiυj, συχνά η παραπάνω σχέση παρουσιάζεται με την την κλασική
γραφή
⟨ , ⟩p είναι λεία εάν και μόνο εάν οι συναρτήσεις gij : U → ℝ είναι λείες. Λόγω της
ισότητας dxi ⊗dxj(X,Y ) = dxi(X)dxj(Y ) = uiυj, συχνά η παραπάνω σχέση παρουσιάζεται με την την κλασική
γραφή
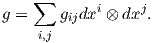
Παρατηρήστε ότι οι συναρτήσεις gij ορίζουν έναν συμμετρικό πίνακα, τον πίνακα της μετρικής
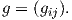
Μια πολλαπλότητα Riemann (M,g) έχει επιπλέον δομή μετρικού χώρου, όπως φαίνεται στο παρκάτω θεώρημα, για την απόδειξη του οποίου παραπέμπουμε στα βιβλία [10] και [12].
Πρόταση 5.2: ΄Εστω (M,g) μια πολλαπλότητα Riemann και p,q ∈ M. ΄Εστω Cpq το σύνολο όλων των λείων καμπυλών γ : [0,1] → M με την ιδιότητα γ(0) = p και γ(1) = q. Ορίζουμε τη συνάρτηση d : M × M → ℝ0+
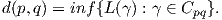
Παραδείγματα.
1. Το συνηθισμένο εσωτερικό γινόμενο
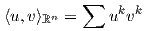
2. Εφοδιάζουμε τον διανυσματικό χώρο ℝn με την μετρική Riemann g
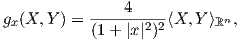
 (t,0,…,0). Τότε το μήκος
L(γ) της γ είναι
(t,0,…,0). Τότε το μήκος
L(γ) της γ είναι
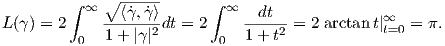
3. ΄Εστω B1n(0) η n-διάστατη ανοικτή μπάλα
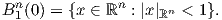
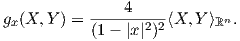
 (t,0,…,0). Τότε είναι
(t,0,…,0). Τότε είναι
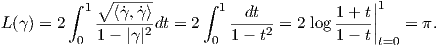
4. ΄Εστω (M1,g1) και (M2,g2) δύο πολλαπλότητες Riemann. Τότε το γινόμενο M1 × M2 εφοδιάζεται με μια μετρική Riemann ως εξής. Θεωρούμε τις προβολές πi : M1 ×M2 → Mi (i = 1,2) και για κάθε (p,q) ∈ M1 ×M2 ορίζουμε την μετρική γινόμενο
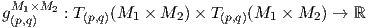
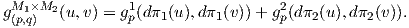
 TpM1 ⊕ TqM2, u
TpM1 ⊕ TqM2, u (dπ1(u),dπ2(u)) προκύπτει εύκολα ότι η παραπάνω
απεικόνιση είναι πράγματι μια μετρική στο γινόμενο M1 × M2.
(dπ1(u),dπ2(u)) προκύπτει εύκολα ότι η παραπάνω
απεικόνιση είναι πράγματι μια μετρική στο γινόμενο M1 × M2.
Μια μετρική Riemann σε μια λεία πολλαπλότητα επάγει μετρική Riemann σε μια υποπολλαπλότητά της, ως ακολούθως.
Ορισμός 5.4: ΄Εστω (N,h) μια πολλαπλότητα Riemann και M μια υποπολλαπλότητα της N. Το τανυστικό πεδίο
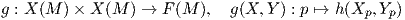
Παραδείγματα.
1. Το συνηθισμένο εσωτερικό γινόμενο ⟨ , ⟩ στον ℝn επάγει μετρικές Riemann στις εξής υποπολλαπλότητες:
(α) Στην m-διάστατη σφαίρα Sm ⊂ ℝm+1.
(β) Στην εφαπτόμενη δέσμη TSm = {(x,X) ∈ Sm × ℝm+1 : x ⊥ X}⊂ ℝ2m+2.
(γ) Στον m-διάστατο δακτύλιο Tm ⊂ ℝ2m.
2. Το σύνολο Mn(ℂ) όλων των μιγαδικών n × n πινάκων εφοδιασμένο με το Ευκλείδειο εσωτερικό γινόμενο
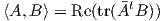
Το επόμενο βήμα είναι να αποδείξουμε ότι κάθε λεία πολλαπλότητα M επιδέχεται μια μετρική Riemann. Αυτό θα επιτευχθεί με ‘συγκόληση’ μετρικών Riemann από κάθε ανοικτό σύνολο ενός άτλαντα της M.
Θεώρημα 5.1: ΄Εστω (M,A) μια λεία πολλαπλότητα διάστασης n. Τότε η M επιδέχεται μια μετρική Riemann.
Απόδειξη. ΄Εστω A = {(Uα,φα)} η οικογένεια χαρτών του άτλαντα, η οποία καλύπτει την M. Θεωρούμε
μια διαμέριση της μονάδας {ρα} υποκείμενη του καλύμματος {Uα} (βλ. Θεώρημα 4.2). Σε κάθε χάρτη Uα
ορίζεται μια μετρική Riemann ⟨ , ⟩α λόγω του ότι το Uα είναι αμφιδιαφορικό με ένα ανοικτό υποσύνολο
του ℝn. Συγκεκριμένα, αν φα = (x1,…,xn) και X = ∑
ai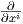 , Y = ∑
bi
, Y = ∑
bi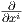 , τότε
, τότε
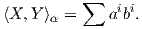
Το εσωτερικό αυτό γινόμενο είναι λείο. Πράγματι, έστω X,Y λεία διανυσματικά πεδία στην M. Τότε επειδή το άθροισμα ∑ ρα⟨ , ⟩α είναι ένα πεπερασμένο άθροισμα από λείες συναρτήσεις στο Up, θα είναι και αυτό μια λεία συνάρτηση στο Up. Επειδή το σημείο p ∈ M ήταν τυχαίο, το άθροισμα ∑ ρα⟨ , ⟩α είναι λείο στην M. ▄
Ορισμός 5.5: ΄Εστω f : (M,g) → (N,h) μια αμφιδιαφόριση μεταξύ δύο πολλαπλοτήτων Riemann. Η f ονομάζεται ισομετρία, εάν για κάθε p ∈ M και διανυσματικά πεδία X,Y ∈ X(M) ισχύει
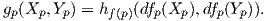
Παράδειγμα. Θεωρούμε την μοναδιαία σφαίρα Sn με την επαγόμενη μετρική Riemann ⟨ , ⟩ από τον ℝn+1. Η ορθογώνια ομάδα O(n + 1) = {A ∈ Mn+1ℝ : AAt = I} δρα στην Sn ως εξής:
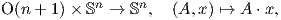
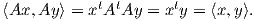
Θεώρημα 5.2: ΄Εστω 3 ≤ r ≤ ∞ και (M,g) μια πολλαπλότητα Riemann κλάσης Cr. Τότε υπάρχει μια ισομετρική εμφύτευση κλάσης Cr της (M,g) σε έναν Ευκλείδειο χώρο ℝn.
Η αρχική απόδειξη του Nash έτυχε διαφόρων απλουστεύσεων, όπως για παράδειγμα από τον M. Gunther ([8], [9]).
Το κεντρικό εργαλείο, προκειμένου να οριστούν διάφορα γεωμετρικά αντικείμενα σε μια πολλαπλότητα Riemann M, είναι αυτό της συνοχής. Επιθυμούμε να ορίσουμε παράγωγο κατά κατεύθυνση ενός λείου διανυσματικού πεδίου Y στην κατεύθυνση ενός διανύσματος Xp ∈ TpM (p ∈ M). Για τον σκοπό χρειάζεται να συγκρίνουμε τις τιμές του Y σε μια περιοχή του σημείου p. Αν q είναι ένα άλλο σημείο κοντά στο p, τότε γενικά δεν είναι δυνατόν να συγκρίνουμε τα διανύσματα Y q και Y p μέσω της διαφοράς Y q -Y p, επειδή τα αντίστοιχα διανύσματα ανήκουν σε διαφορετικούς εφαπτόμενους χώρους. Ας θυμηθούμε πώς ορίζεται η παράγωγος κατά κατεύθυνση στην περίπτωση όπου M = ℝn.
΄Εστω p ∈ ℝn, Xp ∈ Tpℝn και Y ένα λείο διανυσματικό πεδίο στον ℝn. Τότε η παράγωγος κατά κατεύθυνση του Y στην διεύθυνση Xp είναι ο αριθμός
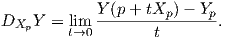
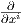 τότε
τότε
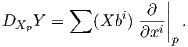
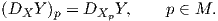
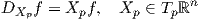
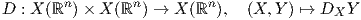
για κάθε λ,μ ∈ ℝ, f,g ∈ F(ℝn) και X,Y,Z ∈ X(ℝn).
Οι παραπάνω Ιδιότητες 1 έως 4 καθορίζουν την απεικόνιση D ως μια ομοπαραλληλική συνοχή (affine conection) στον ℝn. Εν προκειμένω αυτή ονομάζεται Ευκλείδεια συνοχή στον ℝn.
Θα γενικεύσουμε τώρα την αφινική συνοχή στον ℝn στη συνοχή Levi-Civita σε μια πολλαπλότητα Riemann.
Ορισμός 5.6: Μια ομοπαραλληλική συνοχή (affine connection) σε μια πολλαπλότητα M είναι μια ℝ-διγραμμική απεικόνιση
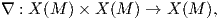
΄Ενα διανυσματικό πεδίο Y ∈ X(M) ονομάζεται παράλληλο ως προς την συνοχή ∇ εάν ισχύει ∇XY = 0 για κάθε X ∈ X(M).
Παρατήρηση. Η συνοχή ∇XY είναι τανυστής ως προς X, αλλά δεν είναι τανυστής ως προς Y.
Δοθείσης μιας ομοπαραλληλικής συνοχής ∇ σε μια πολλαπλότητα M, τίθεται το ερώτημα κατά πόσον αυτή ικανοποιεί κάποιες από τις παραπάνω ιδιότητες 1. - 5. της Ευκλείδειας συνοχής.
Ορισμός 5.7: ΄Εστω M μια λεία πολλαπλότητα και ∇ μια συνοχή στην M. Η στρέψη της συνοχής ∇ είναι η απεικόνιση
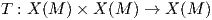
![T(X, Y) = ∇X Y - ∇Y X - [X,Y ].](02_chapter_0551x.png)
Δεν φαίνεται να υπάρχει μια επαρκώς πειστική εξήγηση γιατί η παραπάνω απεικόνιση ονομάζεται στρέψη. Το ενδιαφέρον όμως είναι ότι, αν και η συνοχή ∇XY δεν είναι F(M)-γραμμική ως προς την μεταβλητή Y , εντούτοις η στρέψη είναι F(M)-γραμμική και ως προς τις δύο μεταβλητές.
Πρόταση 5.3: ΄Εστω M μια πολλαπλότητα εφοδιασμένη με μια ομοπαραλληλική συνοχή ∇. Τότε για κάθε X,Y ∈ X(M) η στρέψη T(X,Y ) της συνοχής είναι F(M)-γραμμική ως προς X και Y (συνεπώς είναι τανυστής τύπου (1,2)).
Απόδειξη. Θα αποδείξουμε ότι για κάθε f ∈ F(M) ισχύει T(fX,Y ) = fT(X,Y ). Παρόμοια αποδεικνύεται και ότι T(X,fY ) = fT(X,Y ). Από τον ορισμό της στρέψης έχουμε ότι
![T (fX, Y) = ∇fX Y - ∇Y (f X )- [f X,Y ].](02_chapter_0552x.png)
![- f[X, Y]- f X(1)Y + (Y f)X = - f[X, Y]+ (Y f)X,](02_chapter_0553x.png)
![T (f X,Y ) = f ∇X Y - Y (f)X - f∇Y X - f[X,Y ]+ (Y f)X
= f ∇X Y - f∇Y X - f[X,Y ] = f T(X, Y).](02_chapter_0554x.png)
Μάς ενδιαφέρει τώρα να περιορίσουμε τον δυνατό αριθμό αφινικών συνοχών σε μια πολλαπλότητα Riemann.
Ορισμός 5.8: ΄Εστω (M,g) μια πολλαπλότητα Riemann. Μια συνοχή ∇ ονομάζεται συμβατή (compatible) με την μετρική g (ή μετρική συνοχή - metric connection) εάν για κάθε X,Y,Z ∈ X(M) ισχύει η σχέση
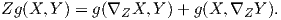
Η παραπάνω σχεσή αφορά ισότητα συναρτήσεων. Ερμηνεύεται ως τύπος παραγώγισης, γενίκευση της Ιδιότητας 5 της Ευκλείδειας συνοχής.
Ορισμός 5.9: Μια ομοπαραλληλική συνοχή σε μια πολλαπλότητα Riemann ονομάζεται συνοχή Levi-Civita,1 εάν έχει μηδενική στρέψη και είναι συμβατή με την μετρική.
Σημειώνουμε ότι η συνοχή Levi-Civita αποτελεί εσωτερική ποσότητα της πολλαπλότητας (M,g), δηλαδή εξαρτάται μόνο από την διαφορική δομή της και την μετρική g.
Ερχόμαστε τώρα στο κεντρικό αποτέλεσμα της γεωμετρίας Riemann (γνωστό και ως το ‘θαύμα’ της γεωμετρίας Riemann) το οποίο αναφέρει ότι κάθε πολλαπλότητα Riemann επιδέχεται μία και μοναδική συνοχή Levi-Civita. Θα χρειαστούμε πρώτα το εξής:
Λήμμα 5.1: ΄Ενα λείο διανυσματικό πεδίο X σε μια πολλαπλότητα Riemann (M,g) καθορίζεται πλήρως από τις τιμές της συνάρτησης g(X,Z) για κάθε Z ∈ X(M).
Απόδειξη. Αρκεί να δειχθεί ότι αν X′ ∈ X(M) τέτοιο ώστε g(X,Z) = g(X′,Z) για κάθε Z ∈ X(M), τότε X = X′. Θέτοντας Y = X - X′, αρκεί να δείξουμε ότι αν g(Y,Z) = 0 για κάθε Z ∈ X(M), τότε Y = 0. ΄Εστω Z = Y . Τότε g(Y,Y ) = 0, άρα g(Y p,Y p) = 0 για κάθε p ∈ M. Επειδή η μετρική είναι θετικά ορισμένη, προκύπτει ότι Y p = 0 για κάθε p ∈ M, συνεπώς Y = 0. ▄
Θεώρημα 5.3: (Θεμελιώδες θεώρημα της γεωμετρίας Riemann). Σε κάθε πολλαπλότητα Riemann (M,g) υπάρχει μία και μοναδική συνοχή Levi-Civita.
Απόδειξη. Αρχικά θα αποδείξουμε ότι αν μια τέτοια συνοχή υπάρχει, τότε αυτή είναι μοναδική. ΄Εστω ∇ μια συνοχή Levi-Civita στην M. Τότε λόγω του Λήμματος 5.1, προκειμένου να καθοριστεί το πεδίο ∇XY , αρκεί να γνωρίζουμε τη συνάρτηση g(∇XY,Z), για κάθε διανυσματικό πεδίο Z ∈ X(M). ΄Αρα θα προσπαθήσουμε να βρούμε έναν τύπο για την συνάρτηση g(∇XY,Z) ο οποίος θα εξαρτάται μόνο από την μετρική και πράξεις μεταξύ διανυσματικών πεδίων, όπως το γινόμενο Lie.
Θυμίζουμε ότι η συνοχή Levi-Civita ικανοποιεί τις σχέσεις
Με κυκλική εναλλαγή των X,Y,Z στην (5.2) προκύπτουν οι σχέσεις Χρησιμοποιώντας την σχέση (5.1) εκφράζουμε το πεδίο ∇Y X στην σχέση (5.3) ως προς ∇XY :
![Y g(Z,X ) = g(∇Y Z,X )+ g(Z, ∇X Y )- g(Z,[X, Y]).](02_chapter_0558x.png) | (5.5) |
Αφαιρώντας την (5.4) από την (5.2) και προσθέτοντας στο αποτέλεσμα στην (5.5), θα προκύψουν οι όροι ∇XZ -∇ZX και ∇Y Z -∇ZY , οι οποίοι λόγω της μηδενικότητας της στρέψης (5.1) ισούνται με [X,Z] και [Y,Z], όπως φαίνεται πιο κάτω:
![Xg (Y, Z) + Y g(Z,X ) - Zg(X, Y)
= 2g (∇ Y,Z) + g(Y,∇ Z - ∇ X ) + g(X,∇ Z - ∇ Y)- g(Z, [X, Y ])
X X Z Y Z
= 2g (∇X Y,Z) + g(Y,[X,Z ]) + g(X,[Y,Z ]) - g(Z,[X,Y ]).](02_chapter_0559x.png)
Παράδειγμα. Η συνοχή Levi-Civita στον ℝn εφοδιασμένου με την Ευκλείδεια μετρική, είναι η παράγωγος κατά κατεύθυνση, δηλαδή ισχύει ∇XY = DXY .
΄Εστω (M,g) μια πολλαπλότητα Riemann διάστασης n. Ας δούμε κάποιες συνέπειες, όταν εκφράσουμε τη
μετρική g και την συνοχή Levi-Civita ∇ σε ένα τοπικό σύστημα συντεταγμένων (U;φ = (x1,…,xn)) της M.
Θέτουμε Xi = 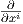 ∈ X(U). Το σύνολο {X1,…,Xn} αποτελεί ένα πλαίσιο (frame) της M, υπό την έννοια ότι για
κάθε σημείο p ∈ U το σύνολο {X1(p),…,Xn(p)} αποτελεί μια βάση του εφαπτόμενου χώρου TpM. Αν ορίσουμε
την μετρική
∈ X(U). Το σύνολο {X1,…,Xn} αποτελεί ένα πλαίσιο (frame) της M, υπό την έννοια ότι για
κάθε σημείο p ∈ U το σύνολο {X1(p),…,Xn(p)} αποτελεί μια βάση του εφαπτόμενου χώρου TpM. Αν ορίσουμε
την μετρική 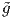 στο υποσύνολο φ(U) του ℝn ως
στο υποσύνολο φ(U) του ℝn ως
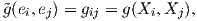
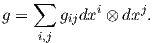
Ας εκφράζουμε τα διανυσματικά πεδία ∇XiXj συναρτήσει των πεδίων Xk,k = 1,…,n. Τότε υπάρχουν n3 το πλήθος συναρτήσεις Γijk : U → ℝ (σύμβολα του Christoffel 2) ως προς την συνοχή ∇, έτσι ώστε
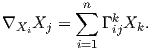
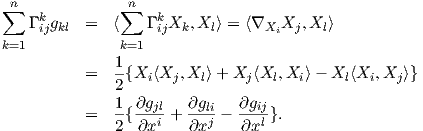
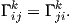
Πρόταση 5.4: ΄Εστω (U;x1,…,xn) είναι ένα τοπικό σύστημα συντεταγμένων σε μια πολλαπλότητα
Riemann και έστω Xi = 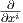 . Τότε ισχύουν τα εξής:
. Τότε ισχύουν τα εξής:
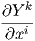 + ∑
j=1nΓ
ijkY j}X
k.
+ ∑
j=1nΓ
ijkY j}X
k.
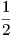 ∑
l=1ngkl{
∑
l=1ngkl{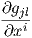 +
+ 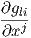 -
-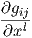 }.
}.Παραδείγματα.
1. Θεωρούμε τον ℝn εφοδιασμένον με την Ευκλείδεια μετρική gij = δij. Από την Πρόταση 5.4 (ii) προκύπτει ότι Γijk = 0, για κάθε 1 ≤ i,j,k ≤ n.
2. Μια κανονική επιφάνεια M στον ℝ3 εφοδιασμένη με την επαγόμενη Ευκλείδεια μετρική g = ⟨ , ⟩, είναι μια πολλαπλότητα Riemann διάστασης 2. Συμβολίζοντας τις συντεταγμένες της M με u,υ, τότε οι συνιστώσες της μετρικής συμβολίζονται κατά τον κλασικό τρόπο ως
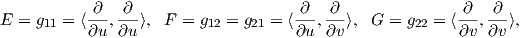
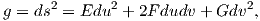
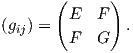
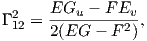
3. (Η συνοχή Levi-Civita σε μια επιφάνεια.) ΄Εστω M μια κανονική επιφάνεια στον ℝ3. Σε κάθε σημείο p ∈ M θεωρούμε την κάθετη ευθεία εp στην M που διέρχεται από το σημείο p. Η ευθεία αυτή είναι κάθετη στον εφαπτόμενο χώρο TpM, συνεπώς ως προς το κανονική Ευκλείδεια μετρική ⟨ , ⟩ ορίζεται η ορθογώνια διάσπαση
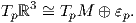
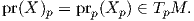
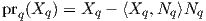
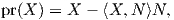
΄Εστω τώρα X,Y δύο λεία διανυσματικά πεδία στην επιφάνεια M και p ∈ M. Τότε η παράγωγος κατά κατεύθυνση DXpY δεν ανήκει απαραίτητα στον εφαπτόμενο χώρο TpM, οπότε ορίζουμε
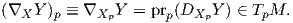
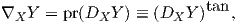
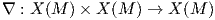
Η κεντρική μας επιδίωξη στη συνέχεια, είναι να ορίσουμε σε μια πολλαπλότητα Riemann το ανάλογο της ευθείας σε έναν Ευκλείδειο χωρο. ϒπάρχουν δύο συνηθισμένοι τρόποι χαρακτηρισμού μιας ευθείας σε έναν Ευκλείδειο χώρο:
(1) Μια ευθεία είναι η πιο ‘ίσια’ γραμμή, υπό την έννοια ότι επιδέχεται μια παραμέτρηση ώστε το πεδίο
ταχύτητας της καμπύλης να είναι σταθερό, ή διαφορετικά να είναι παράλληλο. Πράγματι, αν γ(t) = p + tυ,
(p,υ ∈ ℝn) είναι μια παραμέτρηση μιας ευθείας στον ℝn, τότε αυτή χαρακτηρίζεται από το ότι η
επιτάχυνσή της γ′′ είναι ταυτοτικά μηδέν. Ισοδύναμα, αν T(t) = γ′(t) είναι το εφαπτόμενο διάνυσμα κατά
μήκος της γ, τότε η γ′′(t) ισούται με την συναλλοίωτη παράγωγο 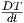 ως προς την Ευκλείδεια συνοχή
D.
ως προς την Ευκλείδεια συνοχή
D.
(2) Μια ευθεία η οποία διέρχεται από δύο σημεία αποτελεί την ελάχιστη απόσταση μεταξύ των σημείων αυτών.
Οι παραπάνω ιδιότητες δεν είναι απαραίτητα ισοδύναμες σε μια πολλαπλότητα Riemann. Θα ακολουθήσουμε την γενίκευση του χαρακτηρισμού (1) και θα ορίσουμε μια γεωδαισιακή καμπύλη γενικεύοντας την έννοια της πιο ίσιας γραμμής, οπότε χρειαζόμαστε να μελετήσουμε την έννοια της παραλληλίας, μια από τις πιο λεπτές έννοιες της γεωμετρίας Riemann. Για τον σκοπό αυτό, δεν χρειάζεται να έχουμε διαθέσιμη μια μετρική, αλλά απλώς μια πολλαπλότητα εφοδιασμένη με μια ομοπαραλληλική συνοχή. Επειδή όμως σε μια πολλαπλότητα Riemann υπάρχει μοναδική συνοχή συμβατή με την μετρική, η συνοχή Levi-Civita, θα χρησιμοποιήσουμε αυτή ακριβώς την συνοχή για να ορίσουμε την γεωδαισιακή.
΄Οσον αφορά την γενίκευση του χαρακτηρισμού (2) δεν θα ασχοληθούμε εδώ. Αναφέρουμε μόνο ότι οι γεωδαισιακές καμπύλες σε μια πολλαπλότητα Riemann προκύπτουν ως κρίσιμα σημεία του συναρτησοειδούς ενέργειας (energy functional) (υπάρχει φυσική ερμηνεία για την ορολογία αυτή). Μέσω της προσέγγισης αυτής, προκύπτει ότι τοπικά οι γεωδαισιακές καμπύλες ελάχιστοποιούν το μήκος μεταξύ των άκρων τους.
Ορισμός 5.10: ΄Εστω M μια πολλαπλότητα και γ : I → M μια καμπύλη. ΄Ενα διανυσματικό πεδίο X κατά μήκος της καμπύλης γ είναι μια απεικόνιση
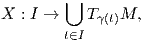
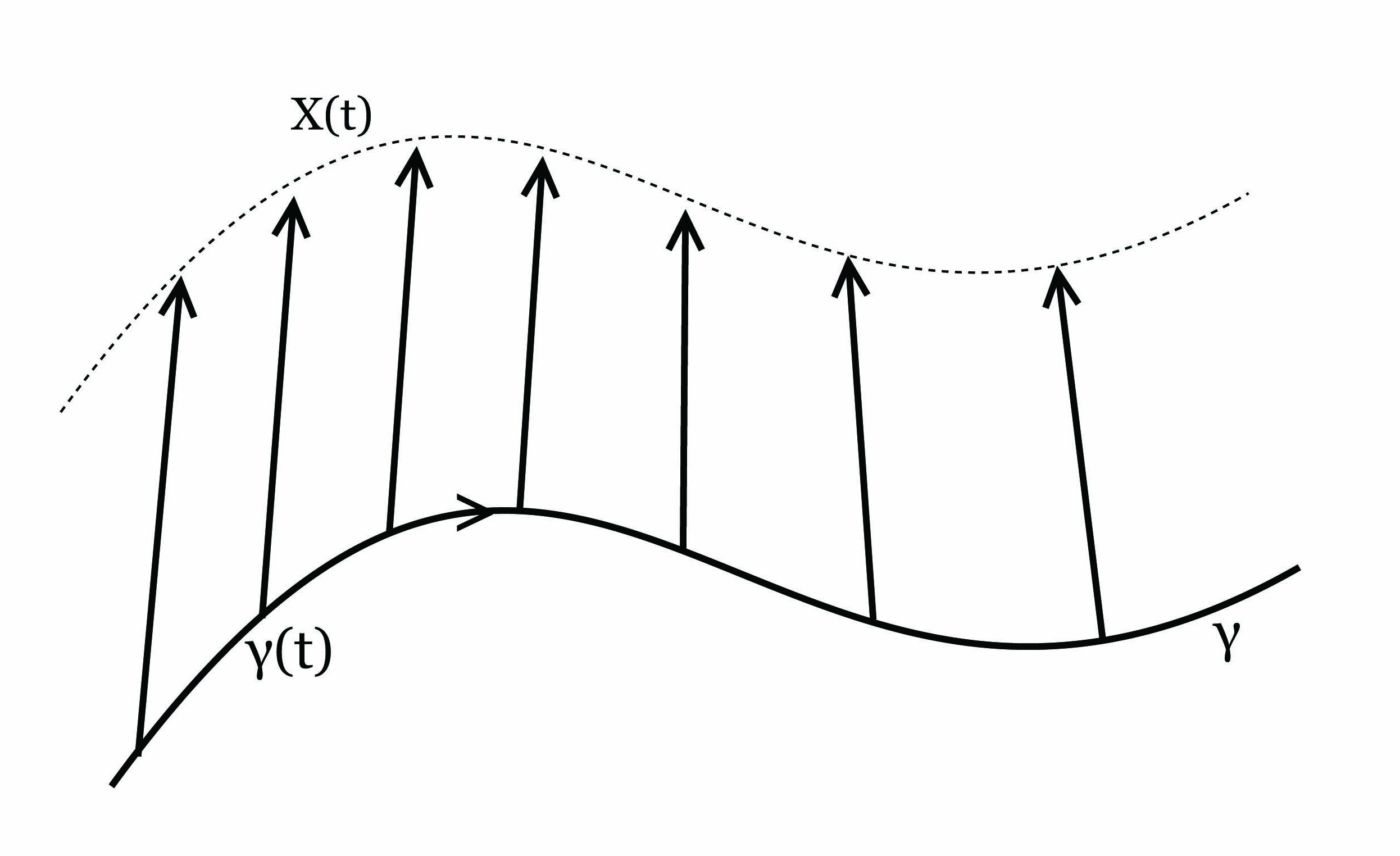
Συμβολίζουμε με X(γ) το σύνολο όλων των λείων διανυσματικών πεδίων κατά μήκος της καμπυλης γ. Για κάθε X,Y ∈ X(γ),f ∈ F(I) οι πράξεις
εφοδιάζουν το σύνολο X(γ) με δομή ενός προτύπου επί του δακτυλίου F(I).
Παράδειγμα. Αν γ : I → M είναι μια καμπύλη σε μια πολλαπλότητα, τότε το πεδίο ταχυτήτων X(t) = γ′(t) είναι ένα διανυσματικό πεδίο κατά μήκος της γ.
Θέλουμε τώρα να ορίσουμε μια έννοια παραγώγισης ενός διανυσματικού πεδίου κατά μήκος μιας καμπύλης σε μια πολλαπλότητα. Ο λόγος είναι ότι έτσι θα ορίσουμε ένα διανυσματικό πεδίο ως παράλληλο, εάν η παράγωγος αυτή είναι μηδέν. Ως συνήθως το γνωστικό κίνητρο προέρχεται από το σχετικό φαινόμενο στον ℝn.
΄Εστω X(t) = ∑
iXi(t)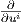 ένα λείο διανυσματικό πεδίο κατά μήκος μιας λείας καμπύλης γ(t) στον ℝn. Τότε
ορίζεται η παράγωγος
ένα λείο διανυσματικό πεδίο κατά μήκος μιας λείας καμπύλης γ(t) στον ℝn. Τότε
ορίζεται η παράγωγος 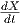 του X ως το πεδίο
του X ως το πεδίο
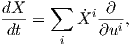
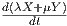 = λ
= λ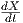 + μ
+ μ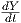 , λ,μ ∈ ℝ,
, λ,μ ∈ ℝ,
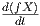 =
= 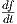 X + f
X + f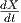 , f ∈ X(I).
, f ∈ X(I).
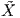 ∈ X(ℝn), υπό την έννοια ότι
X(t) =
∈ X(ℝn), υπό την έννοια ότι
X(t) = 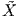 γ(t) και εάν D είναι η παράγωγος κατά κατεύθυνση στον ℝn, τότε
γ(t) και εάν D είναι η παράγωγος κατά κατεύθυνση στον ℝn, τότε
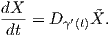
Το επόμενο αποτέλεσμα εξασφαλίζει την ύπαρξη ενός ανάλογου τελεστή παραγώγισης σε μια πολλαπλότητα εφοδιασμένη με μια ομοπαραλληλική συνοχή (άρα και σε μια πολλαπλότητα Riemann). Παραλείπουμε την απόδειξη.
Θεώρημα 5.4: ΄Εστω M μια λεία πολλαπλότητα εφοδιασμένη με μια ομοπαραλληλική συνοχή ∇ και έστω γ : I → M μια λεία καμπύλη στην M. Τότε υπάρχει μοναδική απεικόνιση (τελεστής)
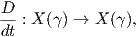
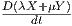 = λ
= λ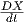 + μ
+ μ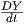 , λ,μ ∈ ℝ, X,Y ∈ X(γ), (ℝ-γραμμικότητα).
, λ,μ ∈ ℝ, X,Y ∈ X(γ), (ℝ-γραμμικότητα).
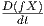 =
= 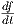 X + f
X + f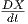 , f ∈ X(I), (Κανόνας Leibnitz).
, f ∈ X(I), (Κανόνας Leibnitz).
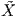 ∈ X(M), υπό την έννοια ότι
X(t) =
∈ X(M), υπό την έννοια ότι
X(t) = 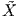 γ(t), τότε
γ(t), τότε
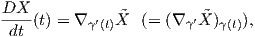
Το διανυσματικό πεδίο 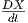 ονομάζεται συναλλοίωτη παράγωγος (ως προς τη συνοχή ∇) του διανυσματικού
πεδίου X κατά μήκος της καμπύλης γ(t) στην M ή πιο σύντομα επαγόμενη συναλλοίωτη παράγωγος. Πολλές
φορές, αυτό συμβολίζεται και με X′.
ονομάζεται συναλλοίωτη παράγωγος (ως προς τη συνοχή ∇) του διανυσματικού
πεδίου X κατά μήκος της καμπύλης γ(t) στην M ή πιο σύντομα επαγόμενη συναλλοίωτη παράγωγος. Πολλές
φορές, αυτό συμβολίζεται και με X′.
Ορισμός 5.11: ΄Εστω (M,g) μια λεία πολλαπλότητα Riemann και γ : I → M μια λεία καμπύλη. ΄Ενα διανυσματικό πεδίο X κατά μήκος της γ ονομάζεται παράλληλο εάν ισχύει
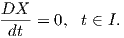
Παράδειγμα. (Συναλλοίωτη παράγωγος σε μια επιφάνεια.) ΄Εστω M μια κανονική επιφάνεια στον ℝ3 εφοδιασμένη με την συνοχή Levi-Civita
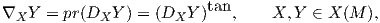
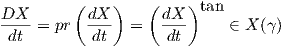
Παρατήρηση. Λόγω της ιδιότητας ∇fZX = f∇ZX της συνοχής, καθώς και της ιδιότητας (iii) του Θεωρήματος
5.4, η τιμή (∇ZX)p του πεδίου ∇ZX στο σημείο p εξαρτάται μόνο από τις τιμές Zp του πεδίου Z στο σημείο p και
του πεδίου X κατά μήκος κάποιας καμπύλης γ, τέτοια ώστε γ(0) = p και γ′(0) = Zp. Συνεπώς, μπορούμε να
χρησιμοποιούμε τον συμβολισμό ∇γ′X για το 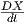 .
.
Θα αποδείξουμε τώρα το παρακάτω ιδιαίτερα χρήσιμο θεώρημα.
Θεώρημα 5.5: ΄Εστω (M,g) μια πολλαπλότητα Riemann και ∇ μια ομοπαραλληλική συνοχή στην M συμβατή με την μετρική (όχι απαραίτητα μηδενικής στρέψης). Αν γ : I → M είναι μια λεία καμπύλη στην M, τότε για οποιαδήποτε διανυσματικά πεδία V,W κατά μήκος της γ ισχύει ότι
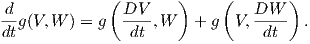
Απόδειξη. Αρκεί να αποδείξουμε την ισότητα τοπικά. ΄Εστω (U;x1,…,xn) ένας τοπικός χάρτης ο οποίος
περιέχει την καμπύλη γ και έστω {X1,…,Xn}, (Xi = 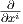 ) ένα τοπικό πλαίσιο κατά μήκος της γ. Τότε στο
γ(t) (δηλαδή κατά μήκος της γ) έχουμε ότι
) ένα τοπικό πλαίσιο κατά μήκος της γ. Τότε στο
γ(t) (δηλαδή κατά μήκος της γ) έχουμε ότι

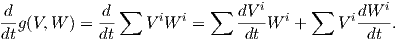
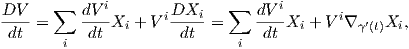
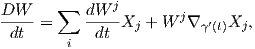
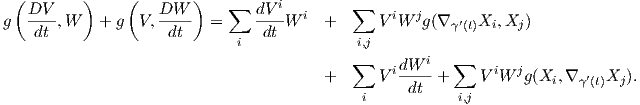
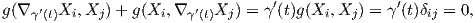
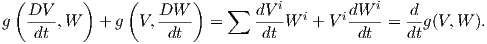
Παράδειγμα. ΄Εστω ∇ η παράγωγος κατά κατεύθυνση στον ℝn και V (t) = ∑
V i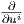 ένα διανυσματικό πεδίο κατά
μήκος μιας λείας καμπύλης γ(t) στον ℝn. Τότε η συναλλοίωτη παράγωγος είναι
ένα διανυσματικό πεδίο κατά
μήκος μιας λείας καμπύλης γ(t) στον ℝn. Τότε η συναλλοίωτη παράγωγος είναι
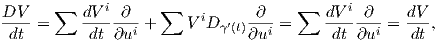
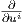 = 0 (γιατί;).
= 0 (γιατί;).
Είμαστε τώρα σε θέση να δώσουμε τον ορισμό της γεωδαισιακής καμπύλης.
Ορισμός 5.12: ΄Εστω (M,g) μια πολλαπλότητα Riemann. Μια λεία καμπύλη γ : I → M ονομάζεται γεωδαισιακή, εάν ισχύει
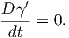
Παρατηρήσεις.
1. Γενικά για να οριστούν οι έννοιες της παραλληλίας και της γεωδαισιακής αρκεί η ύπαρξη μιας ομοπαραλληλικής συνοχής (όχι απαραίτητα η συνοχή Levi-Civita). Τότε οι ορισμοί παραλληλίας και γεωδαισιακής γράφονται ως ∇γ′X = 0 και ∇γ′γ′ = 0 αντίστοιχα. ΄Οπως και να έχει, όταν δουλεύουμε με μια πολλαπλότητα Riemann τότε χρησιμοποιούμε κατά κανόνα την συνοχή Levi-Civita.
2. ΄Ενα παράλληλο διανυσματικό πεδίο κατά μήκος μιας καμπύλης είναι το ανάλογο ενός σταθερού διανυσματικού πεδίου στον ℝn. Συνεπώς, μια γεωδαισιακή καμπύλη γ είναι μια καμπύλη, της οποίας το εφαπτόμενο διανυσματικό πεδίο γ′(t) είναι παράλληλο κατά μήκος της γ.
Το παρακάτω αποτέλεσμα είναι ανάλογο γνωστού αποτελέσματος της θεωρίας επιφανειών ([14]).
Πρόταση 5.5: ΄Εστω (M,g) μια πολλαπλότητα Riemann, γ : I → M μια λεία καμπύλη και X,Y παράλληλα
διανυσματικά πεδία κατά μήκος της γ. Τότε η συνάρτηση g(X,Y ) : I → ℝ με t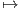 gγ(t)(Xγ(t),Y γ(t)) είναι
σταθερή και ισοδύναμα το μήκος ||X(t)|| =
gγ(t)(Xγ(t),Y γ(t)) είναι
σταθερή και ισοδύναμα το μήκος ||X(t)|| = 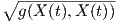 είναι σταθερό. Ιδικότερα, εάν η καμπύλη γ
είναι μια γεωδαισιακή, τότε η συνάρτηση g(γ′,γ′) είναι σταθερή κατά μήκος της γ.
είναι σταθερό. Ιδικότερα, εάν η καμπύλη γ
είναι μια γεωδαισιακή, τότε η συνάρτηση g(γ′,γ′) είναι σταθερή κατά μήκος της γ.
Απόδειξη. Χρησιμοποιούμε το γεγονός ότι η συνοχή Levi-Civita είναι συμβατή με την μετρική και το Θεώρημα 5.4 και παίρνουμε την ισότητα
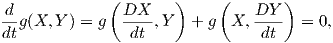
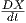 = 0 και
= 0 και 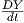 = 0. Συνεπώς, η συνάρτηση g(X,Y ) είναι σταθερή κατά μήκος της γ. ▄
= 0. Συνεπώς, η συνάρτηση g(X,Y ) είναι σταθερή κατά μήκος της γ. ▄
Η ύπαρξη μιας παράλληλης μεταφοράς, καθώς και μιας γεωδαισιακής καμπύλης, εξασφαλίζονται από τα παρακάτω θεωρήματα, για τις αποδείξεις των οποίων παραπέμπουμε στα βιβλία [3], [5], [10], [12]. Εδώ θα κάνουμε διάφορους σχολιασμούς.
Θεώρημα 5.6: ΄Εστω (M,g) μια πολλαπλότητα Riemann και έστω γ : I → M μια λεία καμπύλη στην M. Τότε για κάθε t0 ∈ I και X0 ∈ Tγ(t0)M υπάρχει μοναδικό παράλληλο διανυσματικό πεδίο Y κατά μήκος της γ τέτοιο ώστε X0 = Y (t0).
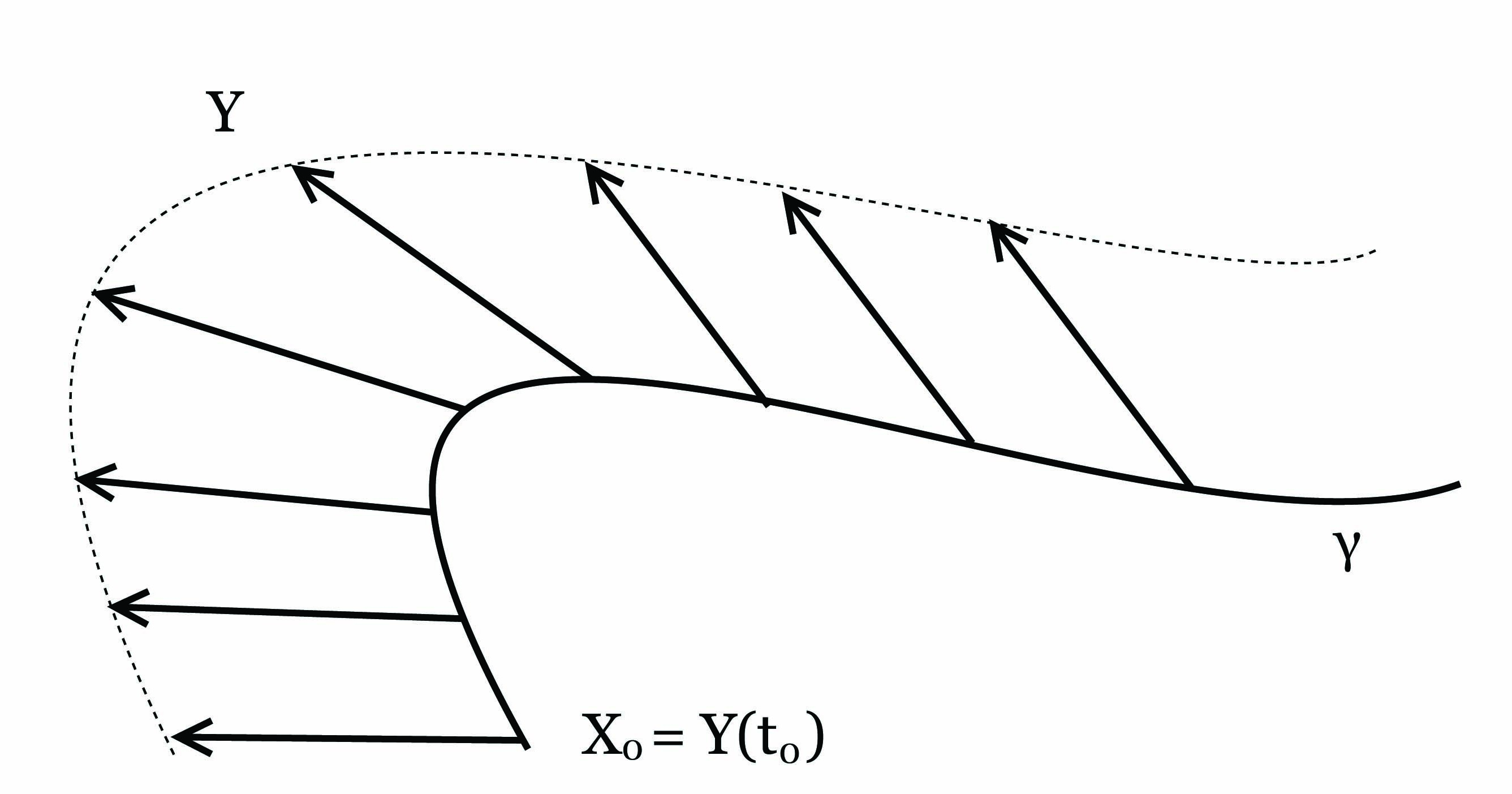
Θεώρημα 5.7: ΄Εστω (M,g) μια πολλαπλότητα Riemann. Τότε για κάθε p ∈ M και για κάθε εφαπτόμενο διάνυσμα υ ∈ TpM, υπάρχει γεωδαισιακή καμπύλη γ : (-ϵ,ϵ) → M, τέτοια ώστε γ(0) = p και γ′(0) = υ. Το διάστημα (-ϵ,ϵ) μπορεί να γίνει το μέγιστο δυνατό (μεγιστική γεωδαισιακή - maximal geodesic). Επιπλέον, η γεωδαισιακή αυτή είναι μοναδική, υπό την έννοια ότι κάθε άλλη γεωδαισιακή που ικανοποιεί τις ίδιες αρχικές συνθήκες, θα ταυτίζεται με την γ(t) στην τομή των πεδίων ορισμού τους.
Μια πολλαπλότητα Riemann (M,g) ονομάζεται πλήρης, εάν κάθε γεωδαισιακή καμπύλη έχει πεδίο ορισμού το ℝ.
Από τις διατυπώσεις των θεωρημάτων ενδεχομένως να διαφαίνεται ότι πρόκειται περί θεωρημάτων που σχετίζονται με ύπαρξη και μοναδικότητα λύσης μιας διαφορικής εξίσωσης με αρχική συνθήκη ([4]). Πράγματι, πρόκειται περί συστημάτων διαφορικών εξισώσεων, όπου στην περίπτωση των γεωδαισικών ένα τέτοιο σύστημα εκφράζεται ως εξής:
΄Εστω (U;φ = (x1,…,xn)) ένας τοπικός χάρτης της πολλαπλότητας (M,g) και θεωρούμε ως προς τον χάρτη αυτό τα σύμβολα Christoffel Γijk. ΄Εστω γ : I → M μια λεία καμπύλη. Τότε στον χάρτη U η καμπύλη γ έχει την παρακάτω τοπική αναπαράσταση
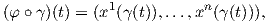
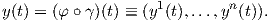
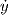 i =
i = 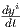 και
και 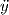 i =
i = 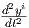 . Τότε η καμπύλη γ(t) είναι μια γεωδαισιακή εάν και μόνο εάν ισχύει το
παρακάτω σύστημα n το πλήθος διαφορικών εξισώσεων:
. Τότε η καμπύλη γ(t) είναι μια γεωδαισιακή εάν και μόνο εάν ισχύει το
παρακάτω σύστημα n το πλήθος διαφορικών εξισώσεων:
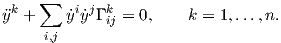 | (5.8) |
Ανάλογο σύστημα διαφορικών εξισώσεων προκύπτει για ένα παράλληλο διανυσματικό πεδίο X(t) = ∑
iXi(t)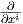 κατά μήκος μιας καμπύλης γ, όπως φαίνεται παρακάτω:
κατά μήκος μιας καμπύλης γ, όπως φαίνεται παρακάτω:
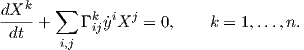 | (5.9) |
Η παράλληλη μεταφορά μας επιτρέπει να σχετίσουμε εφαπτόμενους χώρους σε δύο σημεία μιας πολλαπλότητας Riemann M, τα οποία βρίσκονται σε μια λεία καμπύλη στην M. Πράγματι, έστω γ : [a,b] → M μια λεία καμπύλη, έστω p = γ(a),q = γ(b) και x ∈ TpM. ΄Εστω X(t) το μοναδικό παράλληλο διανυσματικό πεδίο κατά μήκος της γ(t) τέτοιο ώστε X(a) = x. Τότε η συνάρτηση
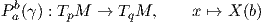
Παραδείγματα.
1. ΄Εστω En = (ℝn,⟨ , ⟩ℝn) ο Ευκλείδειος χώρος. Ως προς τον μοναδικό χάρτη (ℝn,Idℝn) η μετρική έχει τοπική αναπαράσταση gij = δij, συνεπώς
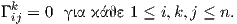
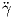 (t) = 0. Για p ∈ ℝn και υ ∈ Tpℝn
(t) = 0. Για p ∈ ℝn και υ ∈ Tpℝn ℝn
ορίζουμε
ℝn
ορίζουμε
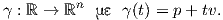
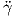 (t) = 0. Συνεπώς, σύμφωνα με το Θεώρημα 5.7 οι γεωδαισιακές καμπύλες στον ℝn
είναι οι ευθείες και μόνο αυτές.
(t) = 0. Συνεπώς, σύμφωνα με το Θεώρημα 5.7 οι γεωδαισιακές καμπύλες στον ℝn
είναι οι ευθείες και μόνο αυτές.
2. ΄Εστω S2 η μοναδιαία σφαίρα στον ℝ3 και έστω γ(t) ένας μέγιστος κύκλος με παραμέτρηση ως προς το μήκος τόξου (δηλαδή ||γ′(t)|| = 1). Επειδή γ(t) ∈ S2, ισχύει ⟨γ(t),γ(t)⟩ = 1 και με παραγώγιση της ισότητας αυτής προκύπτει ότι
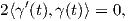
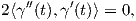
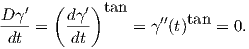
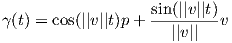
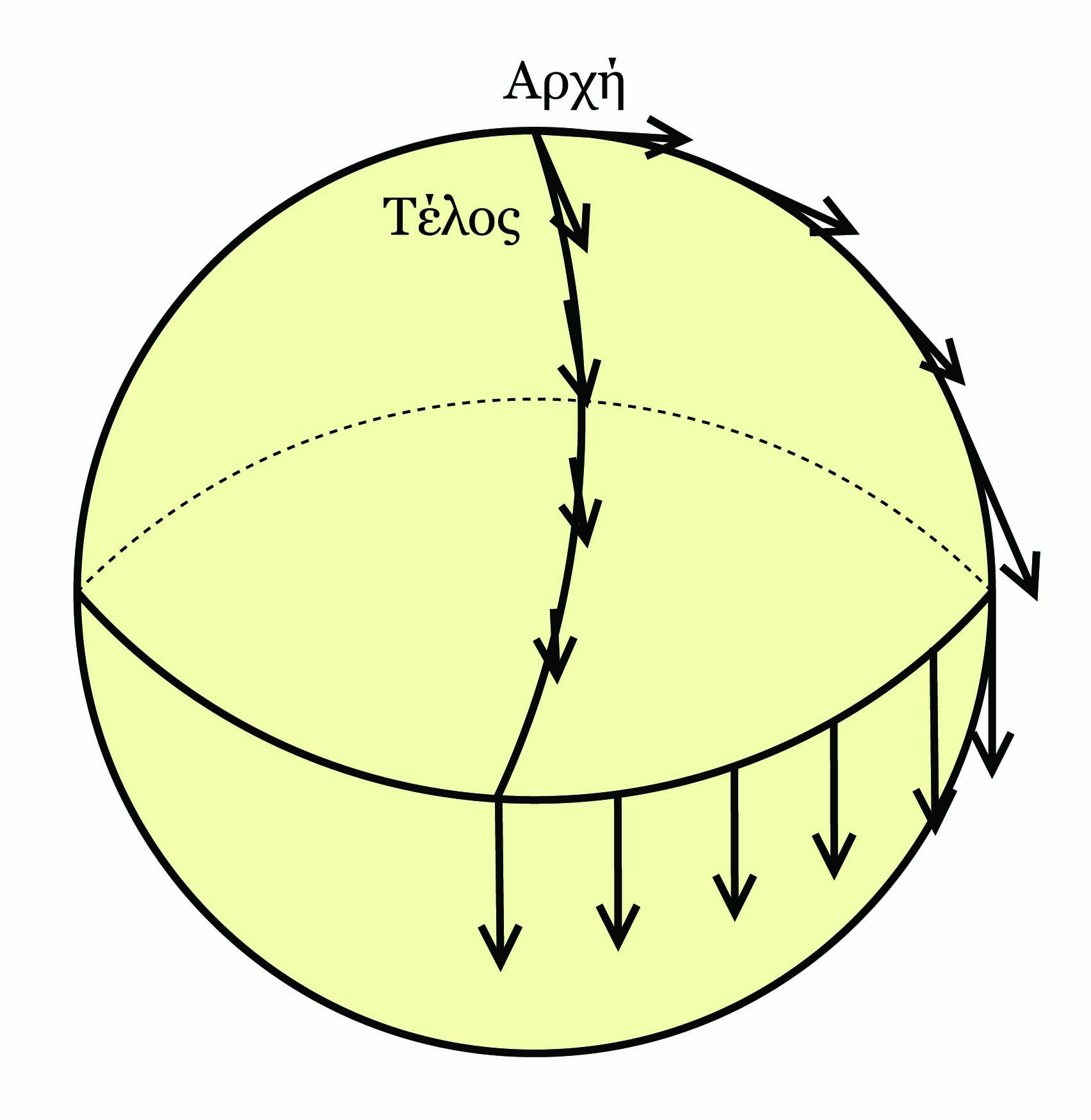
3. Η παράλληλη μεταφορά σε έναν Ευκλείδειο χώρο είναι ανεξάρτητη του δρόμου. Αυτό σημαίνει ότι η διεύθυνση ενός διανύσματος που μετακινείται παράλληλα με τον εαυτό του κατά μήκος μιας καμπύλης διατηρείται σταθερή. Αυτό όμως δεν συμβαίνει γενικά σε μια επιφάνεια. ΄Ετσι για παράδειγμα στην σφαίρα, η παράλληλη μεταφορά ενός εφαπτόμενου διανύσματος από τον βόρειο πόλο κατά μήκος μιας κλειστής καμπύλης που αποτελείται από τόξα μέγιστων κύκλων και η επιστροφή σε αυτόν, θα έχει ως αποτέλεσμα την αλλαγή της διεύθυνσης του διανύσματος. Το φαινόμενο αυτό σχετίζεται με την έννοια της μονοδρομίας σε μια πολλαπλότητα Riemann.
4. Θεωρούμε τον ℝ3 εφοδιασμένον με την μετρική
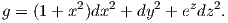
Λύση:
(i) Ο πίνακας της μετρικής, καθώς και ο αντίστροφος αυτού είναι:
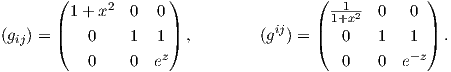 |
Θέτοντας y1 = x,y2 = y,y3 = z προκύπτει ότι τα μόνα μη μηδενικά σύμβολα Christoffel είναι οι συναρτήσεις

(ii) Χρησιμοποιώντας τα παραπάνω σύμβολα Christoffel προκύπτει ότι οι διαφορικές εξισώσεις των γεωδαισιακών (5.8) παίρνουν την εξής μορφή:
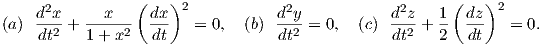 |
Οι λύσεις των παραπάνω εξισώσεων είναι οι εξής:
(a) Φέρνουμε την εξίσωση στη μορφή
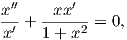
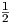 ln(1 + x2) = lnA ή ισοδύναμα x′ =
ln(1 + x2) = lnA ή ισοδύναμα x′ = 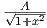 και τελικά
και τελικά
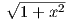 dx = At. Ολοκληρώνοντας και τα δύο μέλη παίρνουμε τη λύση σε πεπλεγμένη μορφή:
dx = At. Ολοκληρώνοντας και τα δύο μέλη παίρνουμε τη λύση σε πεπλεγμένη μορφή:
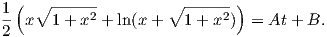
(b) Η λύση είναι y = Ct + D.
(c) Θέτουμε w = 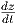 . Τότε η διαφορική εξίσωση παίρνει τη μορφή
. Τότε η διαφορική εξίσωση παίρνει τη μορφή 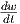 +
+ 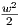 = 0, από την οποία παίρνουμε ότι
= 0, από την οποία παίρνουμε ότι
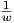 =
= 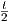 +
+ 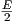 . Συνεπώς, προκύπτει ότι
. Συνεπώς, προκύπτει ότι
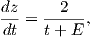
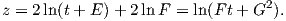
(iii) Οι διαφορικές εξισώσεις (5.9) της παράλληλης μεταφοράς ενός διανύσματος X = (X1,X2,X3) κατά μήκος της καμπύλης γ παίρνουν τη μορφή
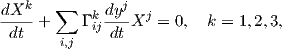
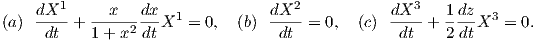 |
Κατά μήκος της καμπύλης γ(t) = (x(t),y(t),z(t)) = (t,t,t) οι παραπάνω διαφορικές εξισώσεις ανάγονται στις εξής:
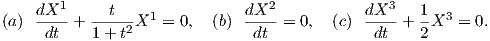 |
Ολοκληρώνοντας και λαμβάνοντας υπόψη την αρχική συνθήκη (X1(0),X2(0),X3(0)) = (a,b,c) παίρνουμε τις παρακάτω λύσεις:
(a) lnX1 = -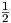 ln(1 + t2) + lnA, άρα X1 =
ln(1 + t2) + lnA, άρα X1 = 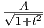 . Λόγω της συνθήκης X1(0) = a παίρνουμε ότι
X1 =
. Λόγω της συνθήκης X1(0) = a παίρνουμε ότι
X1 = 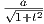 .
.
(b) X2 = A, και λόγω της X2(0) = b παίρνουμε ότι X2 = b.
(c) X3 = Ae-t∕2, απ΄ όπου παρόμοια παίρνουμε ότι X3 = ce-t∕2.
Συμπερασματικά, η παράλληλη μεταφορά του διανύσματος (a,b,c) κατά μήκος της καμπύλης γ από το σημείο
(0,0,0) καταλήγει στο διάνυσμα (X1,X2,X3) = (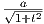 ,b,ce-t∕2).
,b,ce-t∕2).
(iv) Για να είναι η καμπύλη γ γεωδαισιακή θα πρέπει οι συντεταγμένες της να ικανοποιούν το σύστημα διαφορικών εξισώσεων που προέκυψε στο ερώτημα (ii). Θέτοντας x(t) = t,y(t) = t,z(t) = t βλέπουμε εύκολα ότι η πρώτη από τις τρεις διαφορικές εξισώσεις δεν ικανοποιείται (παρά μόνο όταν t = 0), συνεπώς η γ δεν είναι γεωδαισιακή.
(v) Από το ερώτημα (iii) έχει προκύψει το παράλληλο διανυσματικό πεδίο
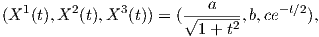
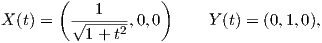
(vi) Θεωρούμε τα διανύσματα X(0) = (a,b,c) και Y (0) = (a′,b′,c′). Τότε τα διανυσματικά πεδία X(t),Y (t) που προκύπτουν με παράλληλη μεταφορά των διανυσμάτων αυτών κατά μήκος της γ, ικανοποιούν τη σχέση
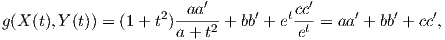
Η παρακάτω πρόταση απαντά στο ερώτημα κατά πόσον μια αναπαραμέτρηση μιας γεωδαισιακής είναι γεωδαισική
Πρόταση 5.6: ΄Εστω γ : I → M μια μη σταθερή γεωδαισιακή. Μια αναπαραμέτρηση 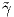 = γ ∘ u : J → M
είναι γεωδαισιακή εάν και μόνο εάν u(t) = at + b, για κάποιες πραγματικές σταθερές a,b.
= γ ∘ u : J → M
είναι γεωδαισιακή εάν και μόνο εάν u(t) = at + b, για κάποιες πραγματικές σταθερές a,b.
Ως αποτέλεσμα, είναι δυνατόν να μεταβάλουμε το μήκος του διαστήματος ορισμού μιας γεωδαισιακής, αλλάζοντας την ταχύτητα που την διατρέχουμε.
Πρόταση 5.7: ΄Εστω ότι το διάστημα (a,b) περιέχει το 0. Τότε για κάθε θετική σταθερά k ∈ ℝ+, η
καμπύλη γ(u) είναι μια γεωδαισιακή στο (a,b), τέτοια ώστε γ(0) = q και γ′(0) = υ, εάν και μόνο εάν η
καμπύλη 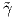 (t) = γ(kt) είναι μια γεωδαισιακή στο (a∕k,b∕k) με
(t) = γ(kt) είναι μια γεωδαισιακή στο (a∕k,b∕k) με 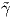 ′(0) = q και
′(0) = q και 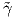 ′(0) = kυ.
′(0) = kυ.
΄Εστω γυ(t) η μοναδική μεγιστική γεωδαισιακή που διέρχεται από το σημείο q και με αρχική ταχύτητα υ ∈ TpM. Τότε από την προηγούμενη πρόταση προκύπτει ότι
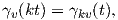
ϒπάρχουν δύο εκθετικές επεικονίσεις στη γεωμετρία: η εκθετική απεικόνιση μιας συνοχής και η εκθετική απεικόνιση μιας ομάδας Lie. Αν και οι έννοιες αυτές είναι ανεξάρτητες, εν τούτοις όταν μια ομάδα Lie επιδέχεται μια αμφιαναλλοίωτη μετρική Riemann τότε η εκθετική απεικόνιση μιας ομάδας Lie ταυτίζεται με την εκθετική απεικόνιση της συνοχής Levi-Civita (βλ. Κεφάλαιο 9).
Σύμφωνα με το Θεώρημα 5.7, σε μια πολλαπλότητα Riemann υπάρχει μοναδική γεωδαισιακή καμπύλη η οποία διέρχεται από ένα σημείο και έχει δοσμένη διεύθυνση (αρχική ταχύτητα). Η γεωδαισιακή αυτή όμως ενδέχεται να είναι πολύ μικρού μήκους, δηλαδή να ορίζεται σε ένα πολύ μικρό διάστημα (-ϵ,ϵ) το οποίο περιέχει το 0. Με κατάλληλη αναπαραμέτρηση της γεωδαισιακής (Πρόταση 5.7) το διάστημα αυτό είναι δυνατόν να μεγαλώσει, με ταυτόχρονη μείωση του μέτρου της αρχικής ταχύτητας.
Προκειμένου να ορίσουμε την εκθετική απεικόνιση σε ένα σημείο p μιας πολλαπλότητα Riemann, θα εργαστούμε ως εξής: Θα βρούμε μια περιοχή του p για την οποία υπάρχει ένα ομοιόμορφο φράγμα (αριθμός), έτσι ώστε όλες οι γεωδαισιακές με αρχή οποιοδήποτε σημείο στην περιοχή αυτή και αρχική ταχύτητα μήκους μικρότερου από το φράγμα αυτό, να έχουν ένα κοινό διάστημα ορισμού.
΄Εστω (M,g) μια πολλαπλότητα Riemann διάστασης n και p ∈ M. ΄Εστω
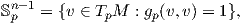
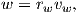
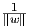 w. Για κάθε υ ∈ Spn-1 έστω γυ : (-αυ,βυ) → M η μεγιστική γεωδαισιακή
καμπύλη τέτοια ώστε αυ,βυ ∈ ℝ+ ∪{∞}, γυ(0) = p και
w. Για κάθε υ ∈ Spn-1 έστω γυ : (-αυ,βυ) → M η μεγιστική γεωδαισιακή
καμπύλη τέτοια ώστε αυ,βυ ∈ ℝ+ ∪{∞}, γυ(0) = p και 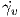 (0) = υ. Αποδεικνύεται ότι ο πραγματικός
αριθμός
(0) = υ. Αποδεικνύεται ότι ο πραγματικός
αριθμός
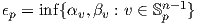
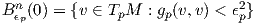
Ορισμός 5.13: Η εκθετική απεικόνιση (exponetial map) expp : Bϵpn(0) ⊂ TpM → M στο σημείο p ορίζεται ως
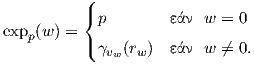
Παρατηρήσεις.
1. Ο όρος εκθετική απεικόνιση εξηγείται καλύτερα μελετώντας γεωδαισιακές καμπύλες σε ομάδες πινάκων, όπως για παράδειγμα η ορθογώνια ομάδα O(n). Τότε αποδεικνύεται ότι η αντίστοιχη εκθετική απεικόνιση στο ουδέτερο σημείο I ∈ O(n) (ταυτοτικός πίνακας) δίνεται ως η συνηθισμένη εκθετική απεικόνιση πινάκων, δηλαδή expI(A) = eA, A ∈ TIO(n).
2. Αν υ ∈ Spn-1, τότε το ευθύγραμμο τμήμα λυ : (-ϵp,ϵ) → TpM, λυ(t) = tυ απεικονίζεται μέσω της εκθετικής απεικόνισης στη γεωδαισιακή γυ, δηλαδή τοπικά ισχύει γυ = expp ∘ λυ. Συνεπώς, τοπικά η εκθετική απεικόνιση απεικονίζει ευθείες σε γεωδαισιακές.
Αποδεικνύεται ότι η απεικόνιση expp είναι διαφορίσιμη και ότι το διαφορικό d(expp)0 : TpM → TpM ισούται με την ταυτοτική απεικόνιση IdTpM στον εφαπτόμενο χώρο TpM. Συνεπώς, από το θεώρημα αντίστροφης συνάρτησης υπάρχει rp ∈ ℝ+, έτσι ώστε αν Up = Brpn(0) και V p = expp(Up), τότε η απεικόνιση expp|Up : Up → V p να είναι αμφιδιαφόριση. Η απεικόνιση αυτή παραμετρικοποιεί το ανοικτό υποσύνολο V p της πολλαπλότητας M, το οποίο ορίζει έναν χάρτη στην M, οποίος ονομάζεται κανονική περιοχή (normal neighborhood) του p ∈ M.
Παράδειγμα. ΄Εστω S2 η μοναδιαία σφαίρα του ℝ3 και p = (1,0,0) ο βόρειος πόλος. Τότε ο μοναδιαίος κύκλος στον εφαπτόμενο χώρο TpS2 δίνεται ως
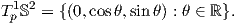
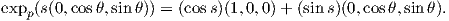
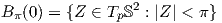
1. ΄Εστω (V,⟨ , ⟩) ένας διανυσματικός χώρος με εσωτερικό γινόμενο και έστω u,υ ∈ V . Αποδείξτε ότι
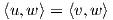
2. ΄Εστω (M,g) μια πολλαπλότητα Riemann. Αποδείξτε ότι δύο λεία διανυσματικά πεδία X,Y ∈ X(M) είναι ίσα, εάν και μόνο εάν ισχύει
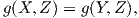
3. Αποδείξτε ότι η στερεογραφική προβολή
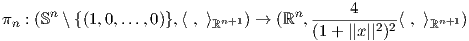
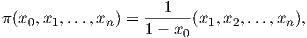
4. Θεωρούμε το άνω ημιεπίπεδο ℍ2 = {(x,y) ∈ ℝ2 : y > 0}. Σε κάθε σημείο p = (x,y) ∈ ℍ2 ορίζουμε
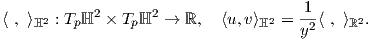
(α) Αποδείξτε ότι η απεικόνιση ⟨ , ⟩ℍ2 ορίζει μια μετρική Riemann στο ℍ2. Η πολλαπλότητα Riemann (ℍ2,⟨ , ⟩ℍ2) ονομάζεται υπερβολικός χώρος.
(β) ϒπολογίστε τα σύμβολα Christoffel της μετρικής ⟨ , ⟩ℍ2.
(γ) Αποδείξτε ότι οι κάθετες ευθείες x = c είναι γεωδαισιακές καμπύλες με πεδίο ορισμού το ℝ. Συμβουλευτείτε την βιβλιογραφία ή ένα βιβλίο θεωρίας επιφανειών (π.χ. [12]), προκειμένου να γρείτε όλες τις γεωδαισιακές του χώρου (ℍ2,⟨ , ⟩ℍ2).
5. Εφοδιάζουμε τον ανοικτό μοναδιαίο δίσκο B12(0) του μιγαδικού επιπέδου με την μετρική
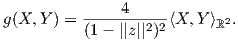
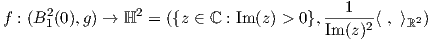
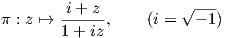
6. Συμπληρώστε την απόδειξη του Θεωρήματος 5.3. Συγκεκριμένα, αποδείξτε ότι η συνοχή ∇XY , που ορίστηκε από τον τύπο του Koszul, ικανοποιεί τις ιδιότητες μιας ομοπαραλληλικής συνοχής, καθώς και τις σχέσεις (5.1), (5.2).
7. ΄Εστω {E1,…,En} ένα πλαίσιο της πολλαπλότητας Riemann (M,g). Αποδείξτε ότι
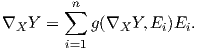
8. Θεωρούμε τον χώρο ℝ2 με την μετρική g = dx2 + dy2. Είναι η καμπύλη γ(t) = (x(t),y(t)) = (t3,t3) μια γεωδαισιακή;
9. Σε κάθε σημείο p ∈ ℝ2 θεωρούμε την φυσική ταύτιση Tpℝ2 ℝ2. Δείξτε ότι η εκθετική απεικόνιση
exp : Tpℝ2 → ℝ2 είναι η ταυτοτική απεικόνιση.
ℝ2. Δείξτε ότι η εκθετική απεικόνιση
exp : Tpℝ2 → ℝ2 είναι η ταυτοτική απεικόνιση.
[1] M. Berger, A Panoramic View of Riemannian Geometry, Springer, 2002.
[2] A. Besse, Einstein Manifolds, Springer, 2008.
[3] W. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry, 2nd ed., Academic Press, Boston, 1986.
[4] W. E. Boyce and R.C. DiPrima, Elementary Differential Equations, 10th ed., WileyPLUS, 2012.
[5] M. do Carmo, Riemannian Geometry, Birkhäuser, Boston 1992.
[6] S. Gallot, D. Hulin and J. Lafontaine, Riemannian Geometry, 3rd ed. Springer, 2004.
[7] L. Godinho and J. Natário, An Introduction to Riemannian Geometry: With Applications to Mechanics and Relativity , Springer, 2014.
[8] M. Gunther, On the perturbation problem associated to isometric embeddings of Riemannian manifolds, Ann. Global Anal. Geom. 7 (1989) 69–77.
[9] M. Gunther, Isometric embeddings of Riemannian manifolds, in: Proccedings of the International Congress of Mathematicians (Kyoto 1990), Math. Soc. Japan (1991) 1137–1143.
[10] J.M. Lee, Riemannian Manifolds: An Introduction to Curvatute, Springer, New York, 1997.
[11] J. Nash, The embedding problem for Riemannian manifolds, Ann. Math. 63 (1965) 20–63.
[12] B. O’ Neill, Semi-Riemannian Geometry with Applications to Relativity, Academic Press 1983.
[13] P. Petersen, Riemannian Geometry, Springer, New York, 1998.
[14] A.N. Pressley, Elementary Differential Geometry Geometry, 2nd ed. Springer, New York, 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.