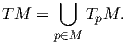
Σύνοψη
Ορίζουμε και μελετάμε λεία διανυσματικά πεδία σε μια λεία πολλαπλότητα M. Ως λεία απεικόνιση, ένα
διανυσματικό πεδίο έχει τη μορφή X : M → TM με τιμές στην εφαπτόμενη δέσμη TM, της οποίας
περιγράφουμε την τοπολογική και διαφορική δομή. Προκειμένου να χαρακτηρίσουμε τη διαφορισιμότητα
ενός διανυσματικού πεδίου, χρειαζόμαστε ένα τεχνικό εργαλείο από τη μαθηματική ανάλυση, τις
συναρτήσεις εξογκώματος. Μια τακτική χρήση των συναρτήσεων εξογκώματος στην γεωμετρία των
πολλαπλοτήτων, είναι για την επέκταση μιας λείας συνάρτησης από ένα ανοικτό υποσύνολο της M σε
ολόκληρη την πολλαπλότητα. Χρησιμοποιώντας το θεώρημα ύπαρξης και μοναδικότητας λύσης για
μια συνήθη διαφορική εξίσωση, προκύπτει ότι για κάθε διανυσματικό πεδίο σε μια πολλαπλότητα M
ορίζεται μια οικογένεια καμπυλών, οι ολοκληρωτικές καμπύλες. Τέλος, ορίζουμε μια πράξη μεταξύ δύο
διανυσματικών πεδίων, το γινόμενο Lie, μέσω του οποίου το σύνολο των λείων διανυσματικών πεδίων
σε μια πολλαπλότητα M εφοδιάζεται με τη δομή μιας άλγεβρας Lie. Η έννοια αυτή είναι ιδιαίτερα
σημαντική στην γεωμετρία και μαθηματική φυσική. Οι βασικές αναφορές είναι τα βιβλία [1], [2], [7] και
[8].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Συνήθεις Διαφορικές Εξισώσεις, Γενική Τοπολογία.
Η έννοια του λείου (διαφορίσιμου) διανυσματικού πεδίου σε μια πολλαπλότητα απαιτεί μια σχολαστικότερη προετοιμασία από αυτήν ενός διανυσματικού πεδίου σε έναν Ευκλείδειο χώρο. Θα χρειαστούμε να ορίσουμε την εφαπτόμενη δέσμη επί μιας πολλαπλότητας M και στη συνέχεια ένα εργαλείο από την ανάλυση, τις συναρτήσεις εξογκώματος. Η εφαπτόμενη δέσμη είναι μια συλλογή από εφαπτόμενους χώρους, η οποία μεταβάλλεται κατά λείο τρόπο και παραμετρικοποιείται μέσω των σημείων της M. Αποτελεί παράδειγμα μιας διανυσματικής δέσμης επί μιας πολλαπλότητας M, η οποία είναι μια συλλογή από διανυσματικούς χώρους που μεταβάλλεται κατά λείο τρόπο και παραμετρικοποιείται μέσω των σημείων της M. Οι διανυσματικές δέσμες εμφανίστηκαν λίγο μετά το 1930 και μέχρι σήμερα έχουν σημαντική θέση στην γεωμετρία και την τοπολογία.
Θα επεξεργαστούμε την εφαπτόμενη δέσμη σε τρία βήματα: ορισμός, τοπολογία και διαφορική δομή.
΄Εστω M μια λεία πολλαπλότητα. Η εφαπτόμενη δέσμη (tangent bundle) της M είναι η ένωση όλων των εφαπτόμενων χώρων της M:
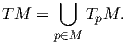
Η απεικόνιση π : TM → M με τιμή π(p,υp) = p, (υp ∈ TpM) ονομάζεται φυσική προβολή (υπό την έννοια ότι είναι ανεξάρτητη από οποιαδήποτε επιλογή, όπως άτλαντας, τοπικές συντεταγμένες, κ.λπ.).
΄Εστω (U,φ) = (U;x1,…,xn) ένας τοπικός χάρτης της M. Θεωρούμε το σύνολο
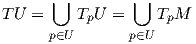
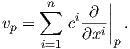
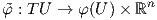
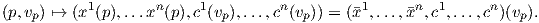
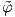 ως αντίστροφη την απεικόνιση
ως αντίστροφη την απεικόνιση
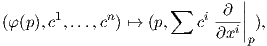
΄Ενας εναλλακτικός τρόπος γραφής της απεικόνισης 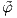 είναι
είναι 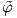 = (φ ∘ π,dφp). Πράγματι,
αν dφp : TpU → Tφ(p)ℝn
= (φ ∘ π,dφp). Πράγματι,
αν dφp : TpU → Tφ(p)ℝn ℝn είναι το διαφορικό της φ στο p, τότε λόγω της Πρότασης 3.3 είναι
dφp(υp) = ∑
ci
ℝn είναι το διαφορικό της φ στο p, τότε λόγω της Πρότασης 3.3 είναι
dφp(υp) = ∑
ci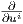 |φ(p), άρα μπορούμε να ταυτίσουμε το dφp(υp) με το διάνυσμα-στήλη (c1,…,cn) ∈ ℝn.
|φ(p), άρα μπορούμε να ταυτίσουμε το dφp(υp) με το διάνυσμα-στήλη (c1,…,cn) ∈ ℝn.
Στη συνέχεια, χρησιμοποιούμε την απεικόνιση 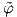 για να μεταφέρουμε την τοπολογία του φ(U) × ℝn στο
σύνολο TU ως εξής: ένα σύνολο A στο TU θα ονομάζεται ανοικτό εάν και μόνο εάν το σύνολο
για να μεταφέρουμε την τοπολογία του φ(U) × ℝn στο
σύνολο TU ως εξής: ένα σύνολο A στο TU θα ονομάζεται ανοικτό εάν και μόνο εάν το σύνολο 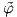 (A) είναι ανοικτό
στο φ(U) × ℝn. Το σύνολο φ(U) × ℝn έχει την κανονική τοπολογία ως ανοικτό υποσύνολο του ℝ2n. Από τον
τρόπο που ορίστηκε η τοπολογία στο TU, το σύνολο TU είναι ομοιομορφικό με το φ(U) × ℝn. Τέλος, είναι
δυνατόν να αποδειχθεί ότι με την τοπολογία αυτή, η εφαπτόμενη δέσμη TM είναι τοπολογικός χώρος Hausdorff
και έχει αριθμήσιμη βάση (βλ. για παράδειγμα [6] ή [8]).
(A) είναι ανοικτό
στο φ(U) × ℝn. Το σύνολο φ(U) × ℝn έχει την κανονική τοπολογία ως ανοικτό υποσύνολο του ℝ2n. Από τον
τρόπο που ορίστηκε η τοπολογία στο TU, το σύνολο TU είναι ομοιομορφικό με το φ(U) × ℝn. Τέλος, είναι
δυνατόν να αποδειχθεί ότι με την τοπολογία αυτή, η εφαπτόμενη δέσμη TM είναι τοπολογικός χώρος Hausdorff
και έχει αριθμήσιμη βάση (βλ. για παράδειγμα [6] ή [8]).
΄Εστω {(Uα,φα)} ένας λείος άτλαντας της πολλαπλότητας M. Θα αποδείξουμε ότι ο {(TUα,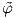 α)} είναι ένας λείος
άτλαντας της εφαπτόμενης δέσμης TM. Προφανώς ισχύει ότι TM = ⋃
αTUα, άρα αρκεί να δείξουμε τη λεία
συμβατότητα των
α)} είναι ένας λείος
άτλαντας της εφαπτόμενης δέσμης TM. Προφανώς ισχύει ότι TM = ⋃
αTUα, άρα αρκεί να δείξουμε τη λεία
συμβατότητα των 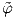 α και
α και 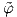 β στην τομή (TUα) ∩ (TUβ), για κάθε α,β.
β στην τομή (TUα) ∩ (TUβ), για κάθε α,β.
Θυμίζουμε ότι αν (U;x1,…,xn), (V ;y1,…,yn) είναι δύο χάρτες της M, τότε για κάθε p ∈ U ∩V υπάρχουν δύο βάσεις {∂∕∂xj|p}j=1n και {∂∕∂yi|p}i=1n του εφαπτόμενου χώρου TpM, ώστε κάθε διάνυσμα υp ∈ TpM να εκφράζεται με δύο τρόπους ως
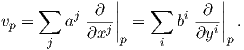 | (4.1) |
Εφαρμόζοντας και τα δύο μέλη στις συναρτήσεις yk προκύπτει ότι
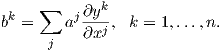 | (4.2) |
Επιστρέφουμε τώρα στον άτλαντα {(Uα,φα)} και έστω ότι φα = (x1,…,xn) και φβ = (y1,…,yn). Χρησιμοποιώντας την (4.1) βλέπουμε ότι η απεικόνιση
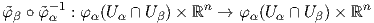
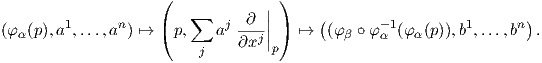
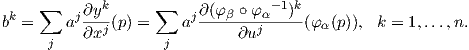
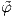 β ∘
β ∘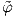 α-1 θα είναι λεία.
Καταλήξαμε λοιπόν στο ότι η εφαπτόμενη δέσμη TM είναι μια λεία πολλαπλότητα διάστασης 2n με λείο άτλαντα
τον {(TUα,
α-1 θα είναι λεία.
Καταλήξαμε λοιπόν στο ότι η εφαπτόμενη δέσμη TM είναι μια λεία πολλαπλότητα διάστασης 2n με λείο άτλαντα
τον {(TUα,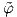 α)}.
α)}.
΄Οπως αναφέραμε νωρίτερα, η εφαπτόμενη δέσμη μιας πολλαπλότητας είναι μια ειδική περίπτωση διανυσματικής δέσμης, την οποία θα περιγράψουμε περιληπτικά.
Ορισμός 4.1: Μια λεία διανυσματική δέσμη (vector bundle) τάξης r αποτελείται από μια τριάδα (E,M,π), όπου E,M είναι λείες πολλαπλότητες και π : E → M είναι μια λεία και επί απεικόνιση, η οποία είναι τοπικά τετριμμένη. Η απεικόνιση π ονομάζεται προβολή. Οι πολλαπλότητες E και M ονομάζονται αντίστοιχα ολικός χώρος (total space) και χώρος βάσης (base space) της διανυσματικής δέσμης. Για συντομία λέμε ότι η πολλαπλότητα E είναι μια διανυσματική δέσμη επί της πολλαπλότητας M (vector bundle over M).
Για κάθε p ∈ M η αντίστροφη εικόνα π-1(p) := π-1({p}) ονομάζεται νήμα της δέσμης στο σημείο p (fiber at p). Το νήμα στο σημείο p συμβολίζεται τακτικά και με Ep.
Ο όρος ότι η διανυσματική δέσμη είναι τοπικά τετριμμένη σημαίνει το εξής:
(i) Για κάθε p ∈ M το νήμα π-1(p) είναι ένας διανυσματικός χώρος διάστασης r.
(ii) Για κάθε p ∈ M υπάρχουν ανοικτή περιοχή U του p και αμφιδιαφόριση φ : π-1(U) → U × ℝr, τέτοια ώστε για κάθε q ∈ U ο περιορισμός
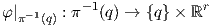
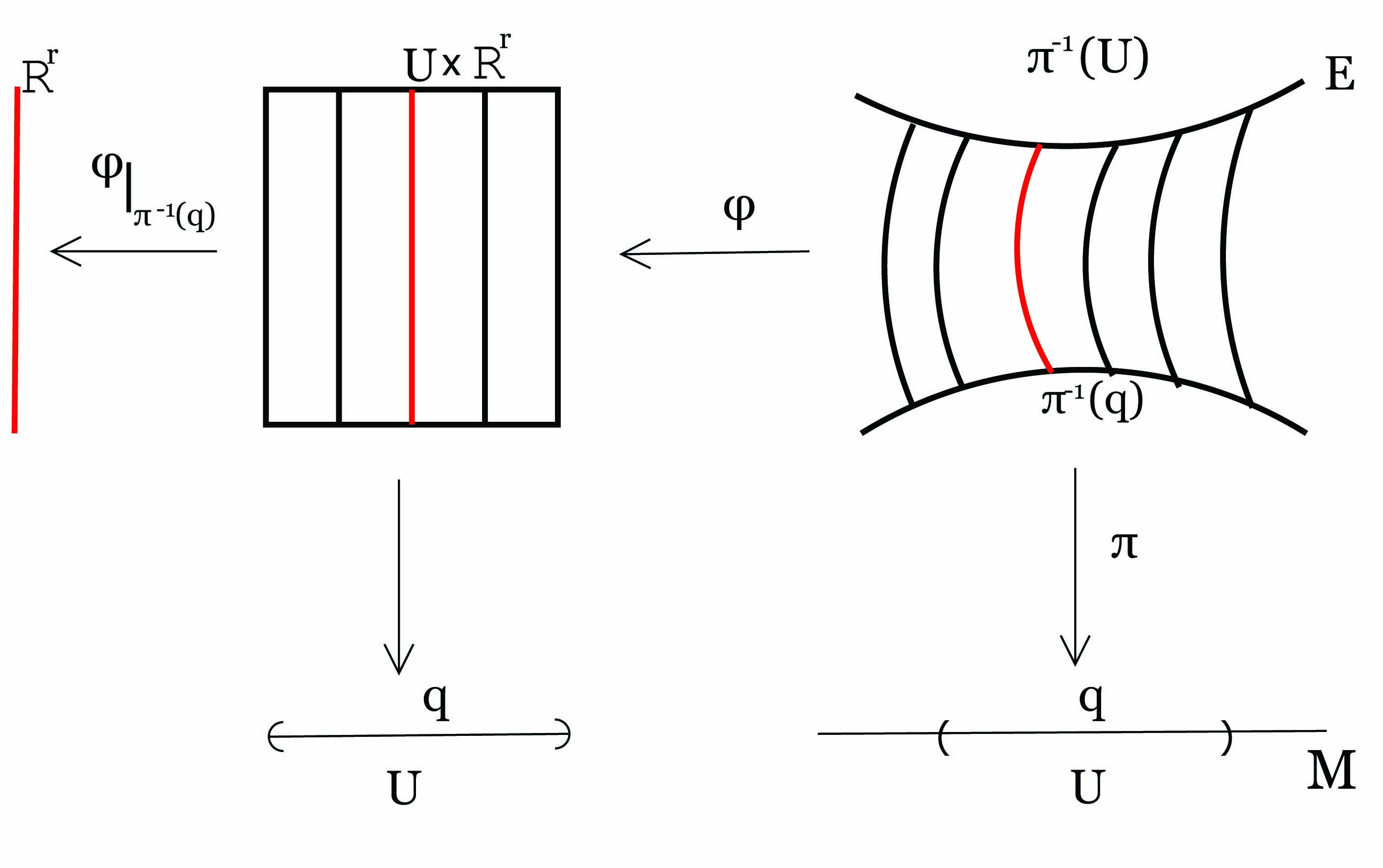
Μια τομή (section) μιας διανυσματικής δέσμης π : E → M είναι μια απεικόνιση s : M → E τέτοια ώστε π ∘ s = IdM. Μια τομή ονομάζεται λεία εάν είναι μια λεία απεικόνιση μεταξύ των πολλαπλοτήτων M και E.
Δύο εξαιρετικά χρήσιμα τεχνικά εργαλεία στην θεωρία πολλαπλοτήτων αποτελούν οι συναρτήσεις εξογκώματος (bump functions) και η διαμέριση της μονάδας. Οι συναρτήσεις εξογκώματος θα χρησιμοποιηθούν για να κατασκευαστούν λείες συναρτήσεις από μια περιοχή ενός σημείου σε ολόκληρη την πολλαπλότητα. Η διαμέριση της μονάδας χρησιμοποιείται συνήθως με δύο τρόπους: (α) για την έκφραση ενός αντικειμένου που ορίζεται σε ολόκληρη την πολλαπλότητα, σε ένα τοπικά πεπερασμένο άθροισμα από τοπικά αντικείμενα στα ανοικτά σύνολα Uα ενός ανοικτού καλύμματος της M και (β) για τη συρραφή αντικειμένων που ορίζονται στα ανοικτά σύνολα Uα, για την κατασκευή ενός ολικού αντικειμένου που να ορίζεται σε ολόκληρη την πολλαπλότητα.
΄Εστω ℝ* = ℝ \{0} και f : M → ℝ μια συνάρτηση σε μια πολλαπλότητα M. Η υποστήριξη (support) της f ορίζεται ως η κλειστή θήκη (κλειστότητα) του υποσυνόλου της M στο οποίο η f δεν μηδενίζεται:
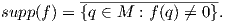
Ορισμός 4.2: ΄Εστω q ∈ M και U μια περιοχή του q. Μια συνάρτηση εξογκώματος στο q με υποστήριξη στο U (bump function at q supported in U) είναι μια συνεχής και μη αρνητική συνάρτηση ρ : M → ℝ, η οποία να παίρνει την τιμή 1 σε μια περιοχή του q και επιπλέον supp(ρ) ⊂ U.
Ενδιαφερόμαστε να κατασκευάσουμε συναρτήσεις εξογκώματος σε μια πολλαπλότητα M οι οποίες να είναι λείες και αυτό θα γίνει σε διαδοχικά βήματα.
Βήμα 1. Θεωρούμε τη διαφορίσιμη συνάρτηση f : ℝ → ℝ, με τιμή
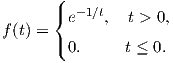
Βήμα 2. ΄Εστω g : ℝ → ℝ η συνάρτηση με τιμή
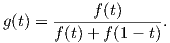 | (4.3) |
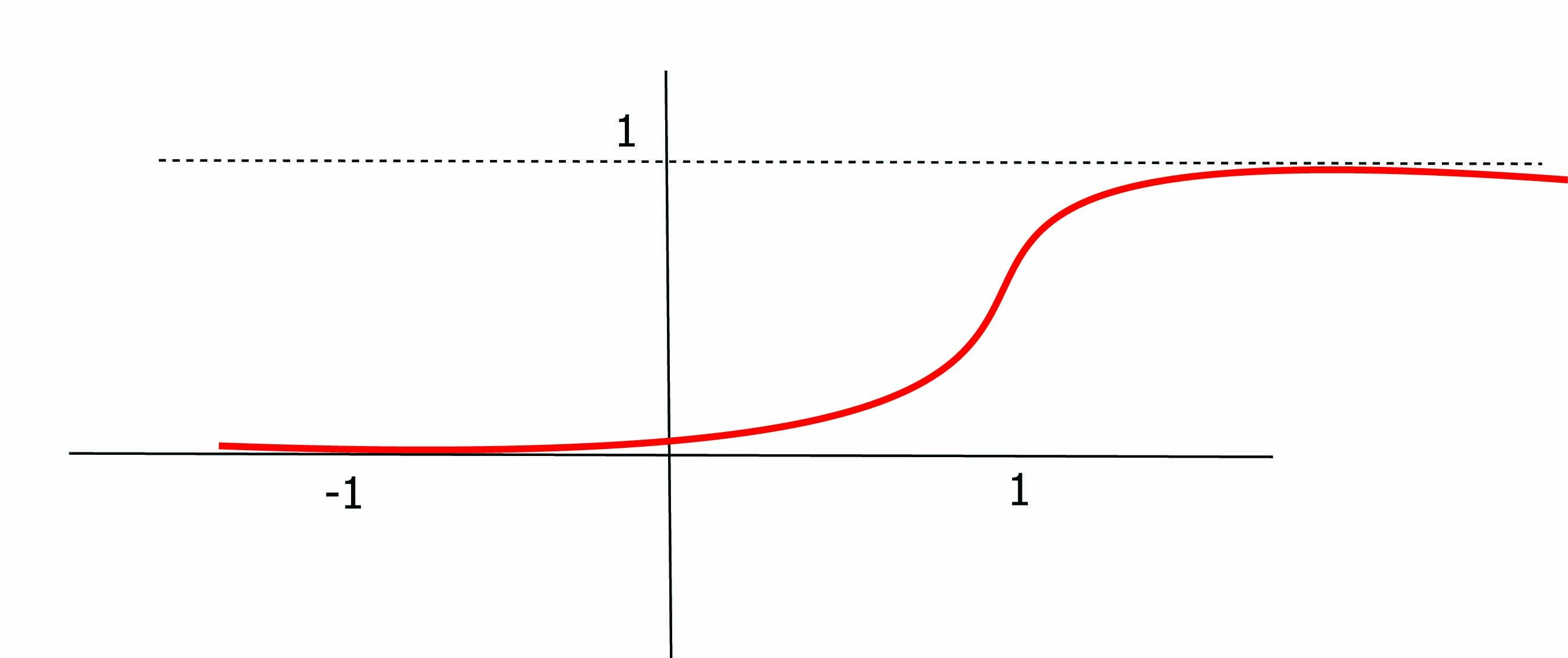
Ο παρονομαστής της παραπάνω συνάρτησης είναι πάντα μη μηδενικός, άρα η συνάρτηση g(t) ορίζεται για κάθε t. Πράγματι, αν t > 0 τότε f(t) > 0, συνεπώς
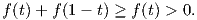
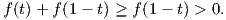
Εάν t ≤ 0 ο αριθμητής f(t) είναι ταυτοτικά μηδέν, άρα η g(t) είναι ταυτοτικά μηδέν. Εάν t ≥ 1 τότε 1 - t ≤ 0, άρα f(1 - t) = 0, οπότε g(t) = f(t)∕f(t) ≡ 1. Τελικά, η συνάρτηση g(t) έχει την ιδιότητα
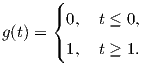
Βήμα 3. Δοθέντων δύο θετικών πραγματικών αριθμών a < b θα κατασκευάσουμε μια λεία συνάρτηση εξογκώματος ρ(x) στο 0 η οποία θα είναι ταυτοτικά μηδέν στο ανοικτό διάστημα [-a,a] με υποστήριξη στο διάστημα [-b,b]. Κάνουμε αρχικά μια γραμμική αλλαγή μεταβλητής, ώστε το διάστημα [a2,b2] να απεικονίζεται στο [0,1] ως εξής:
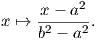
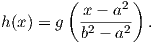
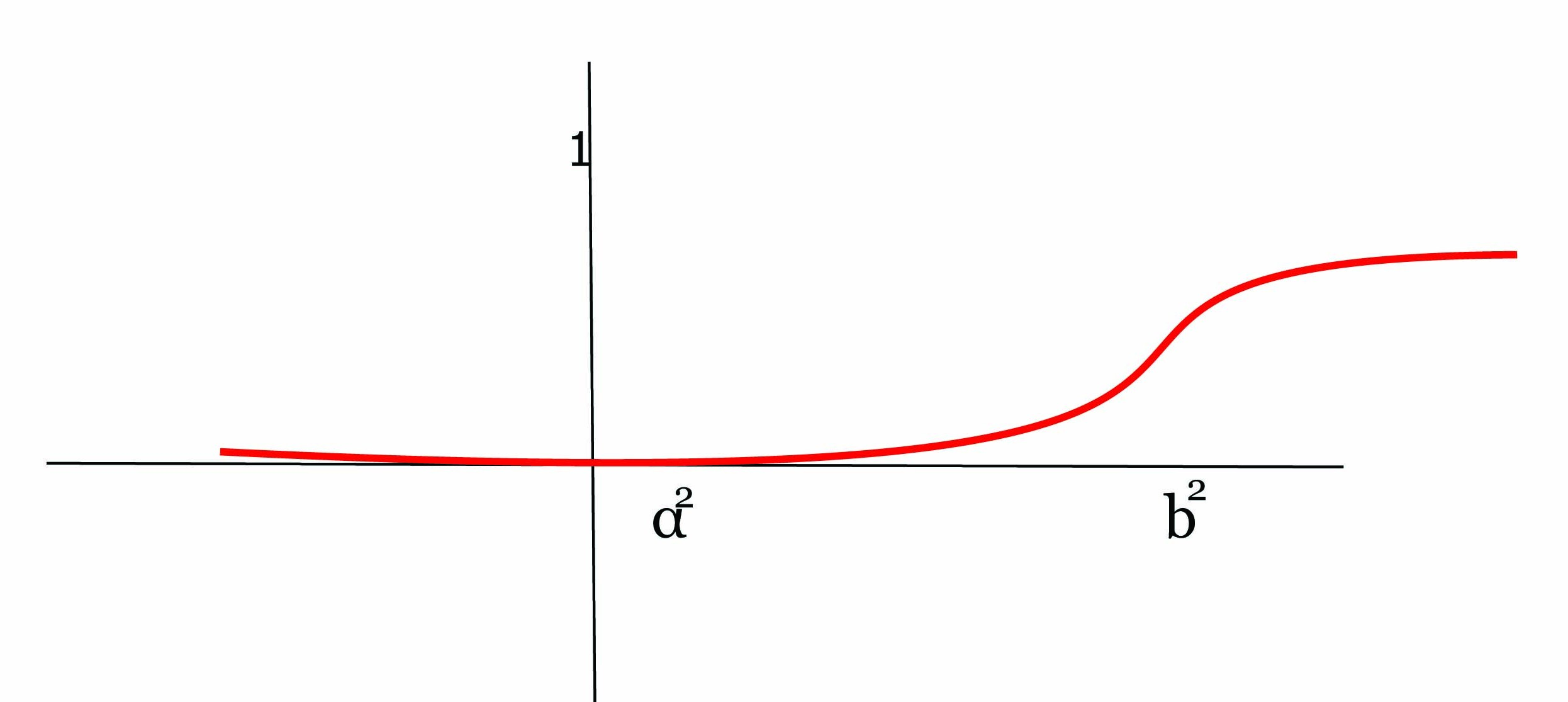
Τότε η συνάρτηση h : ℝ → [0,1] είναι διαφορίσιμη και έχει την ιδιότητα
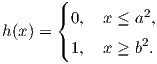
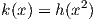
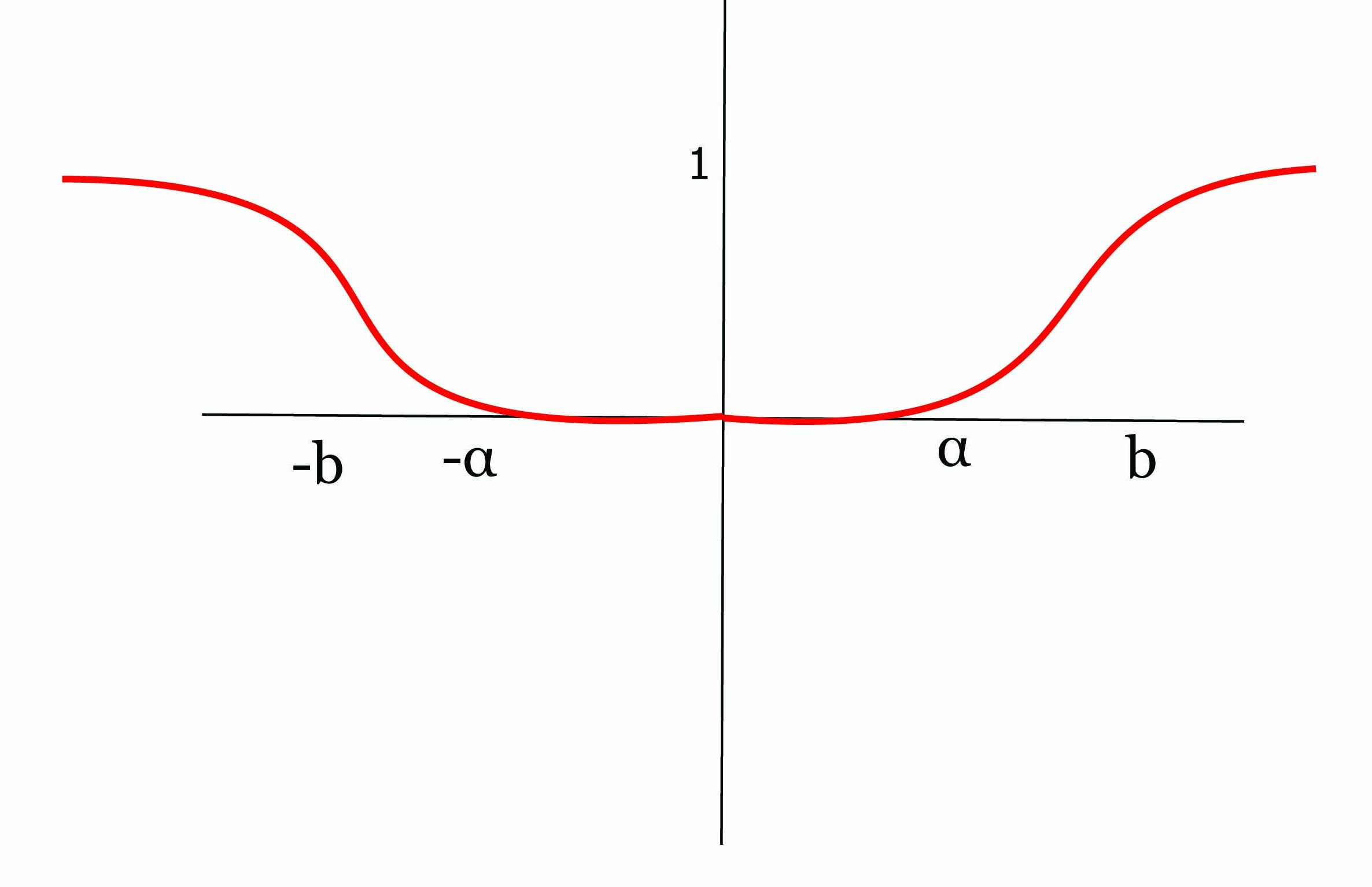
και τελικά θέτουμε
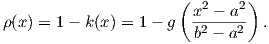
Η παραπάνω συνάρτηση ρ(x) είναι η επιθυμητή λεία συνάρτηση εξογκώματος στο 0. Αν τώρα q είναι ένας οποιοσδήποτε πραγματικός αριθμός, τότε η συνάρτηση ρ(x-q) είναι μια λεία συνάρτηση εξογκώματος στο σημείο q.
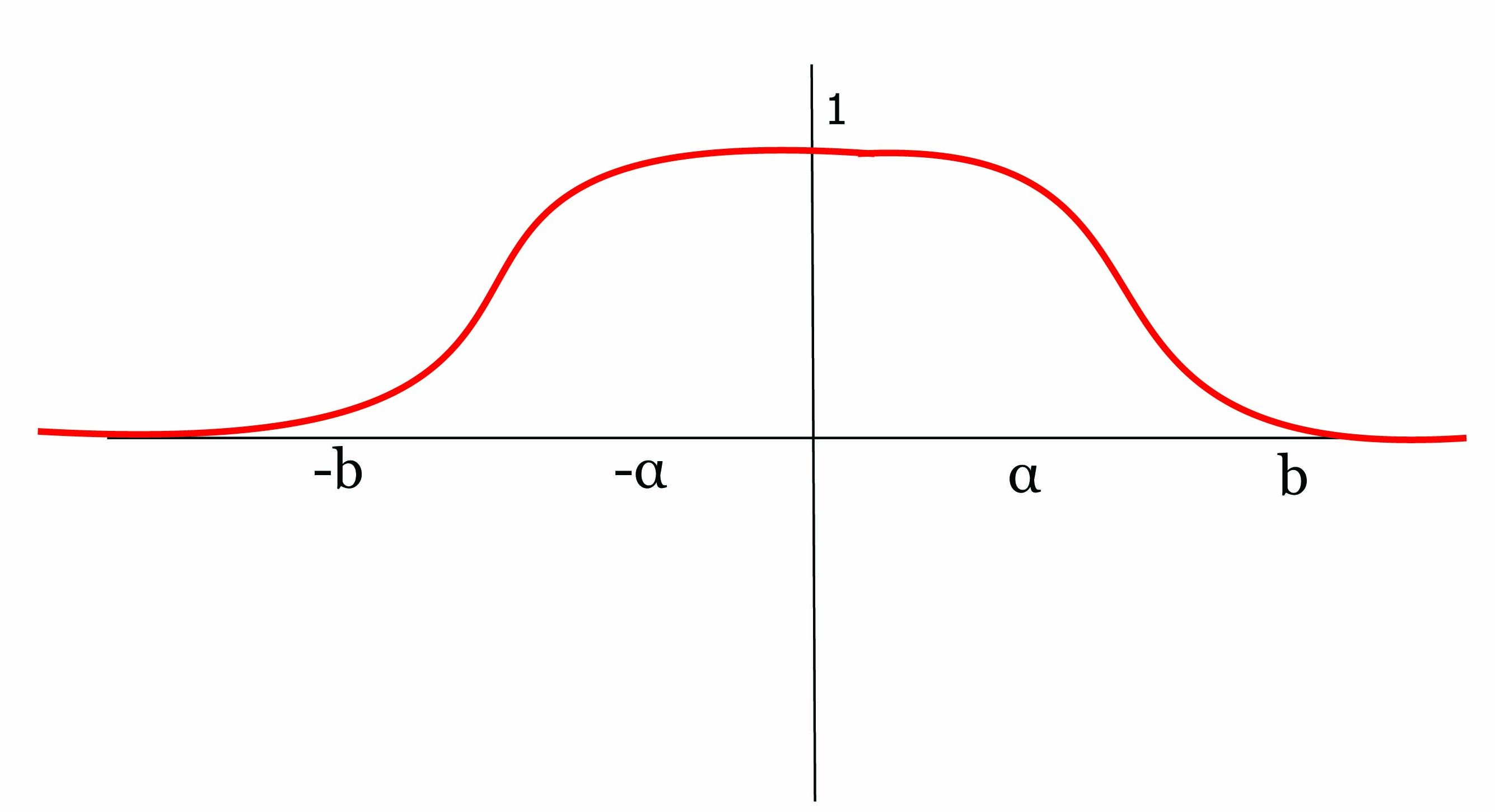
Βήμα 4. Στο βήμα αυτό θα επεκτείνουμε την κατασκευή της συναρτησης εξογκώματος από το ℝ στον ℝn. Για x ∈ ℝn θέτουμε
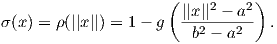
Γενικά μια λεία συνάρτηση εξογκώματος ορισμένη σε ένα ανοικτό υποσύνολο U μιας πολλαπλότητας M δεν επεκτείνεται σε μια λεία συνάρτηση στην M. ΄Ενα παράδειγμα είναι η συνάρτηση sec(x) στο ανοικτό διάστημα (-π∕2,π∕2) της πραγματικής ευθείας. Παρόλα αυτά, μια τέτοια επέκταση υπάρχει, εάν απαιτήσουμε η υπό κατασκευή συνάρτηση στην M να συμφωνεί με τη δοθείσα συνάρτηση σε μια περιοχή ενός σημείου στο U. Το τελικό αποτέλεσμα είναι το εξής:
Θεώρημα 4.1: (Θεώρημα λείας επέκτασης συνάρτησης). ΄Εστω f μια λεία συνάρτηση ορισμένη σε μια
περιοχή U ενός σημείου p μιας πολλαπλότητας M. Τότε υπάρχει μια λεία συνάρτηση 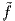 ορισμένη στην M
η οποία να παίρνει τις ίδιες τιμές με την f σε μια (ενδεχομένως μικρότερη) περιοχή του σημείου p.
ορισμένη στην M
η οποία να παίρνει τις ίδιες τιμές με την f σε μια (ενδεχομένως μικρότερη) περιοχή του σημείου p.
Απόδειξη. ΄Εστω ρ : M → ℝ μια λεία συνάρτηση εξογκώματος με υποστήριξη στο U, η οποία να είναι ταυτοτικά 1 σε μια περιοχή V του p. Ορίζουμε τη συνάρτηση
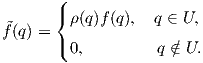
 της λείας συνάρτησης f μέσω της συνάρτησης εξογκώματος ρ.
της λείας συνάρτησης f μέσω της συνάρτησης εξογκώματος ρ. Η συνάρτηση 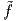 είναι λεία για κάθε q ∈ U ως γινόμενο λείων συναρτήσεων στο U. Αν q
είναι λεία για κάθε q ∈ U ως γινόμενο λείων συναρτήσεων στο U. Αν q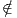 U
τότε q
U
τότε q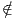 suppρ, άρα υπάρχει ένα ανοικτό σύνολο που να περιέχει το σημείο q και στο οποίο η
suppρ, άρα υπάρχει ένα ανοικτό σύνολο που να περιέχει το σημείο q και στο οποίο η 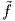 να
είναι ταυτοτικά 0 (επειδή το σύνολο suppρ είναι κλειστό). ΄Αρα τελικά η συνάρτηση
να
είναι ταυτοτικά 0 (επειδή το σύνολο suppρ είναι κλειστό). ΄Αρα τελικά η συνάρτηση 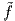 είναι λεία και
σε κάθε σημείο q
είναι λεία και
σε κάθε σημείο q U. Τέλος, επειδή ρ ≡ 1 στο V , η συνάρτηση
U. Τέλος, επειδή ρ ≡ 1 στο V , η συνάρτηση 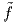 θα συμφωνεί με την f στο V .
▄
θα συμφωνεί με την f στο V .
▄
΄Εστω {Ui}i∈I ένα ανοικτό κάλυμμα μιας πολλαπλότητας M. Μια διαμέριση της μονάδας υποκείμενη στο {Ui}i∈I (partition of unity subordinate to {Ui}i∈I) είναι μια συλλογή από μη αρνητικές λείες συναρτήσεις {ρi : M → ℝ}i∈I που να ικανοποιούν suppρi ⊂ Ui και
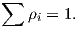
Μια συλλογή υποσυνόλων {Aα} ενός τοπολογικού χώρου S ονομάζεται τοπικά πεπερασμένη (locally finite) εάν κάθε σημείο q ∈ S έχει μια περιοχή η οποία να τέμνει μόνο πεπερασμένο αριθμό συνόλων Aα. Ειδικότερα, κάθε q ∈ S ανήκει σε πεπερασμένο μόνο αριθμό συνόλων Aα.
Παράδειγμα. ΄Εστω Ur,n = (r -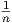 ,r +
,r + 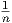 ) ⊂ ℝ. Τότε το σύνολο {Ur,n : r ∈ ℚ,n ∈ ℤ+} αποτελεί ένα ανοικτό
κάλυμμα του ℝ το οποίο δεν είναι τοπικά πεπερασμένο.
) ⊂ ℝ. Τότε το σύνολο {Ur,n : r ∈ ℚ,n ∈ ℤ+} αποτελεί ένα ανοικτό
κάλυμμα του ℝ το οποίο δεν είναι τοπικά πεπερασμένο.
Ορισμός 4.3: Μια λεία διαμέριση της μονάδας (partition of unity) επί μας πολλαπλότητας M είναι μια συλλογή από μη αρνητικές λείες συναρτήσεις {ρα : M → ℝ}α∈A, έτσι ώστε:
(i) Η οικογένεια των συνόλων {suppρα}α∈A να είναι τοπικά πεπερασμένη,
(ii) ∑ ρα = 1.
Αν {Uα}α∈A είναι ένα ανοικτό κάλυμμα της M, τότε η διαμέριση της μονάδας {ρα}α∈A ονομάζεται υποκείμενη (subordinate) στο ανοικτό κάλυμμα {Uα} εάν suppρα ⊂ Uα για κάθε α ∈ A.
Λόγω της ιδιότητας (i) κάθε σημείο q ∈ M ανήκει σε πεπερασμένο μόνο αριθμό συνόλων suppρα, άρα ρα(q)≠0 για πεπερασμένο μόνο αριθμό δεικτών α. Από αυτό προκύπτει ότι το άθροισμα της ιδιότητας (ii) σε κάθε σημείο της M είναι πεπερασμένο.
Παράδειγμα. ΄Εστω U = (-∞,2) και V = (-1,∞) ανοικτά διαστήματα της πραγματικής ευθείας. ΄Εστω ρV μια λεία συνάρτηση της μορφής (4.3) και ρU = 1 - ρV . Τότε suppρV ⊂ V και suppρU ⊂ U, άρα το ζεύγος {ρU,ρV } αποτελεί μια διαμέριση της μονάδας υποκείμενη στο ανοικτό κάλυμμα {U,V } του ℝ.
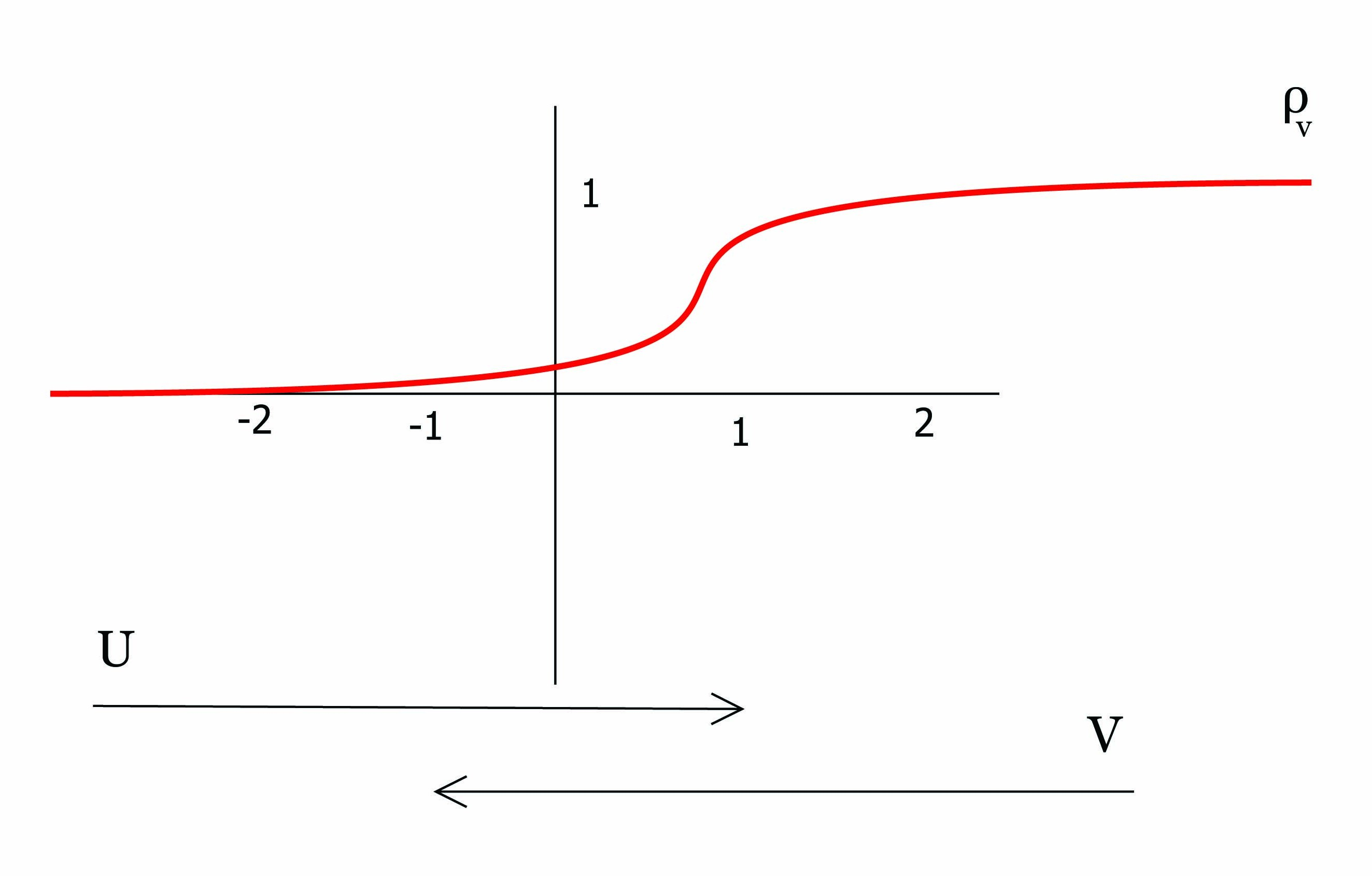
Η ύπαρξη μιας λείας διαμέρισης της μονάδας εξασφαλίζεται από το παρακάτω θεώρημα, η απόδειξη του οποίου είναι ιδιαίτερα τεχνική και παραλείπεται.
Θεώρημα 4.2: (΄ϒπαρξης λείας διαμέρισης της μονάδας). ΄Εστω {Uα}α ένα ανοικτό κάλυμμα μιας πολλαπλότητας M. Τότε
(i) ϒπάρχει μια λεία διαμέριση της μονάδας {ρk}k=1∞, έτσι ώστε κάθε συνάρτηση ρk να έχει συμπαγή υποστήριξη και για κάθε k να ισχύει suppρk ⊂ Uα, για κάποιο α ∈ A.
(ii) Αν δεν απαιτήσουμε τη συμπαγή υποστήριξη, τότε υπάρχει μια λεία διαμέριση της μονάδας {ρα} υποκείμενη του καλύμματος {Uα}.
Η έννοια του διανυσματικού πεδίου εμφανίζεται τακτικά στη φύση, για παράδειγμα ως το πεδίο ταχύτητας της ροής ενός υγρού, το ηλεκτρικό πεδίο ενός φορτίου, το βαρυτικό πεδίο μιας μάζας, κ.ά. Για την περίπτωση των πολλαπλοτήτων, μας ενδιαφέρουν τα λεία (διαφορίσιμα) διανυσματικά πεδία. Κάθε λείο διανυσματικό πεδίο παράγει τοπικά μια οικογένεια καμπυλών, οι οποίες ονομάζονται ολοκληρωτικές καμπύλες. Το διάνυσμα ταχύτητας μιας ολοκληρωτικής καμπύλης ισούται με τον περιορισμό του διανυσματικού πεδίου στην καμπύλη. Η εύρεση μιας ολοκληρωτικής καμπύλης που να διέρχεται από ένα σημείο ισοδυναμεί με την επίλυση ενός συστήματος συνήθων διαφορικών εξισώσεων με αρχικές συνθήκες. Επίσης, το σύνολο όλων των λείων διανυσματικών πεδιων σε μια πολλαπλότητα, πέραν της δομής του ως διανυσματικός χώρος, έχει και δομή μιας άλγεβρας Lie την οποία και θα εξετάσουμε.
Ορισμός 4.4: ΄Ενα διανυσματικό πεδίο X σε μια πολλαπλότητα M είναι μια απεικόνιση η οποία σε κάθε σημείο p ∈ M αντιστοιχεί ένα εφαπτόμενο διάνυσμα Xp ∈ TpM. Εναλλακτικά, ένα διανυσματικό πεδίο είναι μια τομή X : M → TM στην εφαπτόμενη δέσμη π : TM → M. Το X ονομάζεται λείο (ή διαφορίσιμο) εάν η απεικόνιση X : M → TM είναι λεία.
Συμβολίζουμε με X(M) το σύνολο όλων των λείων διανυσματικών πεδίων στην πολλαπλότητα M.
΄Εστω (U;x1,…,xn) ένας τοπικός χάρτης της M. Τότε η τιμή ενός διανυσματικού πεδιου X σε ένα σημείο p ∈ U δίνεται ως
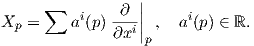
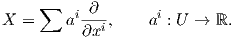
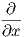 + x
+ x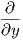 στον ℝ2.
στον ℝ2.Χρησιμοποιώντας τη διαφορική δομή της εφαπτόμενης δέσμης TM προκύπτει ότι το παραπάνω διανυσματικό πεδίο είναι λείο εάν και μόνο εάν οι συναρτήσεις ai είναι λείες στο U.
΄Εστω F(M) το σύνολο όλων των λείων συναρτήσεων στη M. Για f ∈ F(M) και X ∈ X(M) ορίζεται η συνάρτηση Xf : M → ℝ με τιμή
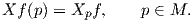
Πρόταση 4.1: ΄Ενα διανυσματικό πεδίο X σε μια πολλαπλότητα M είναι λείο, εάν και μόνο εάν για κάθε λεία συνάρτηση f στην M, η συνάρτηση Xf είναι λεία.
Απόδειξη. ΄Εστω X ∈ X(M), f ∈ F(M) και (U;x1,…,xn) ένας τοπικός χάρτης της M. Τότε το X
εκφράζεται ως X = ∑
ai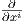 , όπου οι συναρτήσεις ai είναι λείες, άρα η συνάρτηση Xf = ∑
ai
, όπου οι συναρτήσεις ai είναι λείες, άρα η συνάρτηση Xf = ∑
ai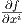 είναι
λεία στο U. Επειδή η πολλαπλότητα M καλύπτεται με μια συλλογή χαρτών, η συνάρτηση Xf είναι λεία
στην M.
είναι
λεία στο U. Επειδή η πολλαπλότητα M καλύπτεται με μια συλλογή χαρτών, η συνάρτηση Xf είναι λεία
στην M.
Αντίστροφα, έστω (U;x1,…,xn) ένας τοπικός χάρτης της M. Τότε στο U το πεδίο X εκφράζεται ως
X = ∑
ai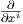 . ΄Εστω p ∈ U. Χρησιμοποιώντας το Θεώρημα 4.1 κάθε συνάρτηση συντεταγμένων xk
(i = 1,…,k), μπορεί να επεκταθεί σε μια λεία συνάρτηση
. ΄Εστω p ∈ U. Χρησιμοποιώντας το Θεώρημα 4.1 κάθε συνάρτηση συντεταγμένων xk
(i = 1,…,k), μπορεί να επεκταθεί σε μια λεία συνάρτηση 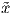 k σε ολόκληρη την πολλαπλότητα M, η οποία να
συμφωνεί με τη xk σε μια περιοχή V ⊂ U του p. Τότε στην V το πεδίο X εκφράζεται ως
k σε ολόκληρη την πολλαπλότητα M, η οποία να
συμφωνεί με τη xk σε μια περιοχή V ⊂ U του p. Τότε στην V το πεδίο X εκφράζεται ως
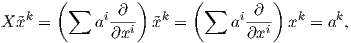
΄Ενα λείο διανυσματικό πεδίο X σε μια πολλαπλότητα M μπορεί να θεωρηθεί και ως ένας γραμμικός τελεστής X : F(M) → F(M), ο οποίος να είναι μια παραγώγιση, δηλαδή ισχύει
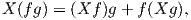
Πρόταση 4.2: ΄Εστω X ένα λείο διανυσματικό πεδίο ορισμένο σε μια περιοχή U ενός σημείου p σε μια
πολλαπλότητα M. Τότε υπάρχει ένα λείο διανυσματικό πεδίο 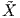 το οποίο αποτελεί επέκταση του X και
ορίζεται σε μια (ενδεχομένως μικρότερη) περιοχή του σημείου p.
το οποίο αποτελεί επέκταση του X και
ορίζεται σε μια (ενδεχομένως μικρότερη) περιοχή του σημείου p.
Απόδειξη. Επιλέγουμε μια λεία συνάρτηση εξογκώματος ρ : M → ℝ με υποστήριξη στο U και η οποία
να είναι ταυτοτικά 1 σε μια περιοχή V του σημείου p. Τότε η ζητούμενη συνάρτηση επέκτασης είναι η
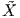 : M → ℝ με τιμή
: M → ℝ με τιμή
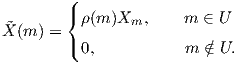
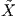 είναι λεία ως γινόμενο δύο λείων συναρτήσεων. Το ότι είναι επέκταση της X προκύπτει
όπως στην απόδειξη του Θεωρήματος 4.1. ▄
είναι λεία ως γινόμενο δύο λείων συναρτήσεων. Το ότι είναι επέκταση της X προκύπτει
όπως στην απόδειξη του Θεωρήματος 4.1. ▄
Εάν N είναι μια υποπολλαπλότητα της πολλαπλότητας M, τότε υπάρχει η εξής χρήσιμη έννοια διανυσματικού πεδίου:
Ορισμός 4.5: ΄Εστω N μια κανονική υποπολλαπλότητα της πολλαπλότητας M. ΄Ενα διανυσματικό πεδίο X της M κατά μήκος (along) της N είναι μια απεικόνιση η οποία αντιστοιχίζει σε κάθε σημείο p ∈ N ένα εφαπτόμενο διάνυσμα Xp ∈ TpM. ΄Ενα διανυσματικό πεδίο X κατά μήκος της N ονομάζεται λείο εάν για κάθε λεία συνάρτηση f ∈ F(M) η συνάρτηση fX είναι λεία συνάρτηση της N.
Παράδειγμα. ΄Εστω N μια κανονική επιφάνεια στον ℝ3. Τότε ένα κάθετο διανυσματικό πεδίο της επιφάνειας N είναι ένα διανυσματικό πεδίο κατά μήκος της N στον ℝ3, αλλά όχι ένα διανυσματικό πεδίο στην N.
Παρατήρηση. Προσέξτε τη διαφορά στις έννοιες διανυσματικό πεδίο σε μια πολλαπλότητα ή επί μιας πολλαπλότητας, δηλαδή μια απεικόνιση X : M → TM και διανυσματικό πεδίο κατά μήκος μιας (υπο)πολλαπλότητας, δηλαδή απεικόνιση X : N → TM.
Μια ολοκληρωτική καμπύλη ενός λείου διανυσματικού πεδίου είναι μια λεία καμπύλη της οποίας το εφαπτόμενο διάνυσμα σε κάθε σημείο της ισούται με την τιμή του διανυσματικού πεδίου στο σημείο αυτό.
Ορισμός 4.6: ΄Εστω X ένα λείο διανυσματικό πεδίο σε μια πολλαπλότητα M και έστω p ∈ M. Μια ολοκληρωτική καμπύλη integral curve του X είναι μια λεία καμπύλη γ : (a,b) → M τέτοια ώστε γ′(t) = Xγ(t) για κάθε t ∈ (a,b). ϒποθέτουμε συνήθως ότι το ανοικτό διάστημα (a,b) περιέχει το 0. Τότε αν γ(0) = p θα λέμε ότι η ολοκληρωτική καμπύλη έχει αρχή το p. Προκειμένου να τονίσομε την εξάρτηση μιας τέτοιας ολοκληρωτικής καμπύλης από το σημείο p, θα γράφουμε γt(p) (αντί γ(t)).
Μια ολοκληρωτική καμπύλη ονομάζεται μεγιστική (maximal), εάν το πεδίο ορισμού της δεν μπορεί να επεκταθεί σε ένα μεγαλύτερο διάστημα.
Παραδείγματα.
1. Θεωρούμε το διανυσματικό πεδίο X = -y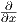 + x
+ x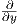 του ℝ2. Αναζητάμε μια ολοκληρωτική καμπύλη γ του X με
αρχή το σημείο p = (x0,y0) ∈ ℝ2. Η καμπύλη γ(t) = (x(t),y(t)) είναι μια ολοκληρωτική καμπύλη του X εάν και
μόνο εάν ισχύει γ′(t) = Xγ(t). Ισοδύναμα, προκύπτει η σχέση
του ℝ2. Αναζητάμε μια ολοκληρωτική καμπύλη γ του X με
αρχή το σημείο p = (x0,y0) ∈ ℝ2. Η καμπύλη γ(t) = (x(t),y(t)) είναι μια ολοκληρωτική καμπύλη του X εάν και
μόνο εάν ισχύει γ′(t) = Xγ(t). Ισοδύναμα, προκύπτει η σχέση
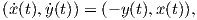

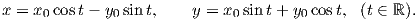
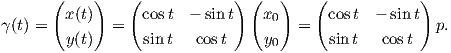
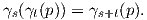
΄Εστω Diff(M) η ομάδα όλων των αμφιδιαφορίσεων της πολλαπλότητας M (με πράξη τη σύνθεση απεικονίσεων). Τότε ένας ομομορφισμός
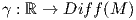
2. Θα βρούμε τη μεγιστική ολοκληρωτική καμπύλη του διανυσματικού πεδίου X = x2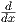 του ℝ με αρχή το
x = 3. Αν x(t) είναι η ζητούμενη ολοκληρωτική καμπύλη, τότε η εξίσωση x′(t) = Xx(t) ισοδυναμεί με
την
του ℝ με αρχή το
x = 3. Αν x(t) είναι η ζητούμενη ολοκληρωτική καμπύλη, τότε η εξίσωση x′(t) = Xx(t) ισοδυναμεί με
την
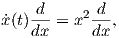
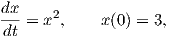
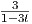 . Το μέγιστο διάστημα στο οποίο ορίζεται η ολοκληρωτική καμπύλη αυτή και το
οποίο περιέχει το 0 είναι το (-∞,1∕3).
. Το μέγιστο διάστημα στο οποίο ορίζεται η ολοκληρωτική καμπύλη αυτή και το
οποίο περιέχει το 0 είναι το (-∞,1∕3).
Βλέπουμε λοιπόν ότι για να βρούμε τοπικά μια ολοκληρωτική καμπύλη, αρκεί να λύσουμε ένα σύστημα συνήθων
διαφορικών εξισώσεων με αρχικές συνθήκες. Ας το δούμε αυτό γενικά.
Θα βρούμε μια ολοκληρωτική καμπύλη γ(t) ενός λείου διανυσματικού πεδίου X σε μια πολλαπλότητα M, με αρχή
ένα σημείο p ∈ M. Αρχικά επιλέγουμε έναν τοπικό χάρτη (U,φ) = (U;x1,…,xn) στο σημείο p. Τότε το
διανυσματικό πεδίο εκφράζεται τοπικά ως
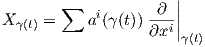
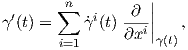
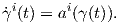
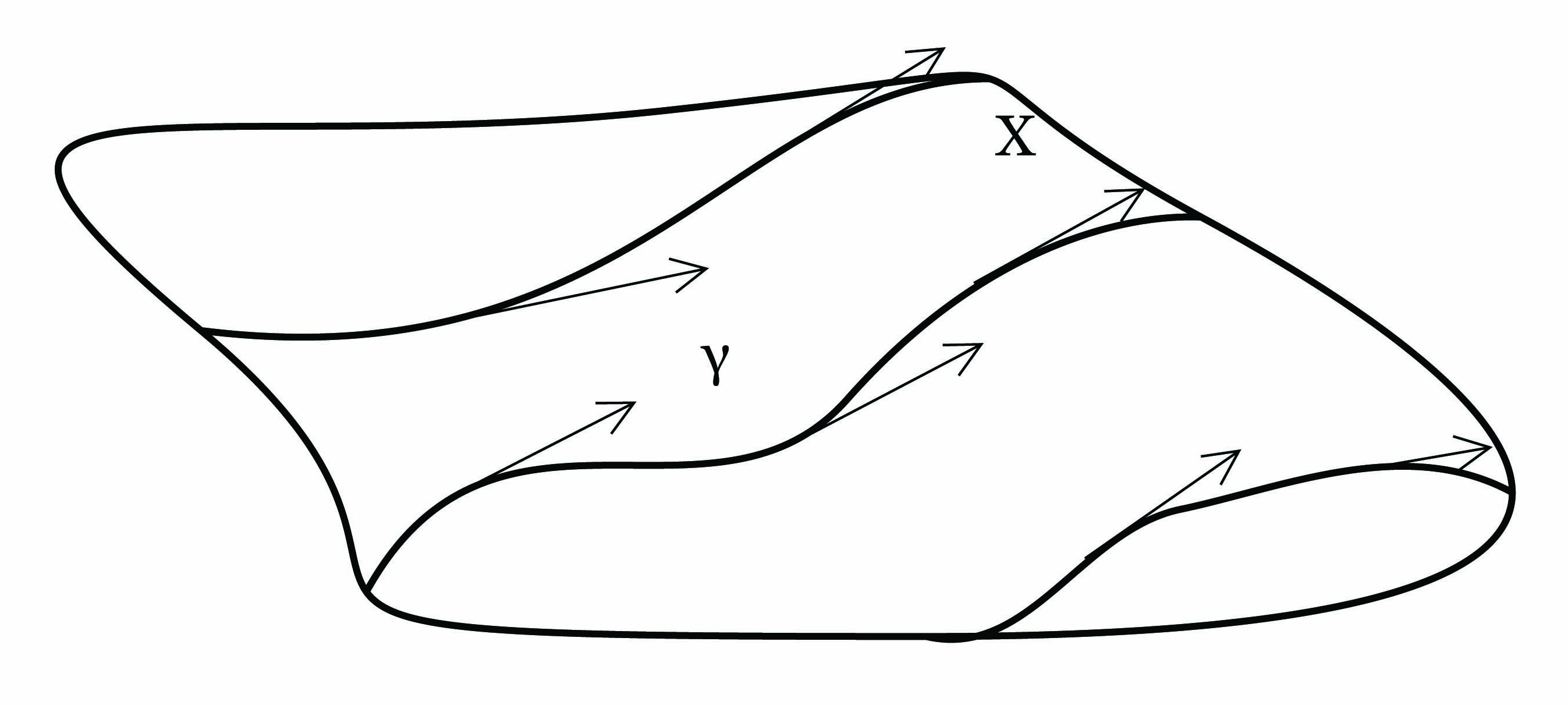
Θεώρημα 4.3: ΄Εστω V ένα ανοικτό υποσύνολο του ℝn, p0 ∈ V και f : V → ℝn μια διαφορίσιμη συνάρτηση. Τότε το πρόβλημα αρχικών τιμών
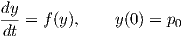
Λόγω του θεωρήματος αυτού εξασφαλίζεται η ύπαρξη και η μοναδικότητα μιας μέγιστης ολοκληρωτικής καμπύλης ενός λείου διανυσματικού πεδίου X, η οποία έχει αρχή ένα σημείο p σε έναν χάρτη U μιας πολλαπλότητας M.
Θα μελετήσουμε την εξάρτηση μιας ολοκληρωτικής καμπύλης από την αρχή, δηλαδή από το σημείο που διέρχεται. Η μελέτη του προβλήματος θα γίνει πάλι τοπικά. Η συνάρτηση y στο Θεώρημα 4.3 θα εξαρτάται τώρα από δύο μεταβλητές t και q και η συνθήκη, ώστε η y να είναι μια ολοκληρωτική καμπύλη με αρχή το σημείο q, θα λάβει την μορφή
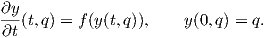
Θεώρημα 4.4: ΄Εστω V ένα ανοικτό υποσύνολο του ℝn και f : V → ℝn μια διαφορίσιμη συνάρτηση. Τότε για κάθε σημείο p ∈ V υπάρχουν μια περιοχή W ⊂ V του p, αριθμός ε > 0 και διαφορίσιμη συνάρτηση y : (-ε,ε) × W → V ώστε να ισχύει
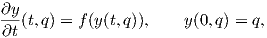
Εφαρμόζουμε το παραπάνω θεώρημα για ένα λείο διανυσματικό πεδίο X σε έναν χάρτη U που περιέχει το σημείο p. Τότε υπάρχουν μια περιοχή W ⊂ U του p, ε > 0 και λεία συνάρτηση
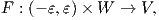
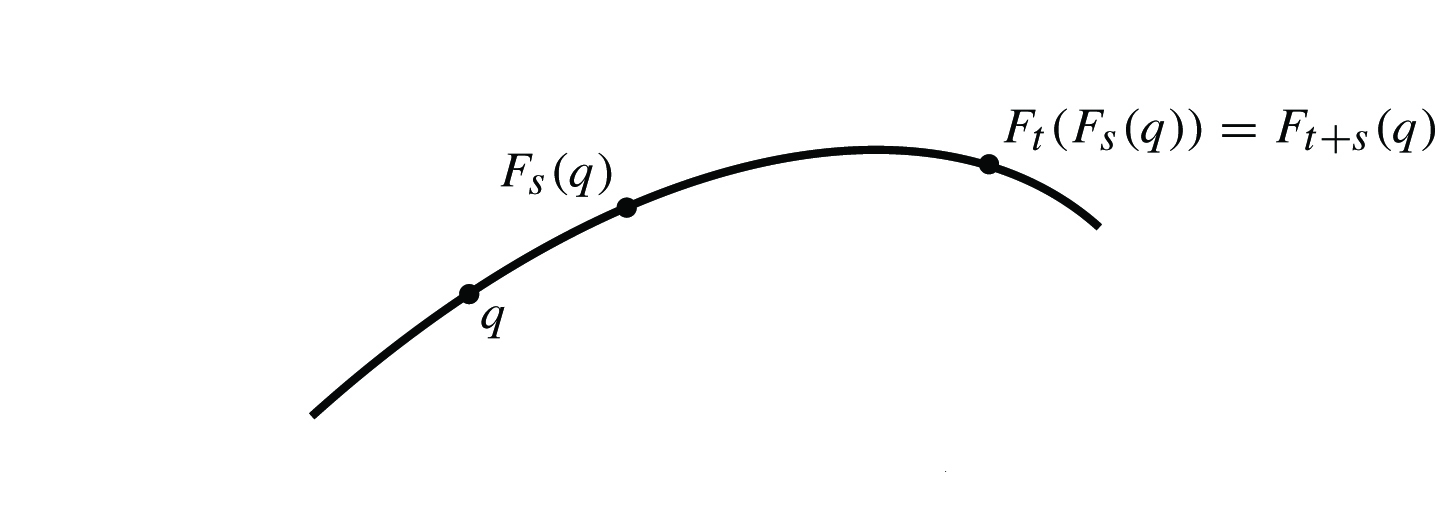
Ας υποθέσουμε ότι για t,s ∈ (-ε,ε) ορίζονται οι τιμές Ft(Fs(q)) και Ft+s(q). Τότε ως συναρτήσεις του t, οι Ft(Fs(q)) και Ft+s(q) αποτελούν ολοκληρωτικές καμπύλες του πεδίου X με αρχή το σημείο Fs(q) (για t = 0), άρα λόγω της μοναδικότητας της λύσης μιας ολοκληρωτικής καμπύλης που διέρχεται από δοθέν σημείο, προκύπτει ότι
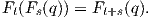
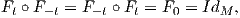
Ορισμός 4.7: Μια τοπική ροή γύρω από ένα σημείο p ενός ανοικτού υποσυνόλου U μιας πολλαπλότητας, είναι μια λεία συνάρτηση
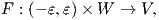
(i) F0(q) = q για κάθε q ∈ W,
(ii) Ft(Fs(q)) = Ft+s(q), υπό την προϋπόθεση ότι ορίζονται και τα δύο μέλη της ισότητας.
Εάν F(t,q) είναι μια τοπική ροή ενός διανυσματικού πεδίου X στο ανοικτό σύνολο U, τότε ισχύει
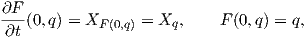
Παράδειγμα. Η συνάρτηση F : ℝ × ℝ2 → ℝ2 με F(t,(x,y)) = (cost x- sint y,sint x + cost y) είναι μια ολική ροή στον ℝ2. Η ροή αυτή ορίζει το διανυσματικό πεδίο
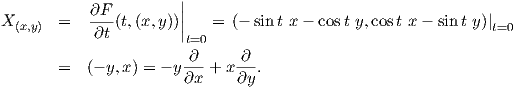
΄Εστω X,Y δύο λεία διανυσματικά πεδία ορισμένα σε ένα ανοικτό υποσύνολο U μιας πολλαπλότητας M, τα οποία τα θεωρούμε ως παραγωγίσεις στην άλγεβρα F(U). Αν f είναι μια λεία συνάρτηση στο U, τότε λόγω της Πρότασης 4.1 η συνάρτηση Y f είναι λεία στο U και για τον ίδιο λόγο η συνάρτηση (XY )(f) := X(Y f) είναι επίσης λεία στο U. Αν και λόγω της ℝ-γραμμικότητας των X,Y η συνάρτηση XY : F(U) → F(U) είναι και αυτή ℝ γραμμική, δεν ικανοποιεί τον κανόνα του Leibnitz, άρα δεν είναι παραγώγιση (άρα ούτε και διανυσματικό πεδίο). Παρόλα αυτά, η διαφορά XY - Y X είναι μια παραγώγιση στο U, άρα ορίζει ένα διανυσματικό πεδίο, το οποίο ονομάζεται γινόμενο Lie των X και Y .
Ορισμός 4.8: ΄Εστω X,Y δύο λεία διανυσματικά πεδία ορισμένα σε ένα ανοικτό υποσύνολο U μιας πολλαπλότητας M και έστω p ∈ U. Το γινόμενο Lie των X και Y είναι το διανυσματικό πεδίο [X,Y ] του οποίου η τιμή στο σημείο p ορίζεται ως εξής: Για κάθε σπόρο f μιας λείας συνάρτησης στο σημείο p είναι
 = X (Y f)- Y (Xf ).
p p p](02_chapter_0489x.png) | (4.4) |
Η ποσότητα [X,Y ]p είναι μια παραγώγιση στο p, άρα ορίζει ένα εφαπτόμενο διάνυσμα στο σημείο p. Καθώς το p μεταβάλλεται στο U το [X,Y ] ορίζει ένα διανυσματικό πεδίο στο U.
Εάν τα X και Y είναι λεία διανυσματικά πεδία στην πολλαπλότητα M, τότε και το γινόμενο Lie [X,Y ] είναι ένα λείο διανυσματικό πεδίο στη M. Πράγματι, έστω f ∈ X(M). Τότε λόγω της Πρότασης 4.1 οι συναρτήσεις Xf και Y f είναι λείες, άρα και η συνάρτηση
![[X, Y ]f = X (Y f)- Y (Xf )](02_chapter_0490x.png)
Από τα παραπάνω προκύπτει ότι το γινόμενο Lie ορίζει έναν τελεστή
![[ , ] : X (M ) × X (M ) → X (M )](02_chapter_0491x.png)
![[X, Y] = - [Y,X ],](02_chapter_0492x.png)
![[X, [Y,Z ]]+ [Y,[Z,X ]]+ [Z,[X,Y ]] = 0.](02_chapter_0493x.png) | (4.5) |
Οι ιδιότητες αυτές του γινομένου Lie ικανοποιούν μια σημαντική δομή σε έναν διανυσματικό χώρο, την άλγεβρα Lie.
Ορισμός 4.9: Μια άλγεβρα Lie επί ενός σώματος F είναι ένας διανυσματικός χώρος V επί του F εφοδιασμένος με ένα γινόμενο [ , ] : V × V → V (γινόμενο Lie - Lie bracket), το οποίο ικανοποιεί τις εξής ιδιότητες: για a,b ∈ F και X,Y,Z ∈ V , τότε
(i) [aX + bY,Z] = a[X,Z] + b[Y,Z]
[X,aY + bZ] = a[X,Y ] + b[X,Z] (διγραμμικότητα),
(ii) [Y,X] = -[X,Y ],
(iii) [X,[Y,Z]] + [Y,[Z,X]] + [Z,[X,Y ]] = 0 (ταυτότητα Jacobi).
Παραδείγματα.
1. Ο διανυσματικός χώρος X(M) όλων των λείων διανυσματικών πεδιων σε μια πολλαπλότητα M αποτελεί μια πραγματική άλγεβρα Lie, με γινόμενο Lie το γινόμενο Lie διανυσματικών πεδίων.
2. ΄Εστω Mn(F) ο διανυσματικός χώρος όλων των n × n πινάκων με στοιχεία από το σώμα F. Για κάθε X,Y ∈ Mn(F) η πράξη
![[X, Y] = XY - YX](02_chapter_0494x.png)
3. Αν (A,⋅) είναι μια άλγεβρα επί ενός σώματος F, τότε η πράξη
![[x,y ] = x ⋅y - y ⋅x](02_chapter_0495x.png)
Δύο διανυσματικά πεδία σε δύο πολλαπλότητες είναι δυνατόν να συσχετιστούν μέσω μιας λείας απεικόνισης με τον ακόλουθο τρόπο.
Ορισμός 4.10: ΄Εστω f : M → N μια λεία απεικόνιση μεταξύ πολλαπλοτήτων. ΄Ενα διανυσματικό πεδίο X στην M ονομάζεται f-συσχετισμένο (f-related) με ένα διανυσματικό πεδίο στη N, εάν για κάθε p ∈ M ισχύει
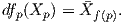
Παράδειγμα. ΄Εστω f : M → N μια αμφιδιαφόριση και X ένα διανυσματικό πεδίο στην πολλαπλότητα M. Επειδή η f είναι 1 - 1 και επί, ορίζεται καλώς το διανυσματικό πεδίο df(X) στην πολλαπλότητα N με τύπο df(X)f(p) = dfp(Xp) (p ∈ M). Τότε το διανυσματικό πεδίο X είναι f-συσχετισμένο με το διανυσματικό πεδίο df(X).
Η παρακάτω πρόταση δίνει μια ικανή και αναγκαία συνθήκη, ώστε δύο διανυσματικά πεδία να είναι f-συσχετισμένα.
Πρόταση 4.3: ΄Εστω f : M → N μια λεία απεικόνιση μεταξύ πολλαπλοτήτων. Δύο διανυσματικά πεδία X ∈ X(M) και ∈ X(N) είναι f-συσχετισμένα εάν και μόνο εάν για κάθε g ∈ F(N) ισχύει
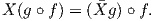
Απόδειξη. Για το ευθύ, υποθέτουμε ότι τα διανυσματικά πεδία X ∈ X(M) και ∈ X(N) είναι f-συσχετισμένα. ΄Εστω g ∈ F(N) και p ∈ M. Τότε θα ισχύει dfp(Xp)g = f(p)g και χρησιμοποιώντας τους ορισμούς του διαφορικού και του g προκύπτει ότι Xp(g∘f) = (g)(f(p)). Η σχέση αυτή ισοδυναμεί με τη (X(g ∘ f))(p) = (g)(f(p)). Επειδή η τελευταία ισότητα ισχύει για κάθε p ∈ M, προκύπτει ότι X(g ∘ f) = (g) ∘ f. Το αντίστροφο προκύπτει με αναστροφή των συλλογισμών. ▄
Πρόταση 4.4: ΄Εστω f : M → N μια λεία απεικόνιση μεταξύ πολλαπλοτήτων. Εάν τα διανυσματικά πεδία X και Y στην M είναι f-συσχετισμένα με τα και αντίστοιχα στη N, τότε το γινόμενο Lie [X,Y ] στην M είναι f-συσχετισμένο με το γινόμενο Lie [,] στην N.
Απόδειξη. ΄Εστω g ∈ F(N). Τότε από τον ορισμό του γινομένου Lie,των f-συσχετισμένων διανυσματικών πεδίων και της Πρότασης 4.3 έχουμε ότι
 = XY (g ∘ f)- Y X (g ∘ f)
? ?
= X ((Y g)∘f )- Y ((Xg ) ∘f)
= (X??Y g)∘ f - (Y?X?g )∘ f
= ((X??Y - ?Y ?X )g)∘f
= ([ ?X, ?Y]g)∘ f.](02_chapter_0498x.png)
1. ΄Εστω X και Y δύο λεία διανυσματικά πεδία σε μια πολλαπλότητα M. Αποδείξτε ότι X = Y εάν και μόνο εάν για κάθε λεία συνάρτηση f : M → ℝ ισχύει Xf = Y f.
2. ΄Εστω S2n-1 = {(x1,…,xn,y1,…,yn) ∈ ℝ2n : ∑ i=1n((xi)2 + (yi)2) = 1} η μοναδιαία σφαίρα στον ℝ2n. Αποδείξτε ότι το διανυσματικό πεδίο
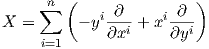
3. Βρείτε τη μεγιστική ολοκληρωτική καμπύλη του διανυσματικού πεδίου X = x2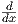 ∈ X(ℝ), η οποία διέρχεται
από το σημείο X(0) = x0. Είναι αυτό το διανυσματικό πεδίο πλήρες;
∈ X(ℝ), η οποία διέρχεται
από το σημείο X(0) = x0. Είναι αυτό το διανυσματικό πεδίο πλήρες;
4. Βρείτε τις ολοκληρωτικές καμπύλες του διανυσματικού πεδίου στον ℝ3
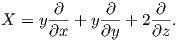
5. ΄Εστω γ : (a,b) → M μια ολοκληρωτική καμπύλη σε μια πολλαπλότητα M. Αποδείξτε ότι για κάθε s ∈ ℝ, η απεικόνιση
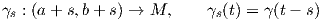
6. ϒπολογίστε το γινόμενο Lie των διανυσματικών πεδίων στον ℝ3
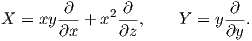
7. Αποδείξτε ότι η έκφραση (4.4) ορίζει μια παραγώγιση στο σύνολο Cp∞(U).
8. Αποδείξτε την ταυτότητα Jacobi (4.5) για διανυσματικά πεδία.
9. ΄Εστω (U;x1,…,xn) ένα τοπικό σύστημα συντεταγμένων μιας πολλαπλότητας M. Αποδείξτε ότι
![[-∂-,-∂--] = 0, (i,j = 1,...,n).
∂xi ∂xj](02_chapter_04104x.png)
10. ΄Εστω (U;x1,…,xn) ένα τοπικό σύστημα συντεταγμένων μιας πολλαπλότητας M και έστω
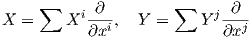
![∑ k-∂--
[X, Y] = [X, Y ]∂xk .](02_chapter_04106x.png)
11. Μια παραγώγιση σε μια άλγεβρα Lie V επί ενός σώματος F είναι ένας F-γραμμικός τελεστής D : V → V , ο οποίος ικανοποιεί την σχέση
![D [X,Y ] = [DX, Y]+ [X, DY ], για κάθε X,Y ∈ V.](02_chapter_04107x.png)
12. ΄Εστω M μια λεία πολλαπλότητα, f,g ∈ F(M) και X,Y ∈ X(M). Αποδείξτε ότι
![[f X,gY ] = f g[X, Y ]+ f(Xg )Y - g(Yf )X.](02_chapter_04108x.png)
13. ΄Εστω f : M → N μια αμφιδιαφόριση μεταξύ πολλαπλοτήτων και X,Y λεία διανυσματικά πεδία στη M. Αποδείξτε ότι
![df[X, Y] = [df(X ),df(Y)].](02_chapter_04109x.png)
[1] D. Barden and C. Thomas, An Introduction to Differential Manifolds, Imperial College Press, London, 2003.
[2] W. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry, 2nd ed., Academic Press, Boston, 1986.
[3] W. E. Boyce and R.C. DiPrima, Elementary Differential Equations, 10th ed., WileyPLUS, 2012.
[4] V. Guillemin and A. Pollack, Differential Topology, Prentice-Hall, NJ, 1974.
[5] A. Hatcher, Algebraic Topology, Cambridge University Press, Cambridge, UK, 2002.
[6] J.M. Lee, Introduction to Smooth Manifolds, Springer, New York, 2003.
[7] B. O’ Neill, Semi-Riemannian Geometry with Applications to Relativity, Academic Press 1983.
[8] L. Tu, An Introduction to Manifolds, 2nd ed., Springer, New York, 2011.