Σύνοψη
Παρουσιάζουμε τον ορισμό μιας λείας (διαφορικής) πολλαπλότητας και αναλύουμε δύο βασικά παραδείγματα, την
μοναδιαία σφαίρα και τον προβολικό χώρο. Στη συνέχεια, μελετάμε την έννοια της διαφορισιμότητας μιας
συνάρτησης μεταξύ δύο πολλαπλοτήτων και το θεώρημα αντίστροφης συνάρτησης για πολλαπλότητες. Οι βασικές
αναφορές είναι τα βιβλία [1], [7] και [15].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Βασική Γραμμική Άλγεβρα, Γενική Τοπολογία.
Μια λεία πολλαπλότητα είναι ένα γεωμετρικό αντικείμενο με την ιδιότητα σε κάθε σημείο του να υπάρχει μια περιοχή (που θα ονομάζεται χάρτης) ομοιομορφική με ένα ανοικτό υποσύνολο του ℝn. Οι πολλαπλότητες αποτελούν γενίκευση των καμπυλών και επιφανειών σε μεγαλύτερες διαστάσεις.
Χρειάστηκαν αρκετά χρόνια μέχρι η έννοια της πολλαπλότητας να πάρει τη σημερινή της μορφή. Οι πρώτοι σπόροι της ιδέας βρίσκονται στην εργασία του C. F. Gauss: Disquisitiones generales circa superficies curvas (General Investigations of Curves Surfaces), Commentat. Soc. Göttingensis VI (1827). Στη συνέχεια, ο B. Riemann στην περίφημη ομιλία του στο Göttengen με τίτλο Über die Hypothesen, welche der Geometrie zu Grunde liegen (On the hypotheses that underlie geometry), Habilitation-schrift 1854; Gött. Abh. Ges. Wiss. 13 (1867) (μεταφρ. Θ. Χριστακόπουλος Επί των Σχετικών με τη Γεωμετρία ϒποθέσεων, Εκδ. Τροχαλία 1999), έθεσε το θέμα της διαφορικής γεωμετρίας για οποιαδήποτε διάσταση. Ο Riemann χρησιμοποίησε τη λέξη Mannigfaltigkeit (manifold), για να περιγράψει τα αντικείμενα μελέτης του, όρο που διατήρησε ο H. Poincaré κατά την ανάπτυξη της θεωρίας ομολογίας στο τέλος του 19ου αιώνα. Ο σύγχρονος ορισμός της πολλαπλότητας, χρησιμοποιώντας όρους συνολοθεωρητικής τοπολογίας και συναρτήσεις αλλαγής συντεταγμένων, δόθηκε από τους O. Veblen και J.H.C. Whitehead A set of axioms of differential qeometry, Proceedings of the National Academy of Sciences 17(10)(1931) 551–561 (βλ. και των ιδίων The Foundations of Differential Geometry, Cambridge Univ. Press, 1932).
Μερικοί λόγοι για τους οποίους χρειαζόμαστε την έννοια της πολλαπλότητας είναι οι εξής:
ϒπάρχουν διάφορα ήδη πολλαπλοτήτων, όπως τοπολογικές πολλαπλότητες, πολλαπλότητες κλάσης Ck, αναλυτικές πολλαπλότητες, μιγαδικές πολλαπλότητες. Στο βιβλίο αυτό ενδιαφερόμαστε για τις λείες ή διαφορικές πολλαπλότητες, οι οποίες είναι τοπολογικές πολλαπλότητες εφοδιασμένες με έναν μεγιστικό λείο άτλαντα.
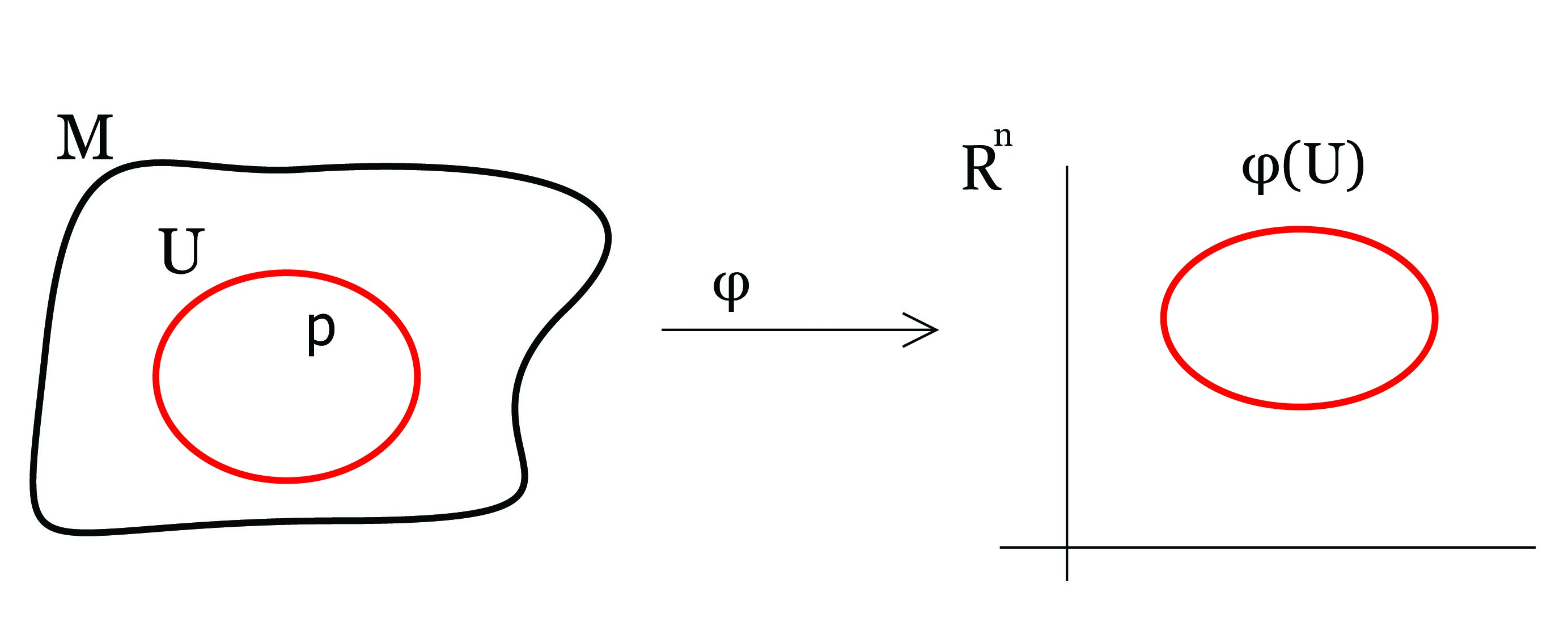
Ορισμός 2.1: ΄Εστω M ένας τοπολογικός χώρος Hausdorff με αριθμήσιμη βάση1. Ο M ονομάζεται τοπολογική πολλαπλότητα (topological manifold) διάστασης n, αν για κάθε σημείο p στον M υπάρχει μια ανοικτή περιοχή U του σημείου p και ένας ομοιομορφισμός φ : U → φ(U) ⊂ ℝn, τέτοιος ώστε το φ(U) να είναι ανοικτό υποσύνολο του ℝn. Τότε λέμε ότι ο τοπολογικός χώρος είναι τοπικά Ευκλείδειος (τοπικά Ευκλείδεια δομή).
Το ζεύγος (U,φ) ονομάζεται τοπικός χάρτης (local chart) ή τοπικό σύστημα συντεταγμένων (local coordinate system) στο p.

Η συνθήκη της τοπικά Ευκλείδειας δομής είναι απαραίτητη προκειμένου να ορίσουμε διαφορισιμότητα συναρτήσεων ορισμένων σε μια πολλαπλότητα. Αυτό θα γίνει χρησιμοποιώντας τη διαφορισιμότητα συναρτήσεων μεταξύ ανοικτών υποσυνόλων του ℝn (όπως την γνωρίζουμε από τον απειροστικό λογισμό).
Αν πi : ℝn → ℝ είναι οι κανονικές προβολές (i = 1,…,n) τότε οι συναρτήσεις xi = πi ∘φ : U ⊂ M → φ(U) → ℝn ονομάζονται τοπικές συντεταγμένες στο p ∈ U.
Προκειμένου η διάσταση μιας τοπολογικής πολλαπλότητας να είναι καλώς ορισμένη, πρέπει να ισχύει ότι αν n≠m, τότε κάθε ανοικτό υποσύνολο του ℝn δεν είναι ομοιομορφικό με ένα ανοικτό υποσύνολο του ℝm. Αυτό είναι ένα δύσκολο αποτέλεσμα, γνωστό ως θεώρημα του αναλλοίωτου της διάστασης. ΄Ενα ανάλογο αποτέλεσμα όμως για λείες πολλαπλότητες είναι πιο εύκολο να αποδειχθεί (και θα το δούμε αργότερα).
Ορισμός 2.2: ΄Εστω M μια τοπολογική πολλαπλότητα και A = 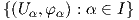 μια συλλογή χαρτών. Η A
ονομάζεται (λείος) άτλαντας, εάν ισχύουν τα παρακάτω:
μια συλλογή χαρτών. Η A
ονομάζεται (λείος) άτλαντας, εάν ισχύουν τα παρακάτω:
Η Ιδιότητα 2 αναφέρεται ως η λεία συμβατότητα των χαρτών (Uα,φα) και (Uβ,φβ). Οι συναρτήσεις φα ∘ φβ-1,φβ ∘ φα-1 ονομάζονται συναρτήσεις αλλαγής συντεταγμένων.
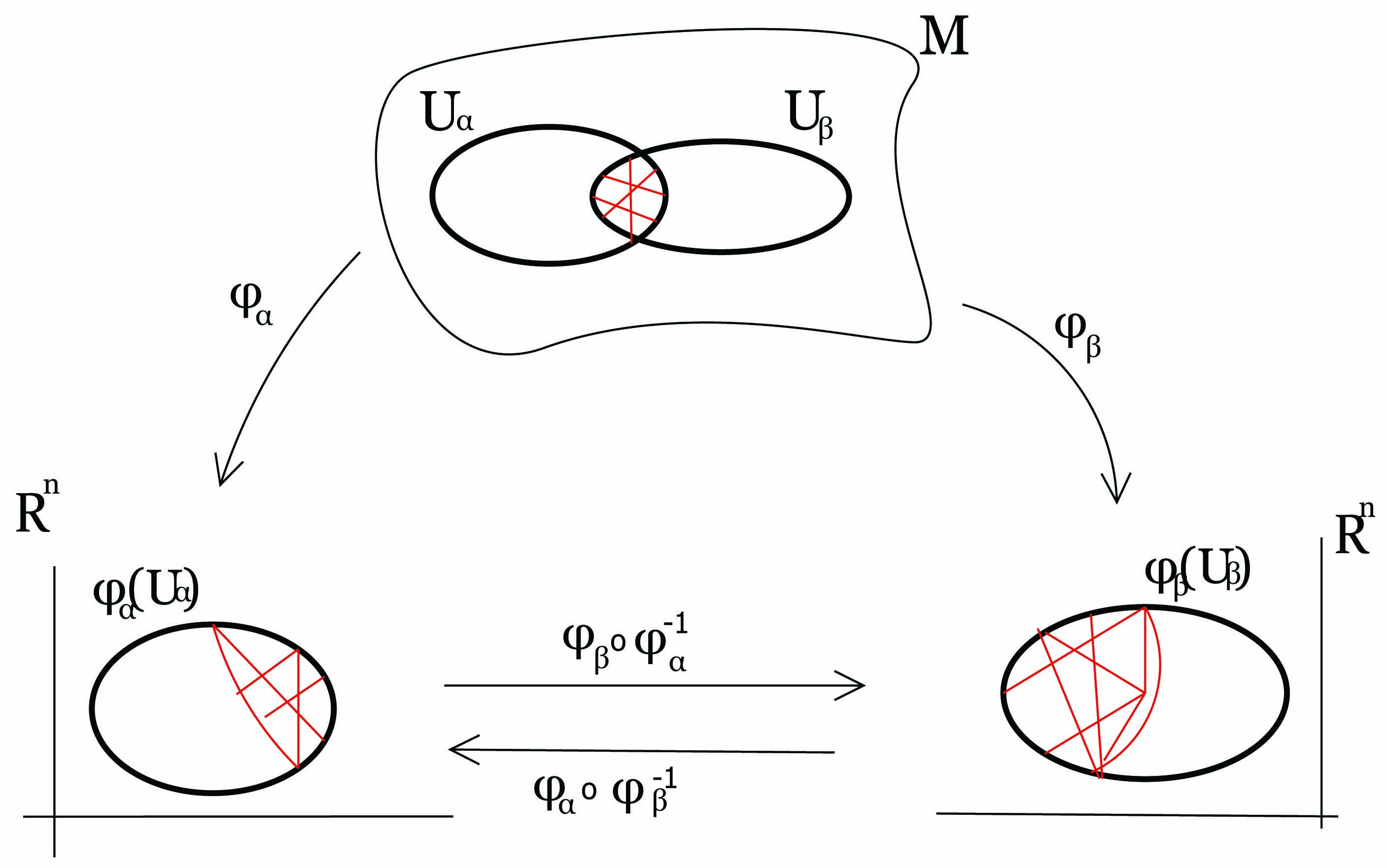
Η σχέση συμβατότητας μεταξύ δύο χαρτών είναι προφανώς ανακλαστική και συμμετρική, αλλά δεν είναι
μεταβατική. Παρ΄ όλα αυτά, αν ορίσουμε ένας χάρτης (U,φ) να είναι συμβατός με έναν άτλαντα 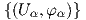 , εάν
είναι συμβατός με όλους τους χάρτες (Uα,φα) του άτλαντα, τότε ισχύει το εξής:
, εάν
είναι συμβατός με όλους τους χάρτες (Uα,φα) του άτλαντα, τότε ισχύει το εξής:
Λήμμα 2.1: ΄Εστω 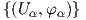 ένας άτλαντας σε έναν τοπικά Ευκλείδειο χώρο. Εάν δύο χάρτες (U,φ) και
(V,ψ) είναι συμβατοί με τον άτλαντα
ένας άτλαντας σε έναν τοπικά Ευκλείδειο χώρο. Εάν δύο χάρτες (U,φ) και
(V,ψ) είναι συμβατοί με τον άτλαντα 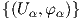 , τότε είναι συμβατοί και μεταξύ τους.
, τότε είναι συμβατοί και μεταξύ τους.
΄Ενας άτλαντας A σε έναν τοπικά Ευκλείδειο χώρο ονομάζεται μεγιστικός άτλαντας (maximal atlas) εάν δεν περιέχεται σε κάποιον μεγαλύτερο άτλαντα. Δηλαδή, αν B είναι ένας άλλος άτλαντας που περιέχει τον A, τότε A = B.
Ορισμός 2.3: Μια λεία ή διαφορική πολλαπλότητα (smooth/differential manifold) είναι μια τοπολογική πολλαπλότητα M εφοδιασμένη με έναν λείο άτλαντα A. Ο μεγιστικός άτλαντας ονομάζεται διαφορική δομή της M. Μια πολλαπλότητα έχει διάσταση n, εάν όλες οι συνεκτικές συνιστώσες της M έχουν διάσταση n.
Μια λεία πολλαπλότητα διάστασης 1 ονομάζεται λεία καμπύλη και μια πολλαπλότητα διάστασης 2 λεία επιφάνεια. ΄Οταν θα γράφουμε πολλαπλότητα θα εννοούμε λεία πολλαπλότητα. Θα αποδείξουμε αργότερα ότι, αν ένα ανοικτό υποσύνολο U του ⊂ ℝn είναι αμφιδιαφορικό με ένα ανοικτό V ⊂ ℝm τότε m = n, συνεπώς η διάσταση μιας λείας πολλαπλότητας είναι καλώς ορισμένη.
Για να αποδείξουμε ότι μια τοπολογική πολλαπλότητα M είναι μια λεία πολλαπλότητα, αρκεί να κατασκευάσουμε κάποιον άτλαντα και όχι απαραίτητα έναν μεγιστικό άτλαντα. Πράγματι, ισχύει το εξής:
Πρόταση 2.1: Κάθε άτλαντας A = 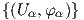 σε έναν τοπικά Ευκλείδειο χώρο περιέχεται σε έναν
μοναδικό μεγιστικό άτλαντα.
σε έναν τοπικά Ευκλείδειο χώρο περιέχεται σε έναν
μοναδικό μεγιστικό άτλαντα.
Παραδείγματα.
1. Ο Ευκλείδειος χώρος ℝn καλύπτεται με έναν μόνο χάρτη U = ℝn,φ = Idℝn, άρα είναι μια πολλαπλότητα
διάστασης n.
2. ΄Εστω M μια πολλαπλότητα διάστασης n με άτλαντα 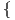 (Uα,φα) : α ∈ I
(Uα,φα) : α ∈ I και έστω V ένα ανοικτό υποσύνολο
της M. Τότε και το V είναι λεία πολλαπλότητα διάστασης n, αφού μπορούμε να ορίσουμε στο V έναν άτλαντα με
περιορισμό των χαρτών (Uα,φα) στο V , δηλαδή
και έστω V ένα ανοικτό υποσύνολο
της M. Τότε και το V είναι λεία πολλαπλότητα διάστασης n, αφού μπορούμε να ορίσουμε στο V έναν άτλαντα με
περιορισμό των χαρτών (Uα,φα) στο V , δηλαδή  (V ∩ Uα,φα|V ∩Uα)
(V ∩ Uα,φα|V ∩Uα) .
.
3. Σε μια πολλαπλότητα διάστασης μηδέν κάθε μονοσύνολο είναι ομοιομορφικό με τον ℝ0, άρα είναι ανοικτό. Συνεπώς, μια τέτοια πολλαπλότητα είναι ένα διακριτό σύνολο και λόγω του δεύτερου αξιώματος αριθμησιμότητας, το διακριτό αυτό σύνολο είναι αριθμήσιμο.
4. Η σφαίρα Sn = {(x1,…,xn+1) ∈ ℝn+1 : ∑ i=1n+1xi2 = 1} είναι μια λεία πολλαπλότητα διάστασης n. Ας δούμε για ευκολία την σφαίρα S2 = {(x1,x2,x3) ∈ ℝ3 : x12 + x22 + x32 = 1}. ΄Εστω N = {(0,0,1)} και S = {(0,0,-1)} ο βόρειος και νότιος πόλος αντίστοιχα. Ορίζουμε δύο χάρτες (U,φ),(V,ψ) της S2 ως εξής: U = S2 \{N},V = S2 \{S} και
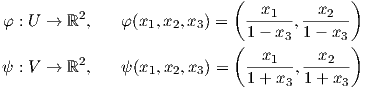
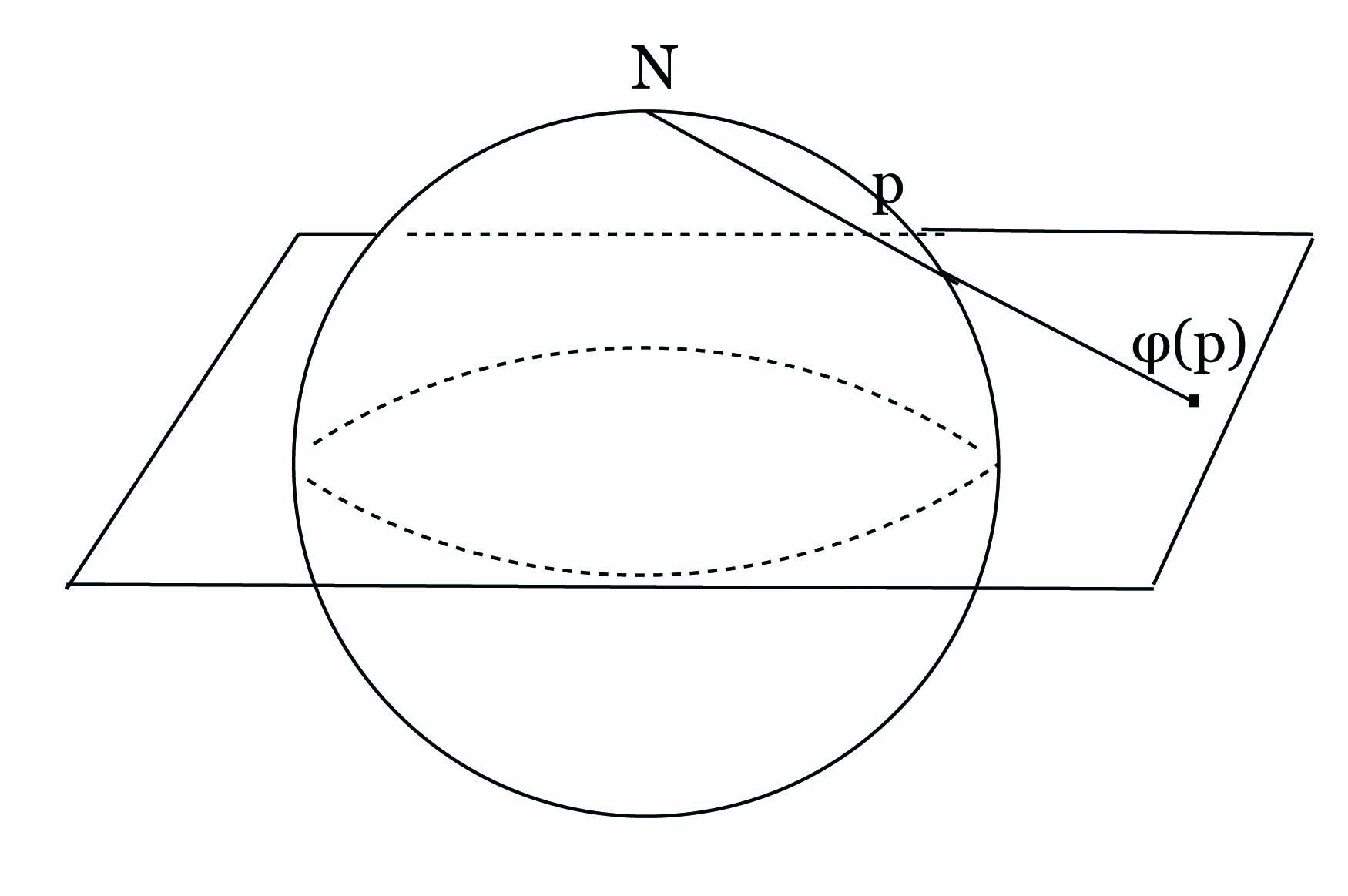
οι στερεογραφικές προβολές. Οι απεικονίσεις φ,ψ είναι 1 - 1 με αντίστροφες τις
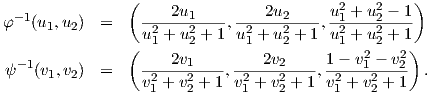
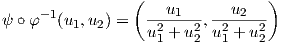
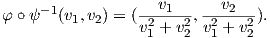
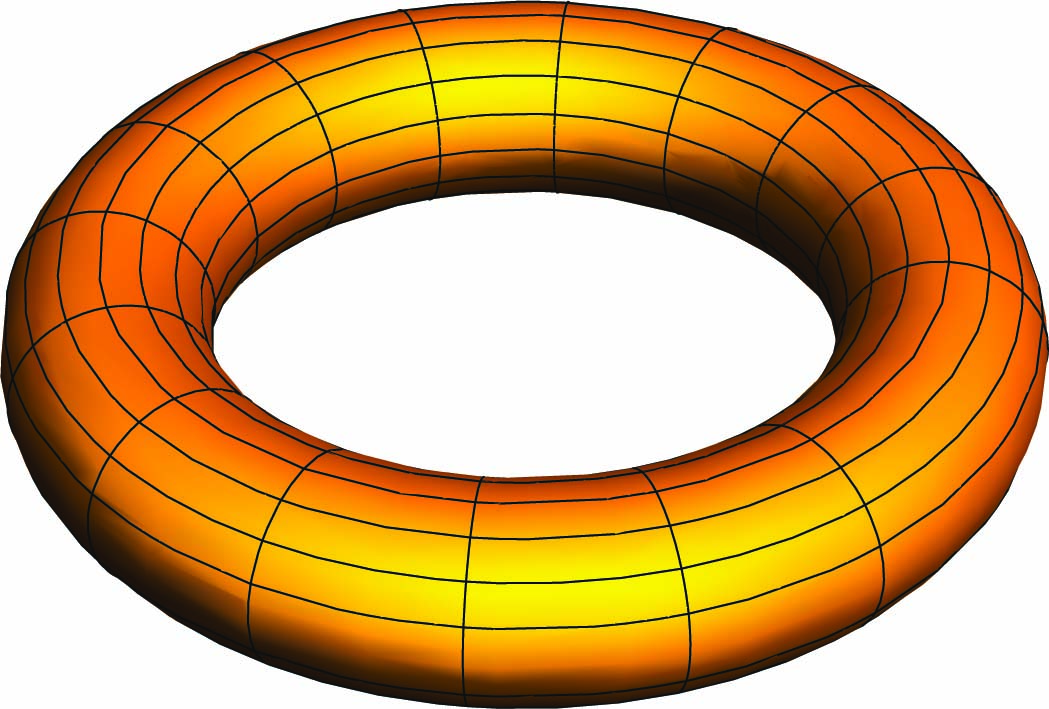
5. Το καρτεσιανό γινόμενο M × N δύο πολλαπλοτήτων M και N είναι λεία πολλαπλότητα. Ως αποτέλεσμα, ο δακτύλιος (torus) S1 × S1 = T2 και ο κύλινδρος S1 × ℝ είναι λείες πολλαπλότητες.
6. Το σύνολο Mm×n(ℝ) όλων των m × n πραγματικών πινάκων είναι ένας διανυσματικός χώρος διάστασης mn. Ως τοπολογικός χώρος είναι ομοιομορφικός με τον ℝmn, άρα σύμφωνα με το Παράδειγμα 1 είναι πολλαπλότητα διάστασης mn.
7. Το σύνολο Glnℝ = {A ∈ Mn×n(ℝ) : det(A)≠0} = det-1(ℝ \{0}) είναι ένα ανοικτό υποσύνολο του Mn×n(ℝ) = Mnℝ, άρα σύμφωνα με το Παράδειγμα 2. είναι πολλαπλότητα διάστασης n2. Το σύνολο Glnℝ είναι επιπλέον μια ομάδα (με πράξη το γινόμενο πινάκων) και ονομάζεται γενική γραμμική ομάδα (general linear group). Παρόμοια ορίζεται η μιγαδική γενική γραμμική ομάδα Glnℂ η οποία είναι μια πολλαπλότητα διάστασης 2n2.
8. Το σύνολο SO(n) = {A ∈ Mnℝ : AAt = In,detA = 1} ονομάζεται ειδική ορθογώνια ομάδα (special linear group). Αποδεικνύεται ότι το σύνολο SO(n) είναι μια λεία πολλαπλότητα διάστασης n(n - 1)∕2. Θα το εξηγήσουμε αυτό αργότερα χωρίς την αναλυτική περιγραφή χαρτών. Προτρέπουμε τον αναγνώστη να αναζητήσει στη βιβλιογραφία την ονομαζόμενη παραμετρικοποίηση του Cayley της ορθογώνιας ομάδας O(n) = {A ∈ Mnℝ : AAt = In}. Μπορούμε να δούμε κάποιες απλές περιπτώσεις:
![{ ( ) }
a b
SO (2) = A = c d : a = d,b = - c,ad - bc = 1
{ ( ) } { ( ) }
a b 2 2 cosθ sin θ
= A = c d : a + b = 1 = - sinθ cos θ : θ ∈ [0,2π] ,](02_chapter_0213x.png)
9. ΄Εστω A ⊂ ℝn και μια συνάρτηση f : A → ℝm. Το γράφημα της f είναι το υποσύνολο του A × ℝm,
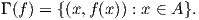

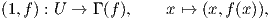
Το επόμενο παράδειγμα είναι ιδιαίτερα σημαντικό, γιαυτό θα το εξετάσουμε χωριστά.
ϒπενθυμίζουμε κάποια θέματα από τη γενική τοπολογία, για τα οποία παραπέμπουμε στα βιβλία [3], [10] και [16].
΄Εστω ~ μια σχέση ισοδυναμίας σε ένα σύνολο M. Η κλάση ισοδυναμίας [x] του x ∈ M αποτελείται από όλα τα
στοιχεία του M που είναι ισοδύναμα με το x. Μια σχέση ισοδυναμίας στο σύνολο M διαμερίζει το M σε κλάσεις
ισοδυναμίας ξένες μεταξύ τους. Το σύνολο όλων των κλάσεων ισοδυναμίας συμβολίζεται με M∕ ~ και ονομάζεται
σύνολο πηλίκο του M μέσω της σχέσης ισοδυναμίας ~. Η απεικόνιση π : M → M∕ ~, x [x], ονομάζεται
κανονική προβολή.
[x], ονομάζεται
κανονική προβολή.
ϒποθέτουμε τώρα ότι το M είναι ένας τοπολογικός χώρος και έστω ~ μια σχέση ισοδυναμίας στον M. Η τοπολογία πηλίκο (quotient topology) στο M∕ ~ ορίζεται ως η τοπολογία για την οποία ένα σύνολο U στο M∕ ~ είναι ανοικτό, εάν και μόνο εάν το π-1(U) είναι ανοικτό στον M. Ο τοπολογικός χώρος M∕ ~ ονομάζεται χώρος πηλίκο (quotient space) και η προβολή π : M → M∕ ~ γίνεται αυτομάτως συνεχής απεικόνιση. Μια σχέση ισοδυναμίας ~ σε έναν τοπολογικό χώρο M ονομάζεται ανοικτή, εάν η προβολή π : M → M∕ ~ είναι ανοικτή απεικόνιση.2 Το γράφημα μιας σχέσης ιδοσυναμίας ~ στον M είναι το υποσύνολο R = {(x,y) ∈ M ×M : x ~ y} του M ×M. Ισχύουν τα εξής:
Πρόταση 2.2: 1. ΄Εστω ~ μια ανοικτή σχέση ισοδυναμίας στον τοπολογικό χώρο M. Τότε ο χώρος πηλίκο M∕ ~ είναι χώρος Hausdorff εάν και μόνο εάν το γράφημα R της ~ είναι ένα κλειστό υποσύνολο του M × M.
2. ΄Ενας τοπολογικός χώρος M είναι χώρος Hausdorff εάν και μόνο εάν η διαγώνιος Δ = {(x,x) ∈ M×M} είναι κλειστό υποσύνολο του M × M.
3. ΄Εστω ~ μια ανοικτή σχέση ισοδυναμίας σε έναν τοπολογικό χώρο M, με αριθμήσιμη βάση. Τότε ο χώρος πηλίκο έχει αριθμήσιμη βάση.
Ερχόμαστε τώρα στον ορισμό του προβολικού χώρου. Ορίζουμε στο σύνολο ℝn+1 \{0} μια σχέση ισοδυναμίας ~ ως εξής: Για x,y ∈ ℝn+1 \{0}
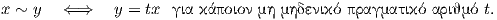
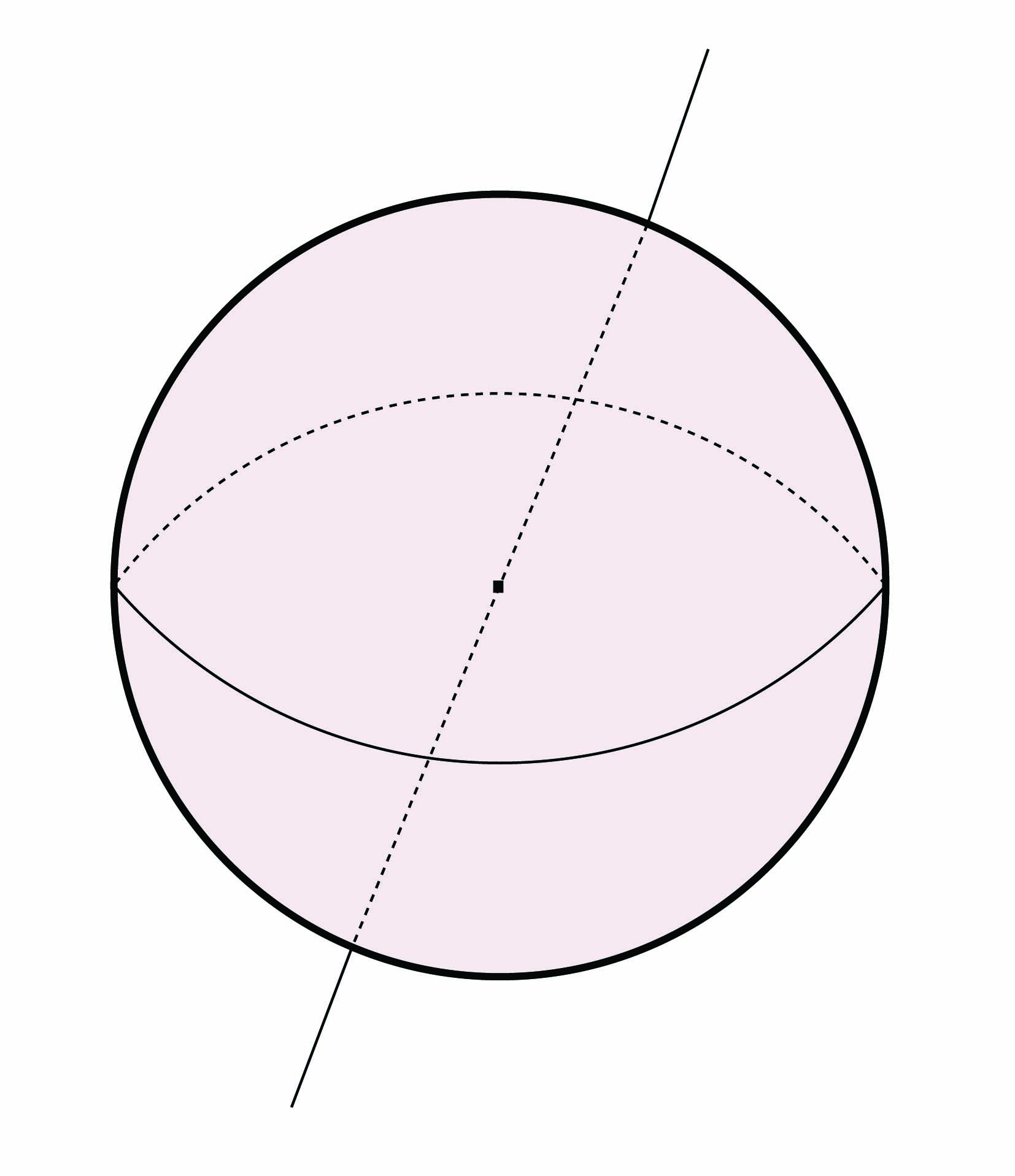
Γεωμετρικά, δύο μη μηδενικά σημεία του ℝn+1 είναι ισοδύναμα εάν και μόνο εάν ανήκουν στην ίδια ευθεία που διέρχεται από την αρχή των αξόνων, συνεπώς ο προβολικός χώρος μπορεί να θεωρηθεί ως το σύνολο όλων των ευθειών που διέρχονται από την αρχή των αξόνων του ℝn+1. Κάθε τέτοια ευθεία τέμνει τη μοναδιαία σφαίρα Sn σε ένα ζεύγος αντιποδικών σημείων. Αντίστροφα, κάθε ζεύγος αντιποδικών σημείων της Sn ορίζει μία και μοναδική ευθεία που διέρχεται από την αρχή των αξόνων του ℝn+1. Ορίζοντας μια σχέση ισοδυναμίας ~ στην Sn ταυτοποιώντας αντιποδικά της σημεία ως
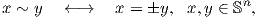
Λόγω της Πρότασης 2.2 ο πραγματικός προβολικός χώρος είναι χώρος Hausdorff και έχει αριθμήσιμη βάση. Θα ορίσουμε τώρα σε αυτόν έναν λείο άτλαντα. ΄Εστω
![0 n n 0
U0 = {[a ,...,a ] ∈ ℝP : a ⁄= 0}.](02_chapter_0220x.png)
![0 n n i
Ui = {[a ,...,a ] ∈ ℝP : a ⁄= 0 }.](02_chapter_0221x.png)
![( a1 an)
φ0 : U0 → ℝn, [a0,...,an] ↦→ -0,..., -0- .
a a](02_chapter_0222x.png)
 [1,b1,…,bn], η οποία είναι και αυτή
συνεχής, άρα είναι ομοιομορφισμός. Παρόμοια, ορίζονται οι ομοιομορφισμοί
[1,b1,…,bn], η οποία είναι και αυτή
συνεχής, άρα είναι ομοιομορφισμός. Παρόμοια, ορίζονται οι ομοιομορφισμοί
![( 0 ^i n)
φi : Ui → ℝn, [a0,...,an] ↦→ a-,...,a-,..., a- ,
ai ai ai](02_chapter_0224x.png)
![( 1 2 n )
[a0,a1,a2...,an]-φ→0 a-, a-,..., a και
a0 a0 a0](02_chapter_0225x.png)
![φ1 (a0 a2 an)
[a0,a1,a2 ...,an]-→ -1-,-1,...,-1- .
a a a](02_chapter_0226x.png)
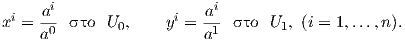
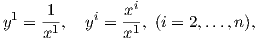
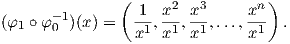
Η έννοια της διαφορισιμότητας μιας απεικόνισης μεταξύ Ευκλειδείων χώρων μπορεί να επεκταθεί σε πολλαπλότητες.
Ορισμός 2.4: ΄Εστω M μια λεία πολλαπλότητα, f : M → ℝ μια συνάρτηση και p ∈ M.
Παρατηρήσεις.
1. Ο παραπάνω ορισμός δεν εξαρτάται από την επιλογή του χάρτη (U,φ). Πράγματι, εάν (V,ψ) είναι ένας άλλος
χάρτης στο p ∈ M, τότε στο σύνολο ψ(U ∩ V ) θα έχουμε ότι
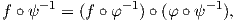
2. Μια λεία συνάρτηση f : M → ℝ στο p είναι και συνεχής στο p. Πράγματι, επειδή η f ∘ φ-1 : φ(U) → ℝ είναι διαφορίσιμη στο φ(p) το οποίο ανήκει σε ένα ανοικτό υποσύνολο του ℝn, θα είναι και συνεχής στο φ(p). Συνεπώς, η f = (f ∘ φ-1) ∘ φ θα είναι συνεχής στο p ως σύνθεση συνεχών απεικονίσεων.
Η παρακάτω πρόταση δείχνει ότι για να αποδείξουμε ότι μία συνάρτηση είναι λεία αρκεί να χρησιμοποιήσουμε τους χάρτες ενός μόνο άτλαντα.
Πρόταση 2.3: ΄Εστω M μια λεία πολλαπλότητα διάστασης n και έστω f : M → ℝ μια λεία συνάρτηση. Τότε τα εξής είναι ισοδύναμα:
Απόδειξη. (ii) ⇒ (i). Προκύπτει από τον ορισμό της λείας συνάρτησης.
(i) ⇒ (iii). ΄Εστω (V,ψ) ένας τυχαίος χάρτης της M και έστω p ∈ V . Τότε λόγω της Παρατήρησης 1. παραπάνω, η συνάρτηση f ∘ ψ-1 είναι λεία στο ψ(p). Επειδή το σημείο p έιναι τυχαίο στο V , η συνάρτηση f ∘ ψ-1 θα είναι διαφορίσιμη στο ψ(V ).
(iii) ⇒ (ii). ΄Αμεσο. ▄
Ερχόμαστε τώρα στον ορισμό μια λείας συνάρτησης μεταξύ δύο πολλαπλοτήτων.
Ορισμός 2.5: ΄Εστω M και N πολλαπλότητες διάστασης m και n αντίστοιχα, f : M → N μια συνεχής απεικόνιση και p ∈ M.

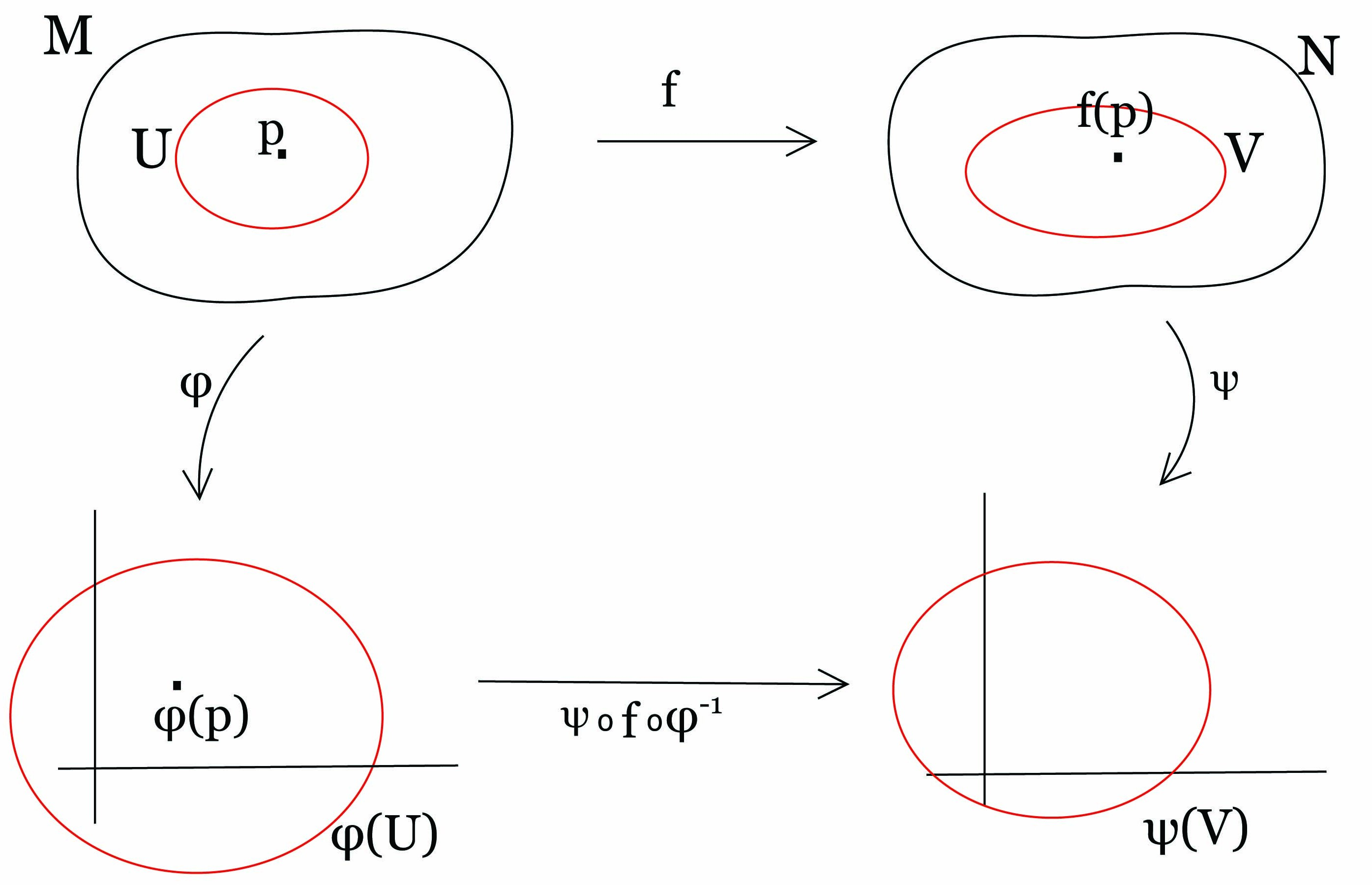
΄Οπως και για την περίπτωση μιας πραγματικής συνάρτησης f : M → ℝ, ο ορισμός δεν εξαρτάται από την επιλογή των χαρτών (άσκηση). Γενικεύοντας την Πρόταση 2.3 προκύπτει ο εξής χαρακτηρισμός λείων συναρτήσεων:
Πρόταση 2.4: ΄Εστω M και N λείες πολλαπλότητες διάστασης m και n αντίστοιχα και έστω f : M → N μια συνεχής απεικόνιση. Τότε τα εξής είναι ισοδύναμα:
Πρόταση 2.5: Αν f : M → N και g : N → P είναι λείες απεικονίσεις μεταξύ πολλαπλοτήτων, τότε η σύνθεση g ∘ f : M → P είναι λεία.
Ορισμός 2.6: Μια λεία απεικόνιση f : M → N μεταξύ πολλαπλοτήτων ονομάζεται αμφιδιαφόριση (diffeomorphism) εάν είναι 1-1, επί και η αντίστροφή της f-1 είναι λεία. Στην περίπτωση αυτή οι πολλαπλότητες M και N ονομάζονται αμφιδιαφορικές.
Αφήνουμε ως ασκήσεις τις παρακάτω προτάσεις.
Πρόταση 2.6: ΄Εστω M μια πολλαπλότητα διάστασης n και (U,φ) ένας χάρτης της. Τότε η συνάρτηση συντεταγμένων φ : U → φ(U) ⊂ ℝn είναι αμφιδιαφόριση.
Πρόταση 2.7: ΄Εστω U ένα ανοικτό υποσύνολο μιας πολλαπλότητας M διάστασης n. Αν f : U → f(U) ⊂ ℝn είναι μια αμφιδιαφόριση και το f(U) είναι ανοικτό υποσύνολο του ℝn, τότε το ζεύγος (U,f) είναι ένας χάρτης που ανήκει στην διαφορική δομή της M.
Παραδείγματα.
1. ΄Εστω f : S2 → ℝ, f(x,y,z) = z η συνάρτηση ύψους (height function). Θα δείξουμε ότι αυτή είναι λεία.
Χρησιμοποιούμε τους χάρτες (U,φ) και (V,ψ) της στερεογραφικής προβολής και πρέπει να δείξουμε ότι οι
απεικονίσεις f ∘ φ-1 και f ∘ ψ-1 είναι λείες. Πράγματι,
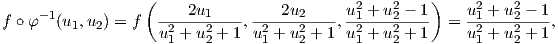
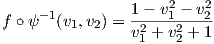
2. ΄Εστω M και N δύο πολλαπλότητες και π : M × N → M, π(p,q) = p η προβολή στον πρώτο παράγοντα του γινομένου. Τότε η π είναι λεία. Πράγματι, έστω (p,q) ∈ M ×N ένα τυχαίο σημείο και έστω (U,φ = (x1,…,xm)), (V,ψ = (y1,…,yn)) συστήματα συντεταγμέων στα p και q αντίστοιχα. Τότε λόγω της ΄Ασκησης 3 το ζεύγος (U × V,φ × ψ) = (U × V ;x1,…,xm,y1,…,yn) είναι ένα σύστημα συντεταγμένων στο σημείο (p,q). Η τοπική αναπαράσταση της π είναι
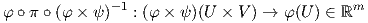
3. Μια ομάδα Lie είναι μια λεία πολλαπλότητα G που είναι επιλέον ομάδα, τέτοια ώστε οι πράξεις μ : G×G → G του πολλαπλασιασμού και i : G → G, i(x) = x-1 της αντιστροφής να είναι λείες. Μερικά παραδείγματα ομάδων Lie είναι ο Ευκλείδειος χώρος ℝn με πράξη την πρόσθεση, το σύνολο ℂ* των μη μηδενικών μιγαδικών αριθμών με πράξη τον πολλαπλασιασμό, ο μοναδιαίος κύκλος S1 ⊂ ℂ , καθώς και η γενική γραμμική ομάδα Glnℝ όλων των n×n πραγματικών αντιστρέψιμων πινάκων. Θα μελετήσουμε τη σημαντική αυτή κατηγορία πολλαπλοτήτων στο Κεφάλαιο 7.
Γενικεύοντας την ΄Ασκηση 1 στην μοναδιαία σφαίρα Sn ⊂ ℝn, μπορούμε να ορίσουμε σε αυτήν μια διαφορική δομή, η οποία ονομάζεται κανονική διαφορική δομή. ΄Ενα από τα πιο αναπάντεχα αποτελέσματα της τοπολογίας ήταν η ανακάλυψη το 1956 από τον John Milnor ([9]) κάποιων λείων πολλαπλοτήτων, οι οποίες είναι ομοιομορφικές, αλλά δεν είναι αμφιδιαφορικές με την σφαίρα S7, εφοδιασμένη με την κανονική διαφορική δομή. Οι σφαίρες αυτές ονομάζονται εξωτικές σφαίρες (exotic spheres). Το 1963 οι Michel Kervaire και John Milnor ([5]) απέδειξαν ότι υπάρχουν ακριβώς 28 διαφορικές δομές στην σφαίρα S7, οι οποίες δεν είναι αμφιδιαφορικές μεταξύ τους. Επίσης, ο Michel Kervaire απέδειξε ότι υπάρχουν τοπολογικές πολλαπλότητες που δεν επιδέχονται καμμία διαφορική δομή ([4]).
Αποδεικνύεται ότι για διαστάσεις μικρότερες του 4 κάθε τοπολογική πολλαπλότητα επιδέχεται μια και μοναδική διαφορική δομή. Για διαστάσεις μεγαλύτερες του 4 κάθε συμπαγής τοπολογική πολλαπλότητα επιδέχεται έναν πεπερασμένο αριθμό διαφορικών δομών. Η διάσταση 4 παραμένει ένα μυστήριο. Για παράδειγμα, δεν είναι γνωστό κατά πόσον η σφαίρα S4 επιδέχεται έναν πεπερασμένο ή άπειρο αριθμό διαφορικών δομών. Η πρόταση αυτή είναι γνωστή ως η λεία εικασία του Poincaré. Παρεμπιπτόντως, η εικασία του Poincaré, η οποία απεδείχθη από τον Grigori Perelman σε τρεις εργασίες το 2002 και 2003 ([11], [12], [13]), αναφέρει ότι κάθε κλειστή, απλά συνεκτική πολλαπλότητα διάστασης 3 είναι ομοιομορφική με την σφαίρα S3.
Θα μεταφέρουμε την έννοια της μερικής παραγαγώγου από έναν Ευκλείδειο χώρο σε ένα τοπικό σύστημα συντεταγμένων μιας πολλαπλότητας, ώστε να γενικεύσουμε το κλασικό θεώρημα αντίστροφης συνάρτησης. Χρησιμοποιώντας το θεώρημα αυτό θα μπορούμε να δώσουμε ένα απλό κριτήριο πότε ένα σύνολο λείων (πραγματικών) απεικονίσεων αποτελούν ένα σύστημα συντεταγμένων στην περιοχή ενός σημείου της πολλαπλότητας. Επιπλέον, σε αρκετές περιπτώσεις, θα μπορούμε να αποδεικνύουμε ευκολότερα ότι ένα σύνολο είναι μια λεία πολλαπλότητα.
΄Εστω f μια λεία (πραγματική) συνάρτηση ορισμένη σε έναν χάρτη (U,φ = (x1,…,xn)) μιας πολλαπλότητας M και έστω p ∈ U. Συμβολίζουμε με u1,…,un τις συντεταγμένες του ℝn. Τότε η συνάρτηση f ∘ φ-1 : (u1,…,un) → f(φ-1(u1,…,un)) ορίζεται στο ανοικτό φ(U) που περιέχει το φ(p), άρα ορίζονται οι συνήθεις περικές παράγωγοι
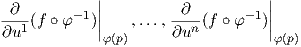
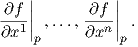
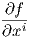 ∘ φ-1 είναι λείες στο φ(U).
∘ φ-1 είναι λείες στο φ(U).
Οι μερικές παράγωγοι σε μια πολλαπλότητα ικανοποιούν την εξής ιδιότητα, αντίστοιχη των μερικών παραγώγων των συναρτήσεων συντεταγμένων του ℝn.
Ορισμός 2.7: ΄Εστω f : M → N μια λεία απεικόνιση και έστω (U,φ) = (U;x1,…,xm), (V,ψ) =
(V,y1,…,yn) δύο χάρτες στις πολλαπλότητες M και N αντίστοιχα, τέτοιοι ώστε f(U) ⊂ V . Συμβολίζουμε
με fi την απεικόνιση yi ∘ f = ui ∘ ψ ∘ f : U → ℝ, δηλαδή την i-συντεταγμένη της f στον χάρτη
(V,ψ). Ο πίνακας 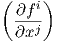 ονομάζεται Ιακωβιανός πίνακας της f ως προς τους χάρτες (U,φ) και (V,ψ).
Εάν οι πολλαπλότητες έχουν την ίδια διάσταση, τότε η ορίζουσα του Ιακωβιανού πίνακα ονομάζεται
Ιακωβιανή ορίζουσα ως προς τους δύο χάρτες. Μερικές φορές η Ιακωβιανή ορίζουσα συμβολίζεται και ως
ονομάζεται Ιακωβιανός πίνακας της f ως προς τους χάρτες (U,φ) και (V,ψ).
Εάν οι πολλαπλότητες έχουν την ίδια διάσταση, τότε η ορίζουσα του Ιακωβιανού πίνακα ονομάζεται
Ιακωβιανή ορίζουσα ως προς τους δύο χάρτες. Μερικές φορές η Ιακωβιανή ορίζουσα συμβολίζεται και ως
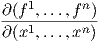 .
.
Μια λεία απεικόνιση f : M → N ονομάζεται τοπικά αντιστρέψιμη ή τοπική αμφιδιαφόριση σε ένα σημείο p ∈ M,
εάν υπάρχει μια περιοχή του p, στην οποία η απεικόνιση 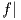 U : U → f(U) να είναι αμφιδιαφόριση. Το κλασικό
θεώρημα αντίστροφης συνάρτησης αναφέρει το εξής ([8], [14]):
U : U → f(U) να είναι αμφιδιαφόριση. Το κλασικό
θεώρημα αντίστροφης συνάρτησης αναφέρει το εξής ([8], [14]):
Θεώρημα 2.1: (Θεώρημα αντίστροφης συνάρτησης στον ℝn). ΄Εστω f : A → ℝn μια λεία απεικόνιση
ορισμένη σε ένα ανοικτό υποσύνολο A του ℝn και έστω p ∈ A. Τότε η f είναι τοπικά αντιστρέψιμη στο p
εάν και μόνο εάν η Ιακωβιανή ορίζουσα det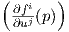 είναι μη μηδενική.
είναι μη μηδενική.
Λόγω του τοπικού χαρακτήρα το θεώρημα γενικεύεται εύκολα σε πολλαπλότητες.
Θεώρημα 2.2: (Θεώρημα αντίστροφης συνάρτησης για πολλαπλότητες). ΄Εστω f : M → N μια λεία
απεικόνιση μεταξύ πολλαπλοτήτων ίδιας διάστασης και έστω p ∈ M. ϒποθέτουμε ότι υπάρχουν χάρτες
(U,φ) = (U;x1,…,xn) στο p και (V,ψ) = (U;y1,…,yn) στο f(p) ∈ N έτσι ώστε f(U) ⊂ V . ΄Εστω
fi = yi∘f. Τότε η f είναι τοπικά αντιστρέψιμη στο p εάν και μόνο εάν η Ιακωβιανή ορίζουσα det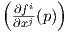 είναι μη μηδενική.
είναι μη μηδενική.
Απόδειξη. Ο Ιακωβιανός πίνακας της f ως προς τους χάρτες (U,φ) και (V,ψ) είναι
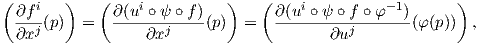
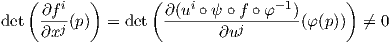
Η βασική εφαρμογή του παραπάνω θεωρήματος στην περίπτωση των πολλαπλοτήτων είναι στο να αποφασίσουμε κατά πόσον ένα σύνολο που περιέχει n λείες συναρτήσεις f1,…,fn σε μια περιοχή ενός σημείου p μιας πολλαπλότητας M διάστασης n, αποτελούν ένα τοπικό σύστημα συντεταγμένων στο p, ενδεχομένως σε μια μικρότερη περιοχή.
Πόρισμα 2.1: ΄Εστω M μια πολλαπλότητα διάστασης n. ΄Ενα σύνολο από n λείες συναρτήσεις f1,…,fn
ορισμένες σε μια περιοχή συντεταγμένων (U;x1,…,xn) ενός σημείου p ∈ M αποτελεί ένα σύστημα
συντεταγμένων στο p εάν και μόνο εάν η Ιακωβιανή ορίζουσα det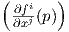 είναι μη μηδενική.
είναι μη μηδενική.
Απόδειξη. Θεωρούμε τη συνάρτηση f = (f1,…,fn) : U → ℝn. Από το θεώρημα αντίστροφης απεικόνισης
για πολλαπλότητες, η Ιακωβιανή ορίζουσα det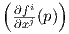 είναι μη μηδενική εάν και μόνο εάν η f : U → ℝn
είναι τοπικά αντιστρέψιμη στο p. Αυτό ισοδυναμεί με το ότι υπάρχει μια περιοχή W του p στην M
ώστε η f : W → f(W) να είναι μια αμφιδιαφόριση (από τον ορισμό της τοπικής αντιστρεψιμότητας).
Χρησιμοποιώντας την Πρόταση 2.7 η τελευταία διατύπωση ισοδυναμεί με το ότι το σύνολο (W;f1,…,fn)
αποτελεί έναν τοπικό χάρτη στο p, ο οποίος ανήκει στην διαφορική δομή της M. ▄
είναι μη μηδενική εάν και μόνο εάν η f : U → ℝn
είναι τοπικά αντιστρέψιμη στο p. Αυτό ισοδυναμεί με το ότι υπάρχει μια περιοχή W του p στην M
ώστε η f : W → f(W) να είναι μια αμφιδιαφόριση (από τον ορισμό της τοπικής αντιστρεψιμότητας).
Χρησιμοποιώντας την Πρόταση 2.7 η τελευταία διατύπωση ισοδυναμεί με το ότι το σύνολο (W;f1,…,fn)
αποτελεί έναν τοπικό χάρτη στο p, ο οποίος ανήκει στην διαφορική δομή της M. ▄
Παράδειγμα 2.1: Θεωρούμε τη συνάρτηση f : ℝ2 → ℝ2, f(x,y) = (x2 +y2 -1,x). Λόγω του θεωρήματος αντίστροφης απεικόνισης, η f είναι μια τοπική αμφιδιαφόριση στο p = (x,y) εάν και μόνο εάν
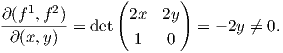
Συνεπώς, οι συναρτησεις f1 = x2 + y2 - 1 και f2 = x είναι δυνατόν να αποτελέσουν ένα σύστημα συντεταγμένων για οποιοδήποτε σημείο p ∈ ℝ2, εκτός των σημείων που βρίσκονται στον άξονα x.
1. Θεωρούμε την σφαίρα S2 = {(x,y,z) ∈ ℝ3 : x2 + y2 + z2 = 1} και ορίζουμε έξι χάρτες σε αυτήν που αντιστοιχούν στα έξι ημισφαίρια (μπρος, πίσω, άνω, κάτω, δεξιά αριστερά) ως εξής:
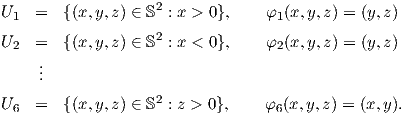
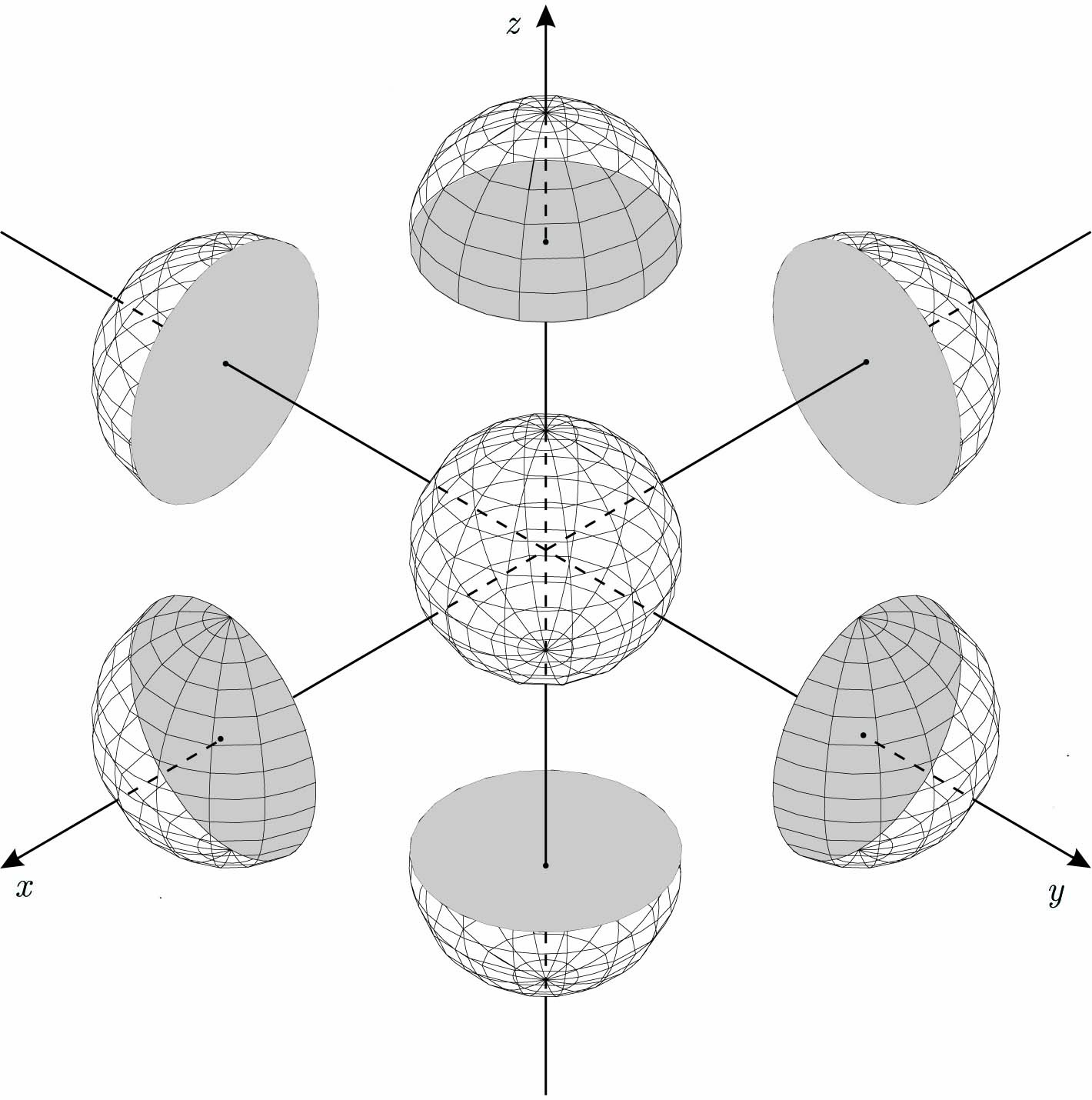
Αποδείξτε ότι ο άτλαντας {(U1,φ1),…,(U6,φ6)} εφοδιάζει την σφαίρα S2 με δομή λείας πολλαπλότητας διάστασης 2. Προσαρμόστε το παράδειγμα αυτό για την περίπτωση του κύκλου S1 = {(x,y) ∈ ℝ2 : x2 + y2 = 1}.
2. Χρησιμοποιήστε το Λήμμα 2.1 και αποδείξτε την Πρόταση 2.1.
3. ΄Εστω M και N λείες πολλαπλότητες. Είναι γνωστό από τη γενική τοπολογία ότι το καρτεσιανό γινόμενο M ×N εφοδιασμένο με την τοπολογία γινόμενο είναι χώρος Hausdorff και έχει αριθμήσιμη βάση. Κατασκευάστε έναν άτλαντα στον M ×N ως εξής: Για δύο απεικονίσεις f : X → X′ και g : Y → Y ′ ορίζουμε το γινόμενό τους ως

4. Αποδείξτε τις Προτάσεις 2.6 και 2.7.
5. Θεωρούμε τους παρακάτω δύο χάρτες του μοναδιαίου κύκλου S1 = {eit : t ∈ [0,2π]}⊂ ℂ:
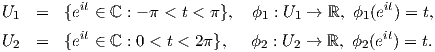
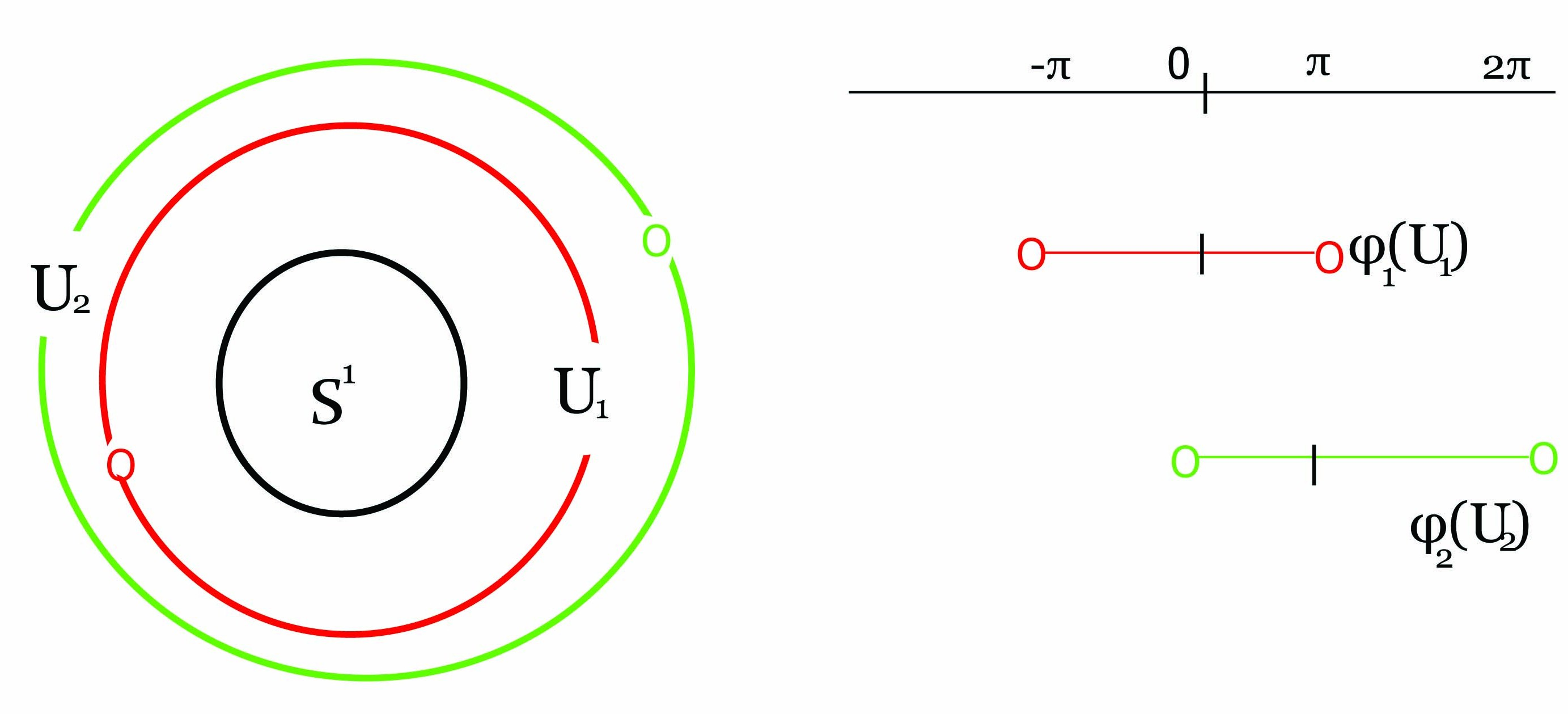
Αποδείξτε ότι οι χάρτες (U1,ϕ1) και (U2,ϕ2) είναι συμβατοί.
ϒπόδειξη: Βρείτε την τομή U1 ∩ U2 (αποτελείται από δύο συνεκτικές συνιστώσες), τις εικόνες ϕ1(U1 ∩ U2), ϕ2(U1 ∩ U2) (αποτελούνται από ένωση δύο διαστημάτων), καθώς και τις συναρτήσεις ϕ2 ∘ ϕ1-1,ϕ1 ∘ ϕ2-1.
6. ΄Εστω x = (x1,…,xn) ∈ ℝn και ||x|| = 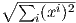 . Αποδείξτε ότι η απεικόνιση
. Αποδείξτε ότι η απεικόνιση
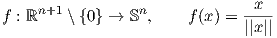
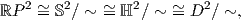
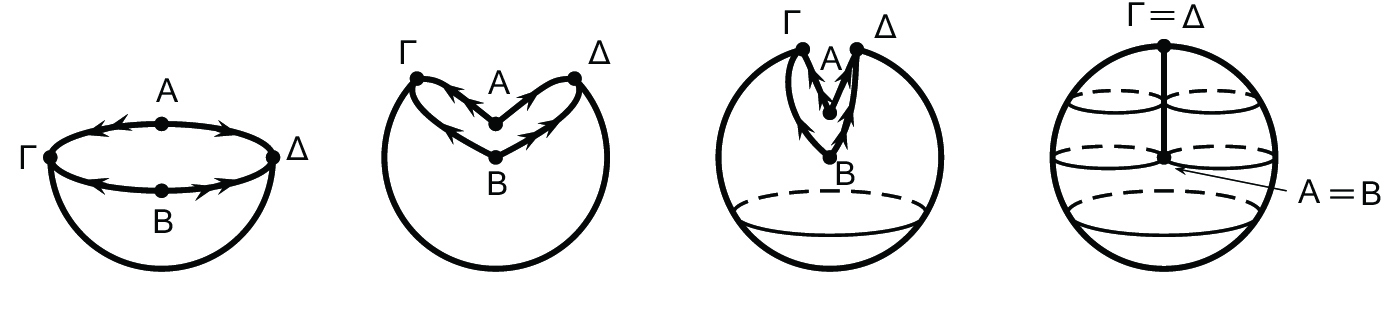
όπου ℍ = {(x,y,z) ∈ ℝ3 : x2 + y2 + z2 = 1,z ≥ 0} και D2 = {(x,y) ∈ ℝ2 : x2 + y2 ≤ 1}.
Στο σύνολο ℍ η σχέση ισοδυναμίας ~ ορίζεται ταυτίζοντας τα αντιποδικά σημεία στον ισημερινό και στο D2 η
σχέση ισοδυναμίας ~ ορίζεται ταυτίζοντας αντιποδικά σημεία στο σύνορο του κύκλου.
Ο πραγματικός προβολικός χώρος ℝPn δεν εμφυτεύεται ως υποπολλαπλότητα του ℝ3, εκτός εάν επιτρέψουμε να έχει αυτοτομές (self-intersections), οπότε τότε απλώς εμβαπτίζεται στον ℝ3 και η επιφάνεια που προκύπτει ονομάζεται επιφάνεια του Werner Boy ([2], [6]), (πρόβλημα που του είχε τεθεί από τον David Hilbert).
7. Είναι δυνατόν να καλυφθεί η σφαίρα S2 με έναν μόνο χάρτη;
8. Αποδείξτε ότι ο πραγματικός προβολικός χώρος ℝPn είναι συμπαγής τοπολογικός χώρος.
9. ΄Εστω f : M → N μια λεία συνάρτηση και έστω p ∈ M. Αν (U,φ) είναι ένας χάρτης στο p και (V,ψ) είναι ένας χάρτης στο f(p) ∈ N, αποδείξτε ότι η τοπική αναπαράσταση ψ ∘ f ∘ φ-1 της f είναι διαφορίσιμη στο σημείο φ(p).
10. Θεωρούμε την πραγματική ευθεία ℝ με δύο μεγιστικούς άτλαντες, τον (ℝ,φ = Id : ℝ → ℝ) και τον (ℝ,ψ : ℝ → ℝ), όπου ψ(x) = x1∕3. Δείξτε ότι οι δύο διαφορικές δομές είναι διαφορετικές μεταξύ τους, δηλαδή ότι η ταυτοτική απεικόνιση Id : (ℝ,φ) → (ℝ,ψ) δεν είναι αμφιδιαφόριση. Παρόλα αυτά, αποδείξτε ότι οι πολλαπλότητες (ℝ,φ) και (ℝ,ψ) είναι αμφιδιαφορικές.
11. Αποδείξτε ότι η απεικόνιση f : S2 → S2,f(x,y,z) = (-x,y,z) είναι λεία.
12. Αποδείξτε ότι οι πολλαπλότητες S1 και ℝP1 είναι αμφιδιαφορικές.
[1] D. Barden and C. Thomas, An Introduction to Differential Manifolds, Imperial College Press, London, 2003.
[2] D. Hilbert and S. Cohn-Vossen, Geometry and the Imagination, AMS Chelsea Publishing, 1952/1999.
[3] K. Jänice, Topology, Springer, New York, 1984.
[4] M. Kervaire, A manifold which does not admit any differentiable structure, Comment. Math. Helv. 34 (1960) 257–270.
[5] M. Kervaire and J. Milnor, Groups of homotopy spheres: I, Ann. of Math. 77 (1963) 504–537.
[6] R. Kirby, What is Boy’s surface?, Notices of the Amer. Math. Soc. 54 (10) (2007) 1306–1307.
[7] J.M. Lee, Introduction to Smooth Manifolds, Springer, New York, 2003.
[8] J.E. Marsden and M.J. Hoffman, Elementary Classical Analysis, 2nd ed., W.H. Freeman, New York, 1993.
[9] J. Milnor, On manifolds homeomorphic to the 7-sphere, Ann. of Math. 64 (1956) 399–405.
[10] J. Munkres, Topology, 2nd ed., Prentice Hall, New Jersey, 2000.
[11] G. Perelman, The entropy formula for the Ricci flow and its geometric applications, Available: arXiv:math/211159 2002.
[12] G. Perelman, Ricci flow with surgery on three-manifolds, Available: arXiv:math/303109 2003.
[13] G. Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds, Available: arXiv:math/307245 2003.
[14] M. Spivak, Calculus on Manifolds, W. A. Benjamin, Inc., New York-Amsterdam 1965. Μετάφραση: Λογισμός σε Πολλαπλότητες, Πανεπιστημιακές Εκδόσεις Κρήτης, 1994.
[15] L. Tu, An Introduction to Manifolds, 2nd ed., Springer, New York, 2011.