Σύνοψη
Στο κεφάλαιο αυτό θα ασχοληθούμε με μια βαθύτερη κατανόηση της καμπυλότητας Gauss. Θα ορίσουμε τα
σύμβολα του Christoffel, τα οποία είναι πραγματικές συναρτήσεις Γijk : U → ℝ σε μια περιοχή παραμέτρησης
X : U → M μιας επιφάνειας M. Οι συναρτήσεις αυτές θα οριστούν ως οι συντελεστές γραμμικών
εκφράσεων των μερικών παραγώγων Xuu,Xuυ, Xυυ ως προς τη βάση {Xu,Xυ,N} του ℝ3. Θα
καταλήξουμε σε δύο σημαντικές ομάδες εξισώσεων, τις εξισώσεις Codazzi και τις εξισώσεις Gauss, οι οποίες
συνδέουν τα θεμελιώδη ποσά πρώτης τάξης E,F,G με την καμπυλότητα K και τα σύμβολα Christoffel
Γijk. Θα φανεί επίσης ότι τα σύμβολα Christoffel εξαρτώνται μόνο από τα E,F,G, άρα θα έχουμε
μια εναλλακτική απόδειξη του Θαυμαστού Θεωρήματος του Gauss. Στη συνέχεια θα δούμε κάποια
σημαντικά αποτελέσματα ολικού χαρακτήρα για μια επιφάνεια (όπως για παράδειγμα το Θεώρημα
του Liebmann). Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7],
[8].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα.
΄Εστω M μια κανονική επιφάνεια του ℝ3 με απεικόνιση Gauss N : M → S2 και έστω X : U ⊂ ℝ2 → M μια τοπική παραμέτρηση της M. Σε κάθε σημείο του X(U) ⊂ M ορίζουμε τη βάση του ℝ3 που αποτελείται από τα διανύσματα {Xu,Xυ,N} και θα μελετήσουμε τις εκφράσεις των παραγώγων των διανυσμάτων Xu,Xυ και των Nu,Nυ ως προς τη βάση αυτή (η μελέτη αυτή είναι ουσιαστικά το ανάλογο των τύπων Frenet στη θεωρία καμπυλών).
Θυμίζουμε ότι σε οποιοδήποτε σημείο X(u,υ) = p, (u,υ) ∈ U είναι
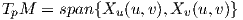
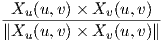 είναι κάθετο στον TpM. Επίσης, θυμίζουμε ότι για τα θεμελιώδη
ποσά δεύτερης τάξης, ισχύουν οι σχέσεις
είναι κάθετο στον TpM. Επίσης, θυμίζουμε ότι για τα θεμελιώδη
ποσά δεύτερης τάξης, ισχύουν οι σχέσεις
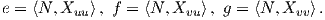 | (7.1) |
Προκειμένου να χρησιμοποιήσουμε τον ιστορικά καθιερωμένο συμβολισμό, θέτουμε u ↔ 1 και υ ↔ 2. Επειδή το σύνολο {Xu,Xυ,N} αποτελεί βάση του ℝ3, υπάρχουν συναρτήσεις Γ111,Γ112,Γ121,Γ122,Γ221 και Γ222 τέτοιες ώστε
όπου λάβαμε υπόψη τις σχέσεις (7.1). Οι πραγματικές συναρτήσεις Γijk (i,j,k ∈{1,2}) επί του U ⊂ ℝ2 ονομάζονται σύμβολα του Christoffel (δεύτερου είδους). Λόγω της σχέσης Xuυ = Xυu προκύπτει ότι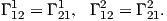
Παράδειγμα 7.1: Θεωρούμε την σφαίρα S2 με τοπική παραμέτρηση
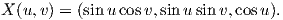
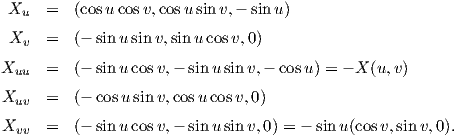
 ) είναι τα εξής:
) είναι τα εξής:
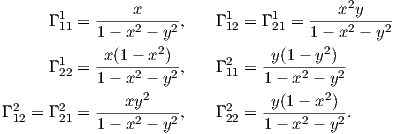
Στη συνέχεια, παίρνουμε τα εσωτερικά γινόμενα στις εξισώσεις (7.2) με τα Xu και Xυ και λαμβάνουμε ότι
Παρατηρούμε τώρα ότι ισχύουν οι εξής σχέσεις:Παρατηρήσεις.
1. Τα πρώτα μέλη των σχέσεων (7.4) ονομάζονται σύμβολα του Christoffel πρώτου είδους και συμβολίζονται με
Γijk, i,j,k = 1,2. Εύκολα βλέπουμε ότι Γijk = Γjik. Επίσης, από τις σχέσεις (7.4) φαίνεται ότι τα σύμβολα
Christoffel πρώτου είδους εκφράζονται συναρτήσει των παραγώγων των θεμελιωδών ποσών πρώτης
τάξης.
2. Αν θέσουμε u = x1,υ = x2 και E = g11,F = g12,G = g22, τότε υπάρχει ο αντίστροφος του
πίνακα1
g = (gij),i,j = 1,2 και αν συμβολίσουμε με gij,k την παράγωγο του gij ως προς xk, τότε οι εξισώσεις (7.4)
γράφονται
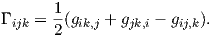
Συνεπώς, λόγω των σχέσεων (7.4) οι σχέσεις (7.3) μπορούν να ξαναγραφτούν ως εξής:
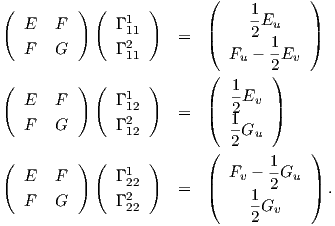
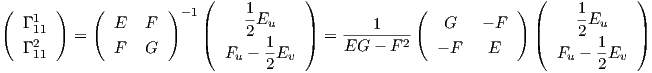 | (7.5) |
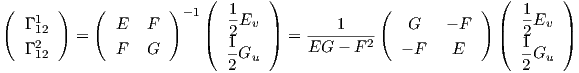 | (7.6) |
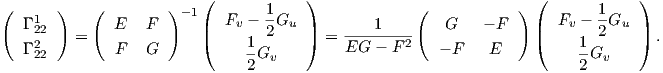 | (7.7) |
Από τις σχέσεις (7.5), (7.6), (7.7) παίρνουμε αντίστοιχα ότι
Παρατήρηση.
Σύμφωνα με την παραπάνω Παρατήρηση 2, αν θέσουμε g-1 = (gkl) τον αντίστροφο του πίνακα g, οι σχέσεις (7.8)
γράφονται ως εξής:
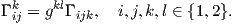
Αυτό το οποίο είναι αξιοσημείωτο από τους παραπάνω τύπους είναι ότι τα σύμβολα του Christoffel, τα οποία καθορίζουν τις εφαπτομενικές συνιστώσες των δεύτερων παραγώγων X.., μπορούν να υπολογιστούν μόνο από τα θεμελιώδη ποσά πρώτης τάξης E,F,G, δηλαδή εξαρτώνται μόνο από την πρώτη θεμελιώδη μορφή της επιφάνειας.
Παράδειγμα 7.2: Θα υπολογίσουμε εκ νέου τα σύμβολα Christoffel για την σφαίρα S2 και θα συγκρίνουμε τα αποτελέσματα με αυτά του Παραδείγματος 7.1. Για την παραμέτρηση που χρησιμοποιήσαμε είναι E = 1,F = 0 και G = sin2u. Χρησιμοποιώντας τις σχέσεις (7.8) παίρνουμε ότι2
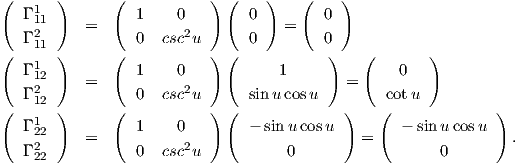
Προκειμένου να προχωρήσουμε, θυμίζουμε ότι αν Sp : TpM → TpM, Sp = -dNp είναι ο τελεστής σχήματος
της επιφάνειας M σε ένα σημείο p ∈ M με πίνακα A = 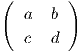 ως προς τη βάση {Xu,Xυ},
τότε
ως προς τη βάση {Xu,Xυ},
τότε
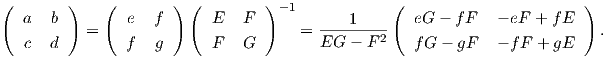 | (7.9) |
Από την προηγούμενη ισότητα προκύπτει ότι οι μερικές παραγώγοι του N ως προς τα u και υ θα είναι
Παραγωγίζουμε τώρα τις εξισώσεις (7.2), χρησιμοποιούμε την ισότητα των μικτών παραγώγων, καθώς και την (7.10) και παίρνουμε: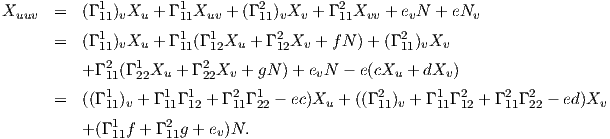
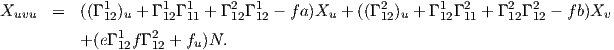
Εξισώσεις Codazzi3
| eυ - fu | = eΓ121 + f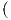 Γ122 - Γ111 Γ122 - Γ111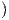 - gΓ112 - gΓ112 |
| fυ - gu | = eΓ221 + f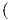 Γ222 - Γ121 Γ222 - Γ121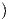 - gΓ122 - gΓ122 |
Χρησιμοποιώντας τώρα τον τύπο για την καμπυλότητα Gauss K = 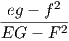 , καθώς και ότι τα στοιχεία του πίνακα
του τελεστή σχήματος δίνονται από τις εξισώσεις
, καθώς και ότι τα στοιχεία του πίνακα
του τελεστή σχήματος δίνονται από τις εξισώσεις
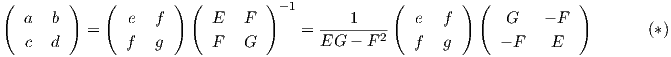
Εξισώσεις Gauss4
| EK | = (Γ112)υ - (Γ122)u + Γ111Γ122 + Γ112Γ222 - Γ121Γ112 - (Γ122)2 |
| FK | = (Γ121)u - (Γ111)υ + Γ122Γ121 - Γ112Γ221 |
| FK | = (Γ122)υ - (Γ222)u + Γ121Γ122 - Γ221Γ112 |
| GK | = (Γ221)u - (Γ121)υ + Γ221Γ111 + Γ222Γ121 - (Γ121)2 - Γ122Γ221. |
΄Ασκηση 1. Αποδείξτε αναλυτικά τις παραπάνω εξισώσεις του Gauss.
Αποδεικνύουμε ενδεικτικά την πρώτη σχέση, χρησιμοποιώντας τη δεύτερη εξίσωση από την σχέση (7.11), ειδικότερα είναι:
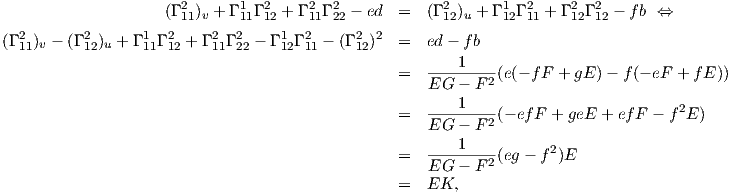
΄Ασκηση 2. Αποδείξτε ότι, αν F = 0, τότε η καμπυλότητα Gauss δίνεται από την σχέση
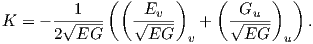
Ως αποτέλεσμα των εξισώσεων Gauss έχουμε μια άλλη απόδειξη του Θαυμαστού Θεωρήματας (Therema Egregium) του Gauss.
Θεώρημα 7.1: (Θαυμαστό Θεώρημα του Gauss) Η καμπυλότητα Gauss καθορίζεται πλήρως από την πρώτη θεμελιώδη μορφή, δηλαδή από τα θεμελιώδη ποσά πρώτης τάξης και τις μερικές παραγώγους αυτών.
Απόδειξη. Από οποιαδήποτε από τις εξισώσεις του Gauss προκύπτει ότι η καμπυλότητα K εκφράζεται μόνο συναρτήσει των E,F,G, των συμβόλων του Christoffel και των παραγώγων τους, συνεπώς εκφράζεται μόνο συναρτήσει των E,F,G και των παραγώγων τους. ▄
Ειδικότερα, η καμπυλότητα Gauss δίνεται από τον τύπο
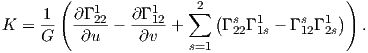
Παρατήρηση.
΄Ενας παρατηρητής ο οποίος βρίσκεται σε μια επιφάνεια χωρίς να έχει την αίσθηση της τρίτης διάστασης και ο
οποίος μπορεί να μετρά τοπικά μήκη και γωνίες, μπορεί να υπολογίσει τα θεμελιώδη ποσά πρώτης τάξης E,F,G,
άρα σύμφωνα με το Θαυμαστό Θεώρημα του Gauss μπορεί να υπολογίσει την καμπυλότητα K = κ1κ2. Παρόλα
αυτά έχει όμως τη δυνατότητα να υπολογίσει χωριστά τις κύριες καμπυλότητες κ1 και κ2, πράγμα που θα
απαιτούσε τη γνώση της μεταβολής του κάθετου διανύσματος N. Αυτό σημαίνει ότι, για παράδειγμα, με γνώση
μόνο της καμπυλότητας Gauss δεν μπορεί να διακρίνει αν βρίσκεται σε έναν κύλινδρο (κ1 = 0,κ2 = -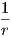 ) ή σε ένα
επίπεδο (κ1 = 0,κ2 = 0), αφού οι δύο αυτές επιφάνειες έχουν την ίδια πρώτη θεμελιώδη μορφή και
K = 0.
) ή σε ένα
επίπεδο (κ1 = 0,κ2 = 0), αφού οι δύο αυτές επιφάνειες έχουν την ίδια πρώτη θεμελιώδη μορφή και
K = 0.
Πόρισμα 7.1: Αν δύο επιφάνειες είναι τοπικά ισομετρικές, τότε οι αντίστοιχες καμπυλότητες Gauss είναι ίσες.
Παράδειγμα 7.3: ΄Εστω X : ℝ × ℝ+ → M μια παραμέτρηση μιας επιφάνεια M με θεμελιώδη ποσά
πρώτης τάξης E(u,υ) = G(u,υ) = υ και F(u,υ) = 0. Τότε η επιφάνεια M δεν είναι δυνατόν να είναι
τοπικά ισομετρική με μια σφαίρα. Πράγματι, από την σχέση (7.8) παίρνουμε ότι Γ111 = 0,Γ112 = -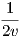 ,
Γ121 =
,
Γ121 = 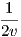 ,Γ122 = 0, Γ
221 = 0,Γ222 =
,Γ122 = 0, Γ
221 = 0,Γ222 = 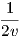 . Από το Θαυμαστό Θεώρημα θα είναι:
. Από το Θαυμαστό Θεώρημα θα είναι:
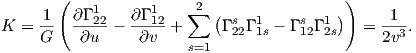
Οι εξισώσεις Codazzi μαζί με οποιαδήποτε από τις εξισώσεις Gauss ονομάζονται εξισώσεις συμβατότητας της θεωρίας επιφανειών.
΄Ενα ερώτημα είναι κατά πόσον υπάρχουν και άλλες εξισώσεις συμβατότητας μεταξύ των θεμελιωδών ποσών πρώτης και δεύτερης τάξης για μια επιφάνεια εκτός από τις παραπάνω. Η απάντηση είναι αρνητική. Με άλλα λόγια, διαδοχικές παραγωγίσεις ή άλλες πράξεις δεν είναι δυνατόν να δώσουν επιπλέον σχέσεις μεταξύ των συναρτήσεων E,F,G,e,f,g και των παραγώγων τους.
Το παρακάτω θεώρημα δίνει ακριβώς την απάντηση.
Θεώρημα 7.2: (Bonnet) ΄Εστω E,F,G,e,f,g : V ⊂ ℝ2 → ℝ διαφορίσιμες συναρτήσεις στο ανοικτό σύνολο V με E > 0 και G > 0. ϒποθέτουμε ότι οι συναρτήσεις αυτές ικανοποιούν τις εξισώσεις Codazzi και Gauss (μία από αυτές) και ότι EG - F2 > 0. Τότε για κάθε q ∈ V υπάρχει ανοικτό U ⊂ V με q ∈ U και αμφιδιαφόριση X : U → X(U) ⊂ ℝ3, τέτοια ώστε η κανονική επιφάνεια X(U) ⊂ ℝ3 να έχει τις συναρτήσεις E,F,G,e,f και g ως τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης. Στην περίπτωση που το U είναι συνεκτικό, η αμφιδιαφόριση X είναι μοναδική, μη λαμβάνοντας υπόψη στερεές κινήσεις του ℝ3.
Ουσιαστικά το θεώρημα αυτό είναι ανάλογο της θεωρίας καμπυλών, διότι μας εξασφαλίζει την ύπαρξη επιφάνειας με δεδομένα τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης.
Η απόδειξη δεν είναι ιδιαίτερα απλή. Χρειαζόμαστε αποτελέσματα θεωρίας διαφορικών εξισώσεων με μερικές παραγώγους (βλ. [1], [3])
Οι εξισώσεις Coodazzi και Gauss είναι ιδαίτερα δύσκολες στη χρήση τους στη γενική τους μορφή, αλλά κάποιες ειδικές περιπτώσεις έχουν ενδιαφέρουσες εφαρμογές και ταυτόχρονα αναδεικνύουν την αξία τους. Παρακάτω θα παρουσιάσουμε κάποιες από αυτές. Θυμίζουμε πρώτα κάποιους ορισμούς.
Ορισμός 7.1: ΄Εστω M ⊂ ℝ3 μια προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2. Μια γραμμή καμπυλότητας (line of curvature) στην M είναι μια καμπύλη γ : I → M, τέτοια ώστε το διάνυσμα γ′(t) να είναι πάντα μια κύρια διεύθυνση.
Ορισμός 7.2: ΄Εστω X : U ⊂ ℝ2 → M μια τοπική παραμέτρηση μιας επιφάνειας M και (u,υ) οι
συντεταγμένες στο U. Μια u-καμπύλη (αντίστοιχα υ-καμπύλη) στην M είναι μια καμπύλη της μορφής
u X(u,υ0) (αντίστοιχα υ
X(u,υ0) (αντίστοιχα υ X(u0,υ)).
X(u0,υ)).
Αν τώρα οι μεταβλητές u,υ παίρνουν όλες τις τιμές στο U, τότε ορίζεται ένα πλέγμα επιφανειακών καμπύλων στην M που την καλύπτουν. Το πλέγμα αυτό ονομάζεται γραμμές συντεταγμένων (coordinate lines) της M. Το ερώτημα είναι πότε οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας. Ισχύει το εξής:
Πρόταση 7.1: ΄Εστω X : U → M ⊂ ℝ3 μια τοπική παραμέτρηση μιας κανονικής επιφάνειας M και έστω ότι το σύνολο X(U) δεν περιέχει ομφαλικά σημεία (δηλαδή με ίσες κύριες καμπυλότητες). Τότε μια γραμμή συντεταγμένων είναι και γραμμή καμπυλότητας εάν και μόνο εάν ισχύει F ≡ f ≡ 0.
Απόδειξη. Το γεγονός ότι οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας ισοδυναμεί με το ότι οι
διευθύνσεις των γραμμών συντεταγμένων είναι πάντα κύριες διευθύνσεις. Αυτό με τη σειρά του ισοδυναμεί
με το ότι ο πίνακας A του τελεστή σχήματος ως προς τη βάση {Xu,Xυ} είναι πάντα διαγώνιος. Λαμβάνοντας
τώρα υπόψη την έκφραση (*), προκύπτει ότι αν F ≡ f ≡ 0, τότε ο πίνακας A είναι διαγώνιος, άρα οι γραμμές
συντεταγμένων είναι γραμμές καμπυλότητας. Αντίστροφα, υποθέτουμε ότι οι γραμμές συντεταγμένων είναι
γραμμές καμπυλότητας. Αυτό σημαίνει ότι τα διανύσματα Xu,Xυ είναι κύριες διευθύνσεις. Επειδή δεν
υπάρχουν ομφαλικά σημεία, τα διανύσματα Xu,Xυ είναι κάθετα, άρα F = 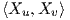 = 0. Συνεπώς, τα
εκτός διαγωνίου στοιχεία του πίνακα A στην έκφραση (*) είναι
= 0. Συνεπώς, τα
εκτός διαγωνίου στοιχεία του πίνακα A στην έκφραση (*) είναι 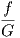 και
και 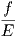 και επειδή αυτά πρέπει να είναι
μηδέν παίρνουμε ότι f ≡ 0. Σημειώστε ότι στα ομφαλικά σημεία όλες οι διευθύνσεις είναι κύριες διεθύνσεις,
άρα σε αυτά οι γραμμές συντεταγμένων είναι πάντα γραμμές καμπυλότητας. ▄
και επειδή αυτά πρέπει να είναι
μηδέν παίρνουμε ότι f ≡ 0. Σημειώστε ότι στα ομφαλικά σημεία όλες οι διευθύνσεις είναι κύριες διεθύνσεις,
άρα σε αυτά οι γραμμές συντεταγμένων είναι πάντα γραμμές καμπυλότητας. ▄
Λήμμα 7.1: ϒποθέτουμε ότι X είναι μια παραμέτρηση, για την οποία οι γραμμές συντεταγμένων (δηλαδή οι u-καμπύλες και οι υ-καμπύλες) είναι γραμμές καμπυλότητας με αντίστοιχες κύριες καμπυλότητες k1 και k2. Τότε ισχύουν οι σχέσεις
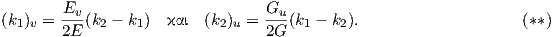
Απόδειξη. Λόγω της Πρότασης 7.1 είναι F ≡ 0 ≡ f. Τότε οι εξισώσεις Codazzi απλουστεύονται ως

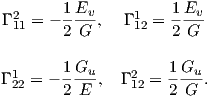
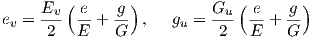 | (7.13) |
Λαμβάνοντας υπόψη τη μορφή του πίνακα του τελεστή σχήματος (*) και ότι F = 0 = f, προκύπτει ότι
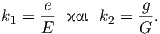
Ερχόμαστε τώρα στην πρώτη ενδιαφέρουσα εφαρμογή των εξισώσεων Codazzi, όπου K ≡ 0.
Πρόταση 7.2: ΄Εστω M μια αναπτυκτή επιφάνεια (δηλαδή K ≡ 0) χωρίς επίπεδα σημεία (δηλαδή σημεία p όπου k1(p) = k2(p) = 0). Τότε η M είναι ένας γενικευμένος κύλινδρος, του οποίου το εφαπτόμενο επίπεδο παραμένει σταθερό κατά μήκος των γεννητόρων.
Απόδειξη. Επειδή η M είναι επίπεδη και δεν περιέχει επίπεδα σημεία, μπορούμε να υποθέσουμε ότι k1 = 0 και
k2≠0 παντού. Συνεπώς, υπάρχει μια τοπική παραμέτρηση X της M, για την οποία οι γραμμές συντεταγμένων
είναι γραμμές καμπυλότητας (οι u-καμπύλες να αντιστοιχούν στην k1 και οι υ-καμπύλες στην k2). (Αυτό
δεν είναι εντελώς προφανές, ανάγεται σε θέμα διαφορικών εξισώσεων βλ. Shifrin σελ. 119–120). Αυτό
σημαίνει ότι μπορούμε να επιλέξουμε την παραμέτρηση X, ώστε F = f = 0. Επειδή k1 = 0, τότε για
κάθε p ∈ M θα είναι Sp(Xu) = 0, άρα Nu = 0 παντού. Συνεπώς, το διάνυσμα N θα είναι σταθερό κατά
μήκος των u-καμπυλών. Επίσης, παρατηρούμε ότι e = 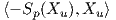 = 0. Θέλουμε τώρα να δείξουμε ότι
οι u-καμπύλες είναι ουσιαστικά ευθείες. Επειδή k1 = 0 παντού, θα είναι και (k1)υ = 0 και δεδομένου ότι
k2≠k1, λόγω του Λήμματος 7.1 προκύπτει ότι Eυ = 0. Τότε η εξίσωση (7.5) δίνει ότι Γ112 = 0, συνεπώς
= 0. Θέλουμε τώρα να δείξουμε ότι
οι u-καμπύλες είναι ουσιαστικά ευθείες. Επειδή k1 = 0 παντού, θα είναι και (k1)υ = 0 και δεδομένου ότι
k2≠k1, λόγω του Λήμματος 7.1 προκύπτει ότι Eυ = 0. Τότε η εξίσωση (7.5) δίνει ότι Γ112 = 0, συνεπώς
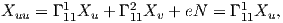
Οι επίπεδοι γενικευμένοι κύλινδροι συχνά ονομάζονται και αναπτυκτές επιφάνειες (developable surfaces). Το όνομα αυτό οφείλεται στο γεγονός ότι αυτές οι επιφάνειες μπορούν να απεικονιστούν ισομετρικά πάνω σε ένα επίπεδο. Δύο άλλες κατηγορίες αναπτυκτών επιφανειών είναι οι επιφάνειες που σχηματίζονται από τις εφαπτόμενες μιας καμπύλης του ℝ3 και οι κωνικές επιφάνειες. Στη συνέχεια, θα αποδείξουμε ένα ολικό αποτέλεσμα για συμπαγείς επιφάνειες.
Θεώρημα 7.3: (Liebmann) ΄Εστω M μια συμπαγής κανονική επιφάνεια με σταθερή καμπυλότητα Gauss K.
Τότε K > 0 και η M θα είναι μια σφαίρα ακτίνας 1∕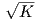 .
.
Χρειαζόμαστε πρώτα το εξής:
Λήμμα 7.2: (Hilbert) ΄Εστω p ένα σημείο μιας επιφάνειας το οποίο δεν είναι ομφαλικό και ότι k1(p) > k2(p). ϒποθέτουμε ότι η k1 έχει τοπικό μέγιστο στο p και η k2 τοπικό ελάχιστο στο p. Τότε K(p) ≤ 0.
Απόδειξη. Επειδή k1(p)≠k2(p), υπάρχει τοπική παραμέτρηση στο p, ώστε οι u-καμπύλες να είναι γραμμές καμπυλότητας με κύρια καμπυλότητα k1 και οι υ-καμπύλες να είναι γραμμές καμπυλότητας με κύρια καμπυλότητα k2. Επειδή k1≠k2 και (k1)υ = (k2)u = 0, στο σημείο p, από το Λήμμα 2.1 προκύπτει ότι Eυ = Gu = 0 στο p. Παραγωγίζοντας τις σχέσεις (**) και λαμβάνοντας υπόψη ότι (k1)u = (k2)υ = 0, προκύπτει ότι στο σημείο p ισχύουν οι σχέσεις
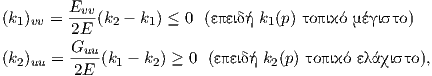
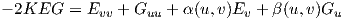
Απόδειξη. (του Θεωρήματος 2.3). Επειδή η M είναι συμπαγής, υπάρχει ένα σημείο με θετική καμπυλότητα Gauss και επειδή από υπόθεση αυτή είναι σταθερή στην M, τότε θα είναι K > 0, άρα αποδείχτηκε το πρώτο μέρος του θεωρήματος. Εάν όλα τα σημεία της M είναι ομφαλικά, τότε η M είναι μια σφαίρα. Εάν υπάρχει τουλάχιστον ένα μη ομφαλικό σημείο, τότε επειδή η M είναι συμπαγής, η μεγαλύτερη κύρια καμπυλότητα k1 λαμβάνει μέγιστη τιμή σε κάποιο p ∈ M. Επειδή η K = k1k2 είναι σταθερή, η συνάρτηση k2 = K∕k1 πρέπει να λαμβάνει ελάχιστη τιμή στο σημείο p. Δεδομένου ότι το σημείο p δεν μπορεί να είναι ομφαλικό, (γιατί;) τότε λόγω του Λήμματος 7.2 θα είναι K(p) ≤ 0, πράγμα άτοπο. ▄
΄Ασκηση 3. Αποδείξτε ότι αν M είναι μια συμπαγής και συνεκτική (προσανατολισμένη) επιφάνεια με K > 0 και H
σταθερή, τότε η M είναι μια σφαίρα ακτίνας 1∕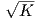 . (ϒπόδειξη. Θεωρήστε τη συνάρτηση H2 -K = (k1 -k2)2∕4
και έστω p ∈ M ένα σημείο μεγίστου. Εξετάστε τις περιπτώσεις H2 - K(p) = 0 και H2 - K(p) > 0 και
χρησιμοποιείστε το Θεώρημα Liebmann και το Λήμμα του Hilbert αντίστοιχα.)
. (ϒπόδειξη. Θεωρήστε τη συνάρτηση H2 -K = (k1 -k2)2∕4
και έστω p ∈ M ένα σημείο μεγίστου. Εξετάστε τις περιπτώσεις H2 - K(p) = 0 και H2 - K(p) > 0 και
χρησιμοποιείστε το Θεώρημα Liebmann και το Λήμμα του Hilbert αντίστοιχα.)
Παράδειγμα 7.4: Αν φ είναι η γωνία των παραμετρικών γραμμών u =σταθερό, υ =σταθερό, της επιφάνειας M, τότε ισχύουν οι σχέσεις
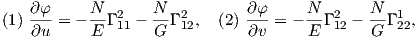
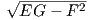 .
.
Λύση
(1) Είναι γνωστό ότι η γωνία των παραμετρικών γραμμών u =σταθερό και υ =σταθερό δίνεται από τη σχέση
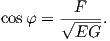 | (7.14) |
Παραγωγίζουμε την σχέση αυτή ως προς u:
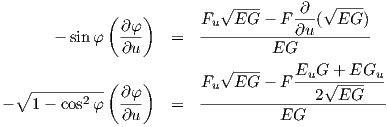
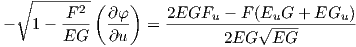
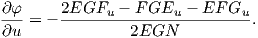 | (7.15) |
Αλλά το δεύτερο μέρος της προς απόδειξη σχέσης γράφεται
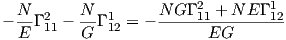
Παράδειγμα 7.5: Αν N = N(u,υ) είναι το μέτρο του κάθετου διανυσματικού πεδίου της επιφάνειας M με τοπική παραμέτρηση X : U ⊂ ℝ2 → M, τότε ισχύουν οι ακόλουθες σχέσεις
Λύση
(1) Γνωρίζουμε ότι
 | (7.17) |
όπου E,F και G είναι τα θεμελιώδη ποσά πρώτης τάξης της επιφάνειας M. Το πρώτο μέρος της προς απόδειξη σχέσης λόγω της (7.17) γράφεται
Παράδειγμα 7.6: Δίνεται η τετραγωνική μορφή A = du2 + cos2udυ2. Να εξετασθεί εαν υπάρχει επιφάνεια του ℝ3 για την οποία ισχύει η σχέση I = II = A. Σε καταφατική περίπτωση να βρεθεί μια τοπική παραμέτρηση αυτής.
Λύση
Εφόσον I = A, θα είναι
 | (7.18) |
Επίσης από την σχέση II = A έπεται ότι
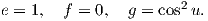 | (7.19) |
Παρατηρούμε λοιπόν ότι
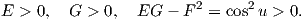 | (7.20) |
Για να υπάρχει επιφάνεια που να έχει ως θεμελιώδη ποσά τις συναρτήσεις που δίνονται από τις (7.18) και (7.19), θα πρέπει επιπλέον να ικανοποιείται η θεμελιώδης εξίσωση του Gauss και οι εξισώσεις Codazzi. Θα δείξουμε πρώτα το Θεώρημα Egregium. Κατ΄ αρχάς είναι
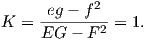 | (7.21) |
΄Ομως
΄Αρα ισχύει το θεώρημα Egregium. Θα εξετάσουμε τώρα την ισχύ των εξισώσεων Codazzi. Αφού όμως F = f = 0, αρκεί να δειχθούν οι εξισώσεις αυτές στη μορφή Αλλά από τις (7.18) και (7.19) είναι προφανές ότι eυ = Eυ = 0 και επομένως η πρώτη εκ των σχέσεων είναι αληθής. Επίσης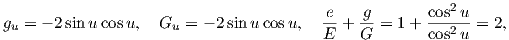
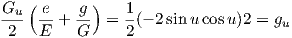
Σχετικά με το δεύτερο μέρος του ερωτήματος, έστω X : U ⊂ ℝ2 → M μια τοπική παραμέτρηση της ζητούμενης επιφάνειας για την οποία ισχύουν
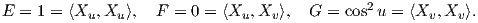
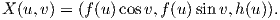 | (7.24) |
Ως εκ τούτου η σχέση E = 1 παίρνει τη μορφή
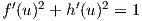 | (7.25) |
και η σχέση G = cos2u τη μορφή f(u)2 = cos2u, άρα είναι
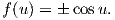 | (7.26) |
Εύκολα όμως από την (7.24) προκύπτει ότι
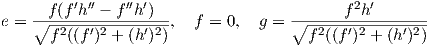 | (7.27) |
και λόγω των σχέσεων (7.19) οι εξισώσεις αυτές ισοδύναμα γράφονται ως εξής
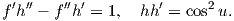 | (7.28) |
Πράγματι, από την (7.25) συνεπάγεται ότι h′(u)2 = cos2u, οπότε
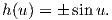 | (7.29) |
Η πρώτη εκ των (7.28), λόγω των (7.26) και (7.29) γίνεται
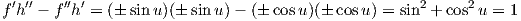 | (7.30) |
και η δεύτερη fh′ = cos2u. Οι ζητούμενες λοιπόν συναρτήσεις f(u) και h(u) ορίζονται από τις σχέσεις (7.26) και (7.29) και επομένως η ζητούμενη τελικά επιφάνεια θα ορίζεται από την ακόλουθη παραμέτρηση
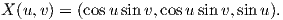
1. Για την επιφάνεια εκ περιστροφής X(u,υ) = (f(υ)cosu,f(υ)sinu,g(υ)), f(υ)≠0 να αποδειχθεί ότι
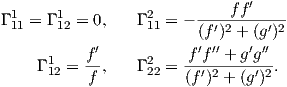
2. Δίνεται η επιφάνεια M με εξίσωση z = z(x,y). ΄Εστω p = zx,q = zy, r = zxx,s = zxy, t = zyy και
N = 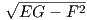 . Να αποδειχθεί ότι ισχύουν οι σχέσεις
. Να αποδειχθεί ότι ισχύουν οι σχέσεις
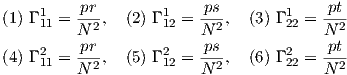
3. Δίνεται η τετραγωνική μορφή A = du2 + sin2udυ2. Να εξετασθεί εάν υπάρχει επιφάνεια του ℝ3, για την οποία I = II = A.
4. Να εξετασθεί εάν υπάρχει επιφάνεια της οποίας τα θεμελιώδη ποσά να είναι
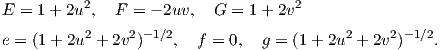
5. Να βρεθεί η επιφάνεια του ℝ3 της οποίας τα θεμελιώδη ποσά είναι E = G = 1,F = 0, e = -1, f = g = 0.
6. Δείξτε ότι δεν υπάρχει τμήμα επιφάνειας του οποίου η πρώτη και η δεύτερη θεμελιώδης μορφή είναι η
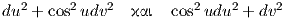
7. Αποδείξτε ότι τα σύμβολα του Cristoffel δίνονται από τον παρακάτω τύπο
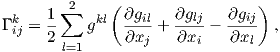
[1] M. Abate and F. Torena, Curves and Surfaces, Springer 2012.
[2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press 2010.
[3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall 1976.
[4] K. F. Gauss, Disqusitiones generales circa suporhcies curves, Comm. Soc. Göttingen Bd 6, 1823-1827.
[5] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, 2011. Μετάφραση 3ης εκδ. Dianusmatik�c Logism�c, Πανεπιστημιακές Εκδόσεις Κρήτης, 1992.
[6] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, 2007.
[7] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, 2013.
[8] A. Pressley, Elementary Differential Geometry, Second Edition, Springer 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.