
Σύνοψη
΄Ενας από τους κεντρικούς στόχους της διαφορικής γεωμετρίας είναι η εύρεση ενός φυσικού και αποτελεσματικού
τρόπου, προκειμένου να μετρηθεί η κύρτωση μη επίπεδων αντικειμένων (καμπύλες, επιφάνειες αλλά και άλλων).
ϒπάρχουν τουλάχιστον δύο τρόποι προκειμένου να οριστεί η καμπυλότητα μιας επιφάνειας. Εδώ θα
ακολουθήσουμε τη διαδικασία μέσω της απεικόνισης Gauss, δηλαδή ουσιαστικά μιας απεικόνισης που σε
κάθε σημείο μιας επιφάνειας αντιστοιχεί ένα μοναδιαίο κάθετο διάνυσμα στον αντίστοιχο εφαπτόμενο
χώρο.
Η προσέγγιση αυτή δεν είναι ο ιστορικός ορισμός που είχε δοθεί από τον Gauss, ο οποίος είναι λίγο πιο περίπλοκος. ΄Οπως και να έχει, η καμπυλότητα Gauss μιας επιφάνειας θα οριστεί ως ένα μέγεθος η μέτρηση του οποίου απαιτεί να "βλέπουμε" την επιφάνεια ως υποσύνολο του ℝ3. Το Θαυμαστό Θεώρημα (Theorema Egregium) του Gauss το οποίο θα δούμε στο επόμενο κεφάλαιο, αναφέρει ότι η καμπυλότητα είναι ένα μέγεθος που μπορεί να μετρηθεί (ή να αναγνωριστεί) από έναν παρατηρητή ο οποίος βρίσκεται επάνω στην επιφάνεια και όχι εκτός αυτής. Είναι δηλαδή ένα εσωτερικό μέγεθος της επιφάνειας. Με πιο απλο᾽ικό τρόπο, ο καπετάνιος ενός πλοίου που ταξιδεύει σε μεγάλη απόσταση, είναι δυνατόν να διαπιστώσει με δικές του μετρήσεις ότι η γη είναι σφαιρική και δεν χρειάζεται να επικοινωνήσει με πιλότο αεροπλάνου για τον σκοπό αυτό!
Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6].
Προαπαιτούμενη γνώση
Αναλυτική Γεωμετρία, Απειροστικός Λογισμός, Εισαγωγή στη Γραμμική ΄Αλγεβρα.
Ορισμός 5.1: ΄Εστω M μια κανονική επιφάνεια. Μια λεία απεικόνιση N : M → S2 ονομάζεται απεικόνιση Gauss της M εάν για κάθε p ∈ M η εικόνα N(p) έχει διάνυσμα θέσης ίσο με το μοναδιαίο διάνυσμα κάθετο της M στο p.
Εάν μια τέτοια απεικόνιση υπάρχει, τότε η επιφάνεια M ονομάζεται προσανατολίσιμη (orientable). Η επιφάνεια M εφοδιασμένη με μια τέτοια απεικόνιση Gauss ονομάζεται προσανατολισμένη (oriented) επιφάνεια.

Παραδείγματα.
1. ΄Εστω M = {(x,y,0) ∈ ℝ3 : x,y ∈ ℝ} το επίπεδο xy. Τότε μια απεικόνιση Gauss είναι η N(x,y,0) = (0,0,1).
2. ΄Εστω M = S2. Τότε μια απεικόνιση Gauss είναι η N = IdS2, όπου Id : S2 → S2,Id(p) = p η ταυτοτική
απεικόνιση της M.
3. ΄Εστω M = S1 × ℝ ο ορθός μοναδιαίος κύλινδρος. Τότε N(x,y,z) = (x,y,0) είναι μια απεικόνιση Gauss.
4. Η ταινία του Möbius (αναζητήστε τοπική παραμέτρηση και περιγραφή στη βιβλιογραφία) δεν επιδέχεται απεικόνιση Gauss, δηλαδή είναι μια μη προσανατολίσιμη επιφάνεια.
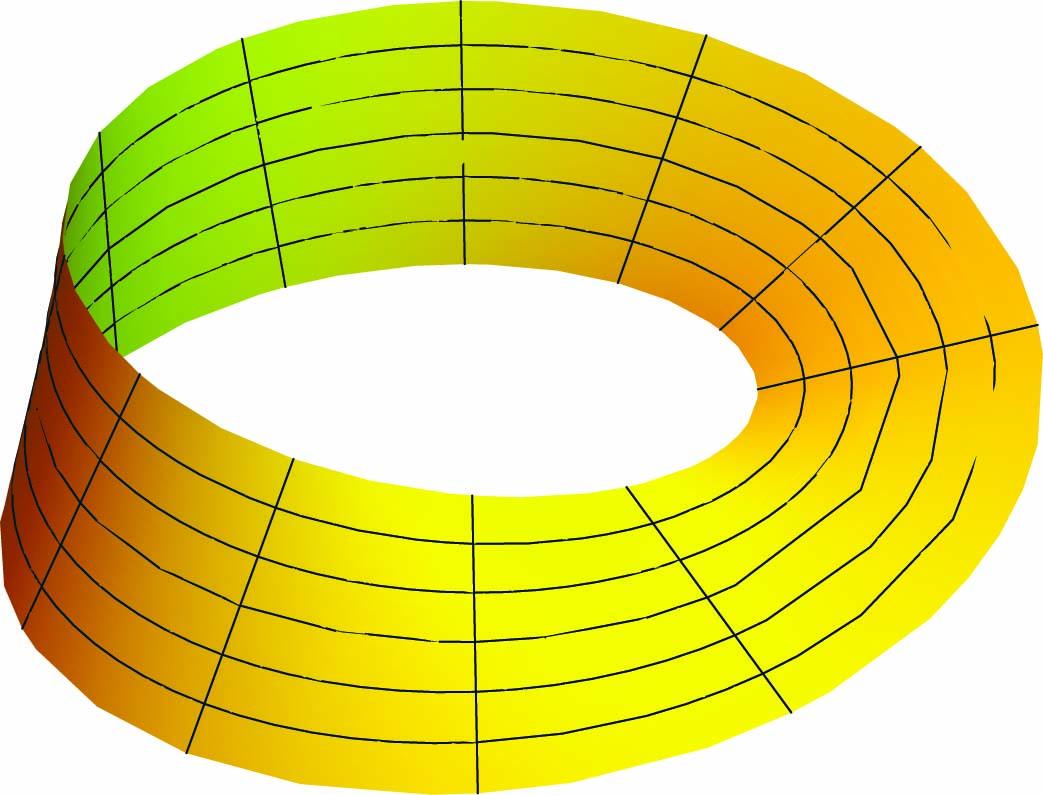
Παρατηρήσεις
 ) = p, τότε για κάθε q = X(u,υ) ∈ X(U) η απεικόνιση
) = p, τότε για κάθε q = X(u,υ) ∈ X(U) η απεικόνιση
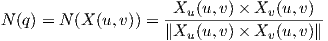
 TN(p)S2
(ισομορφισμός διανυσματικών χώρων). Μέσω αυτής της ταύτισης το διαφορικό dNp : TpM →
TN(p)S2 της απεικόνισης N τελικά γράφεται ως dNp : TpM → TpM.
TN(p)S2
(ισομορφισμός διανυσματικών χώρων). Μέσω αυτής της ταύτισης το διαφορικό dNp : TpM →
TN(p)S2 της απεικόνισης N τελικά γράφεται ως dNp : TpM → TpM.
Το προηγούμενο διαφορικό ουσιαστικά εκφράζει έναν τρόπο μεταβολής του διανύσματος N, άρα κατά κάποιο τρόπο, δίνει μια εικόνα για το σχήμα της επιφάνειας.
Ορισμός 5.2: ΄Εστω M μια κανονική προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2. Ο τελεστής σχήματος (shape operator) της M (απεικόνιση Weingarten) στο p ∈ M είναι η γραμμική απεικόνιση
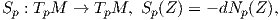
Το παρακάτω θεώρημα γενικεύει τον χαρακτηρισμό της ευθείας ως καμπύλης με μηδενική καμπυλότητα στις δύο διαστάσεις: μια συνεκτική επιφάνεια περιέχεται σε επίπεδο εάν και μόνο εάν ο τελεστής σχήματος της επιφάνειας είναι μηδενικός. ϒπενθυμίζουμε ότι ένα ανοικτό υποσύνολο U του επιπέδου είναι συνεκτικό, εάν δεν είναι ένωση μη κενών ανοικτών συνόλων, ξένων μεταξύ τους.
Θεώρημα 5.1: ΄Εστω M μια συνεκτική, προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2. Τότε ο τελεστής σχήματος Sp : TpM → TpM είναι ο μηδενικός τελεστής για κάθε p ∈ M, εάν και μόνο εάν η M είναι τμήμα ενός επιπέδου.
Απόδειξη. Αν η επιφάνεια M περιέχεται σε ένα επίπεδο, τότε η απεικόνιση Gauss είναι σταθερή, επομένως ο τελεστής σχήματος θα είναι ο μηδενικός τελεστής, δηλαδή Sp = -dNp = 0, για κάθε p ∈ M.
Αντίστροφα, σταθεροποιούμε ένα σημείο p ∈ M, έστω q ένα τυχαίο σημείο της M και γ : I → M μια καμπύλη τέτοια ώστε γ(0) = q και γ(1) = p. Τότε η απεικόνιση fq : I → ℝ με τιμή
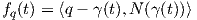
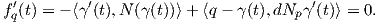
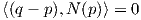
Παραδείγματα.
1. ΄Εστω M = S2,N(p) = p. Τότε Sp = -Id : TpS2 → TpS2.
2. ΄Εστω M το επίπεδο Oxy, N(x,y,0) = (0,0,1). Τότε N = σταθερή, άρα Sp = 0 για κάθε p ∈ M.
3. ΄Εστω M = S1 × ℝ ο ορθός μοναδιαίος κύλινδρος, N(x,y,z) = (x,y,0). Θα υπολογίσουμε τον τελεστή σχήματος Sp της M στο τυχαίο p = (x,y,z) ∈ M, βρίσκοντας τον αντίστοιχο πίνακα [Sp] της γραμμικής απεικόνισης Sp (ως προς κατάλληλη επιλογή της βάσης του TpM). Παρατηρούμε κατ′ αρχάς ότι TpM = span{(-y,x,0),(0,0,1)}. Τότε
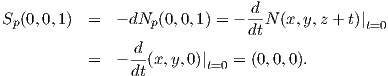
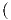 cos(t + t0),sin(t + t0),z
cos(t + t0),sin(t + t0),z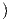 , όπου t0 ∈ ℝ είναι τέτοιο
ώστε (cost0,sint0) = (x,y). Τότε για την καμπύλη αυτή ισχύουν ότι
, όπου t0 ∈ ℝ είναι τέτοιο
ώστε (cost0,sint0) = (x,y). Τότε για την καμπύλη αυτή ισχύουν ότι 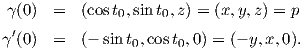
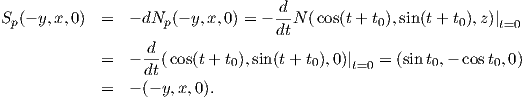
![( )
- 1 0
[Sp] = 0 0 .](02_chapter_0512x.png)
Πρόταση 5.1: ΄Εστω M μια κανονική, προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2 και p ∈ M. Τότε ο τελεστής σχήματος είναι αυτοσυζυγής τελεστής ως προς την πρώτη θεμελιώδη μορφή, δηλαδή ισχύει
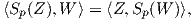
Απόδειξη. ΄Εστω X : U → M μια τοπική παραμέτρηση της M τέτοια ώστε X(0,0) = p και έστω N : X(U) → S2 η απεικόνιση Gauss στο X(U), η οποία δίνεται ως
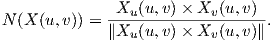
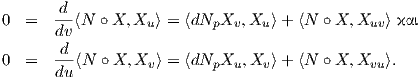
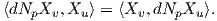
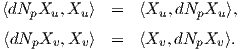
Σημείωση. Επειδή ο τελεστής σχήματος Sp είναι αυτοσυζυγής ο πίνακάς του είναι συμμετρικός, άρα είναι διαγωνιοποήσιμος με πραγματικές ιδιοτιμές.
Πόρισμα 5.1: ΄Εστω M κανονική και προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2,p ∈ M. Τότε υπάρχει ορθοκανονική βάση {Z1,Z2} ιδιοδιανυσμάτων της απεικόνισης Sp του εφαπτόμενου χώρου TpM τέτοια ώστε
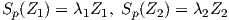
Ορισμός 5.3: ΄Εστω M μια κανονική και προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M → S2,p ∈ M. Η δεύτερη θεμελιώδης μορφή της M στο p είναι η συμμετρική, διγραμμική απεικόνιση
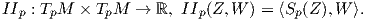
΄Οπως και στην περίπτωση της πρώτης θεμελιώδους μορφής, μάς ενδιαφέρει να βρούμε μια τοπική έκφραση της δεύτερης θεμελιώδους μορφής (δηλαδή έκφραση αυτής χρησιμοποιώντας μια τοπική παραμέτρηση της επιφάνειας).
΄Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2. ΄Εστω X : U ⊂ ℝ2 → M μια τοπική παραμέτρηση της M τέτοια ώστε X(0) = p ∈ M (είναι πάντα δυνατό να επιλέγουμε την απεικόνιση X με την ιδιότητα αυτή, απλώς κάνουμε μια μεταφορά).
Ως γνωστόν, ο εφαπτόμενος χώρος TpM TN(p)S2 παράγεται από τα διανύσματα Xu,Xυ. ΄Εστω
TN(p)S2 παράγεται από τα διανύσματα Xu,Xυ. ΄Εστω
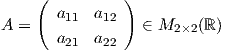
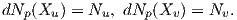 | (5.2) |
(Πράγματι, έστω  : I → U η καμπύλη
: I → U η καμπύλη  = (t,0) (δηλαδή ο άξονας x) του U ⊂ ℝ2 με
= (t,0) (δηλαδή ο άξονας x) του U ⊂ ℝ2 με 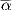 (0) = (0,0) και
(0) = (0,0) και
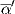 (0) = (1,0) ≡ e1. Τότε η α = X ∘
(0) = (1,0) ≡ e1. Τότε η α = X ∘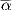 : I → M είναι μια καμπύλη στην επιφάνεια M, η οποία ικανοποιεί
α(0) = X
: I → M είναι μια καμπύλη στην επιφάνεια M, η οποία ικανοποιεί
α(0) = X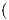
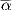 (0)
(0) = X(0,0) = p και α′(0) = X
= X(0,0) = p και α′(0) = X
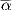 (0)
(0)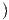 ⋅
⋅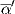 (0) = X(0,0)e1 = Xu. Συνεπώς, από τον ορισμό του
διαφορικού απεικόνισης μεταξύ επιφανειών έχουμε ότι
(0) = X(0,0)e1 = Xu. Συνεπώς, από τον ορισμό του
διαφορικού απεικόνισης μεταξύ επιφανειών έχουμε ότι
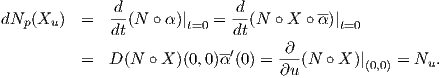
![A [dX ] = - [dN ],](02_chapter_0530x.png)
![[dX ] = (Xu,Xv )t, [dN ] = (Nu, Nv )t.](02_chapter_0531x.png)
Ορίζουμε τώρα τις συναρτήσεις e,f,g : U → ℝ από την ισότητα πινάκων
![( ) ( )
e f t t E F
f g = - [dN ][dX ] = A [dX ][dX ] = A F G .](02_chapter_0532x.png) | (5.4) |
Παραδοσιακά η δεύτερη θεμελιώδης μορφή γράφεται και
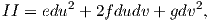
![[X X X ] [X X X ]
e = - ⟨Nu, Xu ⟩ = ⟨N, Xuu ⟩ =--u--v-uu- = √-u--v--uu-
∥Xu × Xv ∥ EG - F2
[XuXvXuv--] [XuXvXuv--]-
f = - ⟨Nu, Xv ⟩ = ⟨N, Xvu⟩ = ∥Xu × Xv∥ = √EG----F-2
[X X X ] [X X X ]
g = - ⟨Nv, Xv ⟩ = ⟨N, Xvv⟩ =--u--v--vv-= √--u-v--vv-.
∥Xu × Xv ∥ EG - F 2](02_chapter_0534x.png)
Οι θεμελιώδης μορφές προσδιορίζουν τοπικά την επιφάνεια. Πιο συγκεκριμένα ισχύει το θεμελιώδες θεώρημα των επιφανειών, σύμφωνα με το οποίο αν δίνονται τρείς συναρτήσεις E,F,G τάξης τουλάχιστον C3 και τρείς συναρτήσεις e,f,g τάξης τουλάχιστον C1, με πεδίο ορισμού ένα ανοικτό U υποσύνολο του ℝ2, έτσι ώστε να ισχύουν
τότε υπάρχει παραμέτρηση X : U → X(U) με X τάξης τουλάχιστον C3, τέτοια ώστε τα E,F,G e,f,g να είναι τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης αντιστοίχως, που ορίζονται από τη X. Η εικόνα X(U) είναι μονοσήμαντα ορισμένη, εκτός από τη θέση της στο χώρο.
΄Ενα από τα θεμελιώδη ερωτήματα της διαφορικής γεωμετρίας είναι με ποιόν τρόπο μπορούμε να μετρήσουμε την καμπυλότητα μιας επιφάνειας. Μια σημαντική παρατήρηση είναι ότι η καμπυλότητα μιας επιφάνειας (με όποιον τρόπο και αν αυτή οριστεί) δεν είναι σταθερή προς όλες τις διευθύνσεις. Για παράδειγμα, ο κυκλικός κύλινδρος ακτίνας r δεν καμπυλώνεται κατά τη διεύθυνση μιας γεννέτειρας, αλλά καμπυλώνεται κατά τη διεύθυνση των εφαπτομένων στις παράλληλες τομές του. Συνεπώς, είναι λογικό να πούμε ότι η καμπυλότητα του κυλίνδρου είναι μηδέν κατά τη διεύθυνση των γεννητόρων του, ενώ στη διεύθυνση των παραλλήλων τομών η καμπυλότητα ισούται με αυτή των ίδιων των τομών, δηλαδή 1∕r.
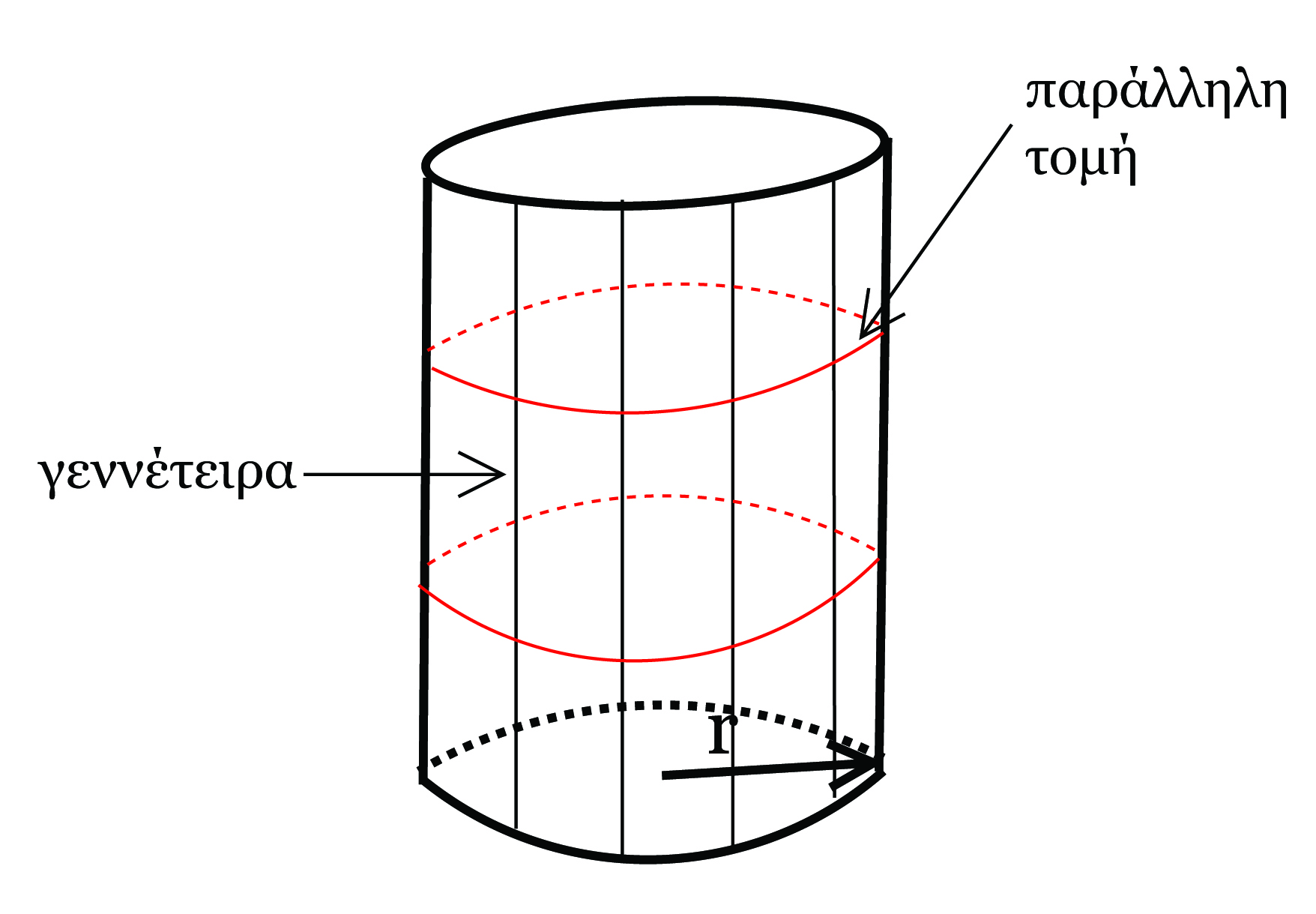
΄Αρα λοιπόν, ένας τρόπος μέτρησης της καμπυλότητας μιας επιφάνειας, είναι το να μελετηθούν κατάλληλες καμπύλες επί της επιφάνειας. Θα προσπαθήσουμε να κάνουμε την παραπάνω ιδέα πιο συγκεκριμένη.
΄Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2 και έστω γ : I → M μια
καμπύλη με παραμέτρηση ως προς το μήκος τόξου τέτοια, ώστε γ(0) = p, γ′(0) = Z ∈ TpM. Αναλύουμε τη
δεύτερη παράγωγο 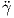 (0) στο p ως εξής:
(0) στο p ως εξής:
 (0)tan ∈ TpM είναι η εφαπτομενική συνιστώσα και
(0)tan ∈ TpM είναι η εφαπτομενική συνιστώσα και 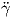 (0)norm ∈
(0)norm ∈ TpM
TpM ⊥ η κάθετη συνιστώσα
.
⊥ η κάθετη συνιστώσα
.
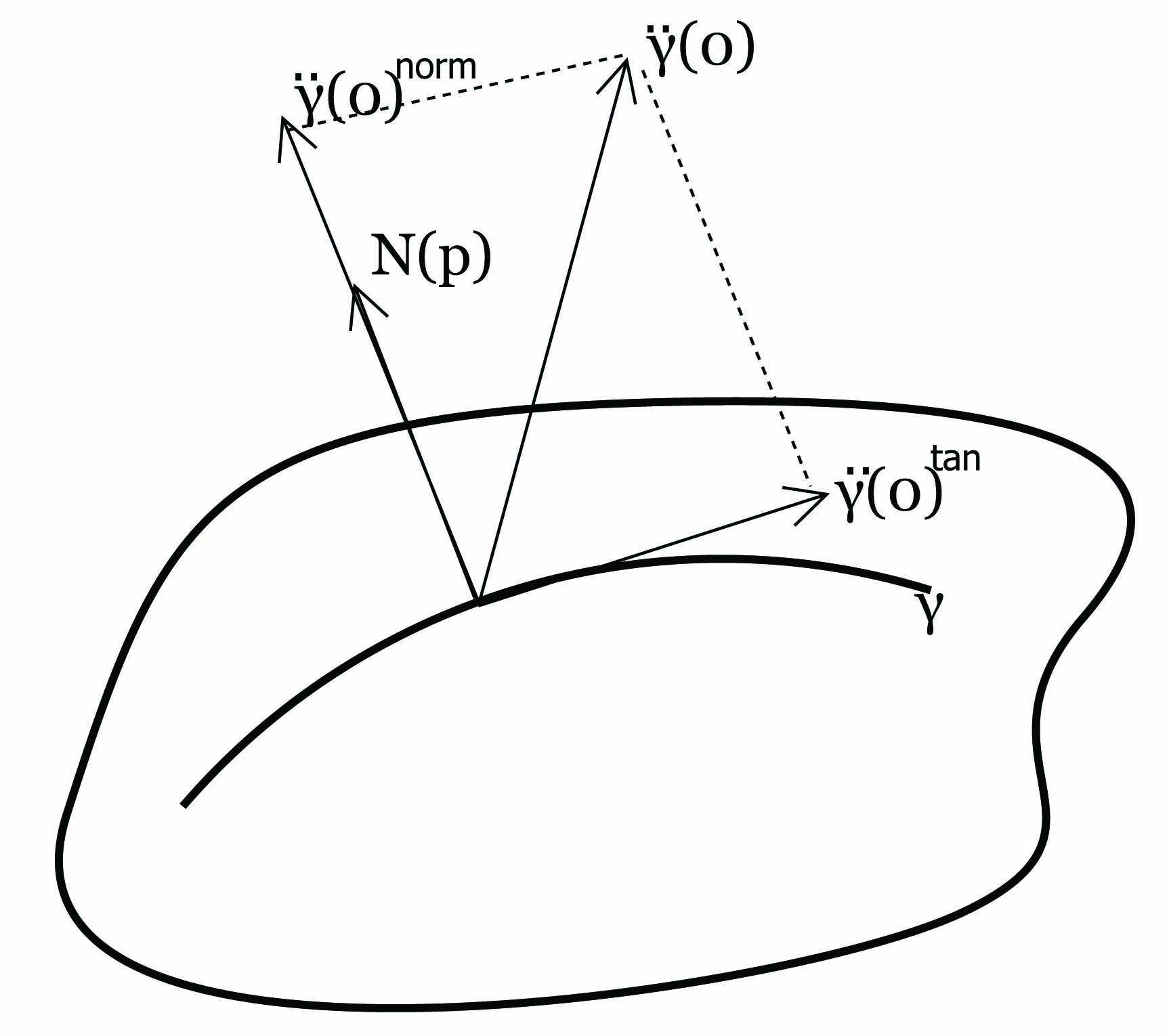
Το κάθετο διάνυσμα N(γ(s)) κατά μήκος της καμπύλης γ είναι κάθετο στην εφαπτομένη 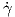 (s), συνεπώς για την
κάθετη συνιστώσα του διανύσματος
(s), συνεπώς για την
κάθετη συνιστώσα του διανύσματος 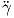 (0) ισχύει ότι
(0) ισχύει ότι
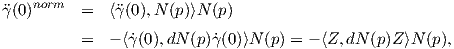
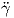 (0)norm του διανύσματος
(0)norm του διανύσματος 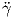 (0) καθορίζεται πλήρως από την τιμή
(0) καθορίζεται πλήρως από την τιμή 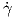 (0)
και τις τιμές της απεικόνισης Gauss κατά μήκος οποιασδήποτε καμπύλης, που διέρχεται από το σημείο
p, και με εφαπτόμενο διάνυσμα
(0)
και τις τιμές της απεικόνισης Gauss κατά μήκος οποιασδήποτε καμπύλης, που διέρχεται από το σημείο
p, και με εφαπτόμενο διάνυσμα 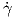 (0) = Z ∈ TpM. ΄Αρα ο ορισμός που δίνουμε στη συνέχεια είναι
καλός.
(0) = Z ∈ TpM. ΄Αρα ο ορισμός που δίνουμε στη συνέχεια είναι
καλός.
Ορισμός 5.5: ΄Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2,p ∈ M και Z ∈ TpM. Η κάθετη καμπυλότητα (normal curvature) κp(Z) της M στο p ως προς τη διεύθυνση του διανύσματος Z είναι ο αριθμός
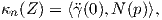
Προκειμένου να δώσουμε μια γεωμετρική περιγραφή της κάθετης καμπυλότητας, εργαζόμαστε ως εξής: Ως
καμπύλη στον χώρο ℝ3 η γ έχει καμπυλότητα κ(s) και κάθετο διάνυσμα Ñ(s) = 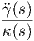 , συνεπώς
, συνεπώς 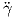 (0) = κ(0)Ñ(0).
Το διάνυσμα Ñ(0) αναλύεται ως
(0) = κ(0)Ñ(0).
Το διάνυσμα Ñ(0) αναλύεται ως
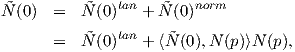
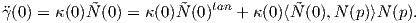
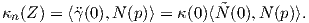
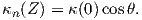
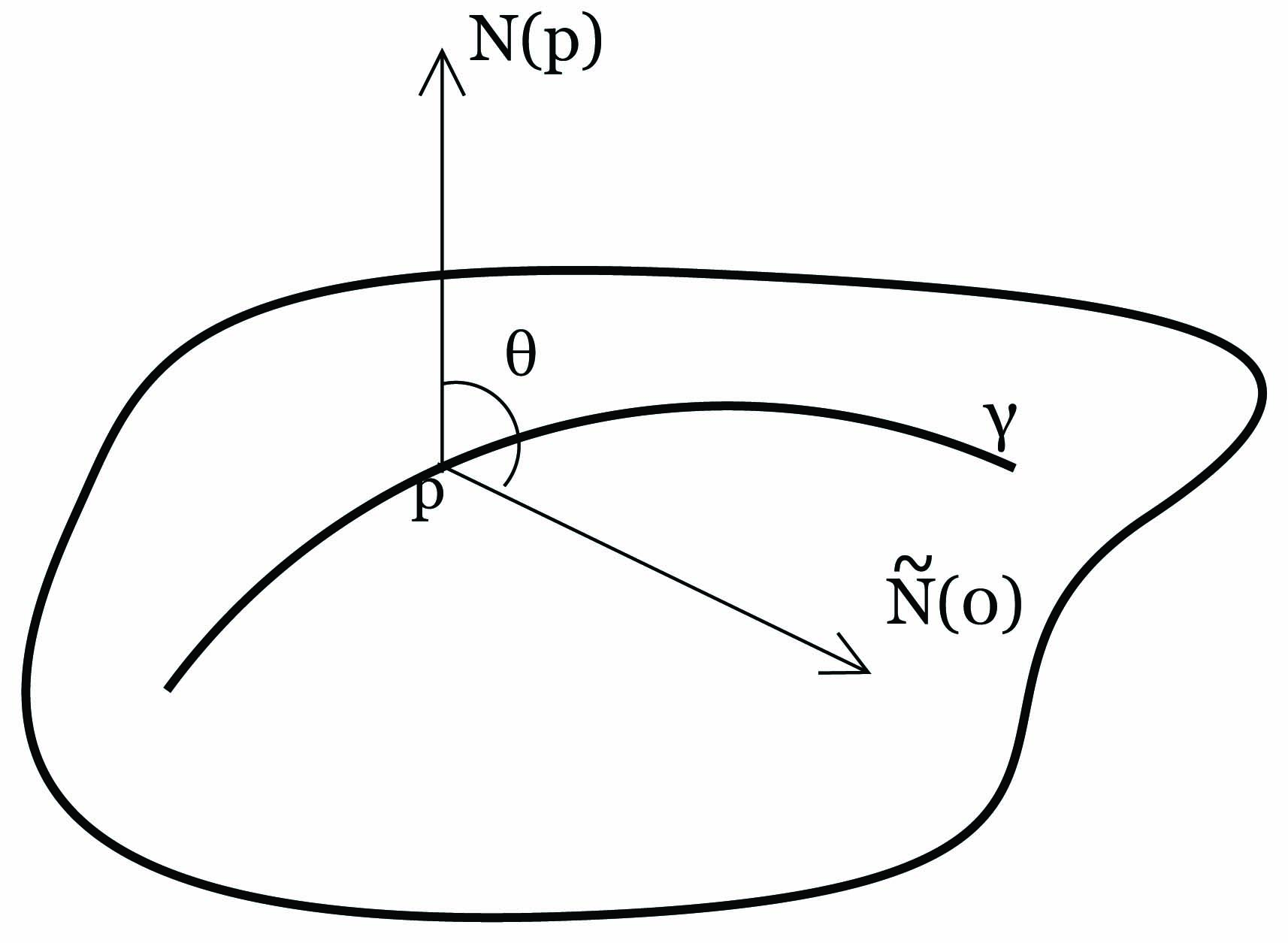
Επιπλέον, ισχύει |κp(Z)|≤ κ(0). Είναι λοιπόν σαφές ότι η κάθετη καμπυλότητα καθορίζει την "κύρτωση" της επιφάνειας, οπότε αναμένεται να σχετίζεται με τον τελεστή σχήματος, όπως φαίνεται στην παρακάτω πρόταση:
Πρόταση 5.2: (Θεώρημα Meusnier)
΄Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2,p ∈ M και
Z ∈ TpM. Τότε η κάθετη καμπυλότητα της M στο p ως προς τη διεύθυνση του διανύσματος Z ικανοποιεί
τη σχέση
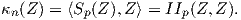
Απόδειξη. ΄Εστω γ μια καμπύλη με παράμετρο το μήκος τόξου, τέτοια ώστε γ(0) = p και 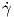 (0) = Z.
Κατά μήκος της καμπύλης αυτής το διάνυσμα N(γ(s)) είναι κάθετο στο εφαπτόμενο διάνυσμα
(0) = Z.
Κατά μήκος της καμπύλης αυτής το διάνυσμα N(γ(s)) είναι κάθετο στο εφαπτόμενο διάνυσμα 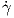 (s), δηλαδή
έχουμε
(s), δηλαδή
έχουμε
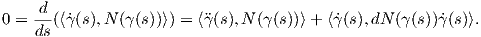
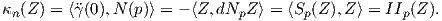
Θεωρούμε τώρα μια κανονική, προσανατολισμένη επιφάνεια M με απεικόνιση Gauss N : M → S2 και έστω
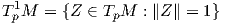
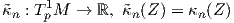
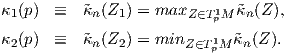
Θεώρημα 5.2: ΄Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2 και έστω p ∈ M. Τότε το διάνυσμα Z ∈ Tp1M είναι μια κύρια διεύθυνση στο p εάν και μόνο εάν το Z είναι ένα ιδιοδιάνυσμα του τελεστή σχήματος Sp : TpM → TpM.
Απόδειξη. ΄Εστω {Z1,Z2} μια ορθοκανονική βάση του TpM από ιδιοδιανύσματα του Sp, δηλαδή
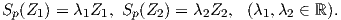
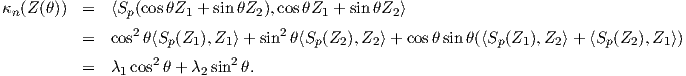
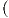 Z(θ)
Z(θ)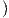 = IIp
= IIp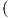 Z(θ),Z(θ)
Z(θ),Z(θ)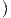 . Συνεπώς θα είναι λ1 = κ1,λ2 = κ2, άρα τελικά
. Συνεπώς θα είναι λ1 = κ1,λ2 = κ2, άρα τελικά
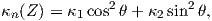
Συμπερασματικά, οι κύριες καμπυλότητες κ1,κ2 της M στο p είναι οι ιδιοτιμές του τελεστή σχήματος Sp : TpM → TpM, ο οποίος, όπως δείξαμε, είναι αυτοσυζυγής. Συνεπώς απο τη γραμμική άλγεβρα γνωρίζουμε ότι υπάρχει μια ορθοκανονική βάση απο ιδιοδιανύσματα {Z1,Z2} του TpM, ώστε ο πίνακας του τελεστή Sp ως προς αυτή τη βάση να είναι διαγώνιος, δηλαδή
![( )
[Sp] = κ1 0 .
0 κ2](02_chapter_0570x.png)
Ορισμός 5.6: ΄Εστω M προσανατολισμένη κανονική επιφάνεια του ℝ3 με απεικόνιση Gauss N : M → S2. Η καμπυλότητα Gauss (Gauss curvature) K και η μέση καμπυλότητα (mean curvature) H της M είναι οι συναρτήσεις
![K : M → ℝ, H : M → ℝ
1 1
K (p) = det[Sp] = κ1κ2, H (p) = 2tr[Sp ] = 2(κ1 + κ2).](02_chapter_0571x.png)
Μια επιφάνεια M ονομάζεται επίπεδη (flat), εάν K(p) = 0 για κάθε p ∈ M, και ελαχιστική (ή ελάχιστης έκτασης) (minimal), εάν H(p) = 0 για κάθε p ∈ M. (ϒπάρχει εξήγηση για τον όρο ελάχιστης έκτασης, αλλά δεν θα μας απασχολήσει αυτή την στιγμή).
Παράδειγμα 5.1: Στο παράδειγμα αυτό θα δείξουμε ότι για τυχαία επιφάνεια ισχύει η σχέση
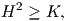
Γνωρίζουμε ότι
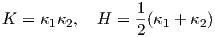
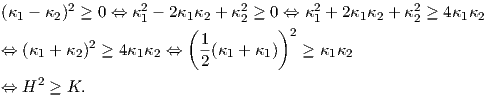
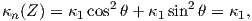
Ορισμός 5.7: ΄Ενα σημείο p ∈ M μιας κανονικής επιφάνειας του ℝ3 ονομάζεται
Ορισμός 5.8: Παράλληλη επιφάνεια της επιφάνειας M ονομάζεται η επιφάνεια M* η οποία παράγεται από την κίνηση κάθε σημείου της M κατά μήκος της καθέτου της M στο σημείο αυτό και σε σταθερή απόσταση α, α ∈ ℝ \{0}.
Σύμφωνα με τον παραπάνω ορισμό, μια παραμετρική εξίσωση της παράλληλης επιφάνειας θα είναι
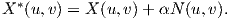
Πρόταση 5.3: Οι παράλληλες επιφάνειες M και M* έχουν στα αντίστοιχα σημεία τους, κάθετα διανύσματα τα οποία είτε ταυτίζονται, αν είναι ομόρροπα, είτε είναι αντίρροπα
Απόδειξη. ΄Εστω X : U → M μια παραμέτρηση της M. Τότε η X* = X(u,υ) + αN(u,υ) (α = ≠0) θα είναι η παραμέτρηση της M*. Από την σχέση αυτή παραγωγίζοντας ως προς u,υ έχουμε

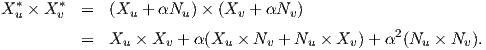
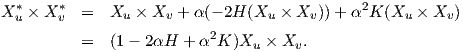
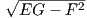 N, θα πάρουμε τελικά ότι
N, θα πάρουμε τελικά ότι
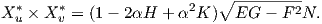
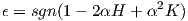
Από την παραπάνω πρόταση συμπεραίνουμε πως οι παράλληλες επιφάνειες έχουν στα αντίστοιχα σημεία τους
εφαπτόμενα επίπεδα παράλληλα. Για το λόγο αυτό η επιφάνεια M* λέγεται και παράλληλη επιφάνεια της M σε
απόσταση 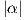 .
.
΄ϒστερα από τις παραπάνω διαπιστώσεις, για τις παράλληλες επιφάνειες, είναι φυσικό να αναρωτηθεί κανείς αν υπάρχουν σχέσεις που να συνδέουν τα θεμελιώδη μεγέθη των επιφανειών αυτών. Στη συνέχεια συμβολίζουμε με αστερίσκο τα θεμελιώδη ποσά της επιφάνειας M*.
Ισχύει η ακόλουθη πρόταση:
Πρόταση 5.4: Αν M και M* είναι δύο παράλληλες επιφάνειες τότε
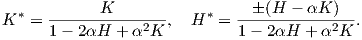
Τα ακόλουθα ενδιαφέροντα θεωρήματα οφείλονται στον Bonnet2:
Θεώρημα 5.3: (Bonnet) Αν η καμπυλότητα Gauss K της επιφάνειας M είναι σταθερή και θετική, τότε
υπάρχουν δύο παράλληλες επιφάνειες της M εκ των οποίων η μέση καμπυλότητα της μιας ισούται με 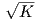 ∕2
και της άλλης με -
∕2
και της άλλης με -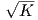 ∕2.
∕2.
Απόδειξη. Σύμφωνα με την υπόθεση είναι K > 0 και η καμπυλότητα αυτή είναι σταθερή. Γνωρίζουμε ότι η μέση καμπυλότητα της επιφάνειας M* παραλλήλου της M σε απόσταση α δίνεται από την σχέση
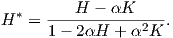 | (5.5) |
Ας θεωρήσουμε την επιφάνεια M1* που βρίσκεται σε απόσταση
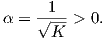 | (5.6) |
Τότε η σχέση (5.5) γίνεται
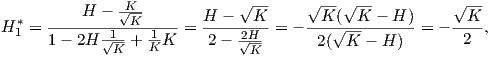
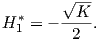
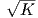 ∕2.
∕2.
Ας θεωρήσουμε τώρα την επιφάνεια M2* που βρίσκεται σε απόσταση
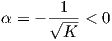
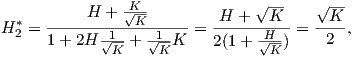
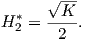
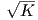 ∕2. ▄
∕2. ▄
Αντίστοιχα για τις καμπυλότητες Gauss εύκολα έχουμε (αποδείξτε το)
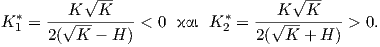
Θεώρημα 5.4: Αν η μέση καμπυλότητα H μιας επιφάνειας M είναι σταθερή και μη μηδενική, τότε υπάρχει παράλληλη επιφάνεια M* της M με σταθερή καμπυλότητα Gauss ίση με 4H2.
Απόδειξη. Γνωρίζουμε ότι αν M* είναι μια παράλληλη επιφάνεια της M σε απόσταση α, τότε η καμπυλότητα Gauss της M* δίνεται από την σχέση
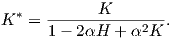 | (5.7) |
Θεωρούμε την επιφάνεια M* που βρίσκεται σε απόσταση
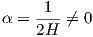 | (5.8) |
από τη M. Τότε η σχέση (5.7) γράφεται
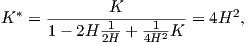
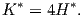
Η καμπυλότητα Gauss, η πιο σημαντική έννοια του παρόντος μαθήματος, δεν είχε οριστεί ιστορικά από τον Gauss με τον τρόπο που δώσαμε (ο οποίος είναι ιδιαιτέρως λειτουργικός). Η πραγματική γεωμετρική ερμηνεία της καμπυλότητας από τον Gauss περιγράφεται από την παρακάτω πρόταση:
Πρόταση 5.5: ΄Εστω M μια προσανατολισμένη κανονική επιφάνεια του ℝ3 με καμπυλότητα Gauss K(p)≠0 σε ένα σημείο της p ∈ M. ΄Εστω V η συνεκτική περιοχή του σημείου p όπου η καμπυλότητα K δεν αλλάζει πρόσημο. Τότε
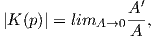
Θα εκφράσουμε τώρα την καμπυλότητα Gauss και τη μέση καμπυλότητα συναρτήσει των θεμελιωδών ποσών πρώτης και δεύτερης τάξης, χρησιμοποιώντας μια τοπική παραμέτρηση X : U → M της επιφάνειας M.
Θυμίζουμε ότι τα παραπάνω συνδέονται με την σχέση
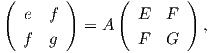
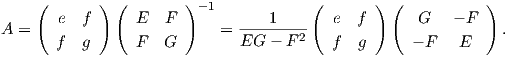
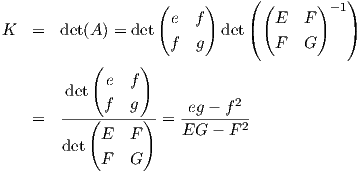
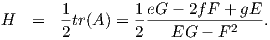
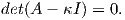
Αφού είναι γνωστή η μορφή των αij, μπορούμε να επανέλθουμε στο σύστημα (5.3) από το οποίο θα πάρουμε τις σχέσεις
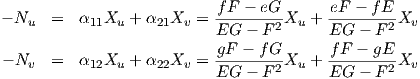
Αξίζει να σημειώσουμε εδώ ότι, αν είναι γνωστές οι K και H, οι κύριες καμπυλότητες μπορούν να υπολογιστούν ως οι ρίζες της δευτεροβάθμιας εξίσωσης
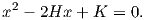
Παράδειγμα 5.2: ΄Εστω γ = (r,0,z) : I → ℝ3 μια λεία καμπύλη (με παράμετρο το μήκος τόξου) στο επίπεδο Oxz με r(u) > 0 και ṙ(u)2 + ż(u)2 = 1 για κάθε su ∈ I. Τότε η απεικόνιση X : I × ℝ → ℝ3 με τιμή
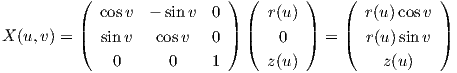
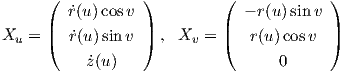
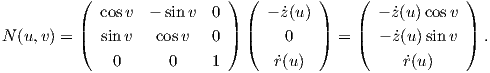
![( )
t ˙r(u)cosv ˙r(u)sinv ˙z(u)
[dX ] = (Xu, Xv) = - r(u)sin v r(u)cosv 0 ,](02_chapter_05112x.png)
![( ) ( )
E F = [dX ][dX ]t = 1 0
F G 0 r(u)2](02_chapter_05113x.png)
![( ) ( )
e f t - �r(u)˙z(u)+ �z(u)˙r(u) 0
f g = - [dN ][dX ]= 0 ˙z(u)r(u ) .](02_chapter_05114x.png)

Θα κάνουμε μια διερεύνηση της παραπάνω έκφρασης της καμπυλότητας. Ας πάρουμε την περίπτωση όπου η επιφάνεια M είναι η μοναδιαία σφαίρα S2, άρα r(u) = cosu,z(u) = sinu και έστω ότι -π∕2 < u < π∕2. Τότε E = 1,F = 0,G = cos2u και e = 1,f = 0,g = cos2u, άρα
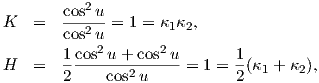
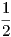 .
.
Ερχόμαστε πάλι στην γενική εξίσωση (⋆) και την γράφουμε ισοδύναμα ως τη διαφορική εξίσωση
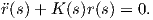
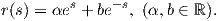
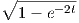 dt. Για τις επιλογές αυτές των συναρτήσεων
r,z : ℝ+ → ℝ παίρνουμε την παραμέτρηση
dt. Για τις επιλογές αυτές των συναρτήσεων
r,z : ℝ+ → ℝ παίρνουμε την παραμέτρηση 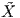 : ℝ+ × ℝ → M της ψευδοσφαίρας (είναι μια συμπαγής επιφάνεια με
σταθερή καμπυλότητα Gauss K = -1).
: ℝ+ × ℝ → M της ψευδοσφαίρας (είναι μια συμπαγής επιφάνεια με
σταθερή καμπυλότητα Gauss K = -1).
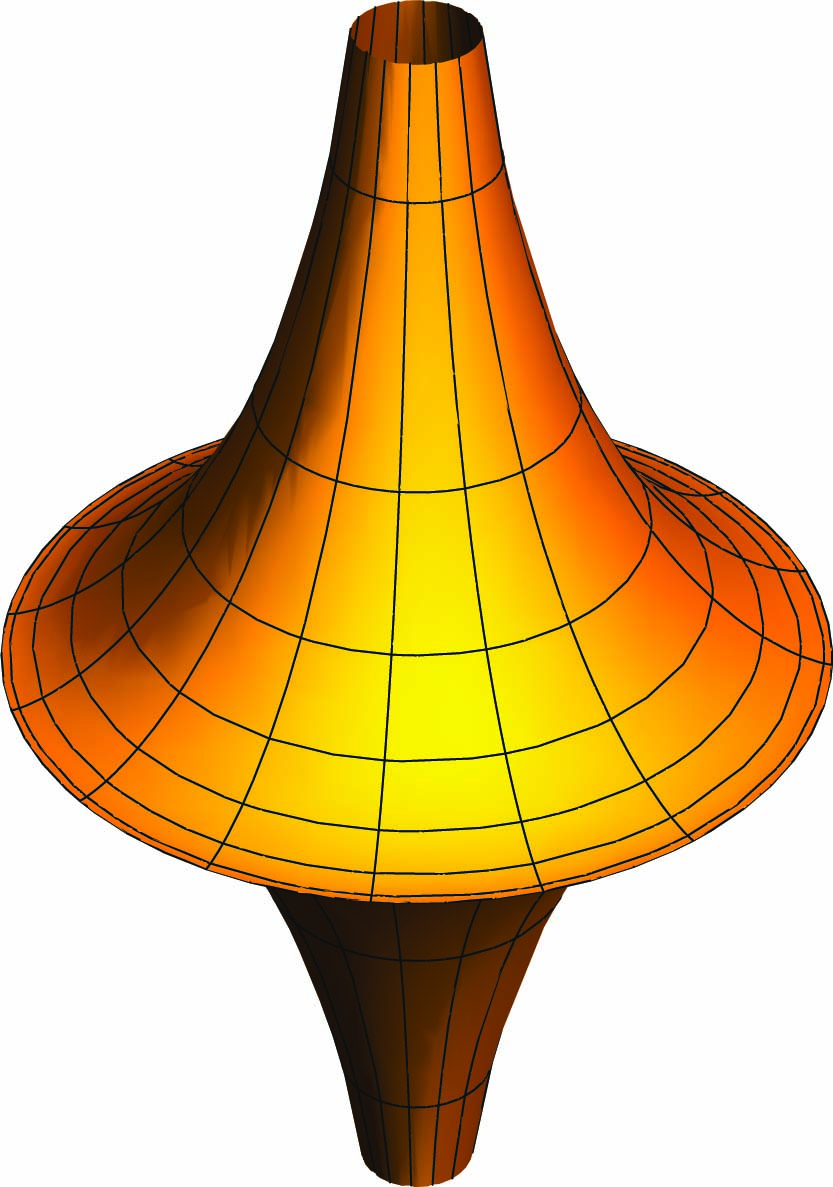
Η αντίστοιχη πρώτη θεμελιώδης μορφή είναι
![( ˜E F˜ ) ( 1 0 )
= [dX˜][dX˜]t = 2s .
˜F G˜ 0 e](02_chapter_05122x.png)
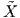
 s(u),υ
s(u),υ . Από τον κανόνα αλυσίδας είναι
Xu = su
. Από τον κανόνα αλυσίδας είναι
Xu = su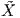 s = -
s = -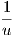
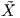 s, οπότε παίρνουμε την πρώτη θεμελιώδη μορφή της παραμέτρησης X
s, οπότε παίρνουμε την πρώτη θεμελιώδη μορφή της παραμέτρησης X
![( ) ( )
E F t 1 1 0
= [dX ][dX ] = u2- .
F G 0 1](02_chapter_05129x.png)
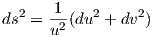
Κλείνουμε το κεφάλαιο αυτό με δύο ενδιαφέροντα αποτελέσματα ῾ὁλικού᾿᾿ χαρακτήρα για μια επιφάνεια M. Πρώτα θυμίζουμε το παρακάτω λήμμα από τον λογισμό συναρτήσεων πολλών μεταβλητών
Λήμμα 5.1: ΄Εστω U ανοικτό και συνεκτικό υποσύνολο του επιπέδου. Αν f : U → ℝ2 είναι μια λεία απεικόνιση τέτοια ώστε fx = fy = 0, τότε η f είναι η σταθερή απεικόνιση.
Θεώρημα 5.5: ΄Εστω M μια συνεκτική προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M → S2. Εάν κάθε σημείο p ∈ M είναι ομφαλικό, τότε η M είναι τμήμα είτε ενός επιπέδου είτε μιας σφαίρας.
Απόδειξη. ΄Εστω X : U → M μια παραμέτρηση της επιφάνειας M με το U να είναι συνεκτικό υποσύνολο του ℝ2. Επειδή κάθε σημείο του τμήματος της επιφάνειας X(U) είναι ομφαλικό, υπάρχει μια λεία απεικόνιση f : U → ℝ τέτοια ώστε ο τελεστής σχήματος να δίνεται ως
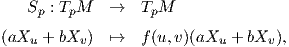
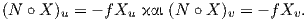
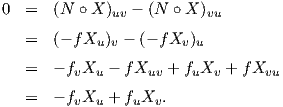
Αν f = 0, τότε ο τελεστής σχήματος είναι ο μηδενικός τελεστής, οπότε από Θεώρημα 5.1 η επιφάνεια περιέχεται σε ένα επίπεδο.
Αν f≠0, τότε ορίζουμε Y : U → ℝ3 με τιμή
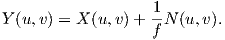
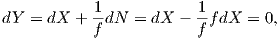
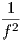 . Αυτό σημαίνει ότι το τμήμα της επιφάνειας X(U) περιέχεται σε μια σφαίρα
με κέντρο το Y και ακτίνα
. Αυτό σημαίνει ότι το τμήμα της επιφάνειας X(U) περιέχεται σε μια σφαίρα
με κέντρο το Y και ακτίνα 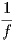 . Επειδή η M είναι συνεκτική, όλη η επιφάνεια θα περιέχεται στην ίδια σφαίρα.
▄
. Επειδή η M είναι συνεκτική, όλη η επιφάνεια θα περιέχεται στην ίδια σφαίρα.
▄
Θεώρημα 5.6: ΄Εστω M μια συμπαγής κανονική επιφάνεια. Τότε υπάρχει τουλάχιστον ένα σημείο p ∈ M με θετική καμπυλότητα Gauss K(p).
Απόδειξη. Θεωρούμε τη συνάρτηση f : M → ℝ με τύπο f(p) = ∥p∥2. Η f είναι συνεχής και επειδή η
επιφάνεια M είναι συμπαγής, τότε θα λαμβάνει μέγιστη και ελάχιστη τιμή. ΄Εστω p0 το σημείο της M, όπου
η f λαμβάνει τη μέγιστη τιμή. Επειδή f(p0) = ∥p0∥2, το σημείο p0 ∈ M έχει τη μέγιστη απόσταση από
την αρχή τον αξόνων. ΄Εστω r = ∥p0∥. Τότε η M περιέχεται σε μια σφαίρα Sr2 ακτίνας r.
Ισχυρισμός. K(p0) ≥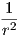 .
.
΄Εστω Z ∈ Tp0M και γ : I → M καμπύλη στην επιφάνεια M με γ(0) = p0 και γ′(0) = Z. Τότε η σύνθεση f ∘ γ : I → ℝ λαμβάνει και αυτή μέγιστη τιμή για t = 0. Συνεπώς θα έχουμε
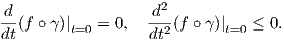
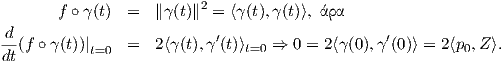
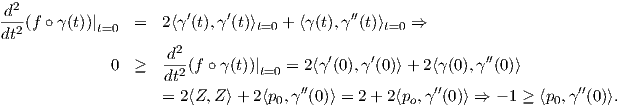
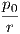 =
= 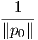 p0 είναι μοναδιαίο
διάνυσμα κάθετο στη M, υπολογίζουμε πρώτα την κάθετη καμπυλότητα ως
p0 είναι μοναδιαίο
διάνυσμα κάθετο στη M, υπολογίζουμε πρώτα την κάθετη καμπυλότητα ως 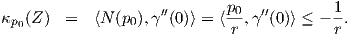
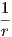 . ΄Αρα για την καμπυλότητα Gauss στο σημειο
p0 θα έχουμε ότι
. ΄Αρα για την καμπυλότητα Gauss στο σημειο
p0 θα έχουμε ότι
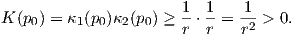
Πόρισμα 5.2: Δεν υπάρχουν συμπαγείς επιφάνειες στον ℝ3 με K ≤ 0. Ειδικότερα, δεν υπάρχουν συμπαγείς επιφάνειες του ℝ3 ελάχιστης έκτασης.
Το παρακάτω θεώρημα αποτελεί ένα σημαντικό αποτέλεσμα της ολικής διαφορικής γεωμετρίας.
Θεώρημα 5.7: (Liebmann) ΄Εστω M συμπαγής επιφάνεια με σταθερή καμπυλότητα Gauss K. Τότε η M
είναι μια σφαίρα ακτίνας 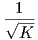 .
.
Λύση
Μια παραμέτρηση του παραβολοειδούς είναι η X(u,υ) = (u,υ,u2 + υ2). Θεωρούμε το μοναδιαίο κάθετο διάνυσμα που παίρνουμε από την παραμέτρηση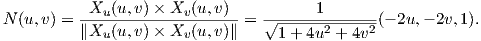
Παράδειγμα 5.4: Δίνεται η επιφάνεια του Enneper M με παραμέτρηση X : ℝ × ℝ+ → ℝ3
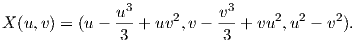
Λύση
Είναι Xu = (1 - u2 + υ2,2uυ,2u), Xυ = (2uυ,1 - υ2 + u2,-2υ),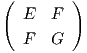 = [dX][dX]t, άρα
= [dX][dX]t, άρα
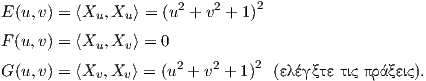
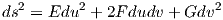
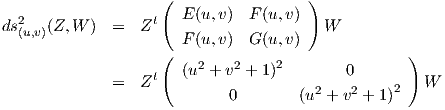
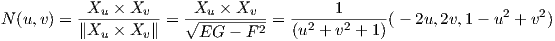
Για τα θεμελιώδη ποσά δεύτερης τάξης χρησιμοποιούμε τους τύπους
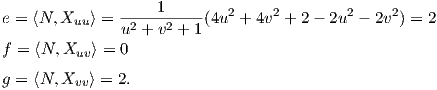
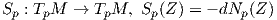
![( e f ) ( E F ) -1 ( e f ) ( G - F )
[Sp] = = ----1---2
f g F G EG - F f g - F E
( ) ( ) ( )
= ------1------ 2 0 1 0 = ------1------ 2 0 .
(u2 + v2 + 1)2 0 - 2 0 1 (u2 + v2 + 1)2 0 - 2](02_chapter_05157x.png)
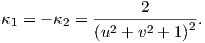
![-------4-----
K(u,v) = det[Sp ] = (u2 + v2 + 1)4](02_chapter_05159x.png)
![1- 1-
H = 2tr[Sp] = 2 (κ1 + κ2) = 0,](02_chapter_05160x.png)
Παράδειγμα 5.5: Θεωρούμε την κανονική επιφάνεια M ⊂ ℝ3 με (ολική) παραμέτρηση X : ℝ2 → M,X(u,υ) = (u,υ,u2 -υ2).
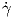 (0) = aXu + bXυ παίρνει πάντα
τιμές στο διάστημα [-2,2].
(0) = aXu + bXυ παίρνει πάντα
τιμές στο διάστημα [-2,2].Λύση
α) Είναι Xu = (1,0,2u),Xυ = (0,1,-2υ). ΄Αρα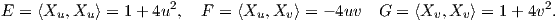
β) Μια απεικόνιση Gauss είναι
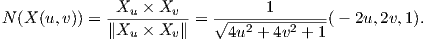
γ) ϒπολογίζουμε Xuu = (0,0,2),Xuυ = (0,0,0),Xυυ = (0,0,-2) άρα τα θεμελιώδη ποσά δεύτερης τάξης είναι
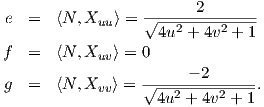
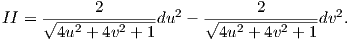
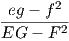 =
= 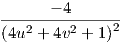 (μονίμως αρνητική).
(μονίμως αρνητική).
δ) Είναι ∥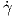 (0)∥2 = a2 + b2 το οποίο πρέπει να είναι μοναδιαίο διάνυσμα, άρα a = cosθ,b = sinθ. Συνεπώς, η
κάθετη καμπυλότητα στο σημείο p = γ(0) ως προς τη διεύθυνση του Z =
(0)∥2 = a2 + b2 το οποίο πρέπει να είναι μοναδιαίο διάνυσμα, άρα a = cosθ,b = sinθ. Συνεπώς, η
κάθετη καμπυλότητα στο σημείο p = γ(0) ως προς τη διεύθυνση του Z = 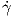 (0) είναι
(0) είναι
![2 2
κ (γ˙(0)) = II (Z,Z ) = 2cos-θ√ --sin-θ = 2cos 2θ ∈ [- 2,2].
γ(0) p 1](02_chapter_05170x.png)
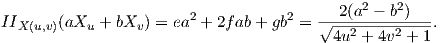
Παράδειγμα 5.6: Δείξτε ότι η μέση καμπυλότητα μιας κανονικής επιφάνειας στο σημείο p δίνεται από τη σχέση
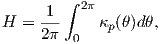
Λύση
Από τον τύπο του Euler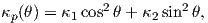
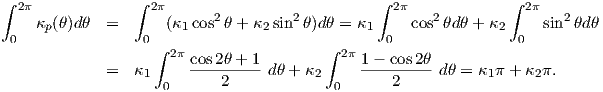
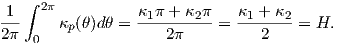
Παράδειγμα 5.7: ΄Εστω μια κανονική επιφάνεια M και p ∈ M. Αν w1,w2 ∈ TpM είναι γραμμικώς ανεξάρτητα διανύσματα τα οποία ικανοποιούν τις σχέσεις
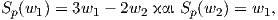
Λύση
Για να υπολογίσουμε τις κύριες καμπυλοτητες, πρέπει να υπολογίσουμε τις ιδιοτιμές του τελεστή σχήματος Sp : TpM → TpM. ΄Εστω λ μια ιδιοτιμή του Sp και u ένα ιδιοδιάνυσμα που αντιστοιχεί σε αυτήν. Επειδή τα w1,w2 είναι γραμμικώς ανεξάρτητα, θα έχουμε u = aw1 + bw2. Επειδή Sp(u) = λu και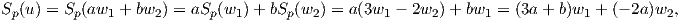
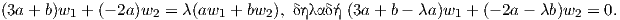
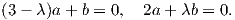 | (5.9) |
Επειδή το u είναι ένα ιδιοδιάνυσμα, θα είναι u≠0, οπότε
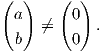
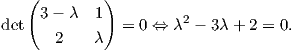
Παράδειγμα 5.8: Δίνεται μια κανονική επιφάνεια M και ο εφαπτόμενος χώρος της TpM στο σημείο p ∈ M. Αν υποθέσουμε ότι w1,w2 ∈ TpM είναι γραμμικώς ανεξάρτητα διανύσματα, τότε ισχύουν οι σχέσεις
Λύση
Τα διανύσματα w1,w2 αποτελούν βάση του εφαπτόμενου χώρου TpM, οπότε μπορούμε να γράψουμε ότι
![( )
λ1 λ2
[Sp] = μ1 μ2 .](02_chapter_05183x.png)
![K (p) = det([S ]) = λ μ - λ μ
p 1 2 2 1
H(p) = 1tr([Sp]) = 1(λ1 + μ2 ),
2 2](02_chapter_05184x.png)
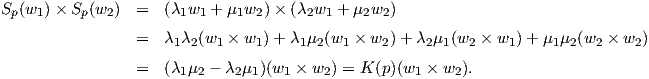
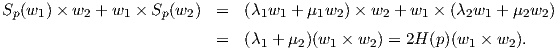
1. ϒπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της επιφάνειας X(u,υ) = (u + υ,u-υ,uυ) στο σημείο (2,0,1.)
2. ΄Εστω U ανοικτό υποσύνολο του ℝ3 και q ∈ ℝ μια κανονική τιμή της διαφορίσιμης συνάρτησης f : U → ℝ.
Αποδείξτε ότι η κανονική επιφάνεια M = f-1(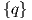 ) του ℝ3 είναι προσανατολίσιμη.
) του ℝ3 είναι προσανατολίσιμη.
3. ϒπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της σφαίρας
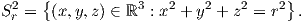
4. Δίνεται η επιφάνεια του Enneper με παραμέτρηση X : ℝ × ℝ+ → ℝ3
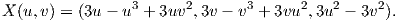

5. ϒπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της αλυσοειδούς επιφάνειας (catenoid) M με παραμέτρηση X : ℝ × ℝ+ → ℝ3
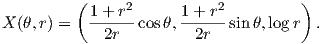
Βρείτε μια εξίσωση της μορφής f(x,y,z) = 0 που να περιγράφει τη M.

6. ΄Εστω X,Y : ℝ2 → ℝ3 με X(u,υ) = 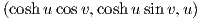 Y (u,υ) =
Y (u,υ) = 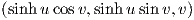 οι
παραμετρήσεις της αλυσοειδούς και ελικοειδούς επιφάνειας αντίστοιχα. ϒπολογίστε τις κύριες καμπυλότητες κ1,κ2
των X,Y.
οι
παραμετρήσεις της αλυσοειδούς και ελικοειδούς επιφάνειας αντίστοιχα. ϒπολογίστε τις κύριες καμπυλότητες κ1,κ2
των X,Y.

7. Αποδείξτε ότι η δεύτερη θεμελιώδης μορφή μιας κανονικής επιφάνειας M του ℝ3 παραμένει αναλλοίωτη κάτω από στερεές κινήσεις.
8. ΄Εστω γ : ℝ → ℝ3 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου και με καμπυλότητα μη
μηδενική. ΄Εστω 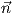 ,
,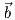 τα διανύσματα της πρώτης καθέτου και της δεύτερης καθέτου της γ αντίστοιχα.
Για r > 0 υποθέτουμε ότι ο σωλήνας (tube) M ακτίνας r περί τη γ με παραμέτριση X : ℝ2 → ℝ3,
X(s,θ) = γ(s) + r(cosθ ⋅
τα διανύσματα της πρώτης καθέτου και της δεύτερης καθέτου της γ αντίστοιχα.
Για r > 0 υποθέτουμε ότι ο σωλήνας (tube) M ακτίνας r περί τη γ με παραμέτριση X : ℝ2 → ℝ3,
X(s,θ) = γ(s) + r(cosθ ⋅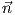 (s) + sinθ ⋅
(s) + sinθ ⋅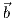 (s)) είναι μια κανονική επιφάνεια του ℝ3. ϒπολογίστε την καμπυλότητα
Gauss K της επιφάνειας M ως προς s,θ,r,k(s) και τ(s).
(s)) είναι μια κανονική επιφάνεια του ℝ3. ϒπολογίστε την καμπυλότητα
Gauss K της επιφάνειας M ως προς s,θ,r,k(s) και τ(s).
9. ΄Εστω X : U → ℝ3 παραμέτρηση μιας επιφάνειας M του ℝ3 με απεικόνιση Gauss N : M → S2 και με κύριες
καμπυλότητες k1 = 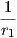 ,k2 =
,k2 = 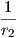 . ΄Εστω r ∈ ℝ τέτοιο ώστε η Xr : U → ℝ3 με Xr(u,υ) = X(u,υ) + rN(u,υ) να
είναι παραμέτρηση μιας επιφάνειας του ℝ3. Αποδείξτε ότι οι κύριες καμπυλότητες της Xr ικανοποιούν τις σχέσεις
k1(r) =
. ΄Εστω r ∈ ℝ τέτοιο ώστε η Xr : U → ℝ3 με Xr(u,υ) = X(u,υ) + rN(u,υ) να
είναι παραμέτρηση μιας επιφάνειας του ℝ3. Αποδείξτε ότι οι κύριες καμπυλότητες της Xr ικανοποιούν τις σχέσεις
k1(r) = 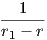 και k2(r) =
και k2(r) = 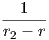 .
.
10. ϒπολογίστε την καμπυλότητα Gauss της επιφάνειας με παραμέτρηση X : ℝ × ℝ → M,
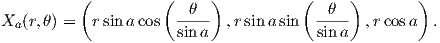
11. Εφοδιάζουμε τους χώρους ℝ2 και ℝ4 με τα κανονικά εσωτερικά γινόμενα. Αποδείξτε ότι η παραμέτρηση
X : ℝ2 → ℝ4 με X(u,υ) = 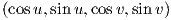 του συμπαγούς δακτυλίου (torus) M στον ℝ4 είναι
ισομετρική. Τί μας λέει αυτό για την καμπυλότητα Gauss του M;
του συμπαγούς δακτυλίου (torus) M στον ℝ4 είναι
ισομετρική. Τί μας λέει αυτό για την καμπυλότητα Gauss του M;
12. ΄Εστω α(s) μια καμπύλη μοναδιαίας ταχύτητα με στρέψη τ(s)≠0 και διάνυσμα δεύτερης κάθετης B(s). Θεωρούμε την επιφάνεια M με τοπική παραμέτρηση
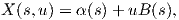
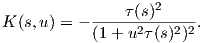
13. (a) Εξηγήστε (χωρίς ιδιαίτερους υπολογισμούς) γιατί οι παρακάτω επιφάνειες δεν είναι ανα δύο τοπικά ισομετρικές
(b) Δώστε παράδειγμα επιφάνειας με σταθερή καμπυλότητα Gauss K = -1. Γράψτε την πρώτη θεμελιώδη μορφή αυτής.
14. Αναζητήστε στη βιβλιογραφία μια απόδειξη του Θεωρήματος 5.7.
[1] M. Abate and F. Torena, Curves and Surfaces, Springer 2012.
[2] C. Bär Elementary Differential Geometry, Cambridge Univ. Press 2010.
[3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall 1976.
[4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, 2007.
[5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, 2013.
[6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.