Κεφάλαιο 11
Επιφάνειες σταθερής καμπυλότητας Gauss

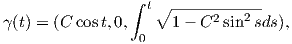
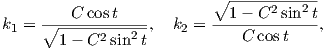
Σύνοψη
Παρουσιάζουμε χωρίς απόδειξη την ταξινόμηση των επιφανειών του ℝ3 με σταθερή καμπυλότητα Gauss, θετική, μηδέν, ή αρνητική. Εξετάζουμε χωριστά τις περιπτώσεις των κλειστών και των μη κλειστών επιφανειών.

Προαπαιτούμενη γνώση
Στοιχειώδης θεωρία επιφανειών.

Μια ενδιαφέρουσα περιοχή της στοιχειώδους διαφορικής γεωμετρίας είναι η ολική θεωρία των επιφανειών (global theory of surfaces). Στη θεωρία αυτή ανήκουν πολλά σημαντικά θεωρήματα, οι αποδείξεις πολλών από αυτά είναι ιδιαίτερα δύσκολες, επειδή απαιτούν συνδυασμούς τεχνικών, τόσο από τη διαφορική γεωμετρία όσο και τη μαθηματική ανάλυση. Ως εκ τούτου, πολλά από τα αποτελέσματα αυτά αποδείχτηκαν αρκετά χρόνια μετά την πλήρη ανάπτυξη της θεωρίας των επιφανειών από τον Gauss. Μερικοί μαθηματικοί που συνεισέφεραν στον χώρο αυτό είναι οι D. Hilbert, J. Hadamard, J.J. Stoker, κ.ά.

΄Ενα τυπικό παράδειγμα θεωρήματος της ολικής θεωρίας επιφανειών είναι το Θεώρημα των Gauss-Bonnet, το οποίο αποδείξαμε στο Κεφάλαιο 10. Εδώ θα παρουσιάσουμε χωρίς απόδειξη την ταξινόμηση των κλειστών επιφανειών του ℝ3, οι οποίες έχουν σταθερή καμπυλότητα Gauss. Ως κλειστή επιφάνεια εννούμε μια κανονική επιφάνεια, η οποία είναι, τοπολογικά, κλειστό υποσύνολο του ℝ3. Επίσης, θυμίζουμε ότι με τον όρο σταθερή καμπυλότητα Gauss, εννούμε ότι η καμπυλότητα Gauss (ως συνάρτηση) λαμβάνει ταυτοτικά την ίδια τιμή σε κάθε σημείο της επιφάνειας.

Γνωρίζουμε μερικά παραδείγματα τέτοιων επιφανειών, όπως το επίπεδο, η σφαίρα και ο κύλινδρος. Τίθεται λοιπόν το φυσικό ερώτημα, κατά πόσον υπάρχουν και άλλες επιφάνειες με σταθερή καμπυλότητα Gauss. Η απάντηση είναι ότι για την περίπτωση των κλειστών επιφανειών, οι επιλογές δεν είναι ιδιαίτερα πολλές. Για τις μη κλειστές επιφάνειες το πρόβλημα ανάγεται στην ταξινόμηση των επιφανειών εκ περιστροφής με σταθερή καμπυλότητα Gauss. Για αναλυτικές αποδείξεις των θεωρημάτων του παρόντος κεφαλαίου παραπέμπουμε στα βιβλία [1], [2] και [8].

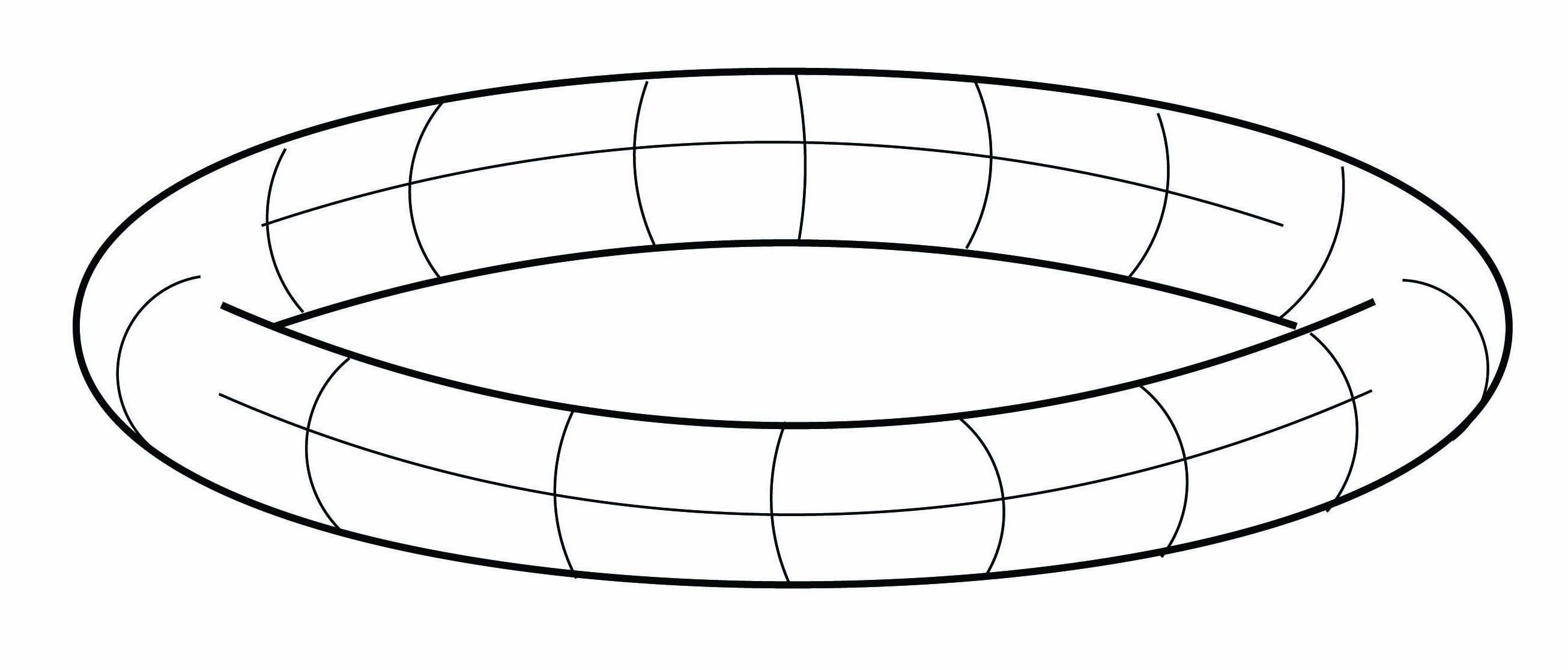
11.1 Κλειστές επιφάνειες σταθερής καμπυλότητας Gauss

11.1.1 Επιφάνειες με θετική καμπυλότητα Gauss

΄Εστω M μια κλειστή κανονική επιφάνεια με σταθερή καμπυλότητα Gauss. Εάν η M είναι συμπαγής, τότε σύμφωνα με το Θεώρημα 7.3 (Liebmann) που έχουμε αποδείξει στο Κεφάλαιο 7, η M είναι μια σφαίρα. Η υπόθεση της συμπάγειας στο Θεώρημα του Liebmann είναι απαραίτητη, όπως φαίνεται στο παρακάτω παράδειγμα.

Παράδειγμα 11.1: ΄Εστω C > 1 σταθερά και έστω M ⊂ ℝ3 η επιφάνεια εκ περιστροφής, η οποία προκύπτει περιστρέφοντας την καμπύλη γ : (-arcsin(1∕C),arcsin(1∕C)) → ℝ3,

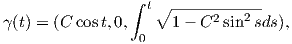
∫ t∘ ------------ γ (t) = (C cost,0, 1- C2 sin2 sds), 0
περί τον άξονα z. Τότε οι κύριες καμπυλότητες της M είναι
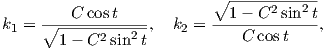
∘ ------------ ----C-cost---- --1--C2-sin2t- k1 = ∘1----C2-sin2-t, k2 = C cost ,
συνεπώς K = k1k2 = 1. Επιπλέον, επειδή C > 1, η επιφάνεια M δεν περιέχει ομφαλικά σημεία, συνεπώς η M δεν περιέχεται σε κάποια σφαίρα. Επίσης, η M δεν είναι συμπαγής ούτε κλειστή στον ℝ3.

Σχήμα 11.1: Μη συμπαγής επιφάνεια με σταθερή καμπυλότητα Gauss.

Είναι δυνατόν να αποδειχθεί ότι, κάθε κλειστή επιφάνεια της οποίας η καμπυλότητα Gauss είναι κάτω φραγμένη από μια θετική σταθερά, είναι συμπαγής. Συγκεκριμένα, ισχύει το εξής:

Θεώρημα 11.1: ΄Εστω M μια κανονική, κλειστή επιφάνεια, τέτοια ώστε να ισχύει

K ≥ δ > 0.
Τότε η M είναι συμπαγής.

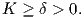
Συνεπώς, λόγω του Θεωρήματος Liebmann προκύπτει το εξής ισχυρότερο θεώρημα:

Θεώρημα 11.2: Οι μόνες κλειστές επιφάνειες του ℝ3 με σταθερά θετική καμπυλότητα Gauss, είναι οι σφαίρες.

11.1.2 Επιφάνειες με μηδενική καμπυλότητα Gauss

Το πρόβλημα της ταξινόμησης των κλειστών επιφανειών με καμπυλότητα Gauss ταυτοτικά μηδέν, δεν είναι εύκολο. Γνωρίζουμε δύο τέτοιες κλάσεις επιφανειών, τα επίπεδα και τους γενικευμένους κυλίνδρους. Το αποτέλεσμα είναι ότι αυτές είναι οι μόνες. Συγκεκριμένα, ισχύει το εξής:

Θεώρημα 11.3: (Hartman-Nirenberg). ΄Εστω M ⊂ ℝ3 μια κλειστή επιφάνεια με καμπυλότητα Gauss ταυτοτικά μηδέν. Τότε η M είναι είτε ένα επίπεδο, είτε ένας (γενικευμένος) κύλινδρος.

Για την απόδειξη του θεωρήματος αυτού παραπέμπουμε στα βιβλία [1], [2] και στις εργασίες [3], [4] και [5].

Η υπόθεση της κλειστότητας του Θεωρήματος των Hartman-Nirenberg είναι απαραίτητη, όπως φαίνεται από στο παρακάτω παράδειγμα.

Παράδειγμα 11.2: Θεωρούμε την επιφάνεια

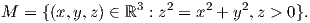
3 2 2 2 M = {(x,y,z) ∈ ℝ : z = x + y ,z > 0}.
Η επιφάνεια αυτή είναι το άνω τμήμα ενός κυκλικού κώνου, ο οποίος προκύπτει ως επιφάνεια εκ περιστροφής της καμπύλης γ : (0,+∞) → ℝ, γ(t) = (t,0,t). ΄Ενας υπολογισμός δίνει ότι K ≡ 0 και H(x,y,z) = 1 z. Κάθε σημείο της επιφάνειας M είναι ένα παραβολικό σημείο, συνεπώς η M δεν είναι τμήμα κάποιου επιπέδου. Επιπλέον, από κάθε παραβολικό σημείο της M διέρχεται ένα και μοναδικό ευθύγραμμο τμήμα, το οποίο να ανήκει στη M (βλ. ΄Ασκηση 3), άρα το τμήμα αυτό είναι ένας γεννήτορας του κώνου. Συνεπώς, εάν η επιφάνεια M ήταν τμήμα ενός κυλίνδρου, οι γεννήτορες αυτής θα ήταν παράλληλοι μεταξύ τους, κάτι που δεν ισχύει.

11.1.3 Επιφάνειες με αρνητική καμπυλότητα Gauss

Το κεντρικό αποτέλεσμα εδώ είναι το παρακάτω Θεώρημα του Hilbert, το οποίο αναφέρει ότι τέτοιες κλειστές επιφάνειες δεν υπάρχουν.

Θεώρημα 11.4: (Hilbert). Δεν υπάρχουν κλειστές επιφάνειες στον ℝ3, για τις οποίες η καμπυλότητα Gauss να είναι σταθερά αρνητική.

Το θεώρημα αυτό αποδείχτηκε αρχικά από τον Hilbert στην εργασία [4] και μια διαφορετική απόδειξη δόθηκε από τον Holmgren στην εργασία [5]. Για αναλυτικές αποδείξεις παραπέμπουμε στα βιβλία [1], [2] και [8].

11.2 Μη κλειστές επιφάνειες σταθερής καμπυλότητας Gauss

Ισχύει το εξής θεώρημα.

Θεώρημα 11.5: (Minding). Εάν δύο κανονικές επιφάνειες έχουν τις ίδιες σταθερές καμπυλότητες Gauss, τότε είναι τοπικά ισομετρικές.

Ως αποτέλεσμα του θεωρήματος αυτού, το πρόβλημα της ταξινόμησης των επιφανειών με σταθερή καμπυλότητα Gauss, ανάγεται στο πρόβλημα της ταξινόμησης των εκ περιστροφής επιφανειών με σταθερή καμπυλότητα Gauss. Το πρόβλημα αυτό είναι σαφώς απλούστερο. Ως γνωστόν, μια τοπική παραμέτρηση για μια επιφάνεια εκ περιστροφής περί τον άξονα z, έχει τη μορφή

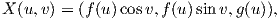
X (u,v) = (f (u)cosv,f(u)sinv,g(u)),
όπου f > 0 και f′2 + g′2 = 1. Τα θεμελιώδη ποσά πρώτης τάξης για την παραμέτρηση αυτή είναι E = 1,F = 0 και G = f(u)2, συνεπώς (βλ. Κεφάλαιο 6) η καμπυλότητα Gauss δίνεται από την σχέση
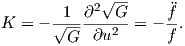
√ -- -1-∂2--G- ?f- K = - √G ∂u2 = - f.
Η παραπάνω διαφορική εξίσωση παίρνει τη μορφή
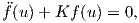
? f(u)+ Kf (u ) = 0,
η οποία για K σταθερή μπορεί σχετικά εύκολα να διερευνηθεί (βλ. για παράδειγμα [8] και [9]) και τελικά προκύπτει το εξής:

Θεώρημα 11.6: Κάθε επιφάνεια με σταθερή καμπυλότητα Gauss είναι τοπικά ισομετρική με ένα επίπεδο, μια σφαίρα ή μια ψευδοσφαίρα.

Σύμφωνα λοιπόν με το παραπάνω θεώρημα, η γεωμετρία που ορίζεται πάνω σε επιφάνειες μηδενικής καμπυλότητας Gauss ταυτίζεται με τη γεωμετρία του Ευκλείδειου επιπέδου, η γεωμετρία που ορίζεται πάνω σε επιφάνειες σταθερά θετικής καμπυλότητας Gauss ταυτίζεται με τη γεωμετρία της σφαίρας και τέλος, η γεωμετρία που ορίζεται πάνω σε επιφάνειες σταθερά αρνητικής καμπυλότητας Gauss, ταυτίζεται με τη γεωμετρία της ψευδοσφαίρας.

Για την περίπτωση όπου η καμπυλότητα Gauss είναι μηδέν, η επιφάνεια ονομάζεται αναπτυκτή (developable). Μια τέτοια επιφάνεια μπορεί να κατασκευαστεί με κύρτωση ενός επίπεδου φύλλου χαρτιού.

Κλείνοντας το σύντομο αυτό κεφάλαιο (αλλά και το παρόν βιβλίο), αξίζει να αναφέρουμε και μια άλλη περιοχή της ολικής διαφορικής γεωμετρίας, η οποία είναι η μελέτη των επιφανειών του ℝ3 με σταθερή μέση καμπυλότητα. Η θεωρία αυτή συνδέεται ιστορικά με ένα πρόβλημα του J. Plateau (~ 1800), ο οποίος μέσω μελέτης σαπουνόφουσκων προσπαθούσε να βρει επιφάνειες με ελάχιστο εμβαδό που να έχουν σύνορο δοθείσα καμπύλη.

Η θεωρία των επιφανειών ελάχιστης έκτασης είχε μεγάλη ανάπτυξη κατά τον 19o αιώνα. Πολλά σημαντικά και δύσκολα αποτελέσματα έχουν αποδειχθεί τα τελευταία είκοσι χρόνια και εξακολουθούν να προκύπτουν, όπως για παράδειγμα ότι κάθε εμφυτευμένη, απλά συνεκτική επιφάνεια ελάχιστης έκτασης στον ℝ3 είναι είτε ένα επίπεδο είτε ένα ελικοειδές ([7]).

11.3 Ασκήσεις

1. ΄Εστω M μια ευθειογενής επιφάνεια με τοπική παραμέτρηση X : I × ℝ*→ ℝ3, X(t,s) = γ(t) + sυ(t), όπου γ : I → ℝ3 μια κανονική καμπύλη και υ : I → S2 μια λεία απεικόνιση. Η επιφάνεια M ονομάζεται αναπτυκτή (developable), εάν κάθε εφαπτόμενο επίπεδο κατά μήκος των σημείων ενός γεννήτορα παραμένει σταθερό. Αποδείξτε ότι η M είναι αναπτυκτή εάν και μόνο εάν ισχύει

det[˙γ v v′] ≡ 0.

2. ΄Εστω M ⊂ ℝ3 μια συμπαγής επιφάνεια με καμπυλότητα Gauss K σταθερά θετική. ΄Εστω ότι η απόλυτη τιμή |H| της μέσης καμπυλότητας είναι σταθερή. Αποδείξτε ότι η M είναι μια σφαίρα.

3. ΄Εστω M μια επιφάνεια με καμπυλότητα Gauss K ≡ 0 και έστω p ∈ M ένα παραβολικό σημείο. Αποδείξτε ότι η μοναδική ασυμπτωτική ευθεία, η οποία διέρχεται από το p, είναι ένα (ανοικτό) ευθύγραμμο τμήμα, το οποίο περιέχεται στην επιφάνεια M.

4. Αποδείξτε ότι οι επιφάνειες με τοπικές παραμετρήσεις

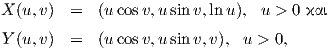
X (u,v) = (ucos v,usinv,lnu), u > 0 και Y (u,v) = (ucos v,usinv,v), u > 0,
έχουν την ίδια καμπυλότητα Gauss
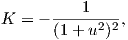
----1---- K = - (1+ u2)2 ,
αλλά δεν είναι ισομετρικές. Συνεπώς στο Θεώρημα Minding οι επιφάνειες είναι απαραίτητο να έχουν καμπυλότητες Gauss σταθερές (και όχι συναρτήσεις).

5. Θεωρούμε μια κανονική επιφάνεια με τοπική παραμέτρηση X(u,υ), με πρώτη θεμελιώδη μορφή Edu2 + 2Fdudυ + Gdυ2 και με απεικόνιση Gauss N. Αποδείξτε ότι τα εξής είναι ισοδύναμα:

΄Οταν ικανοποιείται μια από τις παραπάνω συνθήκες, τότε λέμε ότι οι παραμετρικές γραμμές της παραμέτρησης X αποτελούν ένα δίκτυο Chebyshev (Chebyshev net). Αποδείξτε στη συνέχεια ότι, η X επιδέχεται μια αναπαραμέτρηση 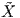˜ X(ũ,ṽ), της οποία η πρώτη θεμελιώδης μορφή είναι

2 2 du˜ + 2 cos θd˜ud˜v + d˜v ,
όπου θ μια διαφορίσιμη συνάρτηση του (ũ,ṽ). Δείξτε επίσης, ότι η γωνία θ είναι η γωνία των παραμετρικών γραμμών της ˜ X.

Βιβλιογραφία

[1]   M. Abate and F. Torena, Curves and Surfaces, Springer 2012.

[2]   M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall 1976.

[3]   P. Hartman and L. Nirenberg, On spherical images whose Jacobians do not change signs, Amer. J. Math., 81 (1959) 901–920.

[4]   D. Hilbert, Über Flächen von konstanter Gausscher Krümung, Trans. Amer. Math. Soc., 2 (1901) 97–99.

[5]   E. Holmgren, Sur les surfaces à courbure constante negative, C.R. Acad. Sci. Paris, 134 (1902) 740–743.

[6]   W.S. Massey, Surfaces of Gaussian curvature zero in Euclidean space, Tohoku Math. J., 14 (1963) 73–79.

[7]   W. Meeks III and H. Rosenberg, The uniqueness of the helicoid, Ann. Math., 161 (2005) 727–758.

[8]   Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, 2013.

[9]   A. Pressley, Elementary Differential Geometry, Second Edition, Springer 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.