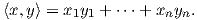
Σύνοψη
Μελετάμε ιδιότητες παραμετρημένων καμπυλών στο επίπεδο και στον χώρο. Το συνοδεύον τρίεδρο
του Frenet είναι μια ορθοκανονική βάση του ℝ3 προσαρτημένη σε κάθε σημείο μιας καμπύλης στον
χώρο, μέσω της οποίας πραγματοποιείται η μελέτη της. Η βασική αναλλοίωτη ποσότητα μιας επίπεδης
καμπύλης είναι η καμπυλότητά της. Μια καμπύλη στον χώρο έχει δύο αναλλοίωτες ποσότητες, την
καμπυλότητα και τη στρέψη της. Οι συναρτήσεις αυτές καθορίζουν πλήρως τη θέση μιας καμπύλης ως
προς μια στερεά κίνηση. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6],
[7].
Προαπαιτούμενη γνώση
Αναλυτική Γεωμετρία, Απειροστικός Λογισμός, Εισαγωγή στη Γραμμική ΄Αλγεβρα.
Θεωρούμε τον n-διάστατο πραγματικό χώρο ℝn = {(x1,…,xn) : xi ∈ ℝ} εφοδιασμένον με το συνηθισμένο Ευκλείδειο εσωτερικό γινόμενο ⟨⋅,⋅⟩ : ℝn × ℝn → ℝ0+
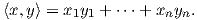
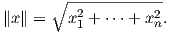
Για δύο συναρτήσεις γ,β : I → ℝn, ορίζουμε τη συνάρτηση: f : I → ℝn,f(t) = ⟨γ(t),β(t)⟩. Τότε προκύπτει εύκολα ο παρακάτω κανόνας παραγώγισης:
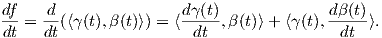
Ορισμός 1.1: Μια παραμετρημένη καμπύλη (parametrized curve) στον ℝn είναι μια διαφορίσιμη (λεία) απεικόνιση γ : I → ℝn, όπου I οποιοδήποτε ανοικτό διάστημα της πραγματικής ευθείας ℝ. Η εικόνα γ(I) ⊂ ℝn της απεικόνισης γ ονομάζεται ίχνος ή τροχιά της καμπύλης.
Παρατηρήσεις.
1. Πολλές φορές χρησιμοποιούμε τον όρο "καμπύλη" τόσο για την απεικόνιση γ : I → ℝn όσο και για το ίχνος
της.
2. Λέμε ότι η καμπύλη γ : I → ℝn αποτελεί μια παραμέτρηση (parametrization) του ίχνους γ(I).
3. Επειδή γ(t) ∈ ℝn, θα είναι γ(t) = (γ1(t),…,γn(t)), όπου γi : I → ℝ είναι διαφορίσιμες συναρτήσεις.
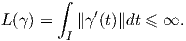
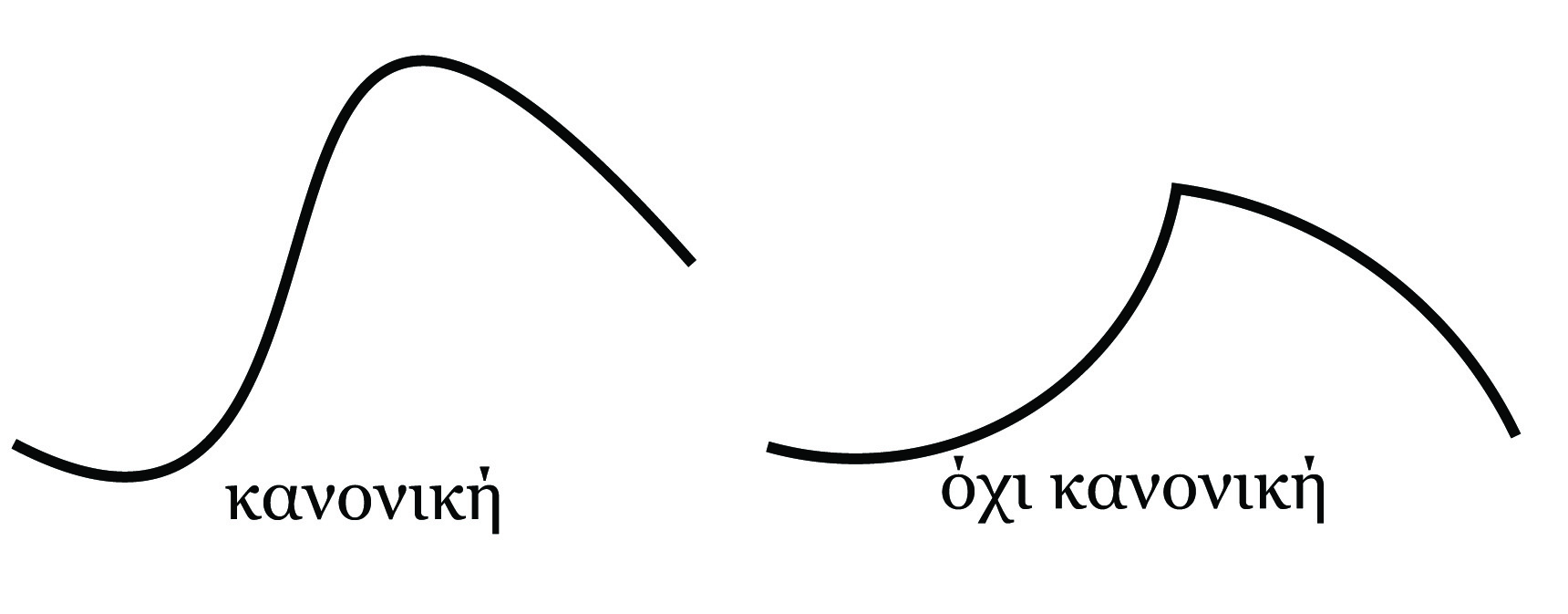
Από εδώ και στο εξής, όταν γράφουμε ῾῾καμπύλη᾿᾿, θα εννοούμε ῾῾κανονική καμπύλη᾿᾿.
Παραδείγματα.
1. ΄Εστω p≠q δύο σημεία του ℝ2. Η απεικόνιση γ : ℝ → ℝ2, γ(t) = (1 - t)p + tq αποτελεί μια παραμέτρηση της
ευθείας που διέρχεται απο τα σημεία p = γ(0) και q = γ(1).
2. Η εικόνα της καμπύλης γ : I → ℝ2 με γ′(t)≠0, για κάθε t ∈ I, περιέχεται σε κύκλο με κέντρο το (0,0) αν και μόνο αν το διάνυσμα γ(t) είναι κάθετο στο γ′(t) για κάθε t ∈ I.
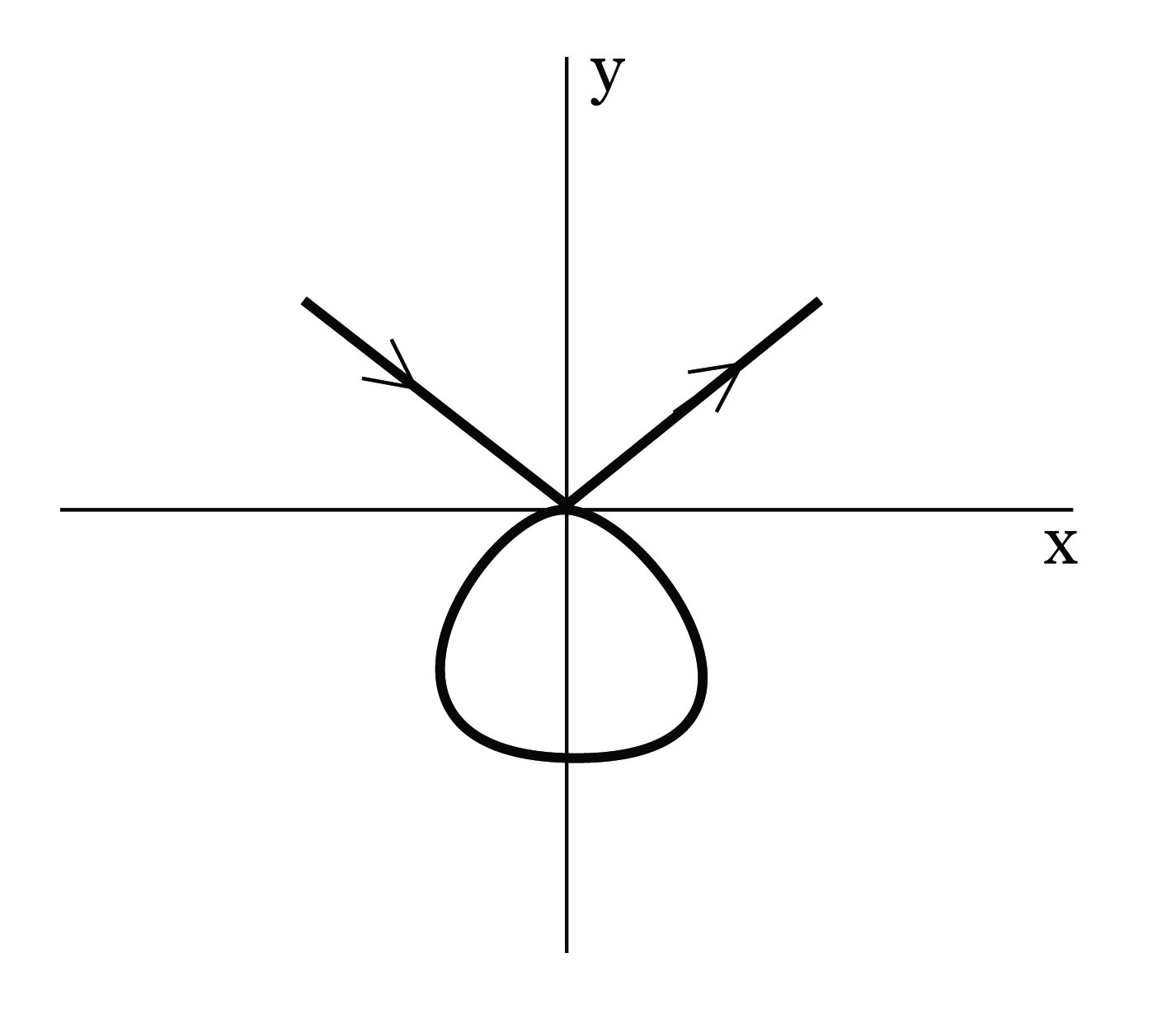
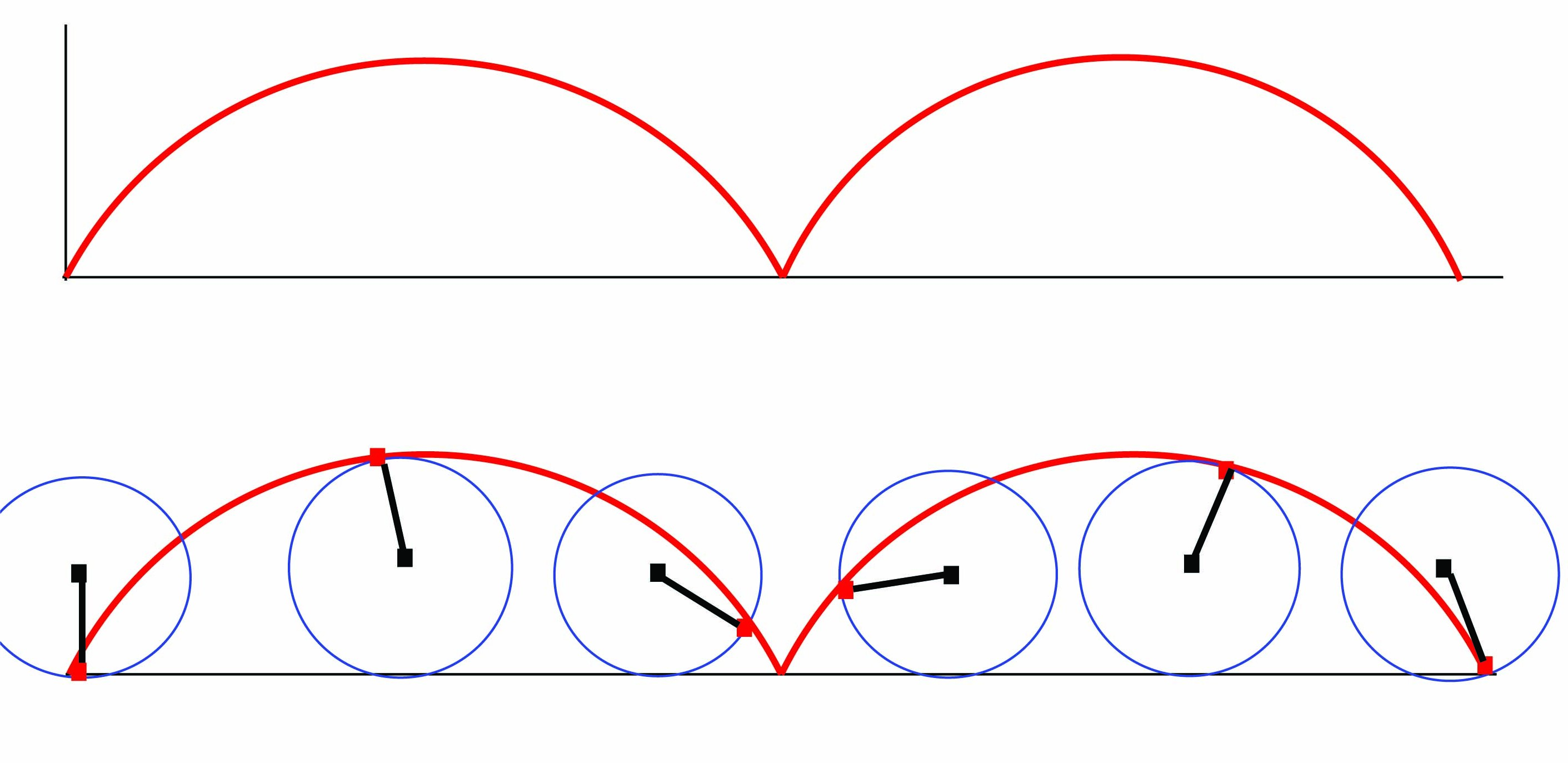
3. Η απεικόνιση γ : ℝ → ℝ2, γ(t) = (t,|t|) δεν είναι μια παραμετρημένη καμπύλη στο ℝ2. (Σχήμα 1.1)
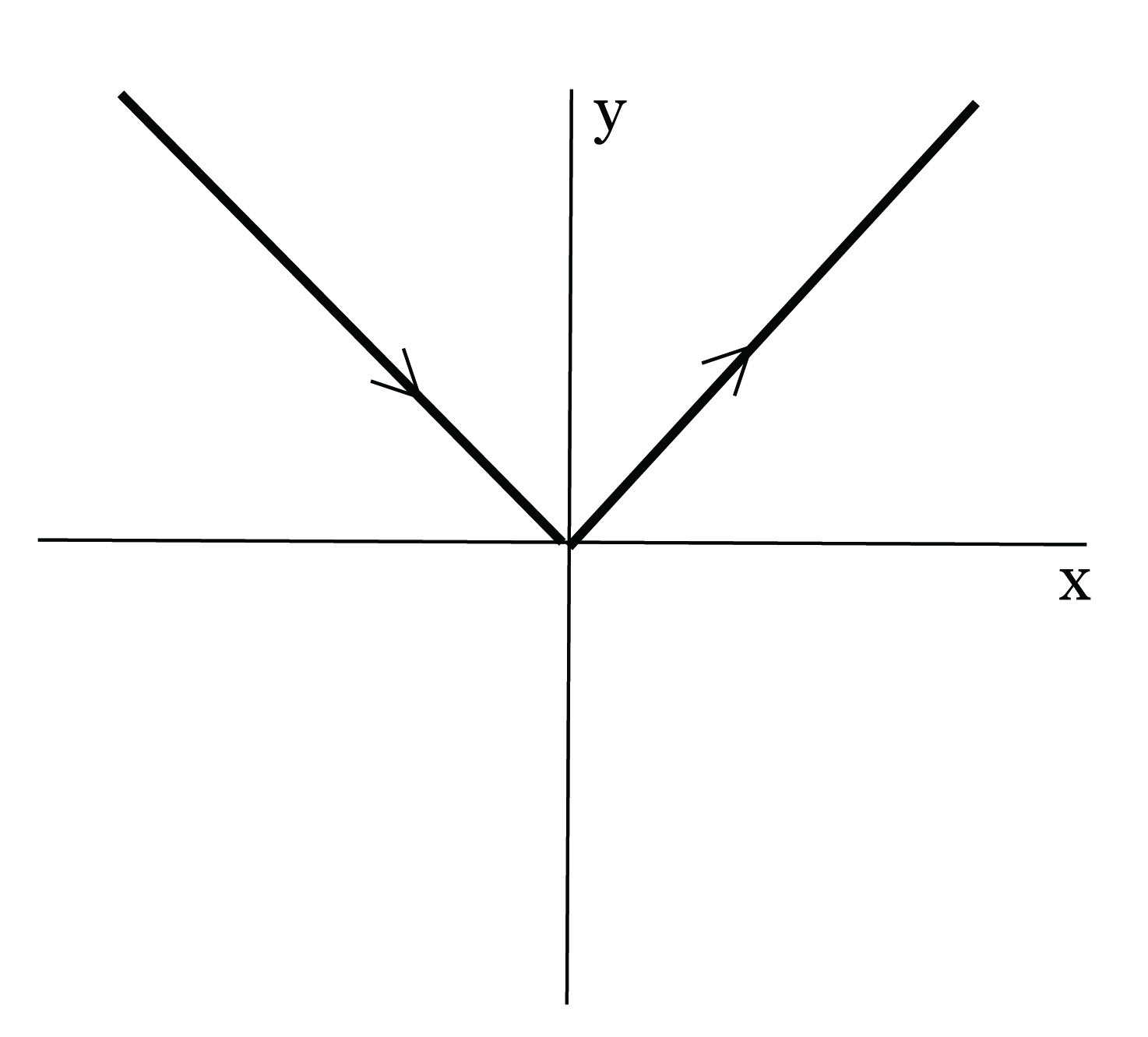
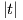 ).
).4. Η απεικόνιση γ : ℝ → ℝ2, γ(t) = (t3 - 4t,t2 - 4) ορίζει μια λεία καμπύλη στο επίπεδο. Η απεικόνιση αυτή δεν είναι 1-1 (γ(2) = γ(-2) = 0), αλλά αυτό δεν μας δημιουργεί πρόβλημα. (Σχήμα 1.2)
5. Η καμπύλη γ : ℝ → ℝ2, γ(t) = (t3,t2) δεν είναι κανονική, επειδή γ′(0) = (0,0).
6. ΄Εστω p ∈ ℝ2 και r > 0. Τότε η απεικόνιση γ : ℝ → ℝ2, γ(t) = p + r(cost,sint) αποτελεί μια παραμέτρηση του κύκλου με κέντρο το σημείο p και ακτίνα r. Το μήκος της γ στο διάστημα [0,2π) είναι
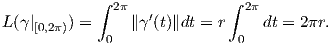
7. Οι απεικονίσεις γ1,γ2 : ℝ → ℝ2, γ1(t) = (cost,sint), γ2(t) = (cos(2t),sin(2t)), αποτελούν δύο παραμετρήσεις
του κύκλου με κέντρο (0,0) και ακτίνα 1, αλλά το διάνυσμα ταχύτητας της γ2 έχει διπλάσιο μέτρο από αυτό της
γ1.
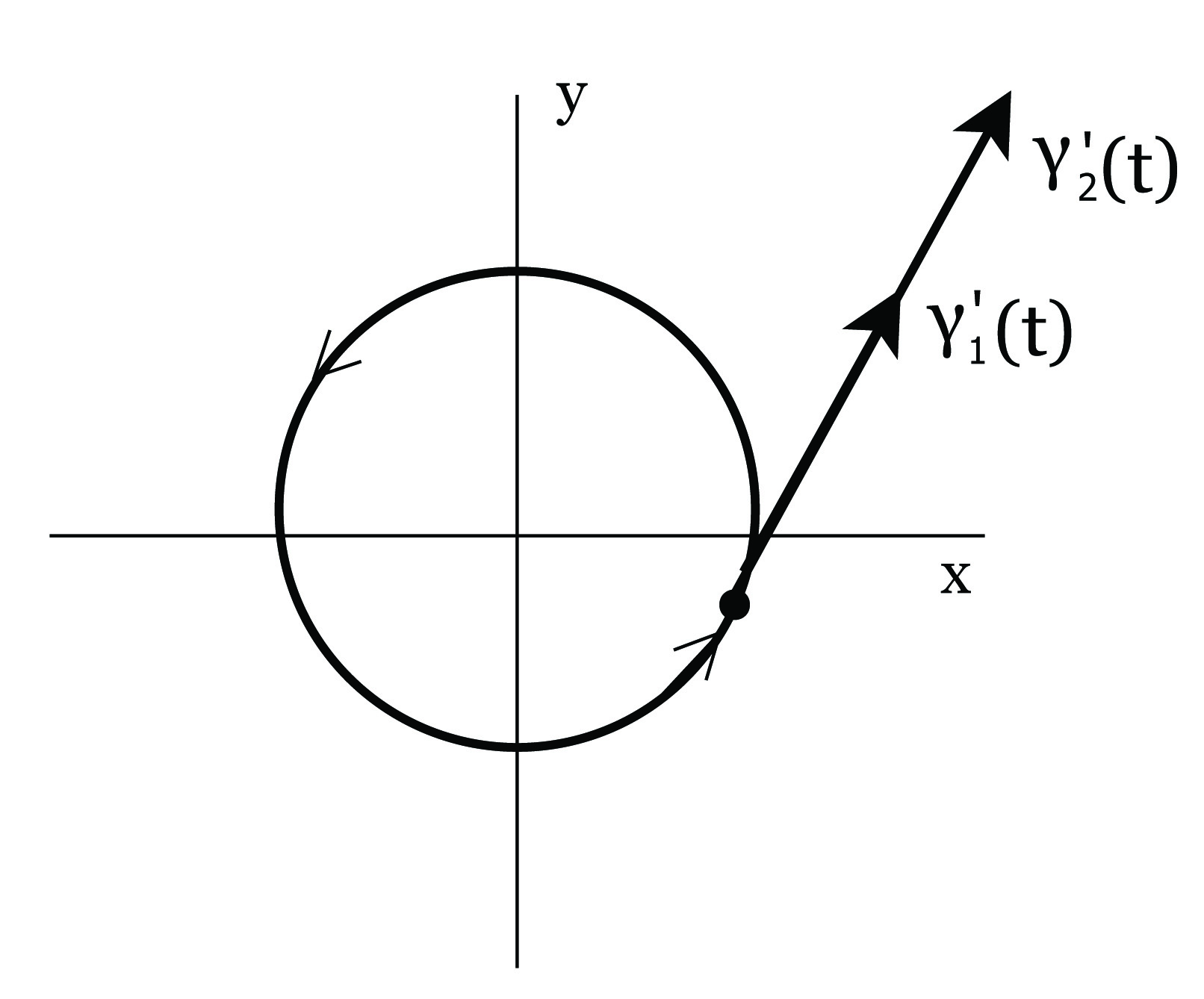
Λέγοντας εφαπτομένη μιας καμπύλης γ στο σημείο γ(t0) αυτής, εννοούμε την ευθεία που διέρχεται από το σημείο γ(t0) και είναι παράλληλη προς το διάνυσμα γ′(t0). Αυτή δίνεται από τη διανυσματική παραμετρική εξίσωση
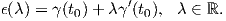 | (1.1) |
Είναι φανερό πως με λ = 0 έχουμε ϵ(0) = γ(t0). Ας υποθέσουμε τώρα ότι ϵ(λ) = (x1(λ),x2(λ),x3(λ)), γ(t0) = (x1(t0),x2(t0),x3(t0)) και γ′(t0) = (x1′(t0),x2′(t0),x3′(t0)). Τότε από την (1.1) προκύπτουν εύκολα οι ακόλουθες παραμετρικές εξισώσεις της εφαπτομένης:
Αν τώρα μεταξύ των (1.2) απαλείψουμε την παράμετρο λ, τότε προκύπτουν οι χωρίς παράμετρο εξισώσεις της εφαπτομένης της καμπύλης. Πράγματι, έχουμε εύκολα: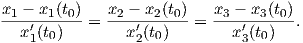
Παράδειγμα 1.1: Θα προσδιορίσουμε την εφαπτόμενη της κυκλικής έλικας
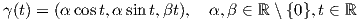
Είναι γ′(t) = (-α sint,α cost,β), οπότε γ′(π∕4) = (-α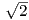 ∕2,,α
∕2,,α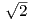 ∕2,β). Αλλά είναι και γ(π∕4) =
(α
∕2,β). Αλλά είναι και γ(π∕4) =
(α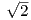 ∕2,α
∕2,α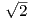 ∕2,βπ∕4). Η εξίσωση λοιπόν (1.1) της εφαπτομένης της καμπύλης γίνεται:
∕2,βπ∕4). Η εξίσωση λοιπόν (1.1) της εφαπτομένης της καμπύλης γίνεται:
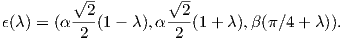
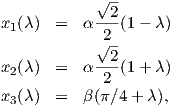
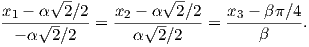
Ορισμός 1.3: ΄Εστω γ : I → ℝn και 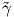 : J → ℝn δύο λείες καμπύλες. Θα λέμε ότι η καμπύλη
: J → ℝn δύο λείες καμπύλες. Θα λέμε ότι η καμπύλη 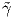 αποτελεί
μια αναπαραμέτρηση (reparametrization) της γ, εάν υπάρχει μια αμφιδιαφόριση h : J → I, τέτοια ώστε
αποτελεί
μια αναπαραμέτρηση (reparametrization) της γ, εάν υπάρχει μια αμφιδιαφόριση h : J → I, τέτοια ώστε
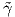 = γ ∘ h.
= γ ∘ h.
Στον παραπάνω ορισμό η έκφραση ῾῾ η h είναι αμφιδιαφόριση᾿᾿ σημαίνει ότι η απεικόνιση h είναι διαφορίσιμη, 1-1, επί, καθώς και η αντίστροφή της είναι διαφορίσιμη.
Είναι προφανές ότι κάθε αναπαραμέτρηση μιας καμπύλης γ έχει την ίδια εικόνα με αυτήν. ΄Ετσι στο Παράδειγμα 7 η καμπύλη γ2 αποτελεί μια αναπαραμέτρηση της γ1, διότι γ2(t) = (γ1 ∘ h)(t), όπου h : ℝ → ℝ είναι η αμφιδιαφόριση με τιμή h(t) = 2t. Επίσης, αν η καμπύλη γ είναι κανονική τότε και η αναπαραμέτρησή της θα είναι κανονική. Στη συνέχεια, θα αποδείξουμε ότι το μήκος τόξου μιας καμπύλης είναι ανεξάρτητο από την αναπαραμέτρηση αυτής.
Απόδειξη. ΄Εστω γ : [a,b] → ℝ3 και 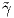 : [a′,b′] → ℝ3 μια αναπαραμέτρηση της γ με
: [a′,b′] → ℝ3 μια αναπαραμέτρηση της γ με 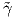 = γ ∘ h, όπου
h : [a′,b′] → [a,b] μια αμφιδιαφόριση. ΄Εχουμε
= γ ∘ h, όπου
h : [a′,b′] → [a,b] μια αμφιδιαφόριση. ΄Εχουμε
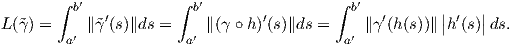
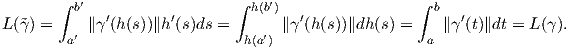
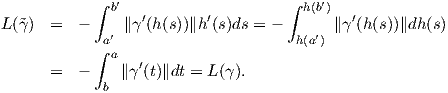
΄Εστω γ : I → ℝn μια κανονική καμπύλη, t0 ∈ I. Για δοθέν t ∈ I θεωρούμε το μήκος τόξου
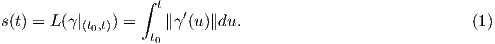
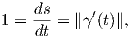
Ορισμός 1.4: Μια λεία καμπύλη γ : I → ℝn έχει παραμέτρηση ως προς το μήκος τόξου εάν ∥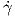 (s)∥ = 1,
για κάθε s ∈ I.
(s)∥ = 1,
για κάθε s ∈ I.
Παρατηρήσεις.
1. ΄Οταν η γ έχει παραμέτρηση ως προς το μήκος τόξου, θα γράφουμε 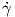 (s) αντί γ′(s). Στην περίπτωση αυτή θα
συμβολίζουμε την παράμετρο της γ με s αντί με t.
(s) αντί γ′(s). Στην περίπτωση αυτή θα
συμβολίζουμε την παράμετρο της γ με s αντί με t.
2. Το μέτρο ∥γ′(t)∥ ονομάζεται ταχύτητα της γ, οπότε μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου έχει μοναδιαία ταχύτητα.
3. Αν Sn-1 = {(x1,…,xn) ∈ ℝn : x12 +  + xn2 = 1} είναι η μοναδιαία σφαίρα στον ℝn, τότε για μια καμπύλη γ
αυτής με παραμέτρηση ως προς το μήκος τόξου οι εφαπτόμενες
+ xn2 = 1} είναι η μοναδιαία σφαίρα στον ℝn, τότε για μια καμπύλη γ
αυτής με παραμέτρηση ως προς το μήκος τόξου οι εφαπτόμενες 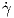 (s) είναι στοιχεία της Sn-1 (αντί απλώς του
ℝn).
(s) είναι στοιχεία της Sn-1 (αντί απλώς του
ℝn).
Ισχύει η εξής πρόταση από τη διανυσματική ανάλυση:
Πρόταση 1.2: ΄Εστω f : I → ℝn μια διανυσματική συνάρτηση τέτοια ώστε ∥f(t)∥ = c, σταθερό. Τότε ισχύει ⟨f′(t),f(t)⟩ = 0, δηλαδή είτε f′(t) = 0 είτε το διάνυσμα f′(t) είναι κάθετο στο f(t) για κάθε t ∈ I.
Απόδειξη. Επειδή ∥f(t)∥ = c προκύπτει ότι f(t)≠0, επίσης έχουμε:

Συμπέρασμα. Αν μια καμπύλη γ : I → ℝn έχει παραμέτρηση ως προς το μήκος τόξου, τότε είτε 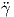 (s) = 0 είτε το
διάνυσμα
(s) = 0 είτε το
διάνυσμα 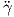 (s) είναι κάθετο στο
(s) είναι κάθετο στο 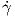 (s).
(s).
Το ενδιαφέρον είναι ότι κάθε κανονική καμπύλη επιδέχεται μια παραμέτρηση ως προς το μήκος τόξου.
Θεώρημα 1.1: ΄Εστω γ : (α,β) → ℝn μια κανονική καμπύλη του ℝn. Τότε το ίχνος γ((α,β)) της γ είναι δυνατόν να παραμετροποιηθεί ως προς το μήκος τόξου.
Απόδειξη. Ορίζουμε τη συνάρτηση μήκους τόξου σ : (a,b) → ℝ+, σ(t) = ∫ at∥γ′(u)∥du. Τότε σ′(t) = ∥γ′(t)∥ > 0, δηλαδή η συνάρτηση σ είναι γνησίως αύξουσα και σ((a,b)) = (0,L(γ)). ΄Εστω τ : (0,L(γ)) → (a,b) η αντίστροφη συνάρτηση της σ, δηλαδή σ(τ(s)) = s για κάθε s ∈ (0,L(γ)). Παραγωγίζοντας την προηγούμενη σχέση, παίρνουμε:
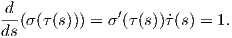
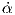 (s) = γ′(τ(s))
(s) = γ′(τ(s))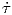 (s), επομένως
(s), επομένως 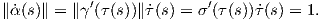
Συμβολίζουμε με Mn×n(ℝ) το σύνολο όλων των πραγματικών n × n πινάκων.
Ορισμός 1.5: Μια απεικόνιση Φ : ℝn → ℝn ονομάζεται Ευκλείδεια (ή στερεά) κίνηση (rigit motion) εάν έχει τη μορφή
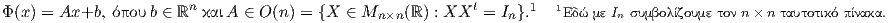
Μια Ευκλείδεια κίνηση Φ διατηρεί τον προσανατολισμό εάν
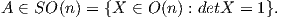
΄Ασκηση. Γράψτε αναλυτικά τα στοιχεία των ομάδων O(2) και SO(2).
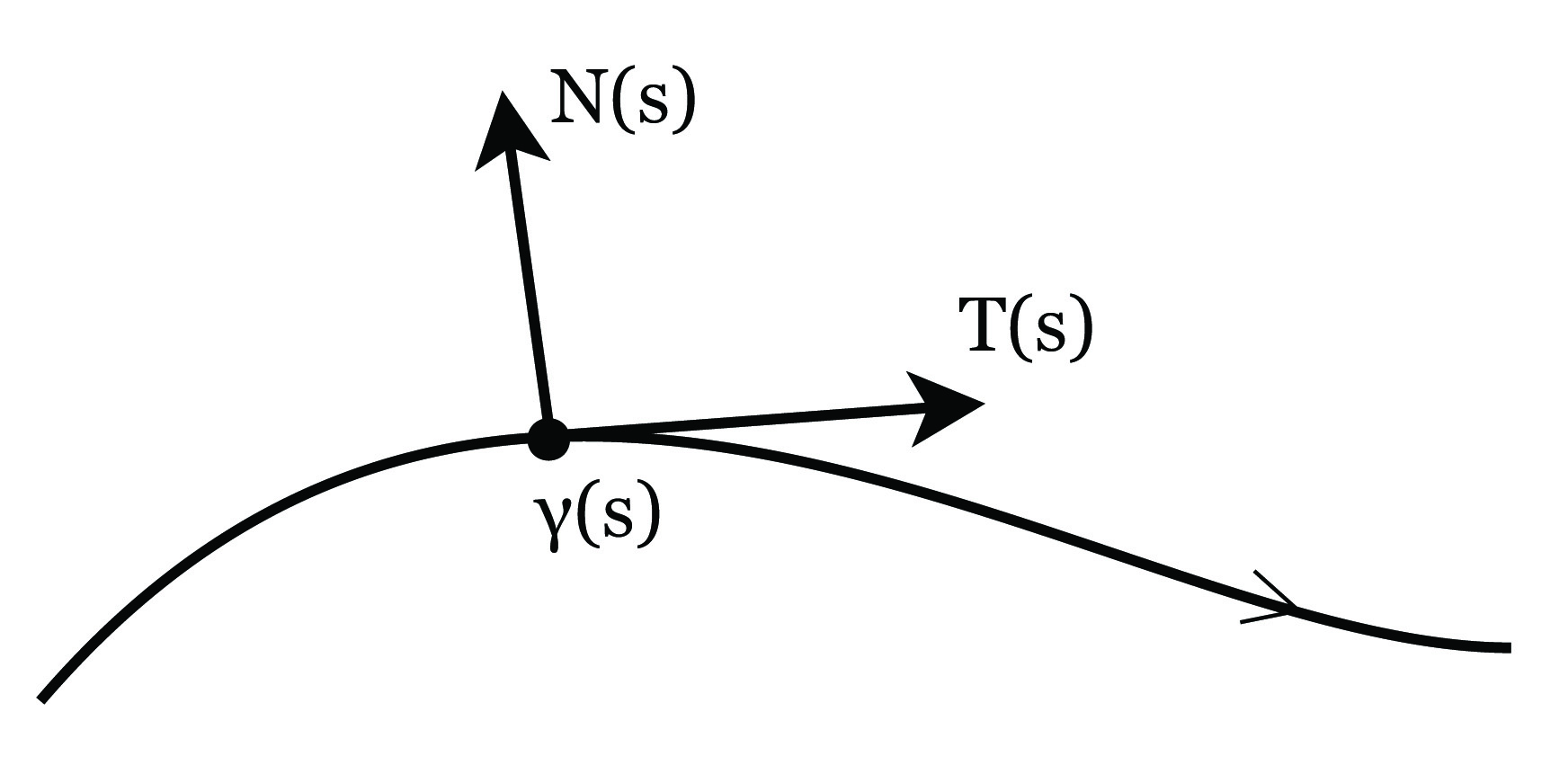
Περιοριζόμαστε τώρα σε καμπύλες του επιπέδου ℝ2. ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη me param�trhsh wc proc to m�koc t�xou. Ορίζουμε το εφαπτόμενο διάνυσμα κατά μήκος της γ ως
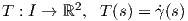
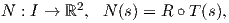
 που δίνεται ως
που δίνεται ως
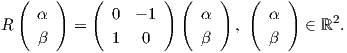
Θα ορίσουμε τώρα ένα σημαντικό μέτρο της κύρτωσης μιας επίπεδης καμπύλης.
Ορισμός 1.6: ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Καμπυλότητα (curvature) της γ λέγεται η συνάρτηση κ : I → ℝ0+, με τιμή
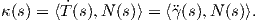
Παρατηρήσεις.
1. Η καμπυλότητα, όπως ορίστηκε παραπάνω, αποτελεί ένα μέτρο του πόσο γρήγορα το μοναδιαίο εφαπτόμενο
διάνυσμα T(s) = 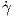 (s) στρέφεται προς τη διεύθυνση του κάθετου διανύσματος N(s) ή ισοδύναμα απομακρύνεται
από τον φορέα του T(s).
(s) στρέφεται προς τη διεύθυνση του κάθετου διανύσματος N(s) ή ισοδύναμα απομακρύνεται
από τον φορέα του T(s).
2. Για κ(s)≠0 η ακτίνα καμπυλότητας της γ στο σημείο γ(s) ορίζεται ως
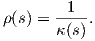
Θεώρημα 1.2: ΄Εστω γ : I → ℝ2 καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε το πλαίσιο Frenet ικανοποιεί το παρακάτω σύστημα συνήθων διαφορικών εξισώσεων.
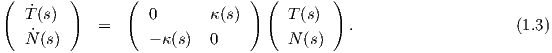
Απόδειξη. Η καμπύλη γ έχει παράμετρο το μήκος τόξου της, οπότε τα διανύσματα T(s) και N(s) ορίζουν μια ορθοκανονική βάση του ℝ2. Συνεπώς ⟨T(s),N(s)⟩ = 0, επομένως θα έχουμε
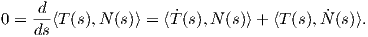
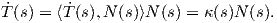
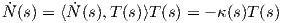
Θεώρημα 1.3: ΄Εστω γ : I → ℝ2 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε η καμπυλότητα κ : I → ℝ είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(I) της καμπύλης είναι τμήμα ευθείας (ή και ολόκληρη ευθεία).
Απόδειξη. ΄Εστω κ(s) = 0 για κάθε s, δηλαδή ⟨Ṫ(s),N(s)⟩ = 0. Τότε, επειδή N(s)≠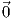 , θα έχουμε ότι Ṫ(s) =
, θα έχουμε ότι Ṫ(s) = 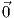 για
κάθε s ∈ I. Ολοκληρώνοντας παίρνουμε T(s) = c1 ή γ′(s) = c1, όπου το c1 είναι ένα τυχαίο διάνυσμα του ℝ2. Αν
ολοκληρώσουμε την τελευταία εξίσωση θα έχουμε
για
κάθε s ∈ I. Ολοκληρώνοντας παίρνουμε T(s) = c1 ή γ′(s) = c1, όπου το c1 είναι ένα τυχαίο διάνυσμα του ℝ2. Αν
ολοκληρώσουμε την τελευταία εξίσωση θα έχουμε
Κάθε επίπεδη καμπύλη καθορίζεται πλήρως (μη λαμβάνοντας υπόψη προσανατολισμένες στερεές κινήσεις του επιπέδου) από την καμπυλότητά της, όπως αναφέρεται στο παρακάτω θεώρημα.
Θεώρημα 1.4: ΄Εστω κ : I → ℝ μια διαφορίσιμη απεικόνιση. Τότε υπάρχει μια κανονική καμπύλη γ : I → ℝ2
με παραμέτρηση κατά μήκος τόξου, η οποία να έχει καμπυλότητα κ. Επιπλέον, εάν 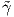 : I → ℝ2 είναι μια
άλλη τέτοια καμπύλη, τότε υπάρχει πίνακας A ∈ SO(2) και διάνυσμα b ∈ ℝ2 τέτοια ώστε
: I → ℝ2 είναι μια
άλλη τέτοια καμπύλη, τότε υπάρχει πίνακας A ∈ SO(2) και διάνυσμα b ∈ ℝ2 τέτοια ώστε
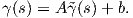
Στη διαφορική γεωμετρία το ενδιαφέρον μας εστιάζεται σε εκείνες τις ιδιότητες γεωμετρικών αντικειμένων, οι οποίες δεν εξαρτώνται από την παραμέτρηση. Συνεπώς, η καμπυλότητα μιας καμπύλης δεν θα πρέπει να εξαρτάται από την επιλογή της παραμέτρησης.
Ορισμός 1.7: ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη (όχι απαραίτητα με παραμέτρηση κατά μήκος τόξου).
΄Εστω 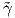 = γ ∘ h : J → ℝ2 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια αμφιδιαφόριση
h : J → I και έστω
= γ ∘ h : J → ℝ2 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια αμφιδιαφόριση
h : J → I και έστω 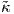 : J → ℝ η καμπυλότητα της
: J → ℝ η καμπυλότητα της 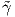 . Για κάθε t ∈ I η καμπυλότητα της καμπύλης γ στο
σημείο t είναι ο αριθμός
. Για κάθε t ∈ I η καμπυλότητα της καμπύλης γ στο
σημείο t είναι ο αριθμός
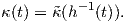
Απόδειξη. ΄Εστω  = γ ∘ h : J → ℝ2 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s-1
και s η συνάρτηση μήκους τόξου. ΄Εστω
= γ ∘ h : J → ℝ2 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s-1
και s η συνάρτηση μήκους τόξου. ΄Εστω 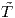 , Ñ το πλαίσιο Frenet κατά μήκος της καμπύλης
, Ñ το πλαίσιο Frenet κατά μήκος της καμπύλης 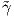 και
και
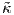 η καμπυλότητα αυτής. Τότε γ =
η καμπυλότητα αυτής. Τότε γ = 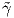 ∘ h-1 ή ισοδύναμα γ =
∘ h-1 ή ισοδύναμα γ = 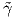 ∘ s, οπότε για κάθε t ∈ I, έχουμε:
∘ s, οπότε για κάθε t ∈ I, έχουμε:
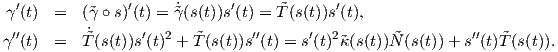
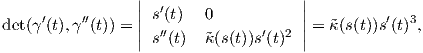
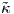 (s(t)) =
(s(t)) = 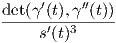 . ΄Ομως s(t) = ∫
t0t∥γ′(u)∥du οπότε s′(t) = ∥γ′(t)∥. ΄Αρα
. ΄Ομως s(t) = ∫
t0t∥γ′(u)∥du οπότε s′(t) = ∥γ′(t)∥. ΄Αρα
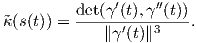
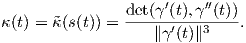
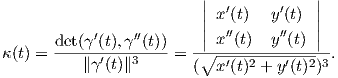
Πόρισμα 1.1: ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη. Τότε το ίχνος γ(I) της γ είναι τμήμα ευθείας εάν και μόνο εάν τα διανύσματα γ′(t) και γ′′(t) είναι γραμμικώς εξαρτημένα για κάθε t ∈ I.
Μια ενδιαφέρουσα εφαρμογή της θεωρίας των επίπεδων καμπυλών αποτελεί η ισοπεριμετρική ανισότητα. Η ανισότητα αυτή απαντά στο εξής απλό πρόβλημα, το οποίο είχε διατυπωθεί στην αρχαιότητα και η λύση του ήταν γνωστή στους αρχαίους ΄Ελληνες: ῾῾ποιό είναι το σχήμα που πρέπει να λάβει ένα κλειστό σχοινί στο επίπεδο, ώστε το εμβαδό που περικλείει να είναι το μέγιστο δυνατό;᾿᾿. Η πρώτη αυστηρή απόδειξη της ισοπεριμετρικής ανισότητας δόθηκε τον 19ο αιώνα. Αυτή έχει πολλές σύγχρονες διατυπώσεις και εξακολουθεί να ελκύει το ενδιαφέρον των μαθηματικών από διάφορες σκοπιές. Προκειμένου να τη διατυπώσουμε, χρειαζόμαστε τα εξής εισαγωγικά.
Ορισμός 1.8: Μια συνεχής απεικόνιση γ : ℝ → ℝ2 αποτελεί παραμέτρηση μιας απλής κλειστής καμπύλης, εάν η γ είναι περιοδική με περίοδο L > 0 και ο περιορισμός γ|[0,L) : ℝ → ℝ2 είναι απεικόνιση 1-1. (Ισοδύναμα γ(t) = γ(t′) εάν και μόνο εάν t′- t = kL για k ∈ ℤ).

Το παρακάτω θεώρημα είναι απλό στη διατύπωσή του, αλλά δύσκολο στην απόδειξη.
Θεώρημα 1.5: (Κλειστής καμπύλης του Jordan)
΄Εστω ότι η συνεχής απεικόνιση γ : ℝ → ℝ2 αποτελεί παραμέτρηση μιας απλής, κλειστής καμπύλης. Τότε
το υποσύνολο ℝ2 \ γ(ℝ) του επιπέδου αποτελείται ακριβώς από δύο συνεκτικές συνιστώσες.
Η μια συνιστώσα είναι φραγμένη και ονομάζεται εσωτερικό Int(γ) της γ και η άλλη δεν είναι φραγμένη και ονομάζεται εξωτερικό Ext(γ) της γ.
Ορισμός 1.9: Μια συνεχής απεικόνιση γ : ℝ → ℝ2 η οποία αποτελεί παραμέτρηση μιας απλής κλειστής καμπύλης έχει θετικό προσανατολισμό, εάν το κάθετο διάνυσμα
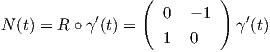
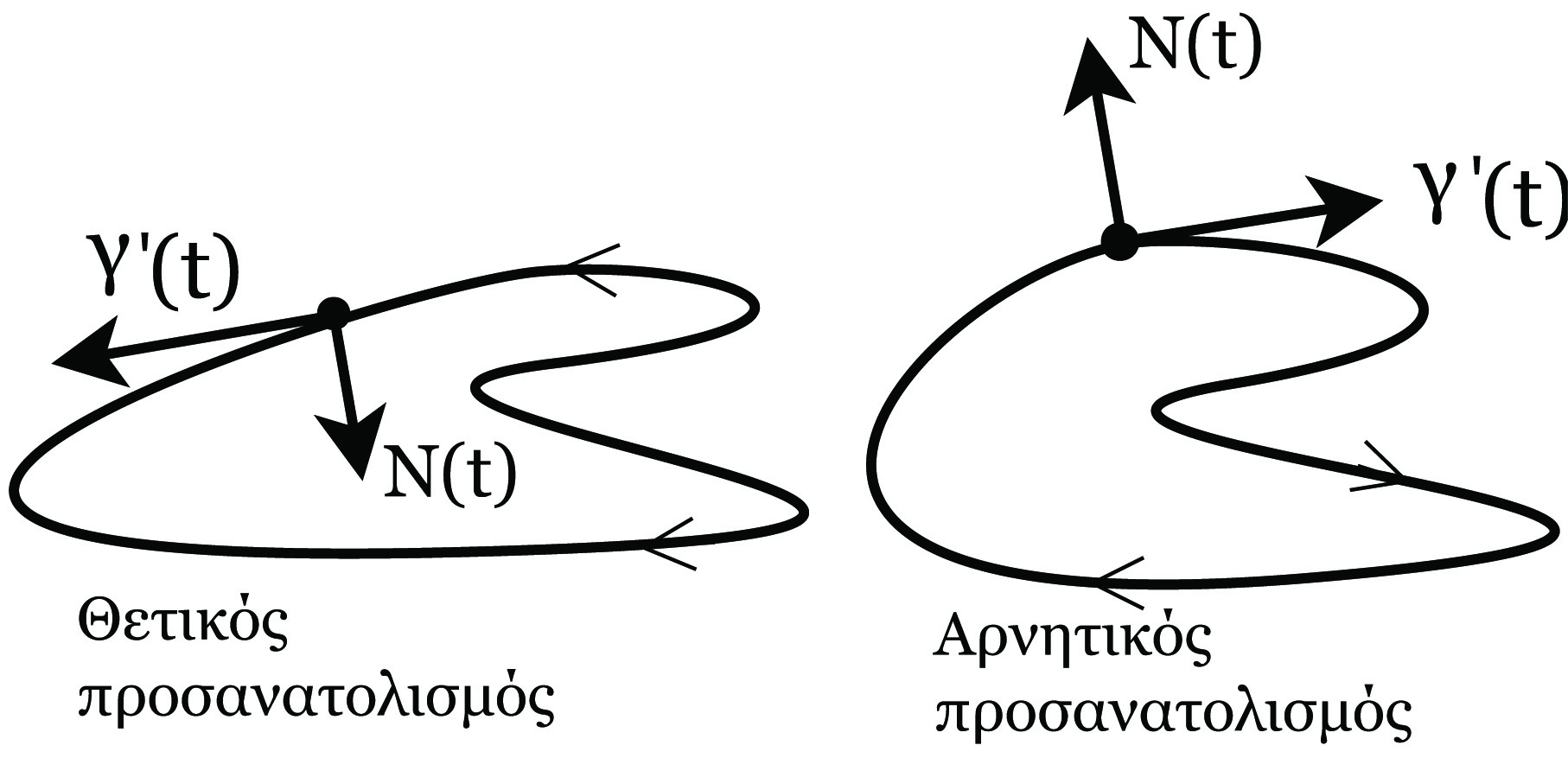
Θα χρειαστούμε το παρακάτω λήμμα, η απόδειξη του οποίου προκύπτει ως εφαρμογή του θεωρήματος Green από τη διανυσματική ανάλυση.
Λήμμα 1.1: ΄Εστω γ : ℝ → ℝ2 μια κανονική θετικά προσανατολισμένη απεικόνιση η οποία παραμετρικοποιεί μια επίπεδη, απλή κλειστή καμπύλη. Αν A είναι το εμβαδόν του εσωτερικού Int(γ) της γ, τότε
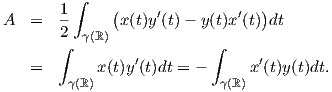
Θεώρημα 1.6: (Ισοπεριμετρική Ανισότητα)
΄Εστω C μια κανονική, απλή και κλειστή καμπύλη του επιπέδου με μήκος L. ΄Εστω A το εμβαδό της περιοχής
που περικλείεται από τη C. Τότε ισχύει η σχέση
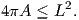
Απόδειξη. ΄Εστω l1 και l2 δύο παράλληλες ευθείες οι οποίες εφάπτονται στην καμπύλη C, με τρόπο τέτοιο ώστε η C να βρίσκεται εντός τις λωρίδας που σχηματίζουν οι δύο ευθείες (βλ. Σχήμα 1.8).
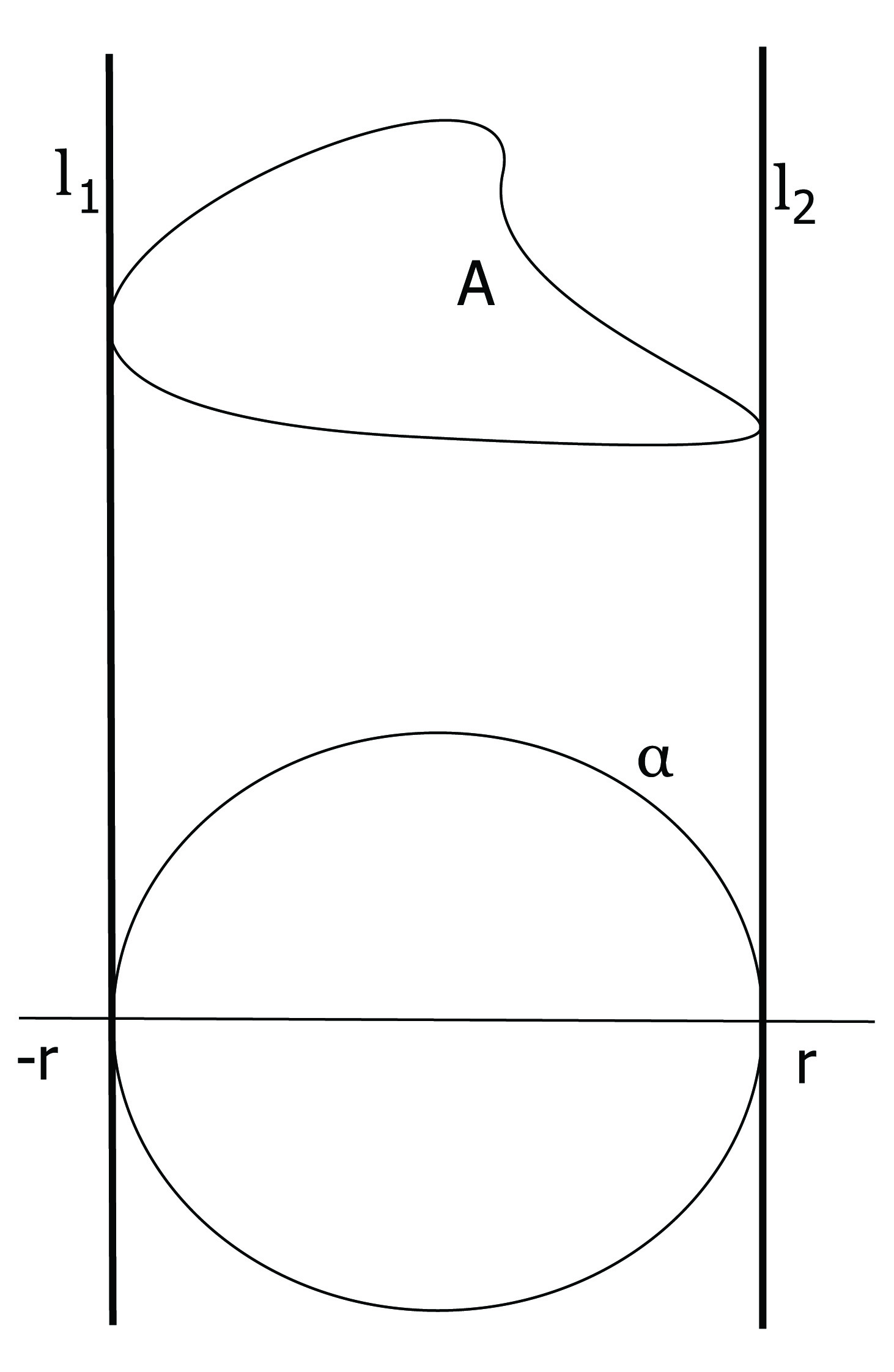
Εισάγουμε ένα σύστημα συντεταγμένων στο επίπεδο τέτοιο ώστε οι l1 και l2 να είναι κάθετες στον άξονα των x και άρα να περιγράφονται ως εξής:
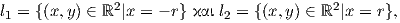
Ορίζουμε την καμπύλη α : ℝ → ℝ2 με τύπο α(s) = (x(s),ỹ(s)), όπου
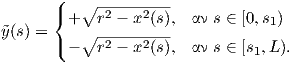
Ως άμεση συνέπεια του Λήμματος 1.1 έχουμε ότι
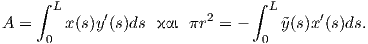
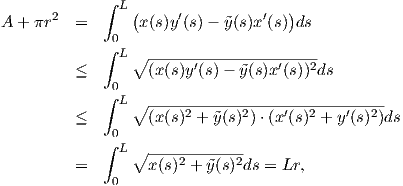
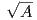 - r
- r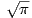 )2
= A - 2r
)2
= A - 2r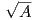
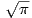 + πr2
προκύπτει ότι
+ πr2
προκύπτει ότι
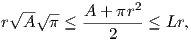

Θα μελετήσουμε τώρα καμπύλες γ : I → ℝ3 στον τρισδιάστατο χώρο ℝ3. Θα ορίσουμε την καμπυλότητα και τη στρέψη τέτοιων καμπυλών και θα δείξουμε ότι οι ποσότητες αυτές καθορίζουν τις καμπύλες αυτές ως προς τις στερεές κινήσεις του χώρου στον οποίο διατηρούν τον προσανατολισμό.
Θυμίζουμε το εξωτερικό και το μικτό γινόμενο στον χώρο ℝ3
Ορισμός 1.10: ΄Εστω u = (x1,y1,z1),υ = (x2,y2,z2) δύο διανύσματα του ℝ3. Το εξωτερικό γινόμενο του u με το υ είναι το διάνυσμα u×υ ∈ ℝ3 το οποίο είναι κάθετο στο επίπεδο που ορίζουν τα διανύσματα u και υ και δίνεται ως εξής:
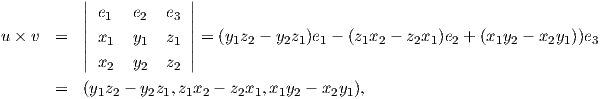
Το μέτρο του εξωτερικού γινομένου δύο μη μηδενικών διανυσμάτων u,υ είναι ίσο με το εμβαδόν του παραλληλογράμμου που ορίζεται από τα διανύσματα αυτά.
Από τον ορισμό του εξωτερικού γινομένου, προκύπτουν εύκολα οι ακόλουθες ιδιότητες. Για κάθε u,υ,z ∈ ℝ3 έχουμε
΄Εστω f,g : I ⊂ ℝ → ℝ3 δύο λείες καμπύλες. Τότε η απεικόνιση f × g : I ⊂ ℝ → ℝ3, t (f × g)(t) = f(t) × g(t)
είναι λεία και ισχύει ο παρακάτω κανόνας παραγώγισης
(f × g)(t) = f(t) × g(t)
είναι λεία και ισχύει ο παρακάτω κανόνας παραγώγισης
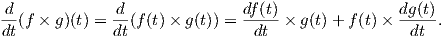
Ορισμός 1.11: ΄Εστω τρία διανύσματα u,υ,z του χώρου ℝ3. Ο πραγματικός αριθμός ⟨(u×υ),z⟩ ονομάζεται μικτό γινόμενο των διανυσμάτων u,υ,z και συμβολίζεται με [uυz], δηλαδή
![⟨(u × v),z⟩ = [uvz].](02_chapter_0193x.png)
Η απόλυτη τιμή του μικτού γινομένου τριών μη συνεπίπεδων διανυσμάτων είναι ίση με τον όγκο του παραλληλεπιπέδου, που ορίζεται από τα τρία διανύσματα.
Από τον ορισμό του μικτού γινομένου προκύπτουν εύκολα οι παρακάτω ιδιότητες. Για κάθε u,υ,z ∈ ℝ3:
Αρχίζουμε με μερικά παραδείγματα καμπυλών στον Ευκλείδειο χώρο ℝ3.
Παραδείγματα
1. ΄Εστω p≠q δύο σημεία στον ℝ3. Τότε η απεικόνιση γ : ℝ → ℝ3, με τιμή γ(t) = (1 - t)p + tq είναι μια
παραμέτρηση της ευθείας που διέρχεται από τα σημεία p = γ(0) και q = γ(1).
2. ΄Εστω {Z,W} μια ορθοκανονική βάση ενός επιπέδου V του ℝ3, r > 0 και p ∈ V ⊂ ℝ3. Τότε η απεικόνιση
γ : ℝ → ℝ3, γ(t) = p + r (cost)Z + (sint)W
(cost)Z + (sint)W αποτελεί μια παραμέτρηση του κύκλου ο οποίος βρίσκεται στο
(υπερ)επίπεδο p + V και έχει κέντρο το p και ακτίνα r.
αποτελεί μια παραμέτρηση του κύκλου ο οποίος βρίσκεται στο
(υπερ)επίπεδο p + V και έχει κέντρο το p και ακτίνα r.
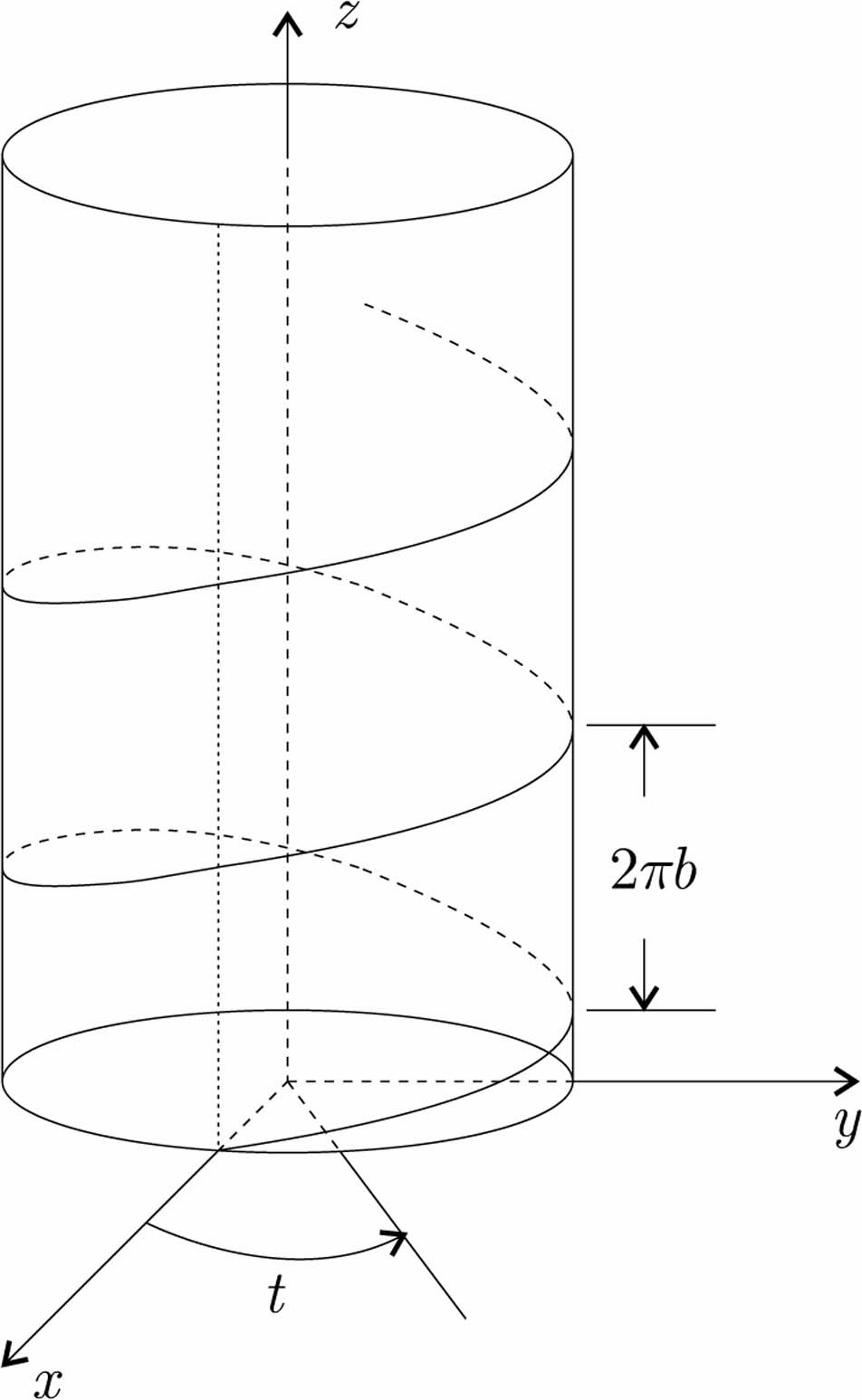
3. ΄Εστω r,a,b > 0. Η απεικόνιση
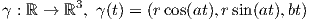
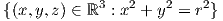
΄Εστω γ : I → ℝ3 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Καμπυλότητα της γ λέγεται η συνάρτηση κ : I → ℝ0+ με τιμή
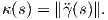
Θεώρημα 1.7: ΄Εστω γ : I → ℝ3 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε η καμπυλότητα κ : I → ℝ0+ της γ είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(I) της καμπύλης είναι τμήμα ευθείας (ή ολόκληρη ευθεία).
Απόδειξη. (Σκιαγράφηση)
Η καμπυλότητα κ(s) = ∥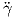 (s)∥ είναι ταυτοτικά μηδέν εάν και μόνο εάν υπάρχει μοναδιαίο διάνυσμα Z ∈ S2
και σημείο p ∈ ℝ3 τέτοια ώστε
(s)∥ είναι ταυτοτικά μηδέν εάν και μόνο εάν υπάρχει μοναδιαίο διάνυσμα Z ∈ S2
και σημείο p ∈ ℝ3 τέτοια ώστε
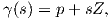
Ορισμός 1.13: Μια καμπύλη γ : I → ℝ3 με παραμέτρηση ως προς το μήκος τόξου ονομάζεται καμπύλη Frenet (καμιά φορά και ομαλή ή κανονική) εάν η καμπυλότητα κ είναι παντού μη μηδενική, δηλαδή κ(s)≠0 για κάθε s ∈ I.
΄Εστω γ : I → ℝ3 μια καμπύλη Frenet. Ορίζουμε τις παρακάτω σημαντικές διανυσματικές συναρτήσεις.
Το εφαπτόμενο διάνυσμα (tangent vector) κατά μήκος της γ
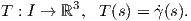
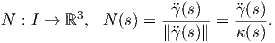
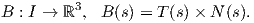
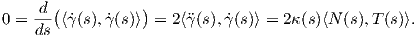
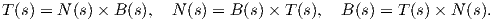
Στη συνέχεια θα ορίσουμε ένα άλλο βασικό, για τη μελέτη μιας καμπύλης μέγεθος.
Ορισμός 1.14: ΄Εστω γ : I → ℝ3 μια καμπύλη Frenet. Ορίζουμε τη στρέψη (torsion) της γ ως τη συνάρτηση
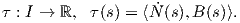
Παρατήρηση.
Η στρέψη αποτελεί ένα μέτρο του κάτα πόσο γρήγορα η πρώτη κάθετος N(s) = 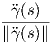 στρέφεται προς την
διεύθυνση της δεύτερης καθέτου B(s) ή ισοδύναμα απομακρύνεται από το εγγύτατο επίπεδο.
στρέφεται προς την
διεύθυνση της δεύτερης καθέτου B(s) ή ισοδύναμα απομακρύνεται από το εγγύτατο επίπεδο.
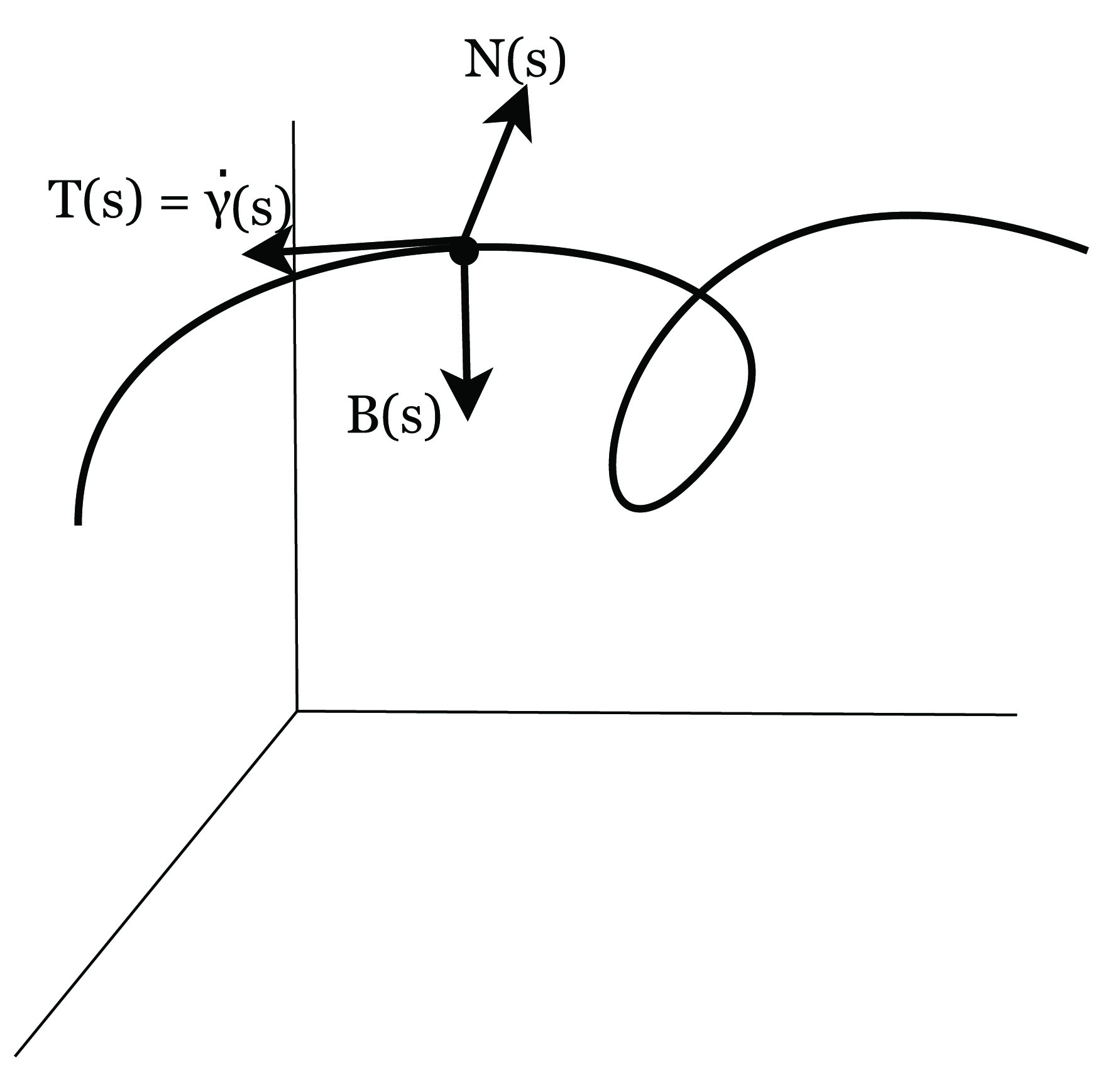
Πρόταση 1.4: ΄Εστω γ : I → ℝ3 καμπύλη Frenet. Τότε η στρέψη της γ δίνεται συναρτήσει των παραγώγων της από την σχέση
![.γ..
τ(s) = [γ˙(s)?γ(s)--(s)].
κ(s)2](02_chapter_01108x.png)
Απόδειξη. Η στρέψη της καμπύλης γ δίνεται από τον τύπο τ(s) = ⟨Ṅ(s),B(s)⟩, όπου
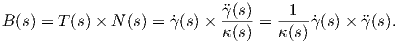
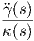 θα μας δώσει:
θα μας δώσει:
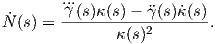
![..γ.(s)κ(s)- ?γ(s)˙κ(s) 1
τ(s) = ⟨N˙(s),B (s)⟩ = ⟨----------2-------,----˙γ(s)× ?γ (s)⟩
κ(s) κ(s)
= --1--(⟨.γ..(s),γ˙(s) × ?γ(s)⟩ - ⟨?γ(s)˙κ(s),-1--˙γ(s)× ?γ(s)⟩)
κ (s)2 κ (s)2 κ(s)
1 ... κ˙(s) 1
= ----2[γ (s)γ˙(s)?γ(s)]- [----2?γ(s)----˙γ(s)?γ(s)]
κ (s) ... κ(s) κ(s)
= [˙γ(s)?γ(s)γ(s)],
κ(s)2](02_chapter_01112x.png)
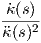
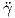 (s) και
(s) και 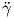 (s)
είναι συνεπίπεδα. ▄
(s)
είναι συνεπίπεδα. ▄
Θεώρημα 1.8: ΄Εστω γ : I → ℝ3 μια καμπύλη Frenet. Τότε το τρίεδρο Frenet ικανοποιεί το παρακάτω σύστημα συνήθων διαφορικών εξισώσεων:
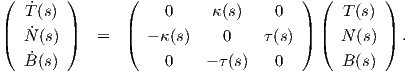
Απόδειξη. Η καμπύλη γ έχει παράμετρο το μήκος τόξου της s, επομένως η κύρια κάθετος θα δίνεται από
τον τύπο N(s) = 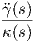 . ΄Ομως T(s) =
. ΄Ομως T(s) = 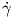 (s), οπότε Ṫ(s) =
(s), οπότε Ṫ(s) =  (s) άρα
(s) άρα
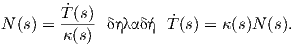
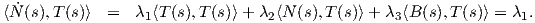
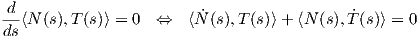
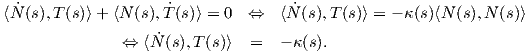
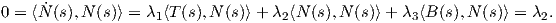
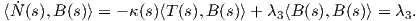
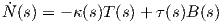
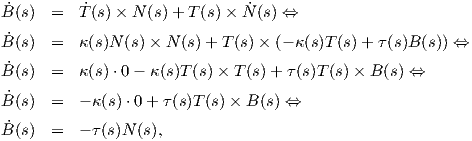
Αξίζει σε αυτό το σημείο να σημειώσουμε ότι οι τύποι του Frenet μπορούν να επαναδιατυπωθούν πιο απλά χρησιμοποιώντας το διάνυσμα περιστροφής του Darboux που ορίζεται από τη σχέση
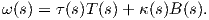
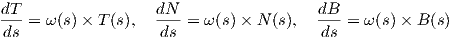
Θεώρημα 1.9: ΄Εστω γ : I → ℝ3 καμπύλη Frenet. Τότε η στρέψη τ : I → ℝ είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(I) της γ περιέχεται σε ένα επίπεδο.
Απόδειξη. ϒποθέτουμε πρώτα ότι η εικόνα της γ περιέχεται στο επίπεδο ⟨c,M⟩ = d, όπου M είναι ένα σταθερό μοναδιαίο διάνυσμα του ℝ3, d είναι μια αριθμητική σταθερά και το c ∈ ℝ3 ένα μη μηδενικό διάνυσμα. Μπορούμε να υποθέσουμε ότι το M είναι μοναδιαίο διάνυσμα. Παραγωγίζοντας δύο φορές τη ⟨γ(s),M⟩ = d, ως προς s, παίρνουμε:
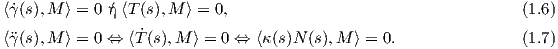
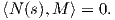 | (1.8) |
Από τις εξισώσεις (1.4) και (1.8) βλέπουμε ότι τα διανύσματα T(s) και N(s) είναι κάθετα στο M,
οπότε το διάνυσμα B(s) = T(s) × N(s) είναι παράλληλο με το M. Επειδή τα διανύσματα B(s) και
M είναι μοναδιαία και η απεικόνιση B : I → S2,s B(s) είναι λεία (άρα συνεχής) συνάρτηση του
s, πρέπει να έχουμε είτε B(s) = M για όλα τα s ∈ I είτε B(s) = -M για όλα τα s ∈ I. Σε κάθε
περίπτωση, το B(s) είναι σταθερό διάνυσμα, οπότε Ḃ(s) = 0, άρα τ = 0. Αντίστροφα, υποθέτουμε
ότι η στρέψη τ της γ είναι παντού μηδέν. Επειδή ισχύει Ḃ(s) = -τ(s)N(s), τότε Ḃ(s) = 0 άρα το
B(s) είναι ένα σταθερό διάνυσμα έστω B(s) = M. Τότε όμως για κάθε σημείο της καμπύλης είναι
B(s) είναι λεία (άρα συνεχής) συνάρτηση του
s, πρέπει να έχουμε είτε B(s) = M για όλα τα s ∈ I είτε B(s) = -M για όλα τα s ∈ I. Σε κάθε
περίπτωση, το B(s) είναι σταθερό διάνυσμα, οπότε Ḃ(s) = 0, άρα τ = 0. Αντίστροφα, υποθέτουμε
ότι η στρέψη τ της γ είναι παντού μηδέν. Επειδή ισχύει Ḃ(s) = -τ(s)N(s), τότε Ḃ(s) = 0 άρα το
B(s) είναι ένα σταθερό διάνυσμα έστω B(s) = M. Τότε όμως για κάθε σημείο της καμπύλης είναι
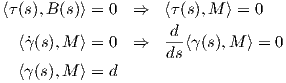
Από την απόδειξη του παραπάνω θεωρήματος συνεπάγεται ότι η εφαπτομένη και η πρώτη κάθετος βρίσκονται στο επίπεδο της καμπύλης, οπότε το εγγύτατο επίπεδο σε κάθε σημείο της καμπύλης ταυτίζεται με το επίπεδό της.
Ορισμός 1.15: Η καμπύλη γ : I → ℝ3 λέγεται γενικευμένη έλικα ή ισοκλινής καμπύλη, όταν οι εφαπτόμενές της σχηματίζουν σταθερή γωνία με σταθερό διάνυσμα του χώρου.
Παραδείγματα γενικευμένων ελίκων είναι όλες οι επίπεδες καπμύλες, αρκεί ως σταθερό διάνυσμα να θεωρείται το διάνυσμα το κάθετο στο επίπεδο της καμπύλης, οπότε η σταθερή γωνία θα είναι π∕2.
Απόδειξη. ΄Εστω ότι η γ είναι γενικευμένη έλικα μοναδιαίας ταχύτητας. ΄Εστω M το σταθερό διάνυσμα στον χώρο, που σχηματίζει σταθερή γωνία ω με το εφαπτόμενο διάνυσμα T της καμπύλης και χωρίς βλάβη της γενικότητας, υποθέτουμε ότι ∥M∥ = 1. ΄Εχουμε ⟨M,T(s)⟩ = cosω (σταθερό), για κάθε s ∈ I. Παραγωγίζοντας και λαμβάνοντας υπόψη τους τύπους του Frenet, έχουμε ότι
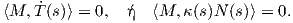
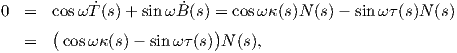
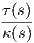 =
= 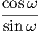 = cotω = c (σταθερά). Αντίστροφα, έστω
= cotω = c (σταθερά). Αντίστροφα, έστω  = c.
Εφόσον η συνάρτηση cotω παίρνει τιμές στο (-∞,+∞), μπορούμε να βρούμε ω, ώστε c = cotω. Επομένως,
έχουμε
= c.
Εφόσον η συνάρτηση cotω παίρνει τιμές στο (-∞,+∞), μπορούμε να βρούμε ω, ώστε c = cotω. Επομένως,
έχουμε 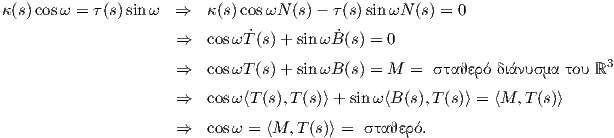
Πρόταση 1.6: ΄Εστω γ : I → ℝ3 μια επίπεδη καμπύλη μοναδιαίας ταχύτητας. Τότε η γ είναι τμήμα κύκλου εάν και μόνο εάν έχει σταθερή καμπυλότητα.
Απόδειξη. Αν η γ είναι τμήμα κύκλου κέντρου (x0,y0) και ακτίνας r, τότε δίνεται από τη σχέση
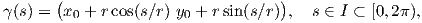
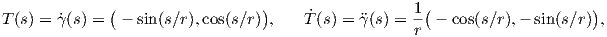
 , δηλαδή σταθερή.
, δηλαδή σταθερή.
Αντίστροφα, έστω ότι η καμπυλότητα είναι σταθερή, κ(s) = κ για κάθε s ∈ I. Θεωρούμε την καμπύλη
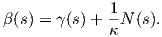
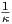 Ṅ(s) = T(s) +
Ṅ(s) = T(s) + 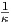 (-κT(s)) = 0. Επομένως, η β(s) είναι σταθερή, δηλαδή β(s) = (x0,y0)
και
(-κT(s)) = 0. Επομένως, η β(s) είναι σταθερή, δηλαδή β(s) = (x0,y0)
και
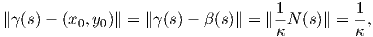
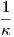 . ▄
. ▄
Παράδειγμα 1.2: ΄Εστω γ : I → ℝ3 μια κανονική καμπύλη μοναδιαίας ταχύτητας με αντίστοιχο τρίεδρο Frenet {T,N,B}, τέτοιο ώστε για κάθε s ∈ I το διάνυσμα
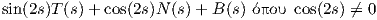
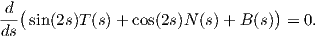
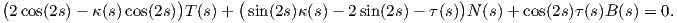
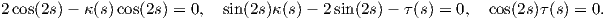
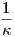 =
= 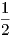 .
.
Θα δούμε τώρα ότι μια καμπύλη Frenet στον χώρο ℝ3 καθορίζεται από την καμπυλότητά της και τη στρέψη της (μη λαμβάνοντας υπόψη στερεές κινήσεις του ℝ3 που διατηρούν τον προσανατολισμό). Χρειαζόμαστε πρώτα τον εξής ορισμό:
Ορισμός 1.16: Μια απεικόνιση Φ : ℝ3 → ℝ3 ονομάζεται Ευκλείδεια (ή στερεά) κίνηση του ℝ3 (rigid motion), εάν έχει τη μορφή Φ(X) = AX + b, όπου b ∈ ℝ3 και
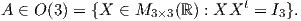
Θεώρημα 1.10: (Θεμελιώδες Θεώρημα της Θεωρίας καμπυλών)
΄Εστω κ : I → ℝ+ και τ : I → ℝ διαφορίσιμες συναρτήσεις. Τότε υπάρχει μια καμπύλη Frenet γ : I → ℝ3
η οποία να έχει καμπυλότητα κ και στρέψη τ. Επιπλέον, εάν 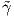 : I → ℝ3 είναι μια άλλη τέτοια καμπύλη,
τότε υπάρχει πίνακας A ∈ SO(3) και διάνυσμα b ∈ ℝ3 τέτοια ώστε
: I → ℝ3 είναι μια άλλη τέτοια καμπύλη,
τότε υπάρχει πίνακας A ∈ SO(3) και διάνυσμα b ∈ ℝ3 τέτοια ώστε
Η απόδειξη στηρίζεται στο θεμελιώδες θεώρημα ύπαρξης και μοναδικότητας λύσης συνήθων διαφορικών εξισώσεων με αρχική συνθήκη.
Παράδειγμα 1.3: (α) Δικαιολογήστε ότι υπάρχει καμπύλη γ με παράμετρο το μήκος τόξου της s, τέτοια ώστε
κ(s) = es και τ(s) = 2es.
(β) Για την προηγούμενη καμπύλη βρείτε όλα τα s ∈ ℝ για τα οποία ισχύει 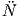 (s) = Ṅ(s) - 10N(s). Για το (α),
παρατηρούμε ότι κ(s) > 0 για κάθε s ∈ ℝ και οι συναρτήσεις κ(s), τ(s) είναι διαφορίσιμες. Επομένως, από το
προηγούμενο θεώρημα, υπάρχει καμπύλη γ με παραμέτρηση ως προς το μήκος τόξου για την οποία η
καμπυλότητα και η στρέψη δίνονται από τους τύπους κ(s) = es και τ(s) = 2es. Για το (β) έχουμε
Ṅ(s) = -κ(s)T(s) + τ(s)B(s) = -esT(s) + 2esB(s). Παραγωγίζοντας την προηγούμενη σχέση, παίρνουμε
(s) = Ṅ(s) - 10N(s). Για το (α),
παρατηρούμε ότι κ(s) > 0 για κάθε s ∈ ℝ και οι συναρτήσεις κ(s), τ(s) είναι διαφορίσιμες. Επομένως, από το
προηγούμενο θεώρημα, υπάρχει καμπύλη γ με παραμέτρηση ως προς το μήκος τόξου για την οποία η
καμπυλότητα και η στρέψη δίνονται από τους τύπους κ(s) = es και τ(s) = 2es. Για το (β) έχουμε
Ṅ(s) = -κ(s)T(s) + τ(s)B(s) = -esT(s) + 2esB(s). Παραγωγίζοντας την προηγούμενη σχέση, παίρνουμε
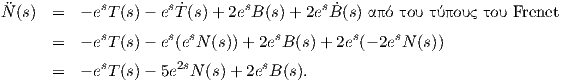
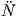 (s) = Ṅ(s) - 10N(s) θα έχουμε:
(s) = Ṅ(s) - 10N(s) θα έχουμε: 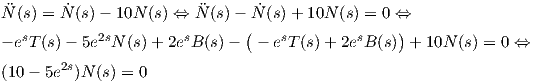
Ορισμός 1.17: ΄Εστω γ : I → ℝ3 μια κανονική καμπύλη του ℝ3 (όχι απαραίτητα με παραμέτρηση ως προς
το μήκος τόξου). ΄Εστω 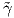 = γ ∘ h : J → ℝ3 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια
αμφιδιαφόριση h : J → I και έστω
= γ ∘ h : J → ℝ3 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια
αμφιδιαφόριση h : J → I και έστω 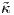 : J → ℝ η καμπυλότητα της
: J → ℝ η καμπυλότητα της 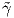 . Για κάθε t ∈ I η καμπυλότητα της
καμπύλης γ στο σημείο t είναι ο αριθμός
. Για κάθε t ∈ I η καμπυλότητα της
καμπύλης γ στο σημείο t είναι ο αριθμός
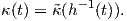
Παρόμοια, ορίζουμε τη στρέψη τ : I → ℝ της γ ως
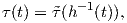
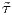 : J → ℝ η στρέψη της
: J → ℝ η στρέψη της 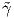 .
.
Χρησιμοποιώντας τους παραπάνω ορισμούς, είναι δυνατόν να προκύψουν τύποι για την καμπυλότητα και στρέψη καμπύλης αναφερομένης σε τυχαία παράμετρο.
Απόδειξη. ΄Εστω 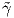 = γ ∘h : J → ℝ3 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s-1 και s
η συνάρτηση μήκους τόξου. ΄Εστω
= γ ∘h : J → ℝ3 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s-1 και s
η συνάρτηση μήκους τόξου. ΄Εστω 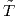 ,Ñ,
,Ñ,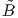 το τρίεδρο Frenet της
το τρίεδρο Frenet της 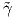 . Τότε γ =
. Τότε γ = 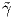 ∘h-1 ή γ =
∘h-1 ή γ = 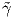 ∘s, οπότε για κάθε
t ∈ I έχουμε:
∘s, οπότε για κάθε
t ∈ I έχουμε:
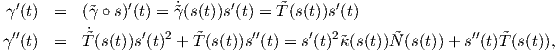
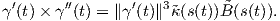
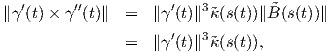
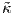 (s(t)) =
(s(t)) = 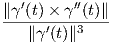 , άρα απο τον Ορισμό 1.17 έχουμε τον ζητούμενο τύπο για την καμπυλότητα της
γ:
, άρα απο τον Ορισμό 1.17 έχουμε τον ζητούμενο τύπο για την καμπυλότητα της
γ:
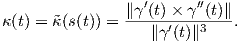
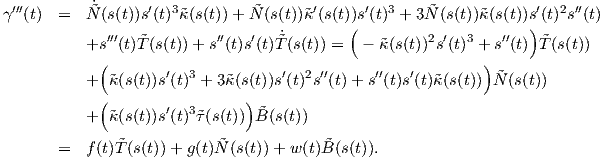
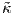 (s(t)) =
(s(t)) = 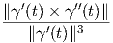 , οπότε με αντικατάσταση στη
σχέση (1.11) θα πάρουμε
, οπότε με αντικατάσταση στη
σχέση (1.11) θα πάρουμε
![⟨γ′(t) × γ′′(t),γ′′′(t)⟩ [γ′(t)γ′′(t)γ ′′′(t)]
˜τ(s(t)) = -----′-----′′---2-- = ---′-----′′---2 .
∥γ (t)× γ (t)∥ ∥γ (t)× γ (t)∥](02_chapter_01189x.png)
![′ ′′ ′′′
τ(t) = ˜τ(s(t)) = [γ-(t)γ-(t)γ-(t)].
∥γ′(t)× γ′′(t)∥2](02_chapter_01190x.png)
Εύκολα αποδεικνύεται ότι για μια κανονική καμπύλη γ : I → ℝ3 θετικής καμπυλότητας και τυχαία παράμετρο, τα διανύσματα του τριέδρου Frenet σε κάποιο σημείο t ∈ I δίνονται από τους παρακάτω τύπους:
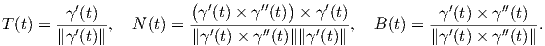
Πρόταση 1.8: ΄Εστω γ : I → ℝ3 μια κανονική καμπύλη με τυχαία παράμετρο και θετική καμπυλότητα. ΄Εστω {T(t),N(t),B(t)} το τρίεδρο Frenet της γ. Τότε οι παράγωγοι των T,N,B δίνονται ως
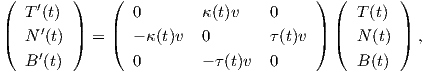
Η απόδειξη αφήνεται ως άσκηση.
Πόρισμα 1.2: ΄Εστω γ : I → ℝ3 κανονική καμπύλη του ℝ3. Τότε:
Παράδειγμα 1.4: Θεωρούμε την κυκλοειδή καμπύλη του επιπέδου με παραμέτρηση γ(t) = α(t,1)+α(-sint,-cost) (α > 0).
Λύση
1. Θέτοντας γ(t) = (x(t),y(t)), παίρνουμε τις εξισώσεις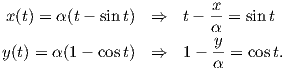
 t -
t -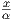
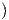 2 +
2 + 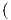 1 -
1 -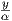
 2 = 1 και (αt - x)2 + (α - y)2 = α2. Η εξίσωση αυτή είναι οικογένεια κύκλου με
κέντρο τα σημεία K(αt,α) και σταθερής ακτίνας α > 0. Η εικόνα της φαίνεται στο Σχήμα 1.11.
2 = 1 και (αt - x)2 + (α - y)2 = α2. Η εξίσωση αυτή είναι οικογένεια κύκλου με
κέντρο τα σημεία K(αt,α) και σταθερής ακτίνας α > 0. Η εικόνα της φαίνεται στο Σχήμα 1.11.
2. Είναι γ′(t) = α(1 - cost,sint) άρα
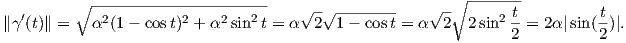
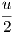 du = 4α(1 - cos
du = 4α(1 - cos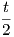 ).
).
3. Η καμπύλη είναι κανονική εκτός εάν γ′(t) = 0 δηλαδή cost = 1 και sint = 0, δηλαδή για t = 2kπ (k ∈ ℤ).
Παράδειγμα 1.5: ΄Εστω γ : I → ℝ2 η καμπύλη γ(t) = (sint,sin(2t)). Είναι η γ κανονική, απλή ή κλειστή;
Λύση
Η γ είναι κανονική, επειδή γ′(t) = (cost,2cos(2t))≠(0,0) για κάθε t. Η καμπύλη δεν είναι απλή, επειδή γ(0) = γ(π) = (0,0) (δηλαδή η γ έχει αυτοτομές). Τέλος, η γ είναι κλειστή, διότι για I = [0,2π] γ(0) = γ(2π) = (0,0). Το ίχνος της φαίνεται παρακάτω: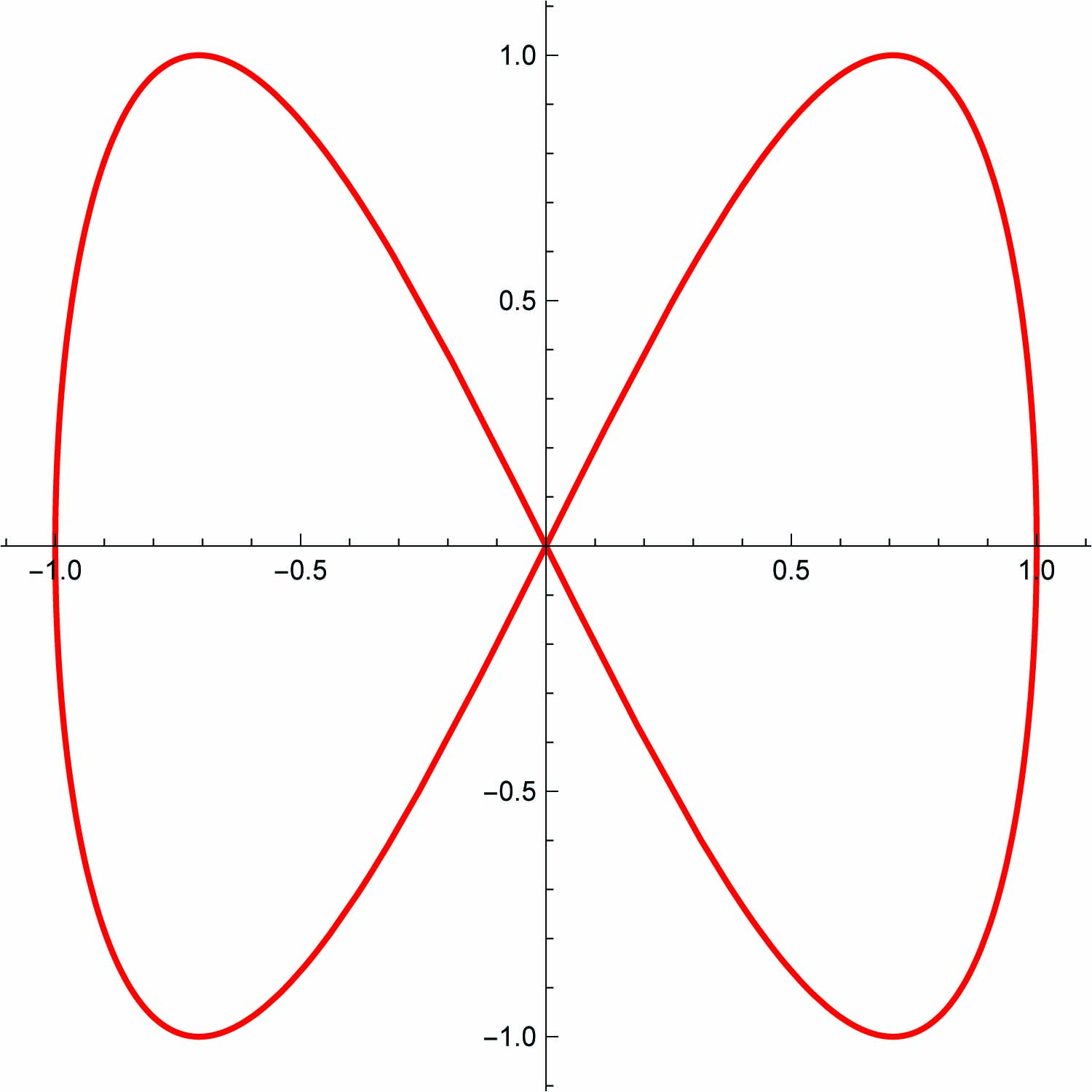
Παράδειγμα 1.6: Θεωρούμε την καμπύλη γ(t) = (t,cosht),t > 0. Βρείτε την ταχύτητα ∥γ′(t)∥ της γ και χρησιμοποιήστε τη για να κάνετε αναπαραμέτρηση της γ ως προς το μήκος τόξου.
Λύση
Είναι γ′(t) = (1,sinht) άρα ∥γ′(t)∥ =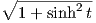 = cosht. ΄Εστω
= cosht. ΄Εστω
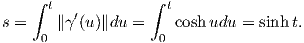
 =
= 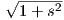 . Συνεπώς, η
αναπαραμέτρηση της γ ως προς το μήκος τόξου είναι η
. Συνεπώς, η
αναπαραμέτρηση της γ ως προς το μήκος τόξου είναι η
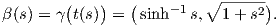
Παράδειγμα 1.7: α) ϒπολογίστε τις καμπυλότητες κ1,κ2 και τις στρέψεις τ1,τ2 των ελίκων γ1,γ2 : ℝ → ℝ3

Λύση
α) Για τις καμπυλότητες θα χρησιμοποιήσουμε τον τύπο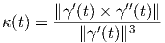
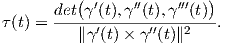
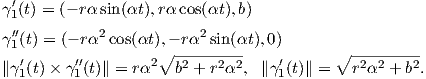
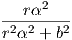 =
= 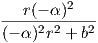 = κ2(t). Επίσης, τ1(t) =
= κ2(t). Επίσης, τ1(t) = 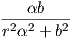 = τ2(t).
= τ2(t).
β) ΄Εστω A είναι ο πίνακας της γραμμικής απεικόνισης Φ : ℝ3 → ℝ3. Αρκεί να λύσουμε την εξίσωση
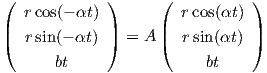
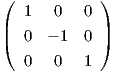 . ΄Αρα η Φ : ℝ3
→ ℝ3 έχει τύπο
Φ(x,y,z) = (x,-y,z). Επειδή det(A) = -1, η Φ δεν διατηρεί τον πρασανατολισμό.
. ΄Αρα η Φ : ℝ3
→ ℝ3 έχει τύπο
Φ(x,y,z) = (x,-y,z). Επειδή det(A) = -1, η Φ δεν διατηρεί τον πρασανατολισμό.
Παράδειγμα 1.8: Αποδείξτε ότι η καμπύλη γ : (-π∕2,π∕2) → ℝ3,γ(t) = (2cos2t- 3,sint- 8,3sin2t + 4) είναι κανονική. Ελέξτε κατά πόσον το ίχνος της γ είναι
Λύση
Είναι γ′(t) = (-4costsint,cost,6sintcost)≠(0,0,0) για κάθε t ∈ (-π∕2,π∕2) (επειδή cost≠0). ΄Αρα η γ είναι κανονική καμπύλη. ϒπολογίζουμε ότι det γ′(t),γ′′(t),γ′′′(t)
γ′(t),γ′′(t),γ′′′(t) = 0 άρα τ(t) = 0, συνεπώς η καμπύλη είναι επίπεδη.
Τα διανύσματα γ′(t) και γ′′(t) είναι γραμμικώς ανεξάρτητα (δείχνοντας π.χ. ότι γ′(t) × γ′′(t)≠
= 0 άρα τ(t) = 0, συνεπώς η καμπύλη είναι επίπεδη.
Τα διανύσματα γ′(t) και γ′′(t) είναι γραμμικώς ανεξάρτητα (δείχνοντας π.χ. ότι γ′(t) × γ′′(t)≠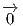 ) άρα κ(t)≠0,
οπότε η γ δεν είναι τμήμα ευθείας.
) άρα κ(t)≠0,
οπότε η γ δεν είναι τμήμα ευθείας.
Λύση
(I) ΄Εστω ότι έχουμε την καμπύλη γ : I → ℝ3 με παράμετρο το μήκος τόξου της. ΄Ενα σημείο (x,y,z) ∈ ℝ3 είναι σημείο του εγγύτατου επιπέδου στο σημείο γ(s0) εάν και μόνο εάν η διαφορά (x,y,z) - γ(s0) ανήκει στον υπόχωρο που παράγουν τα διανύσματα T(s0) και N(s0), δηλαδή είναι κάθετη στο B(s0). ΄Αρα τα σημεία (x,y,z) του εγγύτατου επιπέδου στο γ(s0) ικανοποιούν την σχέση Επειδή B(s0) = T(s0) × N(s0) =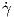 (s0) ×
(s0) ×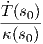 =
= 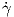 (s0) ×
(s0) ×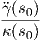 , η σχέση (1.12) ισοδυναμεί με
την
, η σχέση (1.12) ισοδυναμεί με
την
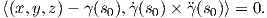
(II) ΄Εστω τώρα ότι έχουμε μια κανονική καμπύλη a : I → ℝ3 όχι κατ′ αναγκή μοναδιαίας ταχύτητας. Τα σημεία (x,y,z) του εγγύτατου επιπέδου στο a(t0) ικανοποιούν την αντίστοιχη σχέση (1.12) δηλαδή
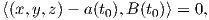
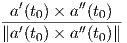 , παίρνουμε τη συνθήκη
, παίρνουμε τη συνθήκη
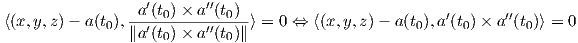
Παράδειγμα 1.10: Αν η καμπύλη γ : I → ℝ3 έχει παράμετρο το μήκος τόξου της και σταθερή στρέψη τ≠0, να δείξετε ότι η καμπύλη
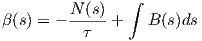
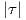 .
.
Λύση
΄Εχουμε β′(s) = -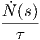 + B(s) και επειδή Ṅ(s) = -κ(s)T(s) + τB(s), θα είναι β′(s) =
+ B(s) και επειδή Ṅ(s) = -κ(s)T(s) + τB(s), θα είναι β′(s) = 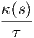 T(s). Παρατηρούμε
ότι ∥β′(s)∥ =
T(s). Παρατηρούμε
ότι ∥β′(s)∥ = 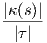 ≠1 δηλαδή η παράμετρος s για την καμπύλη β είναι τυχαία, οπότε η καμπυλότητα θα δίνεται
από τον τύπο
≠1 δηλαδή η παράμετρος s για την καμπύλη β είναι τυχαία, οπότε η καμπυλότητα θα δίνεται
από τον τύπο
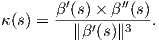
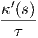 T(s) +
T(s) + 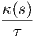 Ṫ(s), οπότε
Ṫ(s), οπότε 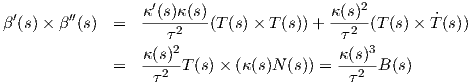
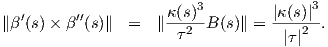
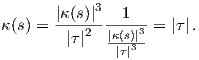
Παράδειγμα 1.11: ΄Εστω β : ℝ → ℝ3 κανονική καμπύλη μοναδιαίας ταχύτητας τέτοια ώστε η εφαπτομένη σε κάθε σημείο β(s) περνά από σταθερό σημείο p ∈ ℝ3. Δείξτε ότι η καμπύλη β είναι ευθεία.
Λύση
Η εφαπτομένη στο σημείο β(s) δίνεται από την εξίσωση β(s) + t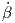 (s). Αφού το σημείο p ανήκει σε αυτήν την ευθεία
για κάθε s ∈ ℝ, υπάρχει συνάρτηση f(s) τέτοια ώστε
(s). Αφού το σημείο p ανήκει σε αυτήν την ευθεία
για κάθε s ∈ ℝ, υπάρχει συνάρτηση f(s) τέτοια ώστε
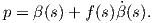
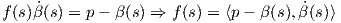
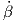 (s) και
έχουμε
(s) και
έχουμε
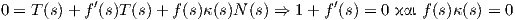
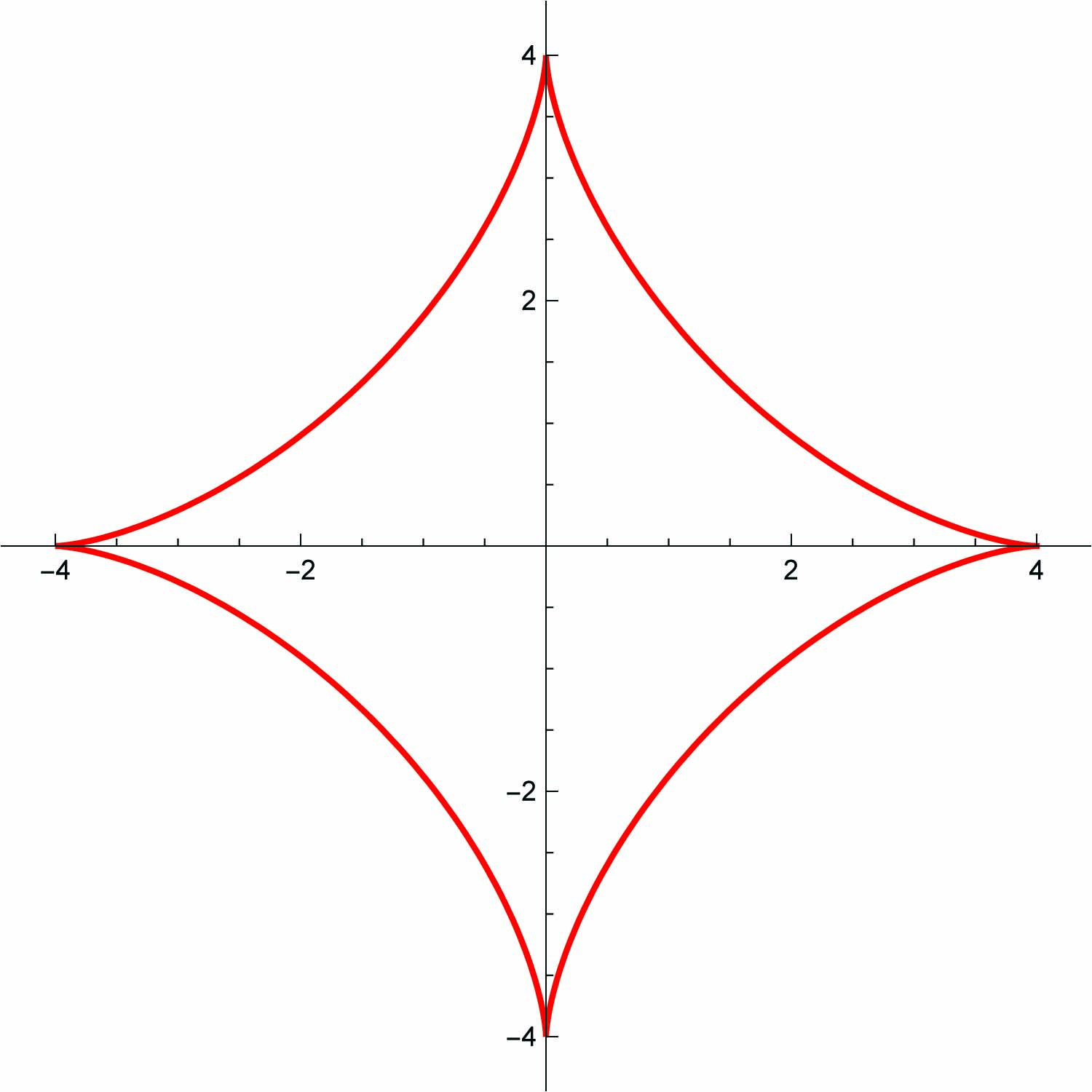
1. Η αστεροειδής καμπύλη είναι η καμπύλη του επιπέδου με παραμέτρηση γ : ℝ → ℝ2, γ(t) = (4α cos3t,4α sin3t) = 3α(cost,sint)+ α(cos(3t),-sin(3t)), α > 0.
 du.
du.
2. Δίνεται η καμπύλη γ(t) = (e-t cost,e-t sint), t ∈ ℝ.
3. Δίνονται οι καμπύλες γ1,γ2 : ℝ → ℝ2 με γ1 = r(cos(αt),sin(αt)), γ2 = r(cos(-αt),sin(-αt)). ϒπολογίστε τις καμπυλότητες κ1,κ2 των γ1,γ2 αντίστοιχα. Βρείτε μια στερεά κίνηση Φ : ℝ2 → ℝ2 τέτοια ώστε γ2 = Φ ∘ γ1. Διατηρεί η Φ τον προσανατολισμό;
4. ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου και με πλαίσιο Frenet
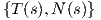 . Για λ ∈ ℝ ορίζουμε την παράλληλη καμπύλη
. Για λ ∈ ℝ ορίζουμε την παράλληλη καμπύλη
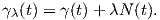
5. ΄Εστω γ : I → ℝ2 μια κανονική καμπύλη του ℝ2. Αποδείξτε ότι η καμπυλότητα ικανοποιεί την σχέση
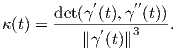
6. ΄Εστω γ : I → ℝ2 η καμπύλη του ℝ2 με γ(t) = (sint,sin(2t)). Είναι η γ κανονική, απλή και κλειστή;
7. ΄Εστω ότι η απεικόνιση γ : ℝ → ℝ2 είναι μια παραμέτρηση ως προς το μήκος τόξου μιας θετικά προσανατολισμένης, απλής και κλειστής καμπύλης. Δείξτε ότι αν η περίοδος της γ είναι L > 0, τότε η καμπυλότητα κ(s) της γ ικανοποιεί τη σχέση
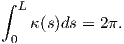
Το ολοκλήρωμα στο αριστερό μέλος ονομάζεται ολική καμπυλότητα της γ.
8. ϒπολογίστε τις καμπυλότητες κ1,κ2 και τις στρέψεις τ1,τ2 των ελίκων γ1,γ2 : ℝ → ℝ3 με γ1(t) = (r cos(at),r sin(at),bt) και γ2(t) = (r cos(-at),r sin(-at),bt) , (r,a,b > 0). Βρείτε μια στερεά κίνηση Φ : ℝ3 → ℝ3 τέτοια ώστε γ2 = Φ ∘ γ1. Διατηρεί η Φ τον προσανατολισμό;
9. Βρείτε μια κανονική καμπύλη γ : ℝ → ℝ3 με σταθερή καμπυλότητα k > 0 και σταθερή στρέψη τ ∈ ℝ.
10. Αποδείξτε ότι η στρέψη τ μιας κανονικής καμπύλης γ : ℝ → ℝ3 ικανοποιεί τη σχέση
![[γ ′(t),γ′′(t),γ′′′(t)]
τ (t) = ---′------′′---2--.
∥γ (t) × γ (t)∥](02_chapter_01250x.png)
11. Αποδείξτε ότι η καμπύλη γ : (-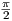 ,
,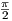 ) → ℝ3 με γ(t) = (2cos2t - 3,sint - 8,3sin2t + 4) είναι κανονική.
Ελέγξτε κατά πόσον το ίχνος της γ περιέχεται σε: α) μια ευθεία του ℝ3, β) ένα επίπεδο του ℝ3.
) → ℝ3 με γ(t) = (2cos2t - 3,sint - 8,3sin2t + 4) είναι κανονική.
Ελέγξτε κατά πόσον το ίχνος της γ περιέχεται σε: α) μια ευθεία του ℝ3, β) ένα επίπεδο του ℝ3.
12. Το ίδιο ερώτημα όπως στην ΄Ασκηση 4 για την καμπύλη γ : ℝ → ℝ3, γ(t) = (t3 + t2 + 3,t3 -t + 1,t2 + t + 1).
13. Αναζητήστε στη βιβλιογραφία μια απόδειξη του θεωρήματος του Fenchel: ΄Εστω ότι η απεικόνιση γ : ℝ → ℝ3 είναι μια κανονική παραμέτρηση μιας κλειστής καμπύλης στον ℝ3 με παράμετρο το μήκος τόξου. Τότε ισχύει
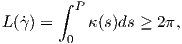
14. Αναζητήστε στην βιβλιογραφία μια απόδειξη του Θεμελιώδους Θεωρήματος της Θεωρίας Καμπυλών.
15. ΄Εστω γ : ℝ → ℝ3 μια κανονική καμπύλη με παράμετρο το μήκος τόξου της, για την οποία υπάρχει παραγωγίσιμη απεικόνιση φ : ℝ → ℝ, ώστε
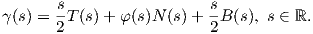
 ,0,0), να υπολογίσετε την καμπυλότητα, τη στρέψη της γ, καθώς και τη συνάρτηση φ.
,0,0), να υπολογίσετε την καμπυλότητα, τη στρέψη της γ, καθώς και τη συνάρτηση φ.
16. ΄Εστω α : ℝ → ℝ3 κανονική καμπύλη μοναδιαίας ταχύτητας τέτοια ώστε κ(s)≠0 για κάθε s ∈ ℝ. Να δείξετε ότι η καμπύλη α είναι επίπεδη εάν και μόνο έαν όλα τα εγγύτατα επίπεδά της περνούν από σταθερό σημείο p.
[1] M. Abate and F. Torena, Curves and Surfaces, Springer 2012.
[2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press 2010.
[3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall 1976.
[4] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, 2011. Μετάφραση 3ης εκδ. Dianusmatik�c Logism�c, Πανεπιστημιακές Εκδόσεις Κρήτης, 1992.
[5] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, 2007.
[6] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, 2013.
[7] A. Pressley, Elementary Differential Geometry, Second Edition, Springer 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.