 |
 |
| 8 | 'ΓΡΑΦΙΚΑ ΚΑΙ ΕΙΚΟΝΙΚΗ ΠΡΑΓΜΑΤΙΚΟΤΗΤΑ' | Μουστάκας Κ., Παλιόκας Ι., Τσακίρης A., Τζοβάρας Δ. |
 |
 |


Πατήστε πάνω στους τίτλους των υποκεφαλαίων ή μεταφερθείτε στην αρχική σελίδα.
|
2015 |
|
ΚΕΦΑΛΑΙΟ 8: ΣΥΝΘΕΤΙΚΗ ΚΙΝΗΣΗ
|
|
|
ΣύνοψηΗ συνθετική κίνηση είναι ένα θεμελιώδες στοιχείο των σύγχρονων ρεαλιστικών συστημάτων γραφικών. Είτε πρόκειται για απλή μεταφορά αντικειμένων, είτε για σκελετική κίνηση εικονικών ανθρώπων είτε για πολύπλοκη κίνηση δυναμικών συστημάτων, έχει τις ρίζες της στους 3Δ γεωμετρικούς μετασχηματισμούς και στην υλοποίηση των νόμων της φυσικής. Το παρόν κεφάλαιο αποτελεί εισαγωγή στη συνθετική κίνηση μέσω της περιγραφής της κίνησης βάσει καρέ-κλειδιών, της σκελετικής κίνησης αλλά και της προσομοίωσης δυναμικών συστημάτων βάσει μοντέλων που υλοποιούν προσεγγιστικά τους νόμους της φυσικής και συγκεκριμένα της κλασικής μηχανικής. Προαπαιτούμενη γνώσηΑπαιτούνται βασικές γνώσεις ως υπόβαθρο σε θέματα γραμμικής άλγεβρας, διανυσματικής ανάλυσης, φυσικής και ειδικότερα κλασικής μηχανικής. Από το περιεχόμενο εντός του βιβλίου, απαιτούνται γνώσεις γεωμετρικών μετασχηματισμών και προβολών (Κεφ. 3), αναπαράστασης 3Δ αντικειμένων (Κεφ. 4) και διαχείρισης σκηνής (Κεφ. 7). |
Όταν δούμε σε γρήγορη εναλλαγή μια ακολουθία εικόνων της ίδιας σκηνής, οι οποίες έχουν ληφθεί σε διαφορετικές χρονικές στιγμές, τότε έχουμε την αίσθηση ή καλύτερα την ψευδαίσθηση ότι τα αντικείμενα των εικόνων κινούνται. Αυτή η διαδικασία δε χρειάζεται να εμπλέκει χρήση υπολογιστή, όπως στην περίπτωση του παραδοσιακού αναλογικού κινηματογράφου. Οι ξεχωριστές εικόνες ονομάζονται καρέ και το σύνολό τους ακολουθία συνθετικής κίνησης (animation).
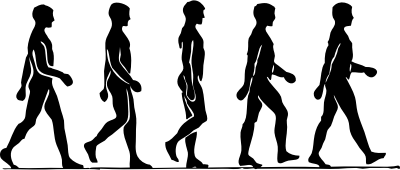
Στη συνέχεια του κεφαλαίου παρουσιάζονται κάποιες θεμελιώδεις μέθοδοι για την περιγραφή και υλοποίηση της κίνησης στις τρεις διαστάσεις. Δύο είναι οι βασικοί τρόποι για να επιτευχθεί αυτό. Ο πρώτος είναι με παρεμβολή βάσει καρέ κλειδιών και ο δεύτερος με χρήση προσομοίωσης των νόμων της φυσικής. Η πρώτη μέθοδος είναι η πιο κλασική περίπτωση που χρησιμοποιείται ευρύτατα σε διάφορους τομείς όπως ο σύγχρονος κινηματογράφος. Στη συνθετική κίνηση βάσει καρέ κλειδιών, ένας ειδικός (3Dartist) αναλαμβάνει να σχεδιάσει στον υπολογιστή τη θέση των αντικειμένων μιας σκηνής σε κάποιες χαρακτηριστικές στιγμές στο χρόνο. Αυτές οι στιγμές αντιστοιχούν στα καρέ-κλειδιά (key-frames). Στη συνέχεια εκτελείται παρεμβολή βάσει των δύο γειτονικών καρέ-κλειδιών (ένα μπροστά στο χρόνο και ένα πίσω) για τον αυτόματο υπολογισμό της θέσης των αντικειμένων σε όλες τις ενδιάμεσες χρονικές στιγμές. Στην Εικόνα 8.1 παρουσιάζεται ένα παράδειγμα συνθετικής σκελετικής κίνησης βάσει καρέ-κλειδιών.
Εικόνα 8.1. Δύο στιγμιότυπα σκελετικής κίνησης εικονικού χαρακτήρα
Στην περίπτωση, όμως, πολύπλοκων συστημάτων όπως η προσομοίωση ρευστών, ή πολλαπλών αντικειμένων σε σύγκρουση είναι δύσκολο και να σχεδιάσει κάποιος ειδικός ένα συγκεκριμένο καρέ-κλειδί, αλλά και να εκτιμηθεί μια ενδιάμεση κατάσταση με παρεμβολή. Στις περιπτώσεις αυτές υλοποιούνται οι νόμοι της φυσικής και στη συνέχεια τα αντικείμενα της σκηνής αφήνονται να τους υπακούσουν, ακολουθώντας τους κανόνες των δυναμικών συστημάτων. Ο τρόπος αυτός απόδοσης συνθετικής κίνησης δίνει ιδιαίτερα εντυπωσιακά αποτελέσματα αλλά έχει και πολλές δυσκολίες και περιορισμούς που θα συζητηθούν στο αντίστοιχο κεφάλαιο. Η Εικόνα 8.2 δείχνει ένα παράδειγμα προσομοίωσης ενός συνόλου συγκρουόμενων αντικειμένων.
Εικόνα 8.2. Παραδείγματα προσομοίωσης συγκρουόμενων αντικειμένων
Έστω ότι θέλουμε να μοντελοποιήσουμε ένα κινούμενο αυτοκίνητο. Όπως έχουμε δει σε προηγούμενο κεφάλαιο, ένα τρισδιάστατο αντικείμενο περιγράφεται από ένα σύνολο σημείων (κορυφές), τα οποία συνδέονται ανά τρία μεταξύ τους φτιάχνοντας έτσι στοιχειώδεις επιφάνειες (τρίγωνα) το σύνολο των οποίων ορίζει την επιφάνεια του αντικειμένου. Έστω ακόμα ότι ο χρήστης ενός συστήματος γραφικών (animator), που θέλει να συνθέσει κίνηση, έχει δημιουργήσει αντίγραφα του ίδιου αντικειμένου σε διαφορετικές θέσεις στο χώρο στις οποίες πρέπει το αυτοκίνητο να βρίσκεται σε προδιαγεγραμμένες χρονικές στιγμές (Εικόνα 8.3).
Το μόνο που μεταβάλλεται στο μοντέλο του αυτοκινήτου καθώς αυτό κινείται στο εικονικό περιβάλλον είναι οι θέσεις των κορυφών του και όχι η λίστα των τριγώνων. Έστω, λοιπόν, η θέση κάθε κορυφής:
{Εξ. 8.1} |
όπου Ν το σύνολο των κορυφών του αντικειμένου. Η θέση των κορυφών του αντικειμένου είναι γνωστή μόνον τις χρονικές στιγμές t0, t1, t2. Τα καρέ αυτά αποτελούν τα καρέ-κλειδιά της προσομοίωσης. Είναι προφανές ότι ο σχεδιασμός κάθε καρέ χειροκίνητα, θέτοντας δηλαδή τη θέση κάθε κορυφής με το χέρι, είναι ασύμφορος αν σκεφτούμε ότι για μια ρεαλιστική συνθετική κίνηση απαιτείται να έχουμε τουλάχιστον 25 καρέ ανά δευτερόλεπτο. Τι μπορούμε να κάνουμε για να αντιμετωπίσουμε το πρόβλημα αυτό;
Μια πολύ απλή και ευρύτατα χρησιμοποιούμενη λύση είναι η χρήση παρεμβολής για τον υπολογισμό της θέσης των αντικειμένων στα ενδιάμεσα καρέ των καρέ-κλειδιών. Έτσι, ενώ έχουμε ορίσει χειροκίνητα τη θέση του αντικειμένου στα καρέ-κλειδιά, όλα τα ενδιάμεσα καρέ μπορούν να υπολογιστούν με τη χρήση μιας συνάρτησης παρεμβολής.
Στη συνθετική κίνηση βάσει καρέ-κλειδιών είναι ιδιαίτερα σημαντικό να επιλέξουμε σωστά τη μεταβλητή την οποία θα μεταβάλουμε στο χρόνο (π.χ. θέση, προσανατολισμός) αλλά και την κατάλληλη συνάρτηση παρεμβολής.
Εικόνα 8.3. Καρέ-κλειδιά ενός συγκεκριμένου αντικειμένου για τρεις διαφορετικές χρονικές στιγμές
Η μία από τις δύο βασικότερες μεταβλητές που χρησιμοποιείται στη συνθετική κίνηση είναι η θέση ενός αντικειμένου. Ο πιο κλασικός τρόπος για τον υπολογισμό της θέσης ενός αντικειμένου τη χρονική στιγμή t βάσει της θέσης του τις χρονικές στιγμές t0 και t1 είναι η παρεμβολή.
{Εξ. 8.2} |
όπου η μεταβλητή α μπορεί να μεταβάλλεται γραμμικά ως προς το χρόνο, οπότε έχουμε γραμμική παρεμβολή:
{Εξ. 8.3} |
Η παραπάνω σχέση αφορά μια κορυφή του μοντέλου. Μια λύση να επεκταθεί η διαδικασία αυτή σε όλο το αντικείμενο είναι να εφαρμοστεί σε κάθε κορυφή του αντικειμένου.
{Εξ. 8.4} |
Μια άλλη λύση είναι να μην πειράξουμε την εξίσωση παρεμβολής αλλά να αλλάξουμε την είσοδο και την έξοδό της. Για παράδειγμα, αντί να χειριζόμαστε κάθε σημείο ενός αντικειμένου ξεχωριστά μπορούμε να το αναπαραστήσουμε ως ένα διάνυσμα κατάστασης μεγέθους 3Ν που θα περιέχει τις συντεταγμένες όλων των κορυφών.
{Εξ. 8.5} |
Ένα παράδειγμα για την περίπτωση του αυτοκινήτου παρουσιάζεται στην Εικόνα 8.4.
Στην πράξη ο τρόπος με τον οποίο υλοποιείται η συνθετική κίνηση είναι μέσω των μετασχηματισμών. Άρα έστω ο 4xN ομογενής πίνακας C, του οποίου τα διανύσματα-στήλη αντιστοιχούν στις ομογενείς συντεταγμένες καθεμίας από τις Ν κορυφές του.
{Εξ. 8.6} |
Έστω και ο ομογενής πίνακας μεταφοράς, του οποίου το διάνυσμα-στήλη που αντιστοιχεί στη μεταφορά μεταβάλλεται με το χρόνο
{Εξ. 8.7} |
Οπότε η μεταφορική κίνηση του αντικειμένου στο χρόνο περιγράφεται από την παρακάτω σχέση:
{Εξ. 8.8} |
Εικόνα 8.4. Συνθετική κίνηση βάσει καρέ -κλειδιών ενός αυτοκινήτου, το οποίο μεταφέρεται πάνω σε μία ευθεία γραμμή
Η δεύτερη πολύ σημαντική μεταβλητή που χρησιμοποιείται στη συνθετική κίνηση είναι η περιστροφή. Έστω στην περίπτωση αυτή ο ομογενής πίνακας περιστροφής Α(t) που κωδικοποιεί την περιστροφή γύρω από συγκεκριμένο άξονα περιστροφής. Στην περίπτωση αυτή η περιστροφική κίνηση περιγράφεται από την παρακάτω σχέση.
{Εξ. 8.9} |
Στην παρακάτω εικόνα παρουσιάζεται η περιστροφική κίνηση βάσει καρέ κλειδιών ενός αντικειμένου.
Εικόνα 8.5. Συνθετική κίνηση βάσει καρέ-κλειδιών ενός αυτοκινήτου, το οποίο περιστρέφεται γύρω από το κέντρο βάρους του
Πολλές φορές, ενώ θα θέλαμε να χειριστούμε ένα αντικείμενο ως συμπαγές, είναι απαραίτητο να συνθέσουμε κίνηση για τα επιμέρους τμήματά του. Για παράδειγμα στην περίπτωση του αυτοκινήτου πρέπει να ανοίξει μια πόρτα και στη συνέχεια και το παράθυρο. Μια πιο κλασική περίπτωση είναι αυτή ενός εικονικού χαρακτήρα. Κάποια αντικείμενα, λοιπόν, μπορούμε να τα θεωρήσουμε ως ένα σύνολο αντικειμένων τα οποία είναι μεν συμπαγή, αλλά μετασχηματίζονται σε σχέση με τα υπόλοιπα ανάλογα με τη δομή του ενιαίου αντικειμένου.
Ένας τρόπος για την αποδοτική οργάνωση ενός τέτοιου συνόλου αντικειμένων είναι η χρήση ενός μικρού γράφου σκηνής. Έτσι στη ρίζα του γράφου βρίσκεται όλο το αντικείμενο, ενώ τα παιδιά του ορίζουν τα διακριτά υποσύνολά του. Η διαδικασία αυτή επαναλαμβάνεται αναδρομικά. Έτσι στο τέλος έχουμε τους κόμβους-φύλλα, τα οποία αντιστοιχούν σε τμήματα που είναι συμπαγή και δεν έχουν επιπλέον τμήματα. Στα φύλλα αποθηκεύονται και οι κορυφές του αντίστοιχου τμήματος.
Η δομή αυτή αποκαλείται «αρθρωτό συμπαγές μοντέλο» διότι οι ακμές του γράφου σκηνής αντιστοιχούν στις αρθρώσεις/συνδέσεις του πραγματικού μοντέλου. Στην περίπτωση του αυτοκινήτου μια τέτοια άρθρωση αποτελούν οι μεντεσέδες της πόρτας. Για ένα ανθρωποειδές, συνδέσεις αποτελούν οι αρθρώσεις όπως οι ώμοι τα γόνατα, κ.ά. Στην παρακάτω εικόνα παρουσιάζεται ένα παράδειγμα ενός ανθρωποειδούς αρθρωτού αντικειμένου.
Όπως ακριβώς και στο γράφο σκηνής έτσι και στα αρθρωτά μοντέλα ο μετασχηματισμός κάθε κόμβου-γονέα «κληρονομείται» και στα παιδιά του διότι για την εύρεση του τοπικού συστήματος συντεταγμένων κάθε συμπαγούς τμήματος του μοντέλου γίνεται πολλαπλασιασμός όλων των πινάκων μετασχηματισμού των κόμβων οι οποίοι βρίσκονται στη διαδρομή που ενώνει τον εν λόγω κόμβο με τη ρίζα. Άρα, αν οριστεί μια περιστροφή στον ώμο του παραπάνω μοντέλου τότε αυτόματα ο μετασχηματισμός αυτός θα εφαρμοστεί όχι μόνο στο βραχιόνιο οστό αλλά και σε όλο το υπόλοιπο χέρι.
Τι γίνεται, όμως, με την κίνηση των κορυφών της επιφάνειας του μοντέλου; Η ιδέα του σκελετού είναι τελείως τεχνητή και έχει ως σκοπό να υποβοηθήσει τη μοντελοποίηση της σκελετικής κίνησης. Το μοντέλο ενός ανθρωποειδούς είναι, συνήθως, ένα μοντέλο επιφάνειας που αναπαρίσταται μέσω μιας δεικτοδοτημένης λίστας εδρών όπως αυτή περιγράφηκε σε προηγούμενο κεφάλαιο. Πώς, όμως, κινείται κάθε κορυφή έτσι ώστε να ακολουθεί την κίνηση των οστών;
Εικόνα 8.6. Παράδειγμα ενός αρθρωτού αντικειμένου. Τα επιμέρους τμήματα του αντικειμένου είναι συμπαγή και μπορούν να κινηθούν γύρω από τις αρθρώσεις.
Κάθε οστό έχει το δικό του σύστημα συντεταγμένων, το οποίο συνήθως έχει ως αρχή των αξόνων τον κόμβο με τον οποίο συνδέεται με το πατρικό οστό. Ο μετασχηματισμός, λοιπόν, ο οποίος συνδέει το τοπικό σύστημα συντεταγμένων ενός οστού με το σύστημα συντεταγμένων κόσμου προκύπτει πολλαπλασιάζοντας όλους τους μετασχηματισμούς στο γράφο σκηνής οι οποίοι συνδέουν το τρέχον οστό με τη ρίζα του γράφου.
{Εξ. 8.10} |
όπου Μi ο μετασχηματισμός που μετασχηματίζει το σύστημα συντεταγμένων του κόμβου i σε αυτό του κόσμου i-1 και βρίσκεται στη διαδρομή που συνδέει τη ρίζα με τον κόμβο j. Τι γίνεται, όμως, με μια συγκεκριμένη κορυφή της επιφάνειας ενός αντικειμένου; Έστω η κορυφή v της παρακάτω εικόνας:
Εικόνα 8.7. Παράδειγμα ενός αρθρωτού αντικειμένου. Τα επιμέρους τμήματα του αντικειμένου είναι συμπαγή και μπορούν να κινηθούν γύρω από τις αρθρώσεις.
Αξίζει να σημειωθεί ότι στην παραπάνω εικόνα το οστό του αρθρωτού μοντέλου απαρτίζεται από τα δύο μαύρα διακεκομμένα ευθύγραμμα τμήματα. Η κορυφή v βρίσκεται πάνω στην επιφάνεια του χεριού, η οποία δε σχεδιάζεται για λόγους ευκολίας απεικόνισης. Μια προφανής λύση είναι η κορυφή v να ακολουθεί την κίνηση του βραχιόνιου οστού. Εφόσον, λοιπόν, οι συντεταγμένες του v έχουν οριστεί ως προς το τοπικό σύστημα συντεταγμένων, τότε η έκφραση που δίνει τις συντεταγμένες του στο σύστημα συντεταγμένων κόσμου είναι η εξής:
{Εξ. 8.11} |
Η εξάρτηση ενός σημείου μιας επιφάνειας από την κίνηση ενός μόνο οστού του αρθρωτού αντικειμένου έχει ως αποτέλεσμα αφύσικη κίνηση της επιφάνειας του αντικειμένου στις περιοχές κοντά στις αρθρώσεις, κάτι που είναι λογικό διότι η κίνηση στις περιοχές αυτές αναμένεται να επηρεάζεται από δύο τουλάχιστον οστά. Για το λόγο αυτό είναι σύνηθες να συντίθεται η κίνηση μιας κορυφής λαμβάνοντας υπόψη περισσότερα του ενός οστά και σταθμίζοντας την επίδρασή του καθενός με προϋπολογισμένα βάρη. Στην περίπτωση αυτή η θέση της κορυφής v στο σύστημα συντεταγμένων κόσμου δίνεται από την παρακάτω σχέση:
{Εξ. 8.12} |
όπου i είναι ο δείκτης και Ν ο αριθμός των οστών, από τα οποία εξαρτάται η κίνηση της κορυφής v.
Πέρα από τη σύνθεση κίνησης βάσει καρέ-κλειδιών, ιδιαίτερη κατηγορία αποτελεί και η σύνθεση δυναμικής κίνησης. Στην κατηγορία αυτή ανήκουν προσομοιώσεις, οι οποίες βασίζονται σε κανόνες που έχουν ως στόχο να προσεγγίσουν όσο καλύτερα γίνεται τους νόμους της φύσης. Στη συνέχεια παρουσιάζονται σύντομα οι βασικότερες και πιο συχνά χρησιμοποιούμενες περιπτώσεις δυναμικής σύνθεσης κίνησης.
Έστω ότι θέλουμε να συνθέσουμε την κίνηση του βλήματος ενός καταπέλτη, ο οποίος βάλλει κατά ενός τοίχου, όπως φαίνεται στην παρακάτω εικόνα.
Εικόνα 8.8. Έξι καρέ συνθετικής κίνησης ενός καταπέλτη που βάλλει προς έναν τοίχο
Το βλήμα είναι μια πέτρα, την οποία μπορούμε να θεωρήσουμε για χάρη απλότητας σφαιρική, οπότε μπορούμε να αγνοήσουμε την περιστροφική της κίνηση και να ασχοληθούμε μόνο με τη θέση της. Άρα μπορεί να προσεγγιστεί με μια σημειακή μάζα που έχει ως συντεταγμένες το κέντρο βάρους της πέτρας. Αν αγνοήσουμε την επίδραση διάφορων δυνάμεων όπως είναι η αντίσταση του ανέμου και οι μικρές διακυμάνσεις στην επιτάχυνση της βαρύτητας, στην πέτρα ασκείται μια σταθερή επιτάχυνση κατά τη διάρκεια της κίνησής της λόγω της βαρύτητας. Η κλασική μηχανική μάς δίνει απευθείας την εξίσωση της κίνησης ενός σώματος υπό την επίδραση σταθερής επιτάχυνσης:
{Εξ. 8.13} |
όπου x είναι η θέση της πέτρας, t ο χρόνος, g η σταθερή επιτάχυνση της βαρύτητας και x0, v0 η αρχική θέση και ταχύτητα του σώματος αντίστοιχα. Άρα έχουμε, πλέον, μια σχέση που συνδέει τη θέση του σώματος με το χρόνο. Τι πρέπει, όμως, τώρα να κάνουμε ώστε από αυτή τη σχέση να συνθέσουμε μια ακολουθία καρέ όπως αυτή που απεικονίζεται στην Εικόνα 8.9;
Για να συντεθεί μια τέτοια ακολουθία πρέπει αρχικά να εκτιμηθεί η χρονική ταυτότητα (timestamp) κάθε καρέ. Αυτό μπορεί να γίνει με ρουτίνες διαθέσιμες σε όλες τις γλώσσες προγραμματισμού. Στη συνέχεια, αφού υπολογιστεί η θέση του βλήματος βάσει της παραπάνω εξίσωσης, υλοποιείται ο κατάλληλος μετασχηματισμός μεταφοράς και σχεδιάζεται το καρέ.
Εικόνα 8.9. Τροχιά βλήματος που εκτοξεύεται από έναν καταπέλτη
Στην προηγούμενη παράγραφο αναλύθηκε ο τρόπος σύνθεσης της δυναμικής κίνησης στερεών σωμάτων. Τι γίνεται, όμως, όταν ένα αντικείμενο είναι παραμορφώσιμο ή ακόμα και άμορφο, όπως τα ρευστά και ο καπνός; Στην περίπτωση αυτή χρησιμοποιούνται τα λεγόμενα συστήματα σωματιδίων.
Ένα σωματίδιο θεωρείται ότι είναι μια σημειακή μάζα, η οποία κινείται υπό την επήρεια πεδίων δυνάμεων ή και μη γραμμικών αλληλεπιδράσεων με το περιβάλλον τους, όπως είναι οι συγκρούσεις με άλλα σωματίδια. Αν και η κίνηση των σωματιδίων είναι αιτιοκρατική, συνήθως δεν μπορεί να υιοθετηθεί η μεθοδολογία της προηγούμενης παραγράφου, λόγω της ύπαρξης μεγάλου αριθμού σωματιδίων αλλά και της μη γραμμικότητας που εισάγουν οι αλληλεπιδράσεις με το περιβάλλον.
Κάθε σωματίδιο ενός συστήματος σωματιδίων δεν μπορεί να απεικονιστεί ως ένα σημείο μιας και είναι αδιάστατο. Οπότε χρησιμοποιούνται διάφορες τεχνικές για την απεικόνισή τους όπως η χρήση στοιχειωδών σχημάτων (π.χ. τριγώνων, σφαιριδίων) τοποθετημένα ώστε το κέντρο βάρους τους να συμπίπτει με τη θέση του σωματιδίου.
Έστω, λοιπόν, ένα σωματίδιο στο οποίο επιδρούν διάφορες δυνάμεις, οι οποίες έχουν ως αποτέλεσμα να ασκείται πάνω του κάθε χρονική στιγμή μια γνωστή επιτάχυνση . Το πρόβλημα της προσομοίωσης του σωματιδίου αυτού ανάγεται στον υπολογισμό της θέσης του στο χρόνο, δεδομένης της επιτάχυνσης , της αρχικής ταχύτητας και της αρχικής θέσης . Είναι γνωστό, όμως, από την άλγεβρα ότι:
{Εξ. 8.14} |
Παρόμοια μπορεί να εξαχθεί η σχέση που συνδέει θέση και ταχύτητα
{Εξ. 8.15} |
Άρα συνδυάζοντας τα παραπάνω έχουμε:
{Εξ. 8.16} |
Όταν είναι δυνατός ο υπολογισμός ολοκληρώσιμης αναλυτικής μορφής της επιτάχυνσης τότε μπορεί να επιλυθεί το παραπάνω ολοκλήρωμα και απλώς να υπολογιστεί η τιμή του για κάθε χρονική στιγμή που απαιτείται από την προσομοίωση. Όπως αναφέρθηκε όμως και παραπάνω κάτι τέτοιο δεν είναι εφικτό στην πλειονότητα των περιπτώσεων, διότι ακόμα και αν μπορεί να υπολογιστεί αναλυτικά η σχέση για την επιτάχυνση, αυτή δεν είναι ολοκληρώσιμη. Για το λόγο αυτό καταφεύγουμε στην αριθμητική επίλυση της παραπάνω εξίσωσης.
Η αριθμητική ολοκλήρωση βασίζεται στο γεγονός ότι οποιαδήποτε παραγωγίσιμη συνάρτηση μπορεί να εκφραστεί ως σειρά Taylor και να υπολογιστεί έτσι η τιμή της s(t) γύρω από ένα γνωστό σημείο t0.
{Εξ. 8.17} |
Έτσι μπορούμε να έχουμε μια προσέγγιση της τιμής του s(t) εάν χρησιμοποιήσουμε έναν πεπερασμένο αριθμό από τους παραπάνω όρους. Για να κάνουμε την προσέγγιση αυτή πρέπει να γνωρίζουμε την τιμή της συνάρτησης s(t) αλλά και τις παραγώγους της, τη χρονική στιγμή t0. Η πιο απλή, πλέον, λύση είναι να πάρουμε μια προσέγγιση δύο όρων, οπότε έχουμε
{Εξ. 8.18} |
Πώς, όμως, μπορεί να εφαρμοστεί αυτή η προσέγγιση στην περίπτωση της δυναμικής προσομοίωσης; Αρκεί να σκεφτούμε ότι αυτό που επιζητούμε είναι να υπολογίσουμε τη θέση ενός αντικειμένου/σωματιδίου τη χρονική στιγμή t βάσει ενός διανύσματος κατάστασης (θέση, ταχύτητα, επιτάχυνση) των προηγούμενων χρονικών στιγμών.
Εδώ πρέπει να σημειώσουμε ότι οι προσομοιώσεις είναι διακριτές. Δηλαδή, υπολογίζονται οι φυσικές ποσότητες της προσομοίωσης τη χρονική στιγμή t και στη συνέχεια γίνονται οι κατάλληλοι υπολογισμοί για να υπολογιστούν οι ίδιες ποσότητες τη χρονική στιγμή t+1. Άρα μπορούμε να έχουμε μια έκφραση για τη θέση ως εξής:
{Εξ. 8.19} |
Ομοίως και για την ταχύτητα:
{Εξ. 8.20} |
Βάσει του δεύτερου νόμου του Νεύτωνα καταλήγουμε στην παρακάτω σχέση:
{Εξ. 8.21} |
Οι παραπάνω σχέσεις εκφράζουν την εμπρόσθια ολοκλήρωση Euler (Explicit Euler Integration) και είναι ο απλούστερος τρόπος αριθμητικής ολοκλήρωσης ενός δυναμικού συστήματος. Αυτό που κάνει πρακτικά η μέθοδος αυτή της ολοκλήρωσης είναι να υπολογίζει τις παραγώγους, δηλαδή την ταχύτητα και την επιτάχυνση, στην αρχή του διαστήματος ολοκλήρωσης [t, t+1] και να θεωρεί ότι οι παράγωγοι αυτές παραμένουν σταθερές κατά τη διάρκεια όλου του διαστήματος. Είναι προφανές ότι η προσέγγιση αυτή μπορεί να είναι ακριβής μόνο για μικρά Δt, διότι υπό την επήρεια μεγάλων επιταχύνσεων η ταχύτητα θα αλλάζει πολύ στο διάστημα αυτό, κάτι που μπορεί εύκολα να οδηγήσει σε αστάθεια.
Μια λύση είναι να εκτελεστεί ένα βήμα ολοκλήρωσης με τη μέθοδο εμπρόσθιας ολοκλήρωσης Euler και να υπολογιστούν οι παράγωγοι την επόμενη χρονική στιγμή. Στη συνέχεια επιστρέφουμε στο προηγούμενο βήμα και χρησιμοποιούμε τις παραγώγους αυτές για τη μετάβαση από τη χρονική στιγμή t στην t+1. Αυτή η μέθοδος λέγεται ημί-αντίστροφη ολοκλήρωση Euler (semi-implicit Euler) και περιγράφεται από τις παρακάτω σχέσεις.
{Εξ. 8.22} |
{Εξ. 8.23} |
όπου οι παράγωγοι της χρονικής στιγμής t+1, v(t+1), γ(t+1) υπολογίζονται από ένα προσωρινό βήμα εμπρόσθιας ολοκλήρωσης Euler.
Στις προηγούμενες παραγράφους είδαμε τρόπους να ολοκληρώνουμε και να προσομοιώνουμε ένα σύστημα όταν γνωρίζουμε για κάθε χρονική στιγμή τη θέση των αντικειμένων, την ταχύτητά τους και την επιτάχυνσή τους. Η επιτάχυνση που τους ασκείται συνδέεται άμεσα με τη δύναμη που ασκείται πάνω τους βάσει του δεύτερου νόμου του Νεύτωνα. Ακόμα πρέπει να δίνεται προσοχή ώστε να μην παραβιάζεται ο τρίτος νόμος του Νεύτωνα, που αναφέρει ότι η συνισταμένη των δυνάμεων σε ένα κλειστό σύστημα (δηλαδή, σε ένα σύστημα στο οποίο δεν ασκούνται εξωτερικές δυνάμεις) είναι μηδέν. Οπότε όταν ασκείται σε ένα σώμα Α μια δύναμη ως αποτέλεσμα της αλληλεπίδρασης με ένα άλλο σώμα Β, τότε ασκείται και στο σώμα Β ως αντίδραση ίδια και αντίθετη δύναμη.
Ποιες είναι, όμως, οι δυνάμεις που ασκούνται σε ένα αντικείμενο ή σε ένα σύστημα σωματιδίων και πώς μπορούν να μοντελοποιηθούν; Στη συνέχεια της παραγράφου αυτής παρουσιάζονται οι εκφράσεις των βασικότερων δυνάμεων που χρησιμοποιούνται στις δυναμικές προσομοιώσεις.
Βαρυτική δύναμη. Μια απλή και πολύ χρήσιμη δύναμη προκύπτει από το ομοιόμορφο βαρυτικό πεδίο:
{Εξ. 8.24} |
όπου m είναι η μάζα του αντικειμένου υπό προσομοίωση. Στην περίπτωση αυτή υποθέτουμε ότι οι διαστάσεις του προβλήματός μας σε σχέση με τον πλανήτη είναι αμελητέες, οπότε και η δύναμη έχει σταθερή κατεύθυνση. Ακόμα, εφόσον δεν εφαρμόζουμε κάποια αντίδραση στη δράση της βαρύτητας φαίνεται ότι παραβιάζουμε τον 3ο νόμο του Νεύτωνα. Αυτό δικαιολογείται, όμως, από την υπόθεση ότι οι διαστάσεις του προβλήματος (άρα και η μάζα) είναι αμελητέες σε σχέση με το μέγεθος του πλανήτη. Οπότε και η επίδραση της δύναμης αντίδρασης είναι αμελητέα. Σε περίπτωση που δεν ισχύει η παραπάνω υπόθεση μπορούμε να χρησιμοποιήσουμε την παρακάτω σχέση.
{Εξ. 8.25} |
όπου m1 και m2 είναι οι μάζες των δύο αντικειμένων που αλληλεπιδρούν, d η απόσταση μεταξύ των κέντρων βάρους τους, G η σταθερά της βαρύτητας και e το μοναδιαίο διάνυσμα που συνδέει τα κέντρα βάρους. Ο παραπάνω νόμος περιγράφει ίσες και αντίθετες δυνάμεις μεταξύ των αντικειμένων, όπου η δύναμη είναι ανάλογη στο γινόμενο των μαζών και αντιστρόφως ανάλογη του τετραγώνου της απόστασής τους.
Αεροδυναμική αντίσταση. Ο ακριβής υπολογισμός της αεροδυναμικής αντίστασης είναι ένα ιδιαίτερα πολύπλοκο πρόβλημα∙ μια προσεγγιστική λύση προκύπτει από τον παρακάτω τύπο:
{Εξ. 8.26} |
όπου ρ είναι η πυκνότητα του αέρα, cd είναι ο συντελεστής αντίστασης του αντικειμένου, α είναι η εγκάρσια επιφάνειά του και e είναι ένα μοναδιαίο διάνυσμα αντίθετο της ταχύτητας v. Όπως και στην περίπτωση της ομοιόμορφης βαρυτικής δύναμης έτσι και η παραπάνω προσέγγιση της αεροδυναμικής αντίστασης φαίνεται να παραβιάζει τον 3ο νόμο του Νεύτωνα αφού ασκείται μια δύναμη σε ένα αντικείμενο χωρίς να ασκείται η αντίθετη σε κάποιο άλλο. Ποιο είναι, όμως, το άλλο αντικείμενο; Είναι ο περιβάλλων αέρας του οποίου αλλάζει η ταχύτητα, έως ότου η κίνηση αυτή αποσβεστεί και μετατραπεί σε θερμότητα. Η διαδικασία αυτή μπορεί στις περισσότερες περιπτώσεις προσομοιώσεων γραφικών να θεωρηθεί αμελητέα, όχι όμως και σε ακριβείς προσομοιώσεις αεροδυναμικής.
Ελαστική δύναμη ελατηρίου. Μια απλή και πάρα πολύ χρήσιμη δύναμη είναι αυτή που προκύπτει από γραμμικά ιδανικά ελατήρια. Μια δύναμη ενός ελατηρίου μπορεί να περιγραφεί ως εξής
{Εξ. 8.27} |
όπου k είναι η σταθερά του ελατηρίου και x ένα διάνυσμα που περιγράφει τη μετατόπιση. Στην πράξη πολλές φορές είναι χρήσιμο να ορίσουμε ένα ελατήριο που συνδέει δύο σωματίδια και έχει ένα συγκεκριμένο φυσικό μήκος για το οποίο η δύναμη είναι μηδέν. Στην περίπτωση αυτή έχουμε:
{Εξ. 8.28} |
όπου l είναι το φυσικό μήκος του ελατηρίου και r1, r2 οι θέσεις τους. Τα ελατήρια ασκούν ίσες και αντίθετες δυνάμεις στα δύο σωματίδια καθώς υπακούουν στον 3ο νόμο του Νεύτωνα και τη διατήρηση της ορμής.
Αποσβέσεις. Μια άλλη δύναμη με ιδιαίτερο ενδιαφέρον είναι η δύναμη απόσβεσης.
{Εξ. 8.29} |
όπου kd η σταθερά απόσβεσης και v η διαφορά της ταχύτητας μεταξύ δύο σωματιδίων. Οι δυνάμεις απόσβεσης είναι ίσες και αντίθετες, οπότε διατηρούν την ορμή, αλλά αφαιρούν ενέργεια από το σύστημα. Πού πάει αυτή η ενέργεια; Σε πραγματικές αποσβέσεις, η κινητική ενέργεια μεταφέρεται σε πολύπλοκη κίνηση του ρευστού μέσα στον αποσβεστήρα και τελικά σε τυχαία σωματιδιακή κίνηση η οποία προκαλεί αύξηση της θερμότητας. Πρακτικά, βέβαια, χάνεται η κινητική ενέργεια. Οι αποσβεστήρες λειτουργούν όμοια με τα ελατήρια. Συνήθως, τα παραπάνω συνδυάζονται σε συστήματα ελατηρίου-αποσβεστήρα. Για τον υπολογισμό της δύναμης απόσβεσης, πρέπει να γνωρίζουμε την ταχύτητα σύγκλισης των δύο σωματιδίων που είναι η σχετική τους ταχύτητα κατά μήκος του άξονα που τα συνδέει.
{Εξ. 8.30} |
όπου v1 και v2 τα διανύσματα ταχύτητας των δύο σωματιδίων. Ένα άλλος τρόπος να υπολογίσουμε την ταχύτητα σύγκλισης είναι να υπολογίσουμε την απόστασή τους σε σχέση με την απόστασή τους το προηγούμενο καρέ:
{Εξ. 8.31} |
Η διαφορά είναι ότι εδώ ο υπολογισμός της παραγώγου είναι αριθμητικός, ενώ η προηγούμενη λύση ήταν ένας ακριβής αναλυτικός υπολογισμός. Η αναλυτική λύση είναι προτιμητέα για πολλούς λόγους. Πρώτα από όλα δεν απαιτεί επιπλέον χώρο αποθήκευσης. Είναι ευκολότερο να ξεκινήσουμε την προσομοίωση (δεν απαιτεί δεδομένα από το προηγούμενο καρέ), ενώ δίνει και ακριβές αποτέλεσμα αντί για προσέγγιση.
Πεδία δυνάμεων. Ένα πεδίο δυνάμεων μπορεί να οριστεί εύκολα και ανάλογα με την εφαρμογή. Για παράδειγμα, μπορεί να επιλέξουμε ένα πεδίο δυνάμεων όπου η δύναμη είναι συνάρτηση της θέσης στο πεδίο
{Εξ. 8.32} |
Ένα πεδίο δυνάμεων αναφέρεται, συνήθως, σε έναν προ-αποθηκευμένο πίνακα δυνάμεων για κάθε σημείο μιας δειγματοληψίας του χώρου, στο οποίο όταν βρεθεί ένα αντικείμενο του ασκείται η δύναμη που ανακτάται από τον πίνακα αυτόν. Ένα πεδίο δυνάμεων μπορεί να αφορά μία φυσική δύναμη όπως μαγνητισμός, βαρύτητα ή ακόμα και μηχανικές δυνάμεις όπως η αεροδυναμική αντίσταση.
Ώσεις. Μια ώση μπορεί να θεωρηθεί σαν το ολοκλήρωμα μιας δύναμης σε ένα πολύ μικρό χρονικό διάστημα, το οποίο έχει ως αποτέλεσμα πεπερασμένη μεταβολή της ορμής:
{Εξ. 8.33} |
Μια ώση συμπεριφέρεται σαν μια δύναμη, εκτός του ότι αντί να επιδρά στην επιτάχυνση, επηρεάζει απευθείας την ταχύτητα. Οι ώσεις υπακούουν τον 3ο νόμο του Νεύτωνα, οπότε τα αντικείμενα ανταλλάσσουν ίσες και αντίθετες ώσεις. Ακόμα, όπως και στις δυνάμεις, μπορούμε να υπολογίσουμε συνολική ώση ως άθροισμα διακριτών ώσεων. Οι ώσεις αποτελούν ένα ιδιαίτερα ισχυρό εργαλείο στην επίλυση των συγκρούσεων, διότι μπορούν εύκολα να περιγράψουν το αποτέλεσμα της εφαρμογής μιας πολύ ισχυρής δύναμης για ένα πολύ μικρό χρονικό διάστημα.
Όλες οι δυνάμεις που έχουμε δει μπορούν να συνδυαστούν απλά προσθέτοντάς τες. Οπότε η ολική δύναμη που ασκείται σε ένα σωματίδιο είναι το άθροισμα όλων των επιμέρους δυνάμεων. Σε κάθε καρέ υπολογίζονται όλες οι δυνάμεις του συστήματος την τρέχουσα χρονική στιγμή. Στη συνέχεια ολοκληρώνουμε το σύστημα προς το μέλλον κατά Δt, όπως ορίζει η μέθοδος αριθμητικής ολοκλήρωσης που έχουμε επιλέξει.

|
8.5. Προτεινόμενες Ασκήσεις και Προβλήματα |
|
Άσκηση 1)
Υλοποιήστε πρόγραμμα που να εκτελεί εμπρόσθια Euler ολοκλήρωση για ένα σύστημα όπου μια σφαίρα μάζας m είναι προσαρτημένη σε ένα άκρο ενός ελατηρίου φυσικού μήκους l, το οποίο κρέμεται από το ταβάνι. Τι παρατηρείτε όσον αφορά την ευστάθεια της προσομοίωσης; Ποια η επίδραση του βήματος ολοκλήρωσης;
Άσκηση 2)
Επαναλάβετε την άσκηση 1 για την περίπτωση της ημι-αντίστροφης ολοκλήρωσης Euler. Τι παρατηρείτε όσον αφορά την ευστάθεια της προσομοίωσης; Ποια η επίδραση του βήματος ολοκλήρωσης;
Άσκηση 3)
Επαναλάβετε την άσκηση 1 με σύνθεση κίνησης βάσει καρέ-κλειδιών, όπου θα υπάρχουν 4 καρέ-κλειδιά σε μια περίοδο κίνησης. Τι παρατηρείτε όσον αφορά την ευστάθεια της κίνησης; Ποια η επίδραση του βήματος ολοκλήρωσης;
Άσκηση 4)
Επαναλάβετε τις ασκήσεις 1-3 για την περίπτωση που στην παραπάνω σφαίρα είναι προσαρτημένο ακόμα ένα ελατήριο φυσικού μήκους k, στο άλλο άκρο του οποίου υπάρχει σφαίρα μάζας w. Ποια μέθοδο θα επιλέγατε στην περίπτωση αυτή; Ποια μέθοδο θα επιλέγατε αν είχαμε ένα σύστημα Ν ελατηρίων και Ν σφαιρών; |
|