 |
 |
| 4 | 'ΓΡΑΦΙΚΑ ΚΑΙ ΕΙΚΟΝΙΚΗ ΠΡΑΓΜΑΤΙΚΟΤΗΤΑ' | Μουστάκας Κ., Παλιόκας Ι., Τσακίρης Α., Τζοβάρας Δ. |
 |
 |


Πατήστε πάνω στους τίτλους των υποκεφαλαίων ή μεταφερθείτε στην αρχική σελίδα.
|
2015 |
|
ΚΕΦΑΛΑΙΟ 4: ΑΝΑΠΑΡΑΣΤΑΣΗ ΤΡΙΣΔΙΑΣΤΑΤΩΝ ΑΝΤΙΚΕΙΜΕΝΩΝ
|

|
|
ΣύνοψηΤο κεφάλαιο αυτό πραγματεύεται τρία κυρίως θέματα: το χρησιμοποιούμενο μοντέλο, τις δομές δεδομένων που χρησιμοποιούνται για την κωδικοποίηση και αποθήκευση του μοντέλου και τους αλγορίθμους που υλοποιούν την παράσταση ή άλλες αλγοριθμικές πράξεις μεταξύ μοντέλων. Έμφαση θα δοθεί στα πιο διαδεδομένα μοντέλα όπως είναι το πολυγωνικό, στις επιφάνειες Bezier που χρησιμοποιούνται ως ένθετες για να συνδέσουν άλλες επιφάνειες και τον έλεγχο του επιπέδου λεπτομέρειας των μοντέλων με το Level of Detail (LOD). Προαπαιτούμενη γνώσηΒασικές γνώσεις μαθηματικής περιγραφής διαφόρων τύπων επιφανειών. Γενικές γνώσεις σχεδίασης με βάση τον υπολογιστή (Computer Aided Design). Άνεση στην ανάγνωση κώδικα για την κατανόηση των αλγοριθμικών λύσεων που προτείνονται. |
Τα σύγχρονα συστήματα γραφικών επεξεργάζονται πολύπλοκες σκηνές με πολυάριθμα αντικείμενα τα οποία συνθέτουν την τελική εικόνα που αντιλαμβάνεται οπτικά ο χρήστης. Το πρόβλημα της αναπαράστασης αναφέρεται στον τρόπο μοντελοποίησης και δόμησης των αναπαριστώμενων αντικειμένων. Δεδομένου ότι δεν υπάρχουν ακόμη τρισδιάστατες οθόνες, ένα σύνολο από 3Δ αντικείμενα καλούνται: α. να προβληθούν πάνω σε πλεγματικές οθόνες με αποδοτικό τρόπο, β. να επιδέχονται μετασχηματισμούς και γ. να προσαρμόζονται δυναμικά στις εκάστοτε απαιτήσεις. Μέχρι σήμερα έχει προταθεί μια πληθώρα μοντέλων παράστασης 3Δ αντικειμένων ανάλογα με το είδος του αντικειμένου που αναπαριστάται και τον τρόπο που αυτό δημιουργήθηκε. Όπως θα δούμε παρακάτω, ο τρόπος δημιουργίας των μοντέλων για ποικίλα αντικείμενα του φυσικού κόσμου καθορίζεται άμεσα από το είδος της μοντελοποίησης που εξυπηρετεί καλύτερα. Για παράδειγμα, η ελεύθερη σχεδίαση με τη βοήθεια ενός προγράμματος CAD μοντελοποιεί τα αντικείμενα ως σύνολα επιφανειών, ενώ η σάρωση ενός αντικειμένου με έναν 3D scanner δημιουργεί ένα νέφος σημείων.
Τα 3Δ αντικείμενα αποτελούνται από την εσωτερική τους δομή και τις επιφάνειες που τα καλύπτουν. Κάποια είδη μοντέλων χειρίζονται αποκλειστικά και μόνο τις επιφάνειες που περικλείουν τα αντικείμενα καθώς ο χρήστης αντιλαμβάνεται οπτικά μόνο τις εξωτερικές επιφάνειες των μοντέλων και επομένως αυτές είναι που έχουν μεγαλύτερη σημασία. Όταν τα αντικείμενα έχουν οπές ή ακανόνιστα δομικά χαρακτηριστικά, τότε αυτά αποδίδονται ως επιφανειακά χαρακτηριστικά. Κατά συνέπεια το παρόν κεφάλαιο εστιάζει στα είδη των επιφανειών και στον τρόπο περιγραφής τους.
Οι καμπύλες επιφάνειες αποτελούν ουσιαστικά επέκταση των καμπυλών. Στα γραφικά οι επιφάνειες αναπαριστώνται ως πλέγματα σημείων τα οποία μπορεί να βρίσκονται πάνω σε ένα επίπεδο (δισδιάστατες επιφάνειες) ή να επεκτείνονται στις τρεις διαστάσεις. Οι επιφάνειες που μπορούν να οριστούν με μαθηματικό τρόπο, περιγράφονται σε παραμετρική ή σε μη παραμετρική μορφή. Κατά συνέπεια υπάρχουν επιφάνειες που μπορούν να οριστούν με βάση μια εξίσωση της μορφής:
{Εξ. 4.1} |
Η παραπάνω σχέση αποτελεί την μη παραμετρική αναπαράσταση ενός επιπέδου. Η παραμετρική μορφή (που είναι και η προτιμότερη) κάνει χρήση δύο μεταβλητών u και v, οι οποίες είναι απαραίτητες για την περιγραφή της επιφάνειας ως προς τους τρεις άξονες X, Y και Z:
{Εξ. 4.2} |
Διακρίνουμε δύο μεγάλες κατηγορίες επιφανειών: α. τις αναλυτικές επιφάνειες, όπως είναι για παράδειγμα οι επίπεδες επιφάνειες, οι γραμμικές επιφάνειες, οι επιφάνειες που προκύπτουν από περιστροφή επίπεδης καμπύλης, οι επιφάνειες σαρώσεως και β. οι σύνθετες επιφάνειες των οποίων η περιγραφή γίνεται με πιο πολύπλοκους τρόπους (πολυωνυμικές εξισώσεις). Στα γραφικά με υπολογιστή, οι σύνθετες επιφάνειες κατασκευάζονται από άλλες μικρότερες που ονομάζονται εμβαλωματικές επιφάνειες και επιτρέπουν την κατά τμήματα σχεδίαση και έλεγχο των επιφανειών.
Παρατηρούμε πως με σταθεροποιημένη μία από τις δύο παραμέτρους u και v, από την εξίσωση της επιφάνειας προκύπτει μία καμπύλη. Είτε σταθεροποιηθεί το u, είτε το v, θα προκύψουν καμπύλες που ανήκουν στην επιφάνεια και ονομάζονται ισοπαραμετρικές. Με σταθερό το v, προκύπτει μια καμπύλη που έχει το u ως παράμετρο και το αντίστροφο.
Έστω ότι η Ku είναι η καμπύλη της επιφάνειας σφαίρας η οποία δημιουργείται αν θέσουμε το v σταθερό και έχει εφαπτόμενο διάνυσμα το ∂S/∂u στο σημείο Α. Παρομοίως, η Kv είναι η καμπύλη που ανήκει στην επιφάνεια της σφαίρας αν θέσουμε το u σταθερό και έχει εφαπτόμενο διάνυσμα το ∂S/∂v στο ίδιο σημείο Α. Το εξωτερικό γινόμενο των δύο αυτών διανυσμάτων (∂S/∂u) x (∂S/∂v) ορίζει το κάθετο διάνυσμα της εφαπτομένης επιφάνειας στο σημείο Α, εφόσον αυτά δεν είναι συγγραμμικά. Αν για παράδειγμα η σφαίρα είναι η υδρόγειος (κατά προσέγγιση), τότε με την παραπάνω μέθοδο προκύπτουν οι ισομετρικές καμπύλες του γεωγραφικού πλάτους και μήκους. Τα εφαπτόμενα διανύσματα σε κάθε σημείο της επιφάνειας ως:
{Εξ. 4.3} |
Παρακάτω πρόκειται να αναλυθούν γνωστές κατηγορίες επιφανειών καθώς και τρόποι περιγραφής και σχεδίασής τους. Κάθε κατηγορία επιφάνειας έχει τα δικά της χαρακτηριστικά που προκύπτουν από τον τρόπο δημιουργίας και κωδικοποίησής της.
Οι επίπεδες επιφάνειες, όπως υποδηλώνει και το όνομά τους, ορίζονται με βάση ένα επίπεδο και αποτελούν τμήμα αυτού. Υπάρχουν διάφοροι τρόποι να οριστεί ένα επίπεδο, αλλά ο πιο συνηθισμένος είναι με τρία (3) μη συγγραμμικά σημεία. Εναλλακτικοί τρόποι είναι (Εικόνα 4.1) με ένα σημείο και το κάθετο σε αυτήν διάνυσμα, δύο σημεία και ένα διάνυσμα κάθετο στην επιφάνεια, ένα σημείο και δύο μη συγγραμμικά διανύσματα, και δύο σημεία Α, Β και ένα διάνυσμα μη συγγραμμικό με το ΑΒ.
Γραμμική επιφάνεια είναι αυτή που δημιουργείται από δύο καμπύλες Κ1(u) και Κ2(u) όταν ενώσουμε τα σημεία τους κατά πρόοδο της μεταβλητής u. Αν δηλαδή ενωθούν ανά δύο τα σημεία των καμπυλών που έχουν την ίδια τιμή u με ένα απλό ευθύγραμμο τμήμα, τότε το σύνολο αυτών των ευθύγραμμων τμημάτων ορίζει μια γραμμική επιφάνεια. Οπότε, ένας κύλινδρος μπορεί να προκύψει ενώνοντας ανά δύο τα σημεία δύο παράλληλων κύκλων. Έστω ένα ευθύγραμμο τμήμα που ενώνει δύο σημεία P1 και P2 και περιγράφεται από την εξίσωση:
{Εξ. 4.4} |
όπου t ∈ [0, 1].
Το ευθύγραμμο τμήμα επεκτείνεται κατά μήκος των δύο καμπυλών Κ1(u) και Κ2(u) με αποτέλεσμα να τις ενώσει σε μια επιφάνεια (Εικόνα 4.2). Αν για μια δεδομένη τιμή του u έστω um, οι δύο καμπύλες έχουν τιμές Κ1(um)=Km1 και Κ2(um)=Km2, τότε η εξίσωση της ευθείας που ενώνει τα δύο σημεία δίδεται από την εξίσωση:
{Εξ. 4.5} |
Άρα η επιφάνεια που προκύπτει από την παραπάνω ευθεία για όλα τα σημεία των δύο καμπυλών δίνεται από την ακόλουθη σχέση:
{Εξ. 4.6} |
Εικόνα 4.1. Διάφοροι τρόποι ορισμού επίπεδης επιφάνειας: Α) Με 1 σημείο και το κάθετο σε αυτό διάνυσμα, Β) 2 σημεία και 1 διάνυσμα κάθετο στην επιφάνεια, Γ) με 1 σημείο και 2 μη συγγραμμικά διανύσματα, Δ) με 2 σημεία και 1 διάνυσμα μη συγγραμμικό με το ΑΒ και ε. με 3 μη συνευθειακά σημεία
Εικόνα 4.2. Ένα παράδειγμα γραμμικής επιφάνειας ως αποτέλεσμα ένωσης δύο καμπυλών Κ1 και Κ2
Μια επιφάνεια μπορεί να προκύψει μετά από περιστροφή μιας επίπεδης καμπύλης γύρω από έναν άξονα κατά τρόπο ώστε κάθε σημείο της καμπύλης να περιτρέχει έναν κύκλο. Έστω μια καμπύλη που βρίσκεται στο επίπεδο XZ (προφίλ). Η περιστροφή της κατά 360ο γύρω από τον άξονα Ζ δημιουργεί το σχήμα που φαίνεται στην Εικόνα 4.3. Αν υποθέσουμε ότι η καμπύλη δίνεται από τη σχέση:
{Εξ. 4.7} |
Με το t ∈ (a, b) και ισχύει x2+y2=1, τότε η επιφάνεια από περιστροφή είναι ο γεωμετρικός τόπος των σημείων:
{Εξ. 4.8} |
Εικόνα 4.3. Δημιουργία επιφάνειας από περιστροφή καμπύλης

|
Σημείωση: Για τις επιφάνειες από περιστροφή ισχύει η σχέση του de Clairaut, η οποία συνδέει την απόσταση r(t) από ένα σημείο της επιφάνειας προς τον άξονα Ζ και τη γωνία θ ανάμεσα στο διάνυσμα της εφαπτομένης και τον κύκλο στο ύψος του σημείου, δηλαδή r(t)cos(θ)=const.
|
Το ευθύγραμμο τμήμα y=2x, με χ ∈ [0, 3] περιστρεφόμενο γύρω από τον άξονα y δίνεται από τον τύπο [WolframAlpha1]:
| 0<x0<3,0<θ<2π | {Εξ. 4.9} |
Ένα σχήμα δαχτυλιδιού για παράδειγμα μπορεί να σχεδιαστεί από περιστροφή γύρω από τον άξονα χ μιας καμπύλης σε σχήμα C, όπου ισχύει [WolframAlpha2]:
| , -1<x0<1 και 0<θ<2π | {Εξ. 4.10} |
H εξίσωση της επιφάνειας που προκύπτει από την περιστροφή είναι:
| , -1<x0<1 και 0<θ<2π | {Εξ. 4.11} |
Και το εμβαδό της επιφάνειας υπολογίζεται σε:
{Εξ. 4.12} |
Στην Εικόνα 4.4 φαίνονται ορισμένα παραδείγματα δημιουργίας ελλειψοειδών. Ανάλογα με τον άξονα περιστροφής προκύπτουν διαφορετικά αποτελέσματα.
Εικόνα 4.4. Επιφάνειες ελλειψοειδών από περιστροφή καμπύλης όπου η περιστροφή γίνεται: Α) ως προς τον άξονα x στο άκρο της καμπύλης, Β) ως προς τον άξονα z στο άκρο της καμπύλης, Γ) ως προς άξονα x αλλά εκτός της καμπύλης και Δ) ως προς τον άξονα z εκτός της καμπύλης.
Υπάρχουν επιφάνειες που προκύπτουν από τη μετατόπιση μιας καμπύλης ως προς μια κατεύθυνση στο χώρο Ε3 (Εικόνα 4.5). Εναλλακτικά μπορούμε να υποθέσουμε ένα ευθύγραμμο τμήμα σταθερού προσανατολισμού που ακολουθεί στο χώρο μια επίπεδη καμπύλη (τροχιά). Μια παραλλαγή αυτής της επιφάνειας είναι αυτή που προκύπτει από μετατόπιση μιας κλειστής καμπύλης κατά μήκος ενός άξονα. Τέτοιες καμπύλες είναι για παράδειγμα ένας κύλινδρος που προέκυψε από έναν κύκλο που μετακινήθηκε κατά μήκος μιας ευθείας, ή ένα τρίγωνο στο επίπεδο XY δημιουργεί ένα σφηνοειδές σχήμα μετατοπιζόμενο κατά μήκος του κάθετου άξονα Ζ.
Εικόνα 4.5. Δημιουργία επιφάνειας από μετατοπιζόμενη καμπύλη: Ένα ευθύγραμμο τμήμα ξεκινάει από το ένα άκρο της καμπύλης (πάνω-αριστερά) και διατρέχει την τροχιά που χαράζει η καμπύλη (πάνω-δεξιά) έως το άλλο άκρο της (κάτω-δεξιά) για να προκύψει μια επιφάνεια σάρωσης (κάτω-αριστερά).
Οι σύνθετες επιφάνειες είναι επιφάνειες ελεύθερης μορφής που ορίζονται από παραμετρικές εξισώσεις για να περιγράψουν τη μορφή τους. Υπάρχουν διάφορες κατηγορίες επιφανειών όπως οι δικυβικές επιφάνειες Hermite, οι NURBS για ομαλότερες επιφάνειες, οι επιφάνειες Coons και Bezier. Στο κεφάλαιο αυτό θα ασχοληθούμε περισσότερο με τις επιφάνειες Bezier που είναι πολύ διαδεδομένες στο σχεδιασμό επιφανειών, την τμηματοποίηση και ένωση επιφανειών.
Οι καμπύλες Bezier (που εξετάσαμε σε προηγούμενο κεφάλαιο) μπορούν να γενικευθούν για να περιγράψουν παραμετρικές επιφάνειες. Με αντικατάσταση κάθε σημείου της καμπύλης Bezier βαθμού m με μια νέα διαφορετική καμπύλη Bezier βαθμού n προκύπτει η επιφάνεια:
{Εξ. 4.13} |
όπου:
{Εξ. 4.14} |
είναι ένα πολυώνυμο Μπέρνσταϊν (Bernstein Polynomial) και (n¦i)= n!/i!(n-i)! είναι ο διωνυμικός συντελεστής.
Η προηγούμενη σχέση περιγράφει μια καμπύλη Bezier που ξεκινάει με την τιμή 0 για το t και ολοκληρώνεται για t=1. Καθώς οι επιφάνειες Bezier αποτελούν ουσιαστικά επέκταση των καμπυλών Bezier από τις δύο διαστάσεις στις τρεις, οι επιφάνειες που προκύπτουν κληρονομούν αρκετές από τις ιδιότητες των καμπυλών Bezier. Για παράδειγμα, το στερεό ελάχιστου όγκου που περιλαμβάνει τα σημεία ελέγχου μια καμπύλης Bezier περιλαμβάνει και την ίδια την καμπύλη, επειδή ισχύει:
{Εξ. 4.15} |
Το m δίνει το βαθμό της καμπύλης Bezier προς την κατεύθυνση του u και το ν το βαθμό προς την κατεύθυνση του v. Όπως οι καμπύλες Bezier, έτσι και οι επιφάνειες ορίζονται με μοναδικό τρόπο, με βάση τα (u+1)(v+1) σημεία ελέγχου. Το σύνολο των σημείων ελέγχου ορίζει το πολύεδρο ελέγχου. Τα σημεία ελέγχου καθορίζουν την καμπυλότητα κατά μήκος της κάθε καμπύλης. Όπως ισχύει στις καμπύλες Bezier, έτσι και στις αντίστοιχες επιφάνειες υπάρχει παρεμβολή στα ακραία σημεία ελέγχου, ενώ οι επιφάνειες κατά κανόνα δε διέρχονται από τα ενδιάμεσα σημεία ελέγχου, αλλά το σχήμα της επιφάνειας ‘έλκεται’ από αυτά στις περιοχές προσέγγισης (Εικόνα 4.6). Όπως η περίπτωση των συνευθειακών σημείων ελέγχου υποβιβάζει μια καμπύλη Bezier σε ευθύγραμμο τμήμα, έτσι και η περίπτωση των συνεπίπεδων σημείων ελέγχου υποβιβάζει μια καμπύλη Bezier σε επίπεδη επιφάνεια.
Η μετακίνηση ενός σημείου ελέγχου δύναται να επηρεάσει όχι μόνο τη γειτονιά του σημείου ελέγχου, αλλά και την ευρύτερη περιοχή της επιφάνειας. Αυτό εισάγει κάποιες δυσκολίες στην επεξεργασία των επιφανειών Bezier με λογισμικό CAD και η λύση που συνήθως εφαρμόζεται είναι η απομόνωση της περιοχής παρέμβασης από την υπόλοιπη επιφάνεια με διαίρεση της επιφάνειας (εμβαλωματικές επιφάνειες, όπως θα δούμε παρακάτω).
Παρατηρούμε ότι για σταθεροποιημένη μία εκ των δύο μεταβλητών u και v, αν εφαρμόσουμε τις ακρότατες τιμές τους και επιπλέον κρατήσουμε μόνο τις τιμές 0 και 1 για το t, τότε οι ισοπαραμετρικές καμπύλες της επιφάνειας περιορίζονται στις συνοριακές καμπύλες. Επίσης, από οποιαδήποτε συνοριακή καμπύλη κι αν ξεκινήσει η σχεδίαση, το αποτέλεσμα θα είναι το ίδιο κατά ομοιότητα με τη συμμετρία στη σχεδίαση καμπυλών Bezier (ανάγνωση των σημείων ελέγχου με αντίστροφη σειρά).
Επειδή τα σημεία ελέγχου μιας σύνθετης επιφάνειας είναι περισσότερα από ό,τι μπορεί να επεξεργαστεί ένας χρήστης συστήματος CAD, οι καμπύλες αναφοράς ορίζονται ως καμπύλες που επεξεργάζεται ο χρήστης για να μεταδώσει μια επιθυμητή γεωμετρική αλλαγή στην επιφάνεια Bezier. Καμπύλες αναφοράς μπορούν να είναι οι συνοριακές καμπύλες ή καμπύλες που επιλέγονται από το σύστημα ή από τον ίδιο τον χρήστη.
Παρά τις ενδιαφέρουσες ιδιότητες των καμπυλών Bezier, υπάρχουν και ορισμένα μειονεκτήματα από τη χρήση τους στα συστήματα γραφικών. Το κυριότερο είναι ότι αυξάνεται πολύ η πολυπλοκότητά τους όταν έχουμε πολυπληθή σύνολα σημείων ελέγχου.
Εικόνα 4.6. Επιφάνεια Bezier σε κατάσταση σχεδίασης όπου με μαύρο χρώμα φαίνονται οι συνοριακές καμπύλες και με κόκκινο χρώμα φαίνονται τα ακραία σημεία ελέγχου (SketchUp 2015)
Για μια επιφάνεια Bezier, οι μεγάλες τιμές του n και του m, όπως είναι φυσικό, αυξάνουν σε μεγάλο βαθμό την πολυπλοκότητα της επιφάνειας και ταυτόχρονα το υπολογιστικό κόστος και την κατανάλωση πόρων στο σύστημα γραφικών. Για την αποδοτική περιγραφή των επιφανειών Bezier, η ενδεδειγμένη λύση είναι ο σχεδιασμός και η συνένωση μικρότερων επιφανειών με τη χρήση του αλγορίθμου deCasteljau. Μπορεί μάλιστα να εφαρμοστεί περιορισμός του βαθμού σε κυβικές επιφάνειες Bezier για τον έλεγχο της πολυπλοκότητας.
Γενικά δεν απαιτείται ο βαθμός της επιφάνειας για καθεμία από τις δύο διευθύνσεις να είναι ο ίδιος. Άμεση συνέπεια αυτού είναι ότι δεν απαιτείται, η διαίρεση να γίνει σε επιφάνειες με ίσο αριθμό σημείων ελέγχου. Επειδή, όμως, μας ενδιαφέρει η κατάτμηση σε επιφάνειες του ίδιου βαθμού, τότε γίνεται ανύψωση του βαθμού προς τη μία ή και τις δύο κατευθύνσεις. Η κατάτμηση μιας επιφάνειας ξεκινάει από την κατάτμηση των καμπυλών που την απαρτίζουν. Έστω η καμπύλη Bezier που δίνεται από το πολυώνυμο:
{Εξ. 4.16} |
Όπου bi,n είναι τα πολυώνυμα Bernstein. Η καμπύλη αυτή διαιρείται στις καμπύλες:
{Εξ. 4.17} |
και
{Εξ. 4.18} |
Εφαρμόζοντας την παραπάνω κατάτμηση για ένα σημείο P(u,v) που ανήκει σε μια επιφάνεια Bezier, ο αλγόριθμος ξεκινάει για καθεμία θέση του u, έστω αρχικά τη μηδενική, να υπολογίζει τα n+1 σημεία ελέγχου που αντιστοιχούν στην καμπύλη προς την κατεύθυνση του v σε αυτή τη θέση. Αυτά ορίζουν την ισοπαραμετρική καμπύλη στη θέση της τρέχουσας τιμής του u. Το σημείο P(u,v) που αναζητάμε είναι σημείο αυτής της καμπύλης. Για να προσδιορίσουμε συγκεκριμένα ποιο σημείο είναι, θα χρειαστεί να εφαρμόσουμε ξανά τον αλγόριθμο deCasteljau, αυτή τη φορά για τη δεδομένη τιμή του v. Η δεύτερη επανάληψη του αλγορίθμου παίρνει ως είσοδο την ισοπαραμετρική καμπύλη που προέκυψε από το πρώτο βήμα και λύνει ως τη ζητούμενη τιμή του v.
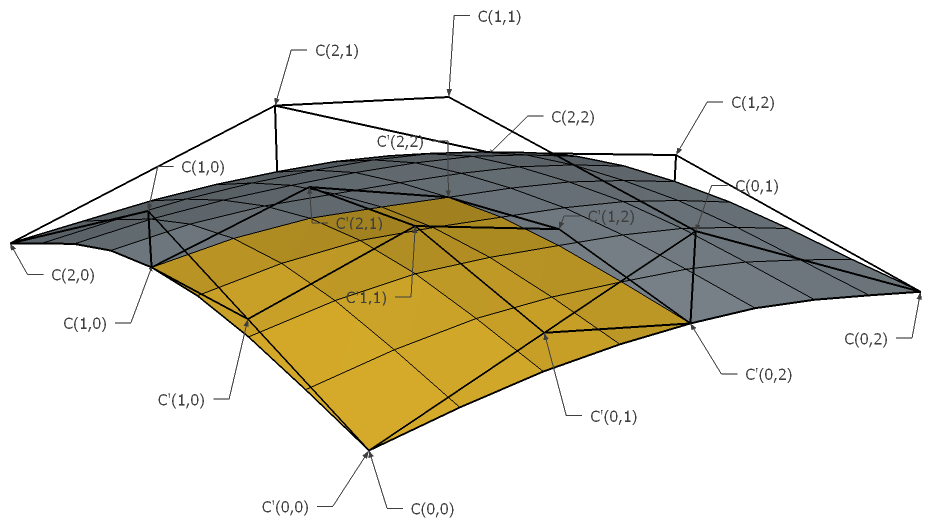
Ο αλγόριθμος deCasteljau έχει διπλή χρησιμότητα: α. χρησιμοποιείται στο σχεδιασμό επιφανειών Bezier και β. βρίσκει εφαρμογή στην κατάτμηση επιφανειών. Έστω ότι η διαίρεση μια επιφάνειας Bezier με το δισδιάστατο ανάλογο του αλγορίθμου deCasteljau γίνεται σε ένα σημείο P(u0,v0). Αυτό το σημείο διαιρεί την κάθε καμπύλη Bezier στην οποία ανήκει σε δύο μέρη, άρα την επιφάνεια σε τέσσερις (4) επιμέρους επιφάνειες του ίδιου τύπου. Έτσι προκύπτουν τέσσερα σύνολα από σημεία ελέγχου Α,Β,Γ,Δ (Πίνακας 4.1). Αν η επιφάνεια είναι βαθμού mxn, τότε από τα (m+1)(n+1) σημεία ελέγχου της θα προκύψουν τέσσερις ομάδες σημείων ελέγχου (Πίνακας 4.1). Η υλοποίηση του αλγορίθμου deCasteljau για επιφάνειες Bezier προκύπτει από τον αντίστοιχο αλγόριθμο που χρησιμοποιείται στις καμπύλες και γενικεύεται έτσι ώστε να μπορεί να χειρίζεται επιφάνειες (Λίστα 4.1) [Θεοχάρης και άλλοι, 2010].
1. point bezierPointSurface (int m, int n, float u, float v; point controlPoints[][]);
2. {
3. point tempPoint[n+1];
4. point curvePoint[n+1];
5.
6. for (i=0; i<=m; i++)
7. {
8. for (j=0; j<=n; j++)
9. {
10. tempPoint[j]=controlPoints[i][j];
11. }
12. curvePoint[i]=bezierPoint(n, tempPoint, v);
13. }
14. return bezierPoint(n, curvePoint, u);
15. }
Λίστα 4.1. Ψευδοκώδικας του αλγορίθμου de Casteljau για επιφάνειες Bezier
Πίνακας 4.1. Παράδειγμα επιφάνειας Bezier βαθμού 2x2 που χωρίστηκε σε 4 επιφάνειες ίδιου τύπου με τη βοήθεια του αλγορίθμου de Casteljau
| Περιοχές Επιφανειών | Επιφάνεια | Σημεία Ελέγχου |
|---|---|---|
|
Α | (m'+1)(n'+1) |
| B | (m'+1)(n'+1) | |
| Γ | (m'+1)(n'+1) | |
| Δ | (m'+1)(n'+1) | |
| Συνολική επιφάνεια | (m+1)(n+1) | |
| όπου
(m'+1)(n'+1) |
||
Ο χειρισμός επιφανειών απαιτεί μεταξύ άλλων οι επιφάνειες που σχεδιάζονται να μπορούν να ενωθούν μεταξύ τους. Μια επιφάνεια που παρεμβάλλεται ανάμεσα σε δύο ή περισσότερες άλλες για να δημιουργήσει μια συνεχή μεγαλύτερη επιφάνεια ονομάζεται εμβαλωματική επιφάνεια (patch surface). Στη συνέχεια θα εξετάσουμε μια διαδεδομένη λύση που χρησιμοποιεί δικυβικές επιφάνειες Bezier. Ένα εμβάλωμα Bezier είναι μια παραμετρική επιφάνεια αποτελείται από ένα πλέγμα 4x4 και ορίζεται με βάση ένα σύνολο από 16 σημεία ελέγχου. Στην Εικόνα 4.7 παρατίθεται ένα παράδειγμα κυβικής εμβαλωματικής επιφάνειας Bezier με m=n=3.
Όπως και στις επιφάνειες Bezier πιο γενικής μορφής που έχουν εξεταστεί μέχρι τώρα, έτσι στις εμβαλωματικές επιφάνειες δε χρειάζεται να αποθηκεύονται οι συντεταγμένες των σημείων γραμμικής παρεμβολής, αλλά μόνο των σημείων ελέγχου. Η χρήση των εμβαλωμάτων Bezier προσφέρει το πλεονέκτημα της αναλυτικής περιγραφής της επιφάνειας, του εύκολου χειρισμού και των καλύτερων συνθηκών συνέχειας στα σημεία 'συγκόλλησης' σε σχέση με άλλες εμβαλωματικές επιφάνειες χαμηλότερης τάξης, όπως τα τρίγωνα Bezier ή οι διτετραγωγικές μορφές.
Εικόνα 4.7. Εμβαλωματική δικυβική επιφάνεια Bezier: υπολογίζονται οι καμπύλες Bezier προς την κατεύθυνση u με σταθερό v (κόκκινη γραμμή) και το αντίστροφο (πράσινη γραμμή).
Από την άλλη πλευρά, είναι πιο δύσκολος ο υπολογισμός τομών με γραμμές καθιστώντας δύσκολη την άμεση εφαρμογή τεχνικών, όπως η παρακολούθηση ακτίνας (ray tracing) και των αλγόριθμων προοπτικής προβολής (perspective projection). Μια λύση στα παραπάνω προβλήματα είναι η περαιτέρω διαίρεση των εμβαλωματικών επιφανειών σε τρίγωνα (τριγωνοποίηση). Υπό μορφή πίνακα, οι εμβαλωματικές επιφάνειες Bezier μπορούν να παρασταθούν ως:
Υπό μορφή πίνακα, οι εμβαλωματικές επιφάνειες Bezier μπορούν να παρασταθούν ως:
{Εξ. 4.19} |
όπου:
Cx = BTGxB
Cy = BTGyB
Cz = BTGzB
και
Η παράσταση των τρισδιάστατων αντικειμένων στα γραφικά έχει σκοπό την όσο το δυνατόν πιο πιστή οπτική απόδοση των αντικειμένων (πιστότητα ή ρεαλιστικότητα της αναπαράστασης), συνήθως του φυσικού κόσμου. Ταυτόχρονα μας ενδιαφέρει αυτά τα μοντέλα να επιδέχονται εύκολα πράξεις γεωμετρικής και αλγοριθμικής επεξεργασίας (επεξεργασιμότητα). Για το σκοπό της αναπαράστασης λοιπόν, έχουν αναπτυχθεί διάφορα μοντέλα που μπορούν να χειριστούν 3Δ αντικείμενα ανεξάρτητα από τη διαθέσιμη ποσότητα πληροφορίας (ανεξαρτησία από όγκο πληροφοριών). Άλλα κριτήρια επιλογής μοντέλων είναι η συγκρατημένη κατανάλωση πόρων μνήμης (εξοικονόμηση χώρου) και η υψηλή ταχύτητα επεξεργασίας τους (αποδοτικότητα) από τους ανάλογους αλγορίθμους.
Είναι γνωστό ότι η ακρίβεια και η υψηλή πιστότητα στην αναπαράσταση προϋποθέτει μεγάλη ποσότητα πληροφορίας. Τα μοντέλα που προτιμώνται στις συνήθεις περιπτώσεις είναι αυτά που με την ελάχιστη δυνατή πληροφορία επιτυγχάνουν ικανοποιητική πιστότητα αναπαράστασης. Ωστόσο, δεν είναι δυνατόν πάντοτε να προσδιοριστεί με ακρίβεια το επίπεδο λεπτομέρειας που απαιτείται ώστε να περιγραφεί ικανοποιητικά κάθε μοντέλο. Για αυτό το λόγο οι δημιουργοί ή οι υπεύθυνοι περιεχομένου φροντίζουν να διατηρούν στις συλλογές τους τα αρχικά αντίγραφα των μοντέλων που χρησιμοποιούν στη μέγιστη δυνατή λεπτομέρεια που είναι αυτά διαθέσιμα. Για κάθε επιμέρους χρήση δημιουργούν ένα αντίγραφο συνήθως μικρότερης πολυπλοκότητας (ποσότητας πληροφορίας), δηλαδή ένα απλοποιημένο αντίγραφο. Άρα στα παραπάνω κριτήρια επιλογής μοντέλων μπορούμε να προσθέσουμε ικανότητα να επιδέχονται απλοποίηση.
Στο σημείο αυτό μπορούμε να διακρίνουμε δύο μεγάλες οικογένειες μοντελοποίησης και παράστασης (Εικόνα 4.8). Η πρώτη είναι ικανή να χειρίζεται σύνολα επιφανειών (Boundary Representation-BREP), ενώ η δεύτερη χειρίζεται όγκους αντικειμένων (solids). Καθεμία παρουσιάζει ορισμένα πλεονεκτήματα και μειονεκτήματα. Στη μοντελοποίηση επιφανειών για παράδειγμα έχουμε βέβαια κέρδος στην κατανάλωση υπολογιστικής ισχύος, αλλά αδυναμία αναπαράστασης ημιδιάφανων αντικειμένων. Σε μια εφαρμογή ψηφιακού ιατρικού Άτλαντα για παράδειγμα, το εσωτερικό ενός μοντέλου ανθρωπίνου οργάνου ενδιαφέρει εξίσου όσο και η επιφάνειά του.
Εικόνα 4.8. Στα μοντέλα αναπαράστασης επιφανειών, ένας κύβος αναπαρίσταται από τις 6 έδρες του (αριστερά), ενώ η αφαίρεση μίας από αυτές καθιστά αυτομάτως ορατό το εσωτερικό του (δεξιά)
Από την άλλη μεριά, στη μοντελοποίηση όγκων απαιτείται η κατανάλωση συγκριτικά περισσότερων πόρων του συστήματος σε σχέση με τη μοντελοποίηση επιφανειών. Πέρα από αυτό, υπάρχει δυσκολία παράστασης μη κλειστών αντικειμένων ή αντικειμένων που μας ενδιαφέρει μόνο η αναπαράσταση της εξωτερικής τους επιφάνειας, όπως είναι για παράδειγμα το κέλυφος της Γης, ή η επιφάνεια του νερού.
Τα μοντέλα επιφανείας, είτε βασίζονται στη μαθηματική περιγραφή των αναπαριστώμενων αντικειμένων όπως είναι οι επιφάνειες Bezier και οι παραμετρικές επιφάνειες, είτε εξειδικεύονται στο Πολυγωνικό Μοντέλο στο οποίο κατά κανόνα τα αναπαριστώμενα αντικείμενα δεν έχουν μαθηματική περιγραφή και αναπαρίστανται προσεγγιστικά. Τα μοντέλα που βασίζονται στις μαθηματικές περιγραφές των επιφανειών παρουσιάζουν μεγαλύτερη ακρίβεια στην αναπαράσταση και επιτυγχάνουν ακριβέστερους υπολογισμούς, αλλά δεν μπορούν να περιγράψουν πολύπλοκα αντικείμενα με τυχαία σχήματα και οργανικές μορφές όπως τα συνήθη αντικείμενα του φυσικού κόσμου.
Το Πολυγωνικό μοντέλο είναι το διαδεδομένο μοντέλο παράστασης επιφανειών. Σύμφωνα με αυτό, μια σύνθετη επιφάνεια αποτελείται από έναν μεγάλο αριθμό από τετράπλευρα ή τρίγωνα που ενώνουν ένα πλήθος κορυφών. Δηλαδή το πολύγωνο ή το τρίγωνο -που είναι η πιο απλή εκδοχή του- αποτελούν την ελάχιστη ποσότητα πληροφορίας που μπορεί να περιέχει το μοντέλο αναπαράστασης, ανεξάρτητα φυσικά από το εμβαδόν της επιφάνειας. Στην Εικόνα 4.9, φαίνεται ένα μοντέλο αυτοκινήτου με έντονες καμπύλες (σκαραβαίου) σε τρεις διαφορετικές ποιότητες που καθορίζονται από το συνολικό αριθμό πολυγώνων.
Εικόνα 4.9. Ένα πολυγωνικό μοντέλο αυτοκινήτου με: α) 39000 επιφάνειες (αριστερά), 9000 επιφάνειες (στο μέσον) και 1000 επιφάνειες (δεξιά)

|
Σημείωση: Υπάρχουν διάφοροι μορφότυποι για την αποθήκευση πολυγωνικών μοντέλων. Μερικοί από τους πιο δημοφιλείς είναι το 3ds (3D Studio Max), το dxf και το dwg (AutoCAD), το dae που υποστηρίζεται από το Google SketchUp και το obj που είναι ένα ανοιχτό πρότυπο ποικίλης χρήσης για 3Δ αντικείμενα.
|
Η τριγωνοποίηση των αναπαριστώμενων επιφανειών είναι προτιμότερη καθώς εμφανίζει ορισμένα πλεονεκτήματα. Τρία σημεία που ορίζουν ένα τρίγωνο είναι πάντοτε συνεπίπεδα, άρα το τριγωνικό μοντέλο παράγεται από οποιοδήποτε ανωτέρου επιπέδου μοντέλο που βασίζεται σε πολύγωνα. Επιπρόσθετα, τα μοντέλα που βασίζονται σε τριγωνικές στοιχειώδεις επιφάνειες είναι πιο φιλικά προς τους αλγορίθμους που χρησιμοποιούν γραμμές σάρωσης (scanline rendering) και ορισμένους αλγορίθμους φωτισμού (Phong Shading), όπως θα δούμε σε παρακάτω κεφάλαιο.
Μια εύλογη ερώτηση που προκύπτει είναι: πόσα τρίγωνα άραγε απαιτούνται για μια καλή προσέγγιση; Πόσο μπορεί να μειωθεί η πληροφορία που εμπεριέχεται στο μοντέλο έτσι ώστε να μη μειωθεί σημαντικά η ποιότητα της παράστασης; Δεν υπάρχει μια μονοσήμαντη απάντηση στο παραπάνω ερώτημα. Μια κοίλη επιφάνεια απαιτεί μεγαλύτερο αριθμό πολυγώνων (ή τριγώνων) από μια επίπεδη επιφάνεια. Ένα αντικείμενο που προβάλλεται κατά τρόπο που να καταλαμβάνει μεγάλο ποσοστό της προβολικής επιφάνειας (π.χ. οθόνη υπολογιστή) απαιτεί μεγαλύτερο αριθμό πολυγώνων από ένα άλλο αντικείμενο που εμφανίζεται μικρό (ή πολύ μακρινό) σε σχέση με την απόσταση παρατήρησης.
Επίσης, μέρος της πολυπλοκότητας των αντικειμένων αναπαρίσταται και από την υφή της επιφάνειάς τους και όχι μόνο από την κυρτότητα της ίδιας της επιφάνειας. Η επιφάνεια μιας ηλεκτρονικής πλακέτας για παράδειγμα, μπορεί να προσεγγιστεί ικανοποιητικά από μια απλή ορθογωνική επιφάνεια που επενδύεται από μια εικόνα η οποία αναπαριστά τα λεπτομερή στοιχεία του ηλεκτρονικού κυκλώματος.
Η ψηφιοποίηση αντικειμένων του φυσικού κόσμου μπορεί να πραγματοποιηθεί με τη χρήση ειδικών συσκευών που ονομάζονται 3Δ Ψηφιοποιητές. Η αρχή λειτουργίας τους είναι η μέτρηση ακριβείας με τη βοήθεια μιας ακτίνας λέιζερ που εκπέμπεται προς ένα περιστρεφόμενο αντικείμενο. Το προς ψηφιοποίηση αντικείμενο τοποθετείται πάνω σε περιστρεφόμενο δίσκο στη βάση της συσκευής, ενώ ο μετρητής απόστασης, κινούμενος και αυτός ως προς τον κάθετο άξονα, υπολογίζει με υψηλή συχνότητα (σε μικρά χρονικά διαστήματα) την απόσταση προς την επιφάνεια του αντικειμένου καθώς αυτή κινείται κυκλικά. Ανάλογα με τον τύπο της συσκευής ψηφιοποίησης, το αντικείμενο που μας ενδιαφέρει μπορεί να παραμένει σταθερό και να κινείται ο αισθητήρας.
Κάθε μέτρηση αντιστοιχεί σε ένα σημείο πλέγματος που έχει συγκεκριμένες συντεταγμένες και χρώμα. Το λογισμικό της συσκευής συνδέει ανά ζεύγη τα σημεία του πλέγματος για να σχηματίσει ακμές και στη συνέχεια επιφάνειες προσεγγίζοντας την εξωτερική επιφάνεια του αντικειμένου. Δύο προφανή μειονεκτήματα του τρισδιάστατου ψηφιοποιητή είναι πρώτον ότι μπορεί να ψηφιοποιήσει μόνο κυρτά αντικείμενα και δεύτερον ότι η χρήση του περιορίζεται σε αντικείμενα αρκετά μικρά σε μέγεθος προκειμένου να χωρέσουν στη συσκευή. Το τελευταίο πρόβλημα είναι και το πιο εύκολα επιλύσιμο καθώς υπάρχουν πλέον σαρωτές ανοιχτού τύπου, όπως ο σαρωτής χειρός που φαίνεται στην Εικόνα 4.10.
Άλλα προβλήματα που σχετίζονται με την κυματική φύση της τεχνολογίας των 3Δ σαρωτών έχουν να κάνουν με την αδυναμία αναπαράστασης ανακλαστικών επιφανειών (π.χ. λείων επιφανειών), διάφανων αντικειμένων ή επιφανειών που σκιάζονται από άλλες. Είναι συνηθισμένο ένα αντικείμενο να πρέπει να σαρωθεί δεκάδες ή εκατοντάδες φορές από διαφορετικές οπτικές γωνίες για να δημιουργηθεί ένα μοντέλο καλής ποιότητας. Η ακτινοβολία που χρησιμοποιούν οι 3Δ σαρωτές είναι ηλεκτρομαγνητικής φύσης (φως ενός φάσματος συχνοτήτων), ακτίνες Χ, ή υπέρηχοι.
Εικόνα 4.10. Laser σαρωτής χειρός για τη δημιουργία 3Δ μοντέλου [Πηγή: flickr, Creative Tools , CC BY 2.0]
Το ανάγλυφο της επιφάνειας προκύπτει υπολογίζοντας με μεγάλη ακρίβεια την απόσταση από την πηγή της ακτινοβολίας έως την προσπίπτουσα επιφάνεια. Με γνωστή την ταχύτητα του φωτός C, οι σαρωτές παλμού φωτός (time-of-flight scanners) υπολογίζουν το χρόνο t που χρειάζεται η φωτεινή δέσμη να φτάσει στην επιφάνεια και να ανακλαστεί πίσω, άρα να διανύσει δύο φορές την απόσταση από την πηγή προς την επιφάνεια. Η απόσταση αυτή είναι C*t/2, ενώ η ακρίβεια στη μέτρηση της απόστασης είναι ανάλογη της ακρίβειας στη μέτρηση του χρόνου. Μια παραλλαγή αυτής της μεθόδου χρησιμοποιεί μέτρηση της διαφοράς φάσης ανάμεσα στη φωτεινή ακτίνα που στέλνεται προς το αντικείμενο και αυτής που ανιχνεύεται ως επιστροφή για να επιτύχει ακόμη μεγαλύτερη ακρίβεια στη μέτρηση.
Υπάρχουν και απτικοί σαρωτές που χρησιμοποιούν την επαφή ενός κινούμενου άκρου με την επιφάνεια του αντικειμένου έτσι ώστε να δημιουργήσουν το πλέγμα των σημείων που απαιτείται για την ψηφιοποίηση. Το κυριότερο πρόβλημα είναι ότι η επαφή με το αντικείμενο μπορεί να προκαλέσει φθορές ή να αλλοιώσει τις μετρήσεις. Σε συνδυασμό με το γεγονός ότι η σάρωση γίνεται χειροκίνητα καθιστά την όλη διαδικασία πολύ αργή και κουραστική σε σχέση με τους οπτικούς σαρωτές, γι’ αυτό το λόγο οι απτικοί σαρωτές δεν είναι τόσο διαδεδομένοι.
Το γνωστό εικονοστοιχείο (pixel) αναφέρεται σε μια περιοχή της πλεγματικής οθόνης για να προσδιορίσει τη μικρότερη δυνατή επιφάνεια που διαθέτει ιδιότητες θέσης και χρωματισμού. Αντιστοίχως ορίζεται το σημειακό στοιχείο επιφάνειας που στη διεθνή ορολογία αναφέρεται ως surfel (Surface Element) και προσδιορίζει μια μικρή περιοχή επιφάνειας. Η στοιχειώδης αυτή επιφάνεια είναι τμήμα του φλοιού του αναπαριστώμενου αντικειμένου και είναι πάντοτε προσανατολισμένη προς το χρήστη. Στο χειρισμό στερεών και κλειστών επιφανειών θα ήταν πιο βολικό ένα μοντέλο διαίρεσης όγκου έτσι ώστε κάθε αντικείμενο να καταλαμβάνει συγκεκριμένο αριθμό στοιχειωδών μονάδων όγκου.
Πράγματι, υπάρχει ένα κβάντο χώρου που διαιρεί το χώρο σε στοιχειώδη σωματίδια για τα οποία αποδεχόμαστε ότι δε διασπώνται σε μεγαλύτερο βαθμό. Έτσι, η μικρότερη ποσότητα όγκου στα γραφικά ορίζεται με το voxel (volume+element), το οποίο στην Ελληνική αποδίδεται με το νεολογισμό Ογκοστοιχείο. Αποτελεί ένα χρήσιμο εργαλείο για τον ογκομετρικό χειρισμό στερών και χρησιμοποιείται πολύ στην οπτικοποίηση επιστημονικών και ιατρικών δεδομένων. Επίσης, χρησιμοποιείται συστηματικά στο χώρο των βιντεοπαιχνιδιών γιατί αναπαριστά καλύτερα το έδαφος (terrain) και διάφορα χαρακτηριστικά του όπως οι γέφυρες και οι σπηλιές. Στην Εικόνα 4.11, φαίνεται ένα παράδειγμα μετατροπής ενός αντικειμένου από το πολυγωνικό μοντέλο στο μοντέλο υποδιαίρεσης χώρου με ογκοστοιχεία. Το μέγεθος του ογκοστοιχείου δημιουργεί διαφορετικές ποιότητες (ή αναλύσεις), όταν μεταβάλλεται.
Εικόνα 4.11. Διαίρεση ενός αντικειμένου σε ογκοστοιχεία (voxels) σε 3 διαφορετικές αναλύσεις με τη χρήση του binvox [Nooruddin & Turk, 2003]: κύβος 1024 ογκοστοιχείων (αριστερά), 512 ογκοστοιχείων (κέντρο) και 256 ογκοστοιχείων (δεξιά)
Ένα voxel αναπαριστά ένα σημείο σε ένα τρισδιάστατο πλέγμα και όχι έναν όγκο στον R3 χώρο. Όταν επιπρόσθετα μας ενδιαφέρει και η περιγραφή της δυναμικής συμπεριφοράς ενός χώρου που καταλαμβάνεται από m x n x k voxels για ένα χρονικό διάστημα έστω t στιγμών, τότε ο 4Δ χώρος των δεδομένων που προκύπτει μπορεί να περιγραφεί με το γενικότερο όρο doxel (dynamic voxel). Στην περίπτωση αυτή χρειαζόμαστε ένα αποθηκευτικό σύστημα για m x n x k x t doxels.
Ας παραμείνουμε, όμως, στο απλό ογκοστοιχείο και ας το θεωρήσουμε το ‘3Δ εικονοστοιχείο’ που θα μας βοηθήσει να παραστήσουμε στερεά αντικείμενα, όπως περίπου συμβαίνει με τα τουβλάκια LEGO. Οι αλγόριθμοι ‘voxelization’, δηλαδή σχεδίασης με ογκοστοιχεία σε τρεις διαστάσεις χρησιμοποιούν τις μεθόδους σχεδίασης εικονοστοιχείων κατά παρόμοιο τρόπο με τον αλγόριθμο του Bresenham, αλλά γενικευμένες στον R3 χώρο. Ορισμένες ενέργειες που πρέπει να λαμβάνουν υπόψη και τα γειτονικά ογκοστοιχεία, όπως για παράδειγμα η ‘γέμιση’ μιας κλειστής περιοχής με ογκοστοιχεία, θεωρούν γύρω από κάθε ογκοστοιχείο μια γειτονιά 26 ογκοστοιχείων (Εικόνα 4.12). Παρόμοια με την polygonFill που χρησιμοποιείται για το χρωματισμό πολυγώνων στις δύο διαστάσεις θεωρώντας μια γειτονιά 4 ή 8 εικονοστοιχείων, η fillVolume (Λίστα 4.2) γεμίζει μια κλειστή περιοχή ξεκινώντας από ένα εσωτερικό σημείο και ελέγχοντας τα γειτονικά μέχρι να φτάσει στα όρια της περιοχής γεμίσματος.
Εικόνα 4.12. Διαίρεση ενός αντικειμένου σε ογκοστοιχεία (voxels) σε 3 διαφορετικές αναλύσεις με τη χρήση του binvox [Nooruddin & Turk, 2003]: κύβος 1024 ογκοστοιχείων (αριστερά), 512 ογκοστοιχείων (κέντρο) και 256 ογκοστοιχείων (δεξιά)

|
Σημείωση: Μια εφαρμογή που κάνει εκτεταμένη χρήση της υποδιαίρεσης χώρου με ογκοστοιχεία είναι το Minecraft της εταιρίας Mojang, θυγατρικής της Microsoft Studios. Ο εικονικός κόσμος του παιχνιδιού αποτελείται αποκλειστικά από ογκοστοιχεία, δίνοντας στην εφαρμογή έναν ιδιαίτερο χαρακτήρα.
|
1. fillVolume(x,y,z)
2. {
3. Color c;
4. C=getColor(x,y,z);
5. If (c<>fill_color)
6. {
7. setPixel(x,y,z,color);
8. fillVolume(x-1,y-1,z);
9. fillVolume(x,y+1,z);
10. fillVolume(x+1,y+1,z);
11. fillVolume(x+1,y,z);
12. fillVolume(x+1,y+1,z);
13. fillVolume(x,y+1,z);
14. fillVolume(x-1,y+1,z);
15. fillVolume(x-1,y,z);
16. fillVolume(x-1,y-1,z+1);
17. fillVolume(x,y,z+1);
18. fillVolume(x,y+1,z+1);
19. fillVolume(x+1,y+1,z+1);
20. fillVolume(x+1,y,z+1);
21. fillVolume(x+1,y+1,z+1);
22. fillVolume(x,y+1,z+1);
23. fillVolume(x-1,y+1,z+1);
24. fillVolume(x-1,y,z+1);
25. fillVolume(x-1,y-1,z-1);
26. fillVolume(x,y+1,z-1);
27. fillVolume(x,y,z-1);
28. fillVolume(x+1,y+1,z-1);
29. fillVolume(x+1,y,z-1);
30. fillVolume(x+1,y+1,z-1);
31. fillVolume(x,y+1,z-1);
32. fillVolume(x-1,y+1,z-1);
33. fillVolume(x-1,y,z-1);
34. }
35. }
Λίστα 4.2. Ο κώδικας γεμίσματος κλειστών περιοχών με ογκοστοιχεία
Η δομή που εξυπηρετεί καλύτερα τους αλγορίθμους που χειρίζονται ογκοστοιχεία είναι το οκταδικό δέντρο (octree) [Meagher, 1980]. Ως δομή δεδομένων, το οκταδικό δέντρο είναι ένα δέντρο του οποίου κάθε κόμβος έχει ακριβώς 8 απογόνους. Αποτελεί μία από τις πιο διαδεδομένες αναδρομικές μεθόδους διαίρεσης του τρισδιάστατου χώρου. Η εφαρμογή της μεθόδου έχει ως αποτέλεσμα τη διαίρεση του χώρου σε οκτώ υποπεριοχές η οποία συνεχίζεται μέχρι να κατατμηθεί ο χώρος στο μέγεθος του αντικειμένου ή στο μέγεθος του ογκοστοιχείου. Κάθε απόγονος κόμβος προσδιορίζεται με βάση το φυσικό κέντρο του γονέα του, ενώ το μέγεθός του μειώνεται καθώς τα επίπεδα αυξάνονται (προς τα κάτω όπως φαίνεται στην Εικόνα 4.13). Αν ένας κόμβος περιγράφει πλήρως την περιοχή που καταλαμβάνει και δεν υπάρχει λόγος περαιτέρω διαίρεσης, τότε ο κόμβος αυτό είναι φύλλο του οκταδικού δέντρου.
Η λογική πίσω από την κωδικοποίηση με ογκοστοιχεία είναι ότι χρησιμοποιείται ένα πολύ απλό στερεό, ο κύβος, κατά τρόπο που δεν εξαρτάται από την πολυπλοκότητα του αντικειμένου. Τα αντικείμενα μπορούν να παρουσιάζουν σύνθετη μορφολογία, να έχουν οπές και ανοίγματα και να περιλαμβάνουν επιφάνειες ελεύθερης μορφής.
Η Κατασκευαστική Στερεά Γεωμετρία (Constructive Solid Geometry - CSG) είναι ένας τρόπος περιγραφής στερεών που ξεκίνησε με σκοπό να χειριστεί βιομηχανικά προϊόντα. Ξεκινώντας από μια βασική συλλογή στερεών μοντέλων (primitives) όπως είναι η σφαίρα, ο κύβος, ο κύλινδρος, η πυραμίδα και κάθε ορθογωνικής διατομής στερεό, το μοντέλο αυτό προσπαθεί με λογικές πράξεις στερεών να μοντελοποιήσει πιο σύνθετα αντικείμενα. Για παράδειγμα, η πράξη της συγκόλλησης μεταξύ δύο στερεών είναι ουσιαστικά η ένωση συνόλων, ενώ το άνοιγμα μιας οπής προκύπτει από τη λογική αφαίρεση του στερεού Α από το στερεό Β, όπου το Α είναι ένας σωλήνας. Αυτό που απομένει είναι ένα στερεό σώμα που περιλαμβάνει όλα τα σημεία που ανήκουν στο Β και ταυτόχρονα δεν ανήκουν στο Α. Μετακινώντας το στερεό Α στο χώρο και αλλάζοντας τον προσανατολισμό του μπορούμε να αλλάξουμε θέση στην οπή και αλλάζοντας το μέγεθός της μπορούμε να αυξομειώνουμε τη διατομή της οπής. Το μοντέλο της στερεάς γεωμετρίας αναπαρίσταται σχηματικά ως δέντρο που έχει ως φύλλα τα αρχικά στερεά (primitives) και ως ρίζα το τελικό μοντέλο στερεού. Ένα παράδειγμα κατασκευής μοντέλου CSG παρουσιάζεται στην Εικόνα 4.14.
Εικόνα 4.13. Διαίρεση του χώρου με τη δομή οκταδικό δέντρο (octree)
Εικόνα 4.14. Δέντρο μοντέλου Constructive Solid Geometry
Η ευκολία εφαρμογής απλών μετασχηματισμών πάνω στα στερεά που συνθέτουν το μοντέλο οδηγεί σε εύκολες αλλαγές στην τελική έκδοση του μοντέλου. Μια αύξηση στο μέγεθος της κούπας που φαίνεται στο προηγούμενο παράδειγμα δε θα ήταν το ίδιο εύκολη στο πολυγωνικό μοντέλο. Στα μειονεκτήματα του CSG συγκαταλέγεται η περιορισμένη γκάμα πράξεων μεταξύ στερεών και η δυσκολία δημιουργίας δισδιάστατων εικόνων από τα μοντέλα CSG.
Το Μοντέλο των Συστημάτων Σωματιδίων (Particle Systems) είναι ιδανικό για παράσταση αντικειμένων που δεν μπορούν να περιγραφούν γεωμετρικά, δεν έχουν σαφώς προσδιορισμένα περιγράμματα, είναι ημιδιάφανα ή έχουν νόημα όταν έρχονται σε σμήνη ή νέφη. Χρησιμοποιούνται για να παραστήσουν φυσικά φαινόμενα και να προσθέσουν ειδικά εφέ στις ταινίες και τα βιντεοπαιχνίδια. Με τα μοντέλα που έχουμε εξετάσει μέχρι τώρα, η φωτιά, ο καπνός, ή ένα νεφέλωμα δε θα μπορούσαν να παρασταθούν ικανοποιητικά. Η βασική δομή σε αυτό το μοντέλο είναι το στοιχειώδες αντικείμενο (particle) που συνήθως έχει μικρές διαστάσεις και δημιουργεί πολλά αντίγραφα του εαυτού του. Ο τυπικός αριθμός των αντιγράφων κυμαίνεται από δεκάδες έως χιλιάδες, ενώ δεν είναι πλέον σπάνιες οι περιπτώσεις συστημάτων που διαχειρίζονται εκατομμύρια particles σε μια σκηνή.
Κατά κανόνα τα particles έχουν κάποια φυσική σημασία, θεωρούνται ασύνδετα και ανεξάρτητα μεταξύ τους, έχουν συγκεκριμένο χρώμα ή υφή που προέρχεται από ψηφιακή εικόνα, έχουν ημιδιάφανο περίγραμμα για να μην είναι ευδιάκριτα τα όρια που τελειώνει το ένα αντικείμενο και αρχίζει το επόμενο. Όταν μάλιστα έχουν μικρό κύκλο ζωής, τότε η συνεχόμενη δημιουργία particles (particle generator) είναι αυτό που προσεγγίζει το φυσικό φαινόμενο. Άλλες φορές ένα σύστημα σωματιδίων έχει νόημα μόνο όταν υπάρχει ταυτόχρονα κίνηση προς μια κατεύθυνση, όπως για παράδειγμα ο προωθητής ενός πυραύλου, ή όταν τα στοιχειώδη αντικείμενα υπακούουν στους φυσικούς νόμους όπως για παράδειγμα οι σπίθες που πετάγονται από το ηλεκτρόδιο μιας συσκευής ηλεκτροκόλλησης και ακολουθούν βαλλιστικές τροχιές.
Τα συστήματα σωματιδίων διαθέτουν έναν πομπό ή πηγή (emitter) που έχει ιδιότητες θέσης, προσανατολισμού και ταχύτητας στον 3Δ χώρο. Συνήθως ο πομπός είναι ένα μη-ορατό αντικείμενο και γίνεται αντιληπτό μέσα από την παραγωγή των particles σε χρόνο εκτέλεσης. Μπορεί, μάλιστα, να είναι δυναμικά μεταβαλλόμενο ως προς οποιαδήποτε ιδιότητά του, π.χ. να ακολουθεί μια διαδρομή στο χώρο (path), ή να υπακούει στους νόμους της φυσικής (π.χ. βαρύτητα).
Ένα μοντέλο συστήματος σωματιδίων είναι ολοκληρωμένο όταν έχουν οριστεί οι ιδιότητες του στοιχειώδους αντικειμένου και του πομπού. Αυτό που αυξάνει το ρεαλισμό στην οπτική απόδοση ενός συστήματος σωματιδίων είναι ο τυχαίος παράγοντας που εισέρχεται στις ιδιότητες των στοιχειωδών σωματιδίων. Για παράδειγμα, ο παράγοντας της τύχης στην κατεύθυνση των σωματιδίων στην Εικόνα 4.15 (direction randomness) έχει ρυθμιστεί στις 30 μοίρες, παράγοντας που προστίθεται στον προσανατολισμό του πομπού για να δημιουργήσει το ‘στεφάνι’ της φλόγας.

 Παράδειγμα συστήματος σωματιδίων
Παράδειγμα συστήματος σωματιδίων
|
Ιδιότητες των particles
|
Εικόνα 4.15. Παράδειγμα συστήματος σωματιδίων για την παράσταση προωθητήρα πυραύλου
Στη δυναμική συμπεριφορά των στοιχειωδών σωματιδίων συγκαταλέγεται η μεταβολή των ιδιοτήτων τους με το χρόνο ή και η αλληλεπίδραση των σωματιδίων μεταξύ τους. Παρατηρούμε ότι στο παράδειγμα του πυραυλικού προωθητήρα, τα στοιχειώδη σωματίδια ‘γεννιούνται’ με κίτρινο χρώμα, ενώ όσο ωριμάζουν στη σύντομη ζωή των 45 με 50 frames, το χρώμα τους μετατρέπεται σταδιακά σε κόκκινο για να προσεγγίσουν την πραγματικότητα. Τα σωματίδια αποτελούνται από απλά γεωμετρικά σχήματα ή πιο συχνά 2Δ επιφάνειες (τετράγωνα ή δίσκοι) που είναι προσανατολισμένες προς το χρήστη. Τέλος, υπάρχουν τα συστήματα σωματιδίων τύπου N-particle τα οποία αποτελούν χρήσιμο εργαλείο σε συστήματα προσομοίωσης, όπως αυτά της υπολογιστικής υδροδυναμικής ή της αστροφυσικής (π.χ. προσομοίωση της δυναμικής εξέλιξης των αστρικών συμπλεγμάτων).
Οι δομές παράστασης που θα μελετηθούν στο κεφάλαιο αυτό είναι δομές δεδομένων που χρησιμοποιούνται για το χειρισμό των πολυγωνικών μοντέλων. Διαφέρουν μεταξύ τους στους τύπους των μοντέλων που αναπαριστούν και στις μεταπληροφορίες του μοντέλου, δηλαδή στις υπόλοιπες πληροφορίες που αφορούν το ίδιο το μοντέλο και παράγονται έμμεσα από αυτό. Στα ενδότερα του πολυγωνικού μοντέλου, η δομή στοιχειοθετείται από μια λίστα τοπολογικών αντικειμένων όπως έδρες, ακμές και κορυφές που οριοθετούνται με βάση γεωμετρικά αντικείμενα (επιφάνειες, καμπύλες και σημεία). Σε αυτό το σημείο μπορεί να σημειωθεί ότι τοπολογία είναι η μελέτη των σχημάτων που δεν προϋποθέτει καμία πληροφορία -ούτε προβληματισμό- σχετικά με τις συντεταγμένες τους.
Το πολυγωνικό μοντέλο είναι ιεραρχικό καθώς ένα σύνολο κορυφών ενώνονται μεταξύ τους, για να σχηματίσουν πολύγωνα, τα οποία με τη σειρά τους σχηματίζουν τις επιφάνειες. Έτσι, ένα σύνολο από επιφάνειες αποτελούν το 3Δ αντικείμενο. Παρακάτω θα εξεταστούν διάφορες δομές δεδομένων που χρησιμοποιούνται στην υλοποίηση των διαφόρων τρόπων παράστασης του πολυγωνικού μοντέλου.
Υπάρχουν διάφορες προσεγγίσεις για τις δομές δεδομένων που χρησιμοποιούνται στο πρόβλημα της παράστασης και κάθε προσέγγιση χρησιμοποιεί διαφορετικές δομές δεδομένων ανάλογα με τους στόχους και τον τρόπο λειτουργίας της [Smith, 2000]. Για παράδειγμα, μια επιφάνεια μπορεί να θεωρηθεί από την άποψη της εσωτερικής της δομής ως ένα πλέγμα πολυγώνων που αποθηκεύει μια λίστα κορυφών και μια ομάδα πολυγώνων που τις χρησιμοποιεί για να προσδιορίσει τις έδρες του αντικειμένου. Ένα τέτοιο πλέγμα έδρας-κορυφής είναι η δεικτοδοτημένη λίστα εδρών (Face-Vertex Mesh).
Η δομή που φαίνεται στην Εικόνα 4.16αποκαλύπτει το μεγάλο πλεονέκτημα αυτής της προσέγγισης: οι αλλαγές στο σχήμα της επιφάνειας, αλλά όχι και στη δομή της, συνεπάγονται αλλαγή μόνο στον πίνακα των κορυφών. Ο πίνακας των εδρών παραμένει σταθερός και αναλλοίωτος (Πίνακας 4.2). Στα μειονεκτήματα της Face-Vertex περιγραφής συγκαταλέγεται η δυσκολία χειρισμού κατάτμησης και ενοποίησης επιφανειών.
Εικόνα 4.16. Μια επιφάνεια του πολυγωνικού μοντέλου που έχει αποδοθεί ως πλέγμα πολυγώνων
Πίνακας 4.2. Λίστες εδρών και κορυφών για τη δομή face-vertex
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Σημείωση: Η προσέγγιση αυτή υιοθετείται από γνωστά μορφότυπα τρισδιάστατων αντικειμένων, όπως είναι το OBJ (Wavefront Technologies), το οποίο είναι ένα ανοιχτό πρότυπο και υποστηρίζεται από τα περισσότερα συστήματα γραφικών.
|
Η πτερωτή ακμή (Winged-Edge Mesh) [Baumgart, 1972] είναι μια δομή που δίνει βαρύτητα στις ακμές. Σύμφωνα με αυτή κάθε ακμή δείχνει σε δύο κορυφές και ενώνει τις δύο έδρες αμφότερων πλευρών και τις 4 ακμές που βρίσκονται σε επαφή με αυτές. Αυτή η τεχνική καταφέρνει να επεξεργαστεί με μεγαλύτερη ευελιξία τις αλλαγές της γεωμετρίας μιας επιφάνειας, αλλά έχει υψηλότερες απαιτήσεις σε μνήμη και χώρο αποθήκευσης σε σχέση με τη δεικτοδοτημένη λίστα εδρών. Η περιπάτηση των άκρων ενός αντικειμένου που αναπαρίσταται με αυτήν την τεχνική είναι πιο εύκολη καθώς για κάθε ακμή διατηρείται μια λίστα με τις γειτονικές της. Αυτό βοηθάει τον αλγόριθμο περιπάτησης να γνωρίζει σε ποια ακμή θα μεταβεί ο έλεγχος μετά από κάθε βήμα. Ο Πίνακας 4.3 δίνει ένα παράδειγμα των δομών Winged-Vertex.
Πίνακας 4.3. Λίστες εδρών, ακμών και κορυφών για τη δομή Winged-edge
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Πίνακας Ακμών | ||||
|---|---|---|---|---|
| # | Κορυφές | Έδρες | Γειτονικές Ακμές | |
| E0 | V0 | V1 | F0 | Ε1 Ε9 |
| E1 | V0 | V2 | F0 F1 | Ε2 Ε3 Ε9 E0 |
| E2 | V0 | V3 | F1 | Ε1 Ε3 |
| E3 | V2 | V3 | F1 F2 | E1 Ε2 Ε4 Ε7 |
| E4 | V3 | V4 | F2 | Ε3 Ε7 |
| E5 | V4 | V5 | F3 | Ε6 Ε7 |
| E6 | V2 | V5 | F3 F4 | Ε5 Ε7 Ε9 E8 |
| E7 | V2 | V4 | F2 F3 | Ε3 Ε4 Ε5 E6 |
| E8 | V1 | V3 | F4 | Ε6 Ε9 |
| E9 | V1 | V2 | F0 F4 | Ε0 Ε1 E6 Ε8 |
Για κάθε ακμή μας ενδιαφέρουν οι κορυφές της, η αριστερή και η δεξιά γειτονικές έδρες, όπως και οι γειτονικές της ακμές. Κάθε ακμή έχει κατεύθυνση ανάγνωσης και έτσι διαβάζεται δύο φορές, μία για κάθε επιφάνεια που ενώνει. Ας πάρουμε για παράδειγμα την ακμή Ε1 από την Εικόνα 4.17. Συνδέει τις κορυφές V0 και V1, γειτνιάζει από τα αριστερά με την F1 και από τα δεξιά με την F2. Επίσης, οι γειτονικές της έδρες περιλαμβάνουν τις ακμές Ε2-Ε4 από την F1 και τις Ε3-Ε5 από την F0. Οι ακμές διαβάζονται με φορά σύμφωνη με τους δείκτες του ρολογιού. Σε μια πιο αυστηρή μορφή από εκείνη που αναπαριστά ο , η Λίστα 4.3 δίνει ένα παράδειγμα υλοποίησης της κλάσης Winged-Edge.
Αν θέλουμε να συγκρίνουμε τις απατήσεις μνήμης της πτερωτής ακμής σε σχέση με τη δεικτοδοτημένη λίστα εδρών, τότε λαμβάνουμε υπόψη ότι κάθε έδρα δεικτοδοτεί στις ακμές της και κάθε ακμή δεικτοδοτεί σε δύο κορυφές και στα δύο ζεύγη γειτονικών ακμών της, χαρακτηριστικό από το οποίο παίρνει και το όνομά της η πτερωτή ακμή. Σύμφωνα με τα παραπάνω, το Winged-Edge χρειάζεται 192 δείκτες για να χειριστεί έναν κύβο και ξεπερνά σε κατανάλωση πόρων μνήμης οποιοδήποτε άλλο μοντέλο έχουμε συζητήσει.
1. class winged-edge
2. {
3. public string name;
4. public vertice vstart;
5. public vertice vend;
6. public face fleft;
7. public face fright;
8. public traverse trav_left[2];
9. public traverse trav_right[2];
10. //constructor
11. public winged-edge(str name, vertice from, vertice to,
12. face left, face right, traverse ltrav[], traverse rtrav[],)
13. {
14. name(this) = name;
15. vstart = from;
16. vend = to;
17. fleft = left;
18. fright = right;
19. trav_left[0] = ltrav[0]; //predessessor
20. trav_left[1] = ltrav[1]; //successor
21. trav_right[0] = rtrav[0]; //predessessor
22. trav_right[1] = rtrav[1]; //successor
23. }
24. }
Λίστα 4.3. Ψευδοκώδικας της κλάσης Winged-Edge
Εικόνα 4.17. Οπτική αναπαράσταση της δομής Πτερωτή Ακμή (Winged-Edge)
Τι γίνεται, όμως, στην περίπτωση που μια επιφάνεια έχει οπές στο εσωτερικό της; Προφανώς η προσέγγιση της πτερωτής ακμής δεν μπορεί να λειτουργήσει ως έχει. Είτε η οπή βρίσκεται ως νησίδα στο εσωτερικό της επιφάνειας είτε παρουσιάζεται ως ‘βαθούλωμα’ της επιφάνειας (Εικόνα 4.18), προτείνονται δύο τρόποι αντιμετώπισης [Shene, 2014]:
Αντιστροφή φοράς ανάγνωσης ακμών (Εικόνα 4.19): Σύμφωνα με αυτή τη λύση μπορούμε να περιδιαβαίνουμε μια επιφάνεια αντιστρέφοντας τη φορά ανάγνωσης των ακμών που ανήκουν στα όρια των οπών.
Προσθήκη βοηθητικής ακμής (Εικόνα 4.20): Η εναλλακτική αντιμετώπιση είναι να υιοθετήσουμε τη λύση των βοηθητικών ακμών σύμφωνα με την οποία στις οπές προστίθενται ακμές που τις ενώνουν με την περιφέρεια έτσι ώστε η ανάγνωση των ακμών να ξεκινήσει δεξιόστροφα (σύμφωνα με τους δείκτες του ρολογιού), αλλά όταν συναντήσει οπή να αλλάξει πορεία (αριστερόστροφη ανάγνωση).
Εικόνα 4.18. Ένα σχήμα που έχει οπή (αριστερά) ή/και βαθούλωμα (δεξιά) παρουσιάζει δυσκολία στην παράστασή του με πτερωτές ακμές (Winged-Edges)
Εικόνα 4.19. Περιδιάβαση ακμών με φορά αντίστροφη των δεικτών του ρολογιού ως λύση στο πρόβλημα των οπών
Εικόνα 4.20. Περιδιάβαση ακμών που ξεκινάει δεξιόστροφα για την επιφάνεια, αλλά αλλάζει πορεία χάρη στην προσθήκη βοηθητικών ακμών που συνδέουν τις οπές με το περίγραμμα της επιφάνειας
Εκτός των άλλων λύσεων υπάρχει, βέβαια, και η συνδυαστική χρήση των δομών που περιγράφονται από τα Face-Vertex και Winged-Edge προκειμένου να προκύψει ένα νέο μοντέλο αναπαράστασης επιφανειών το οποίο συνδυάζει τα πλεονεκτήματα και των δύο προσεγγίσεων (Render Dynamic Mesh). Ένα τέτοιο συνδυαστικό μοντέλο αποθηκεύει τις κορυφές κάθε όψης, τις έδρες κάθε κορυφής και τις έδρες και τις κορυφές κάθε ακμής.
Άλλα μοντέλα ροής αποθηκεύουν την καθεμία επιφάνεια ανεξάρτητα από τις άλλες έτσι ώστε να επιτρέπουν τη σχεδίαση (rendering) των επιφανειών πριν ακόμη ολοκληρωθεί η φόρτωση του αντικειμένου. Σημαντική μπορεί να αποδειχτεί η δυνατότητα αυτή σε περιπτώσεις πολύ μεγάλων αντικειμένων. Άλλες λύσεις προοδευτικής φόρτωσης προσφέρουν από την αρχή μια προσεγγιστική εικόνα του συνολικού αντικειμένου και στην πορεία της φόρτωσης αυξάνουν τη λεπτομέρεια της αναπαράστασης. Η λύση αυτή μπορεί να φανεί ιδιαίτερα χρήσιμη στην περίπτωση που μεγάλα μοντέλα μεταφέρονται μέσω δικτύων περιορισμένου εύρους ζώνης διότι παρέχει σταδιακή εμφάνιση του μοντέλου ενόσω η φόρτωση βρίσκεται σε εξέλιξη.
Σε ειδικές χρήσεις συναντούμε δομές δεδομένων που εξυπηρετούν συγκεκριμένα είδη αντικειμένων. Για παράδειγμα ένας χάρτης ύψους (Heightmap) είναι μια δομή δεδομένων που υλοποιείται ως δισδιάστατος πίνακας και περιέχει ως στοιχεία το ύψος των σημείων του εδάφους. Η μετατροπή του χάρτη ύψους σε πολυγωνικό πλέγμα γίνεται με τη θεώρηση ενός πλέγματος m x n σημείων που αντιστοιχούν στις κορυφές του μοντέλου (Εικόνα 4.21). Οι χάρτες ύψους συνήθως αποδίδονται στην κλίμακα του γκρι και κάθε σημείο τους έχει χρώμα στο διάστημα [0, 255], όπου η μηδενική τιμή (μαύρο χρώμα) αντιστοιχεί στο ελάχιστο ύψος, ενώ η τιμή 255 (λευκό χρώμα) αντιστοιχεί στο μέγιστο ύψος. Οι χάρτες ύψους χρησιμοποιούνται συχνά στη μοντελοποίηση του εδάφους και σε εφαρμογές οπτικοποίησης επιστημονικών δεδομένων.
Εικόνα 4.21. Η δομή δεδομένων ενός χάρτη ύψους (heightmap): α) Μια εικόνα bitmap με τιμές εικονοστοιχείων ανάλογες της πληροφορίας ύψους (πάνω-αριστερά), β) πλέγμα που δείχνει τη μορφολογία του εδάφους (πάνω-δεξιά), γ) η επιφάνεια ως αποτέλεσα της τριγωνοποίησης του πλέγματος σημείων (κάτω-αριστερά) και δ) η επιφάνεια επενδυμένη με υφή (κάτω-δεξιά)
Το πλέγμα ή νέφος σημείων (Point cloud) είναι ένας πολύ απλός τρόπος να παραστήσουμε ένα 3Δ αντικείμενο ή μια σύνθετη σκηνή. Νέφη σημείων δημιουργούνται από τρισδιάστατους σαρωτές που αποτυπώνουν τις μετρήσεις του σε μια μεγάλη λίστα από σημεία, για καθένα από τα οποία αποθηκεύονται οι συντεταγμένες x, y, z και το χρώμα. Παρόλο που τα νέφη σημείων μπορούν να παρασταθούν σε οθόνες απ’ ευθείας (Εικόνα 4.22), συνήθως αποτελούν το πρώτο βήμα μιας διασωληνωμένης διαδικασίας (pipeline) που οδηγεί στη δημιουργία μοντέλων.
Εικόνα 4.22. Μοντέλο αυτοκινήτου (το ίδιο με την Εικόνα 4.11) που προβάλλεται ως νέφος σημείων σε έναν online xyz viewer
Αργότερα, τα σημεία αυτά ενώνονται μεταξύ τους σε έδρες για να σχηματίσουν επιφάνειες με τη βοήθεια του κατάλληλου λογισμικού. Μια σημαντική εφαρμογή του νέφους σημείων υπάρχει στο χώρο της βιομηχανικής τομογραφίας όπου ένα βιομηχανικό προϊόν σαρώνεται για να δημιουργηθεί μια τρισδιάστατη αναπαράστασή του και η οποία στη συνέχεια συγκρίνεται με το μοντέλο CAD για να διαπιστωθούν τυχόν διαφορές.
Παρά τα πλεονεκτήματα του πολυγωνικού μοντέλου, όταν το επίπεδο λεπτομέρειας αυξάνεται, αυξάνονται και οι απαιτήσεις σε μνήμη και επεξεργαστική ισχύ. Η λύση σε αυτό το πρόβλημα είναι η απλοποίηση των μοντέλων, δηλαδή η μετατροπή τους σε μοντέλα με μικρότερο συνολικό αριθμό εδρών. Η ποιότητα της μετατροπής κρίνεται από τη διατήρηση της εμφάνισης και της δομής του αρχικού μοντέλου.
Υπάρχουν διάφορες μέθοδοι απλοποίησης για τις πολυγωνικές επιφάνειες. Δύο μεγάλες οικογένειες είναι: α. αυτή που παράγει διακριτά επίπεδα λεπτομέρειας για το αρχικό αντικείμενο και β. αυτή που παράγει συνεχή επίπεδα λεπτομέρειας. Στην πρώτη περίπτωση, αφού οριστεί ο επιθυμητός αριθμός επιφανειών, παράγεται ένα νέο μοντέλο του αντικειμένου. Υπάρχει η δυνατότητα επαναληπτικής χρήσης του αλγορίθμου για περαιτέρω μείωση του συνολικού αριθμού των στοιχειωδών επιφανειών. Στη δεύτερη περίπτωση, η απλοποίηση έχει μεγαλύτερη προσαρμοστικότητα, καθώς είναι συνεχής και παράγει όλα τα ενδιάμεσα επίπεδα λεπτομέρειας. Μπορεί, μάλιστα, να λειτουργήσει και αντίστροφα για να βοηθήσει στην τελική επιλογή του επιθυμητού επιπέδου λεπτομέρειας, ενώ επιτυγχάνει καλύτερη αντιμετώπιση των λεπτομερειών του μοντέλου. Υπάρχει και η δυνατότητα τμηματικής εφαρμογής των δύο μεθόδων απλοποίησης, προκειμένου να χειριστούν λεπτομέρειες χωρίς να επηρεάζεται το σύνολο του αναπαριστώμενου αντικειμένου.
Στη λύση του LOD, όπως είδαμε προηγούμενα, μπορεί να υπάρχουν απότομες αλλαγές του επιπέδου λεπτομέρειας, αλλαγές ανιχνεύσιμες και ενοχλητικές για το ανθρώπινο μάτι. Αντίθετα οι αλγόριθμοι συνεχούς απλοποίησης είναι απαλλαγμένοι από αυτά τα προβλήματα. Οι περισσότεροι αλγόριθμοι αναζητούν μια νέα θέση για τις κορυφές του μοντέλου έτσι ώστε η διαφορά του αρχικού μοντέλου από το τελικό να συγκρατείται σε λογικά επίπεδα. Παρακάτω θα εξετάσουμε μια σειρά αλγορίθμων που χρησιμοποιούνται στα σύγχρονα συστήματα γραφικών για να λύσουν το πρόβλημα της Απλοποίησης.
Η ομαδοποίηση κορυφών (Vertex Clustering) [Rossignac & Borrel, 1993] είναι μια απλή μέθοδος απλοποίησης πολυγωνικών αντικειμένων που βασίζεται στην ιδέα της μείωσης του αριθμού των κορυφών, η οποία με τη σειρά της έχει ως αποτέλεσμα τη μείωση του συνολικού αριθμού των εδρών. Μπορεί να δεχθεί ως είσοδο οποιαδήποτε πολυγωνικό μοντέλο και εφαρμόζεται σε τρία βασικά στάδια:
Το τελικό σημείο που έχει επιλεγεί ως ‘εκπρόσωπος’ των υπολοίπων σημείων ενός κελιού, δεν τοποθετείται αναγκαστικά στο κέντρο του κελιού ούτε στη θέση κάποιας προϋπάρχουσας κορυφής. Η νέα θέση μπορεί να υπολογιστεί με βάση τη σημαντικότητα του σημείου ή με βάση το μέσο όρο όλων των κορυφών.
Γενικά πρόκειται για μια γρήγορη μέθοδο, αλλά με συχνά μέτρια ποιότητα αποτελεσμάτων καθώς μαζί με τις έδρες καταρρέει συχνά και η τοπολογία του μοντέλου. Στην Εικόνα 4.23 για παράδειγμα, η ομαδοποίηση των κορυφών στις περιοχές Α1 και C2 έδωσε ένα ικανοποιητικό αποτέλεσμα. Αντίθετα, στην περιοχή Α3 βλέπουμε πως η τοπολογία έχει αλλοιωθεί εξαιτίας της ομαδοποίησης που έγινε στην B3, με εμφανείς επιπτώσεις στην τελική μορφή του μοντέλου.
Εικόνα 4.23. Παράδειγμα απλοποίησης πολυγωνικού μοντέλου με ομαδοποίηση κορυφών
Η συγχώνευση ακμών (Edge Collapse) είναι μια παρέμβαση τοπικού χαρακτήρα πάνω σε ένα τριγωνικό πλέγμα που εφαρμόζεται διαδοχικά για την απλοποίηση του μοντέλου [Hoppe, 1996; όπ. αναφ. στο Θεοχάρης κ.α., 2010]. Η βασική αρχή είναι η αφαίρεση μιας ακμής και των δύο εφαπτόμενων τριγώνων έτσι ώστε στο τελικό αποτέλεσμα να έχει συρρικνωθεί η ακμή σε μια κορυφή. Υπολογίζεται ένα σφάλμα απλοποίησης έτσι ώστε να γίνει κατάταξη των ακμών σε αύξουσα σειρά, ανάλογα με το μέγεθος του σφάλματος που εισάγουν. Οι ακμές, η αφαίρεση των οποίων έχει την μικρότερη επίδραση στο μοντέλο, αφαιρούνται πρώτες. Μετά από κάθε συγχώνευση (ή κατάρρευση) ακμής, οι προτεραιότητες υπολογίζονται από την αρχή. Ο αλγόριθμος επαναλαμβάνεται μέχρι να επιτευχθεί ένα μέγιστο επιτρεπόμενο σφάλμα απλοποίησης ή μέχρι ο αριθμός των εδρών να φτάσει το επιθυμητό.
Η νέα κορυφή που προκύπτει από τη συγχώνευση ακμών μπορεί να τοποθετηθεί είτε σε ένα από τα δύο άκρα της εκλιπούσας ακμής, είτε στο μέσον της. Σε άλλες περιπτώσεις η νέα θέση υπολογίζεται με βάση την ελαχιστοποίηση μιας συνάρτησης σφάλματος. Για παράδειγμα, με τη χρήση του τετραγωνικού μέτρου σφάλματος (quadric error metric) είναι δυνατή η ελαχιστοποίηση της τετραγωνικής απόστασης της κορυφής που προκύπτει από τις γύρω όψεις, δηλαδή στη γειτονιά της καταρρέουσας ακμής [Garland & Heckbert, 1997; όπ. αναφ. Θεοχάρης κ.ά., 2010]. Έτσι, αν Δ είναι ένα τρίγωνο που βρίσκεται πάνω στο επίπεδο:
{Εξ. 4.20} |
Τότε η τετραγωνική απόσταση ενός σημείου Α(z, y, z) από το επίπεδο αυτό υπολογίζεται σε:
{Εξ. 4.21} |
Σε κάθε βήμα του αλγορίθμου υπολογίζεται το άθροισμα των τετραγωνικών αποστάσεων κάθε κορυφής από τις γύρω έδρες:
{Εξ. 4.22} |
Όπου n είναι ο αριθμός των εδρών γύρω από την κορυφή Δ και WΔ είναι το εμβαδόν της έδρας Δ. Το εμβαδόν κάθε έδρας προστίθεται στον υπολογισμό του κάθε όρου του αθροίσματος για να προσδώσει βάρος (κλιμάκωση). Άλλες συναρτήσεις σφάλματος συνυπολογίζουν και το εμβαδόν της νέας έδρας που πρόκειται να δημιουργηθεί από τη συγχώνευση ακμών θεωρώντας ένα άνω όριο επιφανείας. Η συγχώνευση ακμών προσφέρει συνεχές επίπεδο λεπτομέρειας και ως διαδικασία είναι εύκολα αναστρέψιμη, δηλαδή μπορεί να δώσει διάσπαση κορυφής (vertex split) για να αυξήσει τον αριθμό των εδρών Εικόνα 4.24.
Εικόνα 4.24. Το αποτέλεσμα της συναίρεσης ζεύγους κορυφών που ανήκουν στην ίδια ακμή (συγχώνευση ακμών-προς τα αριστερά) και η αντίστροφή της διαδικασία που είναι η διάσπαση κορυφής (προς τα δεξιά)
Η απλοποίηση των πολυγωνικών μοντέλων, δηλαδή η μείωση της πολυπλοκότητάς τους και του όγκου των πληροφοριών που φέρουν αυτά, μπορεί να χρησιμοποιηθεί συνδυαστικά με άλλες προσεγγίσεις, όπως είναι το δυναμικό Level of Detail (LOD). Σύμφωνα με αυτό, τα πολυγωνικά μοντέλα υποστηρίζουν πολλαπλές αναλύσεις για χρήση ανά περίπτωση και έτσι προσφέρουν μια ρεαλιστική λύση στο πρόβλημα της σπατάλης πόρων και υπολογιστικής ισχύος για λεπτομερή αντικείμενα τα οποία τελικά θα καταλάβουν επιφάνεια μερικών εικονοστοιχείων.
Ανάλογα με την απόσταση παρατήρησης (μέγεθος του αναπαριστώμενου αντικειμένου στην οθόνη) χρησιμοποιείται η κατάλληλη ‘έκδοση’ του αντικειμένου. Ξεκινώντας από πολύ μικρές αποστάσεις παρατήρησης όπου το μοντέλο εμφανίζεται με τη μέγιστη πληροφορία, σταδιακά χρησιμοποιούνται αντίγραφα μικρότερης πληροφορίας σε κβαντισμένες αποστάσεις από το σημείο παρατήρησης (Εικόνα 4.25).
Εικόνα 4.25. Ένα παράδειγμα πολυγωνικού μοντέλου με δύο στάθμες λεπτομέρειας (πολυπλοκότητας): ελάχιστη πληροφορία (αριστερά) και μέγιστη πληροφορία (δεξιά)
Αν και δεν αποτελεί λειτουργικότητα που προσφέρεται από το μοντέλο αλλά από τις εφαρμογές που τα υποστηρίζουν, η επιλογή του κατάλληλου επιπέδου λεπτομέρειας σε συνάρτηση με την απόσταση από τον παρατηρητή είναι μια ρεαλιστική λύση που συγκρατεί το υπολογιστικό κόστος και προσφέρει στο μάτι του θεατή μια εντύπωση συνέχειας στην αναπαράσταση του αντικειμένου σε δυναμικά μεταβαλλόμενα γραφικά περιβάλλοντα. Σε όσα γραφικά περιβάλλοντα υποστηρίζεται η πλοήγηση ή περιήγηση (navigation), συνήθως υπάρχει μια εικονική κάμερα που αναπαριστά την οπτική γωνία του παρατηρητή. Το σύστημα γραφικών αποφασίζει σε χρόνο εκτέλεσης ποια εκδοχή του μοντέλου θα δείξει ανάλογα με την απόσταση της εικονικής κάμερας από το μοντέλο. Ο επιλογέας βασίζεται σε εξισώσεις επιλογής της μορφής:
{Εξ. 4.23} |
όπου:
LOD(l): Νικητήριο επίπεδο LOD
LOD0, LOD1, LOD2, …, LODn-1: n επίπεδα LOD και αντίστοιχες στάθμες απόστασης
R0, R1, R2, …, Rn-1: στάθμες απόστασης που διαιρούν το χώρο από το 0 στο άπειρο
l: Η απόσταση του παρατηρητή (avatar) από το αντικείμενο
Τα επίπεδα λεπτομέρειας μπορεί να είναι διακριτά (Discrete LOD-DLOD) ή συνεχή (Continuous LOD-CLOD). Επίσης, υπάρχουν επίπεδα λεπτομέρειας που εξαρτώνται από τη γωνία θέασης (View Dependent LoD). Σκεφτείτε την τυπική περίπτωση θέασης ενός 3Δ αντικειμένου σε 2Δ οθόνη με ένα μεγάλο μέρος του αντικειμένου να μην είναι ορατό στο χρήστη. Ούτε οι πίσω επιφάνειες αλλά ούτε και αυτές που κρύβονται από άλλες είναι ορατές ανά πάσα στιγμή. Ο προσανατολισμός μιας επιφάνειας και η θέση της είναι αυτά που καθορίζουν το επίπεδο λεπτομέρειας και από αυτό προκύπτει σημαντικό κέρδος στο πλήθος των εδρών και στην ταχύτητα απόδοσης της σκηνής (frames per second - fps).
Ακόμη και μία μικρή διακύμανση στο framerate, ιδίως όταν αυτό κυμαίνεται κάτω από το επιτρεπτό όριο των 25-30 fps μπορεί να έχει καταστροφικά αποτελέσματα για την ποιότητα της εμπειρίας που αποκομίζει ο χρήστης από την περιήγησή του σε έναν εικονικό κόσμο. Για να αποφευχθεί αυτό, υπάρχουν τεχνικές που φροντίζουν με δεδομένη μια συχνότητα ανανέωσης της σκηνής να επιτύχουν το καλύτερο δυνατό αποτέλεσμα (Fixed Frame Rate Scheduling). Όταν η σκηνή περιλαμβάνει μικρό σχετικά αριθμό πολυγώνων έτσι ώστε να επιτυγχάνεται εύκολα ο επιθυμητός ρυθμός ανανέωσης της σκηνής, τότε επιχειρείται απόδοση με υψηλότερη λεπτομέρεια. Αντίθετα, όταν η σκηνή είναι βεβαρυμμένη με μεγάλο αριθμό πολυγώνων, τότε τα μοντέλα απλοποιούνται στον κατάλληλο βαθμό προκειμένου να ελαφρύνει η σκηνή και να επιτευχθεί το επιθυμητό framerate.

|
4.7. Προτεινόμενες Ασκήσεις και Προβλήματα |
|
Άσκηση 1)
Να βρείτε την εξίσωση της επιφανείας του
Άσκηση 2)
Άσκηση 3)
Άσκηση 4)
|
|