ΚΕΦΑΛΑΙΟ 3. ΓΕΩΜΕΤΡΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΚΑΙ ΠΡΟΒΟΛΕΣ

2015

ΚΕΦΑΛΑΙΟ 3: ΓΕΩΜΕΤΡΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΚΑΙ ΠΡΟΒΟΛΕΣ

3.1. Εισαγωγή
3.2. Γραμμικοί Μετασχηματισμοί
3.3. Γεωμετρικοί Μετασχηματισμοί Συντεταγμένων
3.4. Ομογενείς Συντεταγμένες
3.5. 3Δ Ομογενείς Μετασχηματισμοί
3.6. Προβολές
3.7. Προτεινόμενες Ασκήσεις και Προβλήματα
3.8. Αναφορές

Σύνοψη

Το παρόν κεφάλαιο είναι θεμελιώδες για τα συστήματα γραφικών. Αποτελεί τη βάση για την υλοποίηση πολλών πιο πολύπλοκων διαδικασιών όπως ο φωτισμός, η προβολή και η συνθετική κίνηση. Αρχικά παρουσιάζονται οι γραμμικοί μετασχηματισμοί και οι ιδιότητές τους. Στη συνέχεια περιγράφονται οι δισδιάστατοι μετασχηματισμοί συντεταγμένων και γίνεται μια εισαγωγή στις ομογενείς συντεταγμένες. Ακολουθεί η ανάλυση των ευρύτατα χρησιμοποιούμενων στην πράξη τρισδιάστατων ομογενών συντεταγμένων και το κεφάλαιο κλείνει με τους μετασχηματισμούς προοπτικής και ορθογραφικής προβολής.

Προαπαιτούμενη γνώση

Βασικό υπόβαθρο στη Γραμμική Άλγεβρα. Ευχέρεια στη Διανυσματική Ανάλυση. Στοιχειώδεις γνώσεις Γεωμετρίας και Τριγωνομετρίας.

3.1. Εισαγωγή

Η κίνηση και γενικότερα η δυναμική είναι σήμερα ένα εγγενές στοιχείο των συστημάτων γραφικών. Έτσι πρέπει να υπάρχει η δυνατότητα να αλλάζουν κάποιες ιδιότητες πολλών εκ των αντικειμένων μιας σκηνής. Για παράδειγμα ένα αυτοκίνητο εν κινήσει «μεταφέρει» και «περιστρέφει» τη γεωμετρία του στον εικονικό κόσμο. Ακόμα είναι δυνατό να χρησιμοποιούνται αντίγραφα ενός αντικειμένου (π.χ. δένδρο) σε διαφορετικές κλίμακες και σε διαφορετικές θέσεις. Το μαθηματικό εργαλείο για την υλοποίηση όλων των παραπάνω παραδειγμάτων είναι οι μετασχηματισμοί, οι οποίοι συνθέτουν μία από τις πλέον θεμελιώδεις έννοιες των συστημάτων γραφικών.

3.2. Γραμμικοί Μετασχηματισμοί

Έστω ένα 3Δ σύστημα συντεταγμένων Σ₁, στο οποίο ένα σημείο P εκφράζεται μέσω των συντεταγμένων του (x,y,z). Έστω τώρα ένα δεύτερο σύστημα συντεταγμένων Σ₂, στο οποίο το ίδιο σημείο εκφράζεται μέσω των συντεταγμένων (a,b,c), οι οποίες μπορούν να εκφραστούν ως γραμμικός συνδυασμός των συντεταγμένων (x,y,z) του Σ₁.

$a = w_{1} x + w_{2} y + w_{3} z + t_{1}$
$b = w_{4} x + w_{5} y + w_{6} z + t_{2}$
$c = w_{7} x + w_{8} y + w_{9} z + t_{3}$	{Εξ. 3.1}

Οι παραπάνω σχέσεις ορίζουν ένα γραμμικό μετασχηματισμό του Σ₁ στο Σ₂ που μπορεί να γραφεί ως:

[\begin{matrix} a \\ b \\ c \end{matrix}] = [\begin{matrix} w_{1} & w_{2} & w_{3} \\ w_{4} & w_{5} & w_{6} \\ w_{7} & w_{8} & w_{9} \end{matrix}] [\begin{matrix} x \\ y \\ z \end{matrix}] + [\begin{matrix} t_{1} \\ t_{2} \\ t_{3} \end{matrix}]

{Εξ. 3.2}

Υπό την προϋπόθεση ότι ο μετασχηματισμός είναι αντιστρέψιμος, ο γραμμικός μετασχηματισμός του Σ₂ στο Σ₁ προκύπτει ως:

[\begin{matrix} x \\ y \\ z \end{matrix}] = {[\begin{matrix} w_{1} & w_{2} & w_{3} \\ w_{4} & w_{5} & w_{6} \\ w_{7} & w_{8} & w_{9} \end{matrix}]}^{- 1} ([\begin{matrix} a \\ b \\ c \end{matrix}] - [\begin{matrix} t_{1} \\ t_{2} \\ t_{3} \end{matrix}])

{Εξ. 3.3}

Το διάνυσμα t=(t₁, t₂, t₃) αντιστοιχεί στη μεταφορά της αρχής των αξόνων του Σ_1, ώστε αυτή να συμπέσει με αυτή του Σ_2, ενώ ο πίνακας W, συνήθως, σε επανυπολογισμό των διανυσμάτων βάσης. Στις επόμενες παραγράφους και πιο συγκεκριμένα στους ομογενείς μετασχηματισμούς θα δούμε έναν έξυπνο τρόπο να συνδυάσουμε έναν μετασχηματισμό που απαρτίζεται από έναν 3x3 πίνακα W και ένα διάνυσμα t σε έναν και μόνο πίνακα διάστασης 4x4.

3.3. Γεωμετρικοί Μετασχηματισμοί Συντεταγμένων

Στην παράγραφο αυτή θα συζητήσουμε τους βασικότερους απλούς μετασχηματισμούς, αρχικά στις 2 διαστάσεις και στη συνέχεια θα γενικεύουμε και στις 3 διαστάσεις, περιγράφοντας τις διαφορές που παρουσιάζονται. Οι κύριοι μετασχηματισμοί συντεταγμένων είναι η μεταφορά, η αλλαγή κλίμακας και η περιστροφή.

3.3.1. Μεταφορά

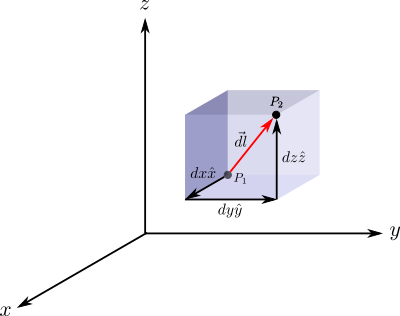
Ο μετασχηματισμός μεταφοράς περιγράφει τη μετακίνηση προς συγκεκριμένη κατεύθυνση κατά συγκεκριμένη απόσταση. Σημαντική πληροφορία για την υλοποίηση του μετασχηματισμού μεταφοράς είναι η ποσότητα της μετακίνησης t_xκαι t_yστον άξονα των x και των y αντίστοιχα. Στις 2Δ, ένα σημείο p₁=(x,y) μπορεί να μεταφερθεί κατά t=(t_x,t_y) και το νέο σημείο p₂ προκύπτει ως εξής:

p_{2} = p_{1} + t = [\begin{matrix} x \\ y \end{matrix}] + [\begin{matrix} t_{x} \\ t_{y} \end{matrix}] = [\begin{matrix} x + t_{x} \\ y + t_{y} \end{matrix}]

{Εξ. 3.4}

Στην Εικόνα 3.1 παρουσιάζεται ένα παράδειγμα μεταφοράς ενός σχήματος στις δύο διαστάσεις.

Εικόνα 3.1. Μεταφορά αντικειμένου με διάνυσμα μετατόπισης (6, -1)

Ο μετασχηματισμός μεταφοράς γενικεύεται εύκολα στις τρεις διαστάσεις, όπως περιγράφει η παρακάτω σχέση:

p_{2} = p_{1} + t = [\begin{matrix} x \\ y \\ z \end{matrix}] + [\begin{matrix} t_{x} \\ t_{y} \\ t_{z} \end{matrix}] = [\begin{matrix} x + t_{x} \\ y + t_{y} \\ z + t_{z} \end{matrix}]

{Εξ. 3.5}

3.3.2. Αλλαγή Κλίμακας

Ο μετασχηματισμός αλλαγής κλίμακας επηρεάζει και μεταβάλλει εξ’ ορισμού το μέγεθος των αντικειμένων. Σημαντική πληροφορία για την υλοποίηση του μετασχηματισμού αλλαγής κλίμακας είναι η ποσότητα της μεγέθυνσης ή σμίκρυνσης s_xκαι s_yστον άξονα των x και των y αντίστοιχα. Στις 2Δ, ένα σημείο p₁=(x,y) μπορεί να κλιμακωθεί με τη χρήση ενός πίνακα κλιμάκωσης S και το νέο σημείο p₂ προκύπτει ως εξής:

p_{2} = S \cdot p_{1} = [\begin{matrix} s_{x} & 0 \\ 0 & s_{y} \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = |\begin{matrix} s_{x} \cdot x \\ s_{y} \cdot y \end{matrix}|

{Εξ. 3.6}

Στην περίπτωση όπου s_x=s_y=s, μιλάμε για ομοιόμορφη αλλαγή κλίμακας, όπου η κλιμάκωση λαμβάνει χώρα με τον ίδιο τρόπο και ως προς τους δύο άξονες. Στην περίπτωση αυτή ο πίνακας S μπορεί να αντικατασταθεί με τη βαθμωτή ποσότητα s.

p_{2} = S \cdot p_{1} = [\begin{matrix} s & 0 \\ 0 & s \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = s [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = s \cdot I \cdot p_{1} = s \cdot p_{1}

{Εξ. 3.7}

Όταν ο συντελεστής κλιμάκωσης έχει τιμή ίση με τη μονάδα, τότε δεν υπάρχει αλλαγή κλίμακας, ενώ μιλάμε για μεγέθυνση ή σμίκρυνση όταν έχει τιμή μεγαλύτερη ή μικρότερη της μονάδας αντίστοιχα. Στην Εικόνα 3.2 παρουσιάζεται ένα παράδειγμα κλιμάκωσης ενός σχήματος στις δύο διαστάσεις.

Εικόνα 3.2. Κλιμάκωση αντικειμένου με διάνυσμα κλιμάκωσης (3, 2)

Η κλιμάκωση ως μετασχηματισμός πολλαπλασιάζει με ένα συντελεστή τις συντεταγμένες ενός αντικειμένου. Έστω τώρα το μαύρο τετράγωνο στο παρακάτω σχήμα, το οποίο θέλουμε να μετασχηματίσουμε ώστε να συμπίπτει με το κόκκινο τετράγωνο. Με μια πρώτη ματιά παρατηρούμε ότι το μέγεθος του αντικειμένου έχει διπλασιαστεί. Άρα ένας μετασχηματισμός ομοιόμορφης κλιμάκωσης κατά 2 S(2,2) ίσως να μας έδινε την απάντηση στο πρόβλημά μας. Δεν είναι όμως έτσι, διότι ο μετασχηματισμός εφαρμόζεται στις συντεταγμένες κάθε σημείου του αντικειμένου. Έτσι αν εφαρμόσουμε την παραπάνω κλιμάκωση αντί να πάρουμε το επιθυμητό αποτέλεσμα της Εικόνας 3.3, θα πάρουμε αντί αυτού το αποτέλεσμα που φαίνεται στην Εικόνα 3.4.

Εικόνα 3.3. Κλιμάκωση αντικειμένου με στόχο το διπλασιασμό του μεγέθους του. Δεν είναι σωστή η επιλογή του μετασχηματισμού S(2,2) διότι πέρα από την κλιμάκωση θα έχουμε και μεταφορά του αντικειμένου επειδή αυτό δεν είναι «κεντραρισμένο» στην αρχή των αξόνων.

Για να μπορέσουμε τώρα να εφαρμόσουμε κλιμάκωση θα πρέπει να χρησιμοποιήσουμε σύνθετους μετασχηματισμούς. Πρέπει, δηλαδή, αρχικά να μεταφέρουμε το αντικείμενο στην αρχή των αξόνων, στη συνέχεια να εκτελέσουμε την επιθυμητή κλιμάκωση και τέλος να το επαναφέρουμε στην επιθυμητή θέση. Οι σύνθετοι μετασχηματισμοί θα αναλυθούν σε επόμενη παράγραφο. Ο μετασχηματισμός κλιμάκωσης γενικεύεται εύκολα στις τρεις διαστάσεις, όπως περιγράφει η παρακάτω σχέση:

p_{2} = S \cdot p_{1} = [\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & s_{z} \end{matrix}] [\begin{matrix} x \\ y \\ z \end{matrix}] = [\begin{matrix} s_{x} \cdot x \\ s_{y} \cdot y \\ s_{z} \cdot z \end{matrix}]

{Εξ. 3.8}

Εικόνα 3.4. Η κλιμάκωση επιφέρει ταυτόχρονα και μεταφορά σε περίπτωση που ένα αντικείμενο δεν είναι τοποθετημένο στην αρχή των αξόνων

3.3.3. Περιστροφή στις 2Δ

Η περιστροφή στις δύο διαστάσεις περιστρέφει ένα αντικείμενο γύρω από την αρχή των αξόνων. Σημαντική πληροφορία για την υλοποίηση του μετασχηματισμού περιστροφής στις δύο διαστάσεις είναι η γωνία περιστροφής θ. Ακόμα υιοθετούμε τη σύμβαση ότι θετική είναι μία περιστροφή κατά φορά αντίθετη αυτής των δεικτών του ρολογιού. Έστω, λοιπόν, το σημείο p₁=(x,y) το οποίο, όπως απεικονίζει η Εικόνα 3.5 πρέπει να περιστραφεί κατά θ μοίρες και να μετασχηματιστεί στο σημείο p₂=(a,b).

Εικόνα 3.5. Περιστροφή κατά θ στις δύο διαστάσεις

Παρατηρώντας την Εικόνα 3.5 και έχοντας υπόψη ότι κατά την περιστροφή το μήκος του διανύσματος Οp παραμένει σταθερό, μπορούμε να εξάγουμε εύκολα τις παρακάτω σχέσεις:

a = ||p|| \cos (φ + θ) = ||p|| (\cos φ \cos θ - \sin φ \sin θ) = x \cos θ - y \sin θ b = ||p|| \sin (φ + θ) = ||p|| (c o s φ \sin θ + s i n φ \cos θ) = x \sin θ - y \cos θ

{Εξ. 3.9}

Η παραπάνω σχέση μπορεί να εκφραστεί και σε μορφή πίνακα ως εξής:

p_{2} = [\begin{matrix} a \\ b \end{matrix}] = [\begin{matrix} \cos θ & - s i n θ \\ \sin θ & c o s θ \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = R (θ) \cdot p_{1}

{Εξ. 3.10}

όπου R(θ) ο πίνακας περιστροφής:

R (θ) = [\begin{matrix} \cos θ & - \sin θ \\ s i n θ & c o s θ \end{matrix}]

{Εξ. 3.11}

Η παρακάτω εικόνα παρουσιάζει ένα παράδειγμα 2Δ περιστροφής ενός αντικειμένου.

Εικόνα 3.6. Περιστροφή αντικειμένου κατά θ στις δύο διαστάσεις

Όπως και η κλιμάκωση έτσι και η περιστροφή ως μετασχηματισμός επηρεάζει τις συντεταγμένες ενός αντικειμένου. Έστω τώρα το μαύρο τετράγωνο στο παρακάτω σχήμα, το οποίο θέλουμε να μετασχηματίσουμε στο κόκκινο τετράγωνο. Θέλουμε, δηλαδή, να εκτελέσουμε μία περιστροφή 90^ο γύρω από το κέντρο βάρους του. Ένας μετασχηματισμός R(90) θα έδινε τη λύση στο πρόβλημά μας; Η απάντηση είναι όχι, διότι ο μετασχηματισμός εφαρμόζεται στις συντεταγμένες κάθε σημείου του αντικειμένου και η περιστροφή λαμβάνει χώρα γύρω από την αρχή των αξόνων. Έτσι, εφαρμόζοντας την παραπάνω περιστροφή αντί να πάρουμε το επιθυμητό αποτέλεσμα (Εικόνα 3.6), θα πάρουμε αντί αυτού το αποτέλεσμα που απεικονίζεται στην Εικόνα 3.7.

Εικόνα 3.7. Περιστροφή αντικειμένου κατά 90^o γύρω από το κέντρο βάρους του

Για να μπορέσουμε τώρα να εφαρμόσουμε την περιστροφή πρέπει να χρησιμοποιήσουμε σύνθετους μετασχηματισμούς. Πρέπει, δηλαδή, αρχικά να μεταφέρουμε το αντικείμενο στην αρχή των αξόνων στη συνέχεια να εκτελέσουμε την επιθυμητή περιστροφή και τέλος να το επαναφέρουμε στην επιθυμητή θέση.

3.3.4. Περιστροφή στις 3Δ

Η σημαντικότερη θεμελιώδης διαφορά της περιστροφής στις τρεις διαστάσεις σε σχέση με τις δύο είναι ότι στις τρεις διαστάσεις δεν ορίζεται περιστροφή γύρω από σημείο, αλλά μπορεί να οριστεί περιστροφή γύρω από άξονα. Έτσι σημαντική πληροφορία για την υλοποίηση του μετασχηματισμού περιστροφής στις τρεις διαστάσεις είναι η γωνία περιστροφής θ και ο άξονας περιστροφής v.

Για την περίπτωση περιστροφής γύρω από έναν από τους τρεις άξονες βάσης του συστήματος συντεταγμένων τα πράγματα είναι απλά. Θεωρώντας την περίπτωση της περιστροφής γύρω από τον άξονα z, τότε έχουμε πρακτικά μια περιστροφή δύο διαστάσεων, κατά την οποία αλλάζουν οι συντεταγμένες x και y, ενώ παραμένει σταθερή η z. Αυτό μπορεί να μοντελοποιηθεί επεκτείνοντας τον 2x2 πίνακα περιστροφής σε πίνακα 3x3 με τη χρήση του μοναδιαίου πίνακα για την τρίτη διάσταση, όπως περιγράφει η παρακάτω σχέση:

R_{z} (θ) = [\begin{matrix} c o s θ & - s i n θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}]

{Εξ. 3.12}

Κατά αναλογία μπορούν να οριστούν και οι πίνακες που εκτελούν περιστροφή κατά γωνία θ γύρω από τον άξονα των x και y αντίστοιχα.

R_{x} (θ) = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ & - \sin θ \\ 0 & s i n θ & c o s θ \end{matrix}]

R_{y} (θ) = [\begin{matrix} c o s θ & 0 & - s i n θ \\ 0 & 1 & 0 \\ s i n θ & 0 & c o s θ \end{matrix}]

{Εξ. 3.13}

3.3.5. Σύνθετοι 2Δ Μετασχηματισμοί

Πρέπει αρχικά να υπενθυμίσουμε ότι εν γένει είναι σημαντική η σειρά με την οποία εφαρμόζονται οι μετασχηματισμοί. Στις παρακάτω εικόνες απεικονίζονται οι διαφορές στην εφαρμογή με διαφορετική σειρά ενός μετασχηματισμού μεταφοράς t(-3,0) και ενός μετασχηματισμού περιστροφής R(90).

Εικόνα 3.8. Εφαρμογή μετασχηματισμού μεταφοράς t(-3,0) και έπειτα μετασχηματισμού περιστροφής R(90)

Όταν ένας μετασχηματισμός εφαρμοστεί σε ένα σημείο μίας σκηνής τότε έχουμε ως αποτέλεσμα ένα νέο σημείο στη σκηνή. Στο αποτέλεσμα μπορούν να εφαρμοστούν στη συνέχεια επιπλέον μετασχηματισμοί. Για παράδειγμα έστω ένα αντικείμενο με 100 σημεία, το οποίο θέλουμε να κλιμακώσουμε με τον πίνακα S, και να περιστρέψουμε με τον πίνακα R. Δηλαδή, κάθε σημείο του αντικειμένου θέλουμε να μετασχηματιστεί ως εξής:

p' = R (S \cdot p)

{Εξ. 3.14}

Η πράξη αυτή ισοδυναμεί με δύο πολλαπλασιασμούς πινάκων για κάθε σημείο, άρα για τα 100 σημεία έχουμε 200 πολλαπλασιασμούς πινάκων. Ωστόσο, αντί να πολλαπλασιάσουμε τον πίνακα S με το σημείο p και στη συνέχεια το αποτέλεσμα με το R, μπορούμε να υπολογίσουμε ένα σύνθετο μετασχηματισμό ο οποίος να συμπεριλαμβάνει το R και το S σε έναν πίνακα και να πολλαπλασιάσουμε το αποτέλεσμα με όλα τα σημεία του αντικειμένου. Στην περίπτωση αυτή έχουμε 100 πολλαπλασιασμούς πινάκων συν 1 για τον υπολογισμό του σύνθετου μετασχηματισμού. Άρα έχουμε:

p' = R (S \cdot p) = (R \cdot s) p = M \cdot p

{Εξ. 3.15}

Εικόνα 3.9. Εφαρμογή μετασχηματισμού περιστροφής R(90) και έπειτα μετασχηματισμού μεταφοράς t(-3,0)

Εδώ πρέπει να προσέξουμε ότι ο πολλαπλασιασμός πινάκων δεν έχει την αντιμεταθετική ιδιότητα, οπότε έχει σημασία η σειρά με την οποία πολλαπλασιάζονται οι πίνακες. Επομένως, όταν θέλουμε να εφαρμόσουμε διαδοχικά ένα σύνολο μετασχηματισμών Μ₁, Μ₂,…, Μ_n, πρέπει να υπολογίσουμε το σύνθετο πίνακα πολλαπλασιάζοντας με αντίστροφη φορά:

M = M_{n} \cdot . . . \cdot M_{2} \cdot M_{1}

{Εξ. 3.16}

Τι γίνεται, όμως, όταν θέλουμε στο σύνθετο μετασχηματισμό μας να εφαρμόσουμε και μεταφορά; Στην περίπτωση αυτή, δυστυχώς, η μεταφορά δεν μπορεί να εκφραστεί ως γραμμικός συνδυασμός των συντεταγμένων του σημείου, δηλαδή με την παρακάτω μορφή:

x'_{p} = a x_{p} + b y_{p} y'_{p} = c x_{p} + d y_{p}

{Εξ. 3.17}

Η μεταφορά ας θυμηθούμε ότι απλώς προσθέτει μία ποσότητα σε κάθε συντεταγμένη:

x'_{p} = x_{p} + t_{x} y'_{p} = y_{p} + t_{y}

{Εξ. 3.18}

Συμπερασματικά δεν μπορεί να συμπεριληφθεί σε έναν σύνθετο μετασχηματισμό όπως περιγράφηκε παραπάνω. Τη λύση στο πρόβλημα αυτό δίνουν οι ομογενείς συντεταγμένες, οι οποίες περιγράφονται αναλυτικά στην επόμενη παράγραφο.

3.4. Ομογενείς Συντεταγμένες

Έστω τώρα ότι θέλουμε να εφαρμόσουμε μία αλλαγή συστήματος συντεταγμένων. Αυτό, συνήθως, απαιτεί μία περιστροφή και μία μεταφορά, ώστε να συμπέσουν οι άξονες. Άρα καταλήγουμε σε ένα μετασχηματισμό της παρακάτω μορφής:

p' = R \cdot p + t

{Εξ. 3.19}

όπου R είναι ο αντιστρέψιμος πίνακας περιστροφής και t το διάνυσμα μεταφοράς. Τι γίνεται, όμως, όταν θέλουμε να επαναλάβουμε άλλον έναν όμοιο μετασχηματισμό με διαφορετικό πίνακα περιστροφής και διάνυσμα μεταφοράς; Αυτή η πολύ κοινή διεργασία στους γράφους σκηνής και στη σκελετική κίνηση, όπως θα περιγράψουμε σε επόμενα κεφάλαια, γίνεται ιδιαίτερα πολύπλοκη, όπως περιγράφεται στην παρακάτω σχέση:

p' = R_{2} (R_{1} p + t_{1}) + t_{2} = (R_{1} R_{2}) p + R_{2} t_{1} + t_{2}

{Εξ. 3.20}

Για n μετασχηματισμούς, η παραπάνω σχέση υποδεικνύει ότι πρέπει να αποθηκεύουμε τους συνδυασμένους πίνακες περιστροφής R_nR_n-1αλλά και τους όρους μεταφοράς R_nt_n-1και t_n.

Οι ομογενείς συντεταγμένες μας παρέχουν τη δυνατότητα με ένα έξυπνο τρόπο να παρακάμψουμε το παραπάνω πρόβλημα και προσθέτοντας μία ακόμα διάσταση να περιγράψουμε καθολικά όλους τους βασικούς μετασχηματισμούς με πίνακες (n+1)x(n+1), όπου n είναι η διάσταση του προβλήματος.

Ένα σημείο δύο διαστάσεων αναπαρίσταται, πλέον, με ένα διάνυσμα τριών στοιχείων προσθέτοντας την ομογενή συντεταγμένη w, την οποία και θέτουμε ίση με 1. Άρα η ομογενής αναπαράσταση του σημείου p θα είναι:

p = {[\begin{matrix} x & y & 1 \end{matrix}]}^{T}

{Εξ. 3.21}

Για ένα δισδιάστατο πρόβλημα μπορούμε να ορίσουμε τον 3x3 ομογενή πίνακα μετασχηματισμού M, ο οποίος συμπεριλαμβάνει και την περιστροφή αλλά και τη μετατόπιση ως εξής:

M = [\begin{matrix} R & t \\ 0 & 1 \end{matrix}] = [\begin{matrix} r_{11} & r_{12} & t_{x} \\ r_{21} & r_{22} & t_{y} \\ 0 & 0 & 1 \end{matrix}]

{Εξ. 3.22}

Ο πίνακας Μ αν πολλαπλασιαστεί με ένα σημείο p, το μετασχηματίζει ακριβώς, όπως η Εξ. 3.20 και έχει ως αποτέλεσμα ένα σημείο με w συντεταγμένη ίση με 1. Όπως θα δούμε στη συνέχεια και στους μετασχηματισμούς προβολής, δεν «αφήνουν» όλοι η μετασχηματισμοί ανεπηρέαστο το w. Στην περίπτωση αυτή μπορούμε να ανακτήσουμε τις καρτεσιανές συντεταγμένες ενός σημείου διαιρώντας όλες τις συντεταγμένες με το w. Δηλαδή:

p = [\begin{matrix} a \\ b \\ w \end{matrix}] \Rightarrow p_{c a r t e s i a n} [\begin{matrix} a / w \\ b / w \\ 1 \end{matrix}] = [\begin{matrix} p_{x} \\ p_{y} \\ 1 \end{matrix}]

{Εξ. 3.23}

3.4.1. Ομογενής 2Δ Κλιμάκωση

Με τις ομογενείς συντεταγμένες μπορούμε να υπολογίσουμε ένα μετασχηματισμό κλιμάκωσης ενός ζεύγους συντεταγμένων βάσει των παρακάτω εξισώσεων:

p_{2} = S \cdot p_{1 =} [\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}] = [\begin{matrix} s_{x} \cdot x \\ s_{y} \cdot y \\ 1 \end{matrix}]

{Εξ. 3.24}

Οπότε η ομογενής κλιμάκωση στις δύο διαστάσεις περιγράφεται από τον παρακάτω πίνακα:

S = [\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{matrix}]

{Εξ. 3.25}

όπου s_x και s_y οι συντελεστές κλιμάκωσης κατά τον άξονα των x και y αντίστοιχα.

3.4.2. Ομογενής 2Δ Περιστροφή

Με τον ίδιο τρόπο μπορεί να επεκταθεί και ο μετασχηματισμός περιστροφής, ώστε να εφαρμόζεται πάνω σε σημεία τα οποία αναπαρίστανται με ομογενείς συντεταγμένες. Για την περιστροφή ενός σημείου μπορεί να χρησιμοποιηθεί η παρακάτω σχέση:

p_{2} = [\begin{matrix} a \\ b \\ 1 \end{matrix}] = [\begin{matrix} \cos θ & - \sin θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}] = R (θ) \cdot p_{1}

{Εξ. 3.26}

Οπότε η ομογενής περιστροφής στις δύο διαστάσεις περιγράφεται από τον παρακάτω πίνακα, όπου θ είναι η γωνία περιστροφής γύρω από την αρχή των αξόνων.

R (θ) = [\begin{matrix} \cos θ & - \sin θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}]

{Εξ. 3.27}

3.4.3. Ομογενής 2Δ Μεταφορά

Ένα από τα προβλήματα τα οποία λύνουν οι ομογενείς συντεταγμένες είναι, όπως αναφέρθηκε και σε προηγούμενη παράγραφο, η δυνατότητα έκφρασης της μεταφοράς ως γραμμικού συνδυασμού των συντεταγμένων εισόδου, δηλαδή με τη χρήση ενός πίνακα 3x3, αντίστοιχου με αυτόν της περιστροφής και της κλιμάκωσης. Πώς, όμως, μπορεί να γίνει κάτι τέτοιο;

Βάσει της συντεταγμένης w των ομογενών συντεταγμένων, η οποία έχει την τιμή 1 για κάθε σημείο (x, y, w) όπου τα x, y αντιστοιχούν σε σημεία του 2Δ κόσμου (αλλιώς θα αντιστοιχούσαν οι συντεταγμένες x/w και y/w σε σημεία του 2Δ κόσμου) μπορούμε να εκφράσουμε τη μεταφορά ως γραμμικό συνδυασμό της εισόδου ως εξής:

p_{2} = [\begin{matrix} a \\ b \\ 1 \end{matrix}] [\begin{matrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}] = T \cdot p_{1}

{Εξ. 3.28}

Οπότε η ομογενής μεταφορά στις δύο διαστάσεις περιγράφεται από τον παρακάτω πίνακα όπου t_x και t_y είναι η μετατόπιση ως προς τον άξονα των x και y αντίστοιχα.

T = [\begin{matrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{matrix}]

{Εξ. 3.29}

3.4.4. Ομογενείς 2Δ Σύνθετοι Μετασχηματισμοί

Πλέον, όλοι οι βασικοί μετασχηματισμοί μπορούν να εκφραστούν ως γραμμικός συνδυασμός των ομογενών συντεταγμένων του σημείου, δηλαδή με την παρακάτω μορφή:

$x'_{p} = a x_{p} + b y_{p} + c w_{p}$
$y'_{p} = d x_{p} + e y_{p} + f w_{p}$
$w'_{p} = g x_{p} + h y_{p} + i w_{p}$	{Εξ. 3.30}

Οπότε, όταν θέλουμε να εφαρμόσουμε διαδοχικά ένα σύνολο μετασχηματισμών Μ₁, Μ₂,…, Μ_n, συμπεριλαμβανομένης της μεταφοράς, πρέπει να υπολογίσουμε το σύνθετο πίνακα πολλαπλασιάζοντας με αντίστροφη φορά:

M = M_{n} \cdot . . . \cdot M_{2} \cdot M_{1}

{Εξ. 3.31}

3.5. 3Δ Ομογενείς Μετασχηματισμοί

Η γενίκευση των 3Δ ομογενών μετασχηματισμών στις τρεις διαστάσεις είναι σχετικά απλή. Στις επόμενες παραγράφους γίνεται η παρουσίασή τους και αναλύονται κάποιες ιδιαιτερότητές τους.

3.5.1. Ομογενής 3Δ Κλιμάκωση

Με τις ομογενείς συντεταγμένες μπορούμε να υπολογίσουμε ένα μετασχηματισμό κλιμάκωσης στις τρεις χωρικές διαστάσεων βάσει των παρακάτω εξισώσεων:

p_{2} = S \cdot p_{1} = [\begin{matrix} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} s_{x} \cdot x \\ s_{y} \cdot y \\ s_{z} \cdot z \\ 1 \end{matrix}]

{Εξ. 3.32}

Οπότε η ομογενής κλιμάκωση στις τρεις διαστάσεις περιγράφεται από τον παρακάτω πίνακα:

S = [\begin{matrix} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.33}

όπου s_x, s_yκαι s_zοι συντελεστές κλιμάκωσης κατά τον άξονα των x, y και z αντίστοιχα. Πολλές φορές είναι χρήσιμο να γνωρίζουμε και τους αντίστροφους μετασχηματισμούς, όταν για παράδειγμα θέλουμε να αναιρέσουμε μία κίνηση σε μία προσομοίωση. Σε γενικές γραμμές ο αντίστροφος Μ^-1 ενός μετασχηματισμού M είναι ο αντίστροφος του πίνακα Μ, οπότε πρέπει να ικανοποιεί την παρακάτω σχέση:

M \cdot M^{- 1} = I

{Εξ. 3.34}

Για την περίπτωση της κλιμάκωσης, ο αντίστροφος μετασχηματισμός μιας κλιμάκωσης (s_x, s_y, s_z) προκύπτει από τον παρακάτω πίνακα:

S^{- 1} = S (\frac{1}{s_{x}}, \frac{1}{s_{y}}, \frac{1}{s_{z}}) = [\begin{matrix} \frac{1}{s_{x}} & 0 & 0 & 0 \\ 0 & \frac{1}{s_{y}} & 0 & 0 \\ 0 & 0 & \frac{1}{s_{z}} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.35}

3.5.2. Ομογενής 3Δ Μεταφορά

Με τις ομογενείς συντεταγμένες μπορούμε να υπολογίσουμε ένα μετασχηματισμό μεταφοράς στις τρεις χωρικές διαστάσεων βάσει των παρακάτω εξισώσεων:

p_{2} = [\begin{matrix} a \\ b \\ c \\ 1 \end{matrix}] [\begin{matrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = T \cdot p_{1}

{Εξ. 3.36}

Οπότε η ομογενής μεταφορά στις δύο διαστάσεις περιγράφεται από τον παρακάτω πίνακα, όπου t_x, t_y και t_z είναι η μετατόπιση ως προς τον άξονα των x και y αντίστοιχα.

T = [\begin{matrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.37}

Για την περίπτωση της μεταφοράς ο αντίστροφος μετασχηματισμός μίας μετατόπισης (t_x, t_y, t_z) προκύπτει από τον παρακάτω πίνακα:

T^{- 1} = T (- t_{x}, - t_{y}, - t_{z}) = [\begin{matrix} 1 & 0 & 0 & - t_{x} \\ 0 & 1 & 0 & - t_{y} \\ 0 & 0 & 1 & - t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.38}

3.5.3. Ομογενής 3Δ Περιστροφή

Με τις ομογενείς συντεταγμένες μπορούμε να υπολογίσουμε ένα μετασχηματισμό περιστροφής κατά γωνία θ, γύρω από έναν από τους άξονες βάσης. Θεωρώντας την περίπτωση της περιστροφής γύρω από τον άξονα z, μπορούμε να υπολογίσουμε την περιστροφή ενός σημείου ως εξής:

p_{2} = [\begin{matrix} a \\ b \\ c \\ 1 \end{matrix}] [\begin{matrix} \cos θ & - \sin θ & 0 & 0 \\ s i n θ & c o s θ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = R_{2} (θ) \cdot p_{1}

{Εξ. 3.39}

Οπότε ο πίνακας ομογενούς περιστροφής γύρω από τον άξονα z έχει ως εξής:

R_{z} (θ) = [\begin{matrix} \cos θ & - \sin θ & 0 & 0 \\ s i n θ & c o s θ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.40}

Κατά αναλογία μπορούν να οριστούν και οι πίνακες που εκτελούν περιστροφή κατά γωνία θ, γύρω από τον άξονα των x και y αντίστοιχα.

R_{x} (θ) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & c o s θ & - s i n θ & 0 \\ 0 & \sin θ & c o s θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

R_{y} (θ) = [\begin{matrix} \cos θ & 0 & - s i n θ & 0 \\ 0 & 1 & 0 & 0 \\ s i n θ & 0 & c o s θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.41}

Για την περίπτωση της περιστροφής ο αντίστροφος μετασχηματισμός προκύπτει, θέτοντας όπου θ το –θ. Οπότε οι αντίστροφοι πίνακες περιστροφής είναι οι εξής:

$R_{x}^{- 1} = R_{x} (- θ) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos θ & \sin θ & 0 \\ 0 & - s i n θ & c o s θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$	$R_{y}^{- 1} = R_{y} (- θ) = [\begin{matrix} \cos θ & 0 & \sin θ & 0 \\ 0 & 1 & 0 & 0 \\ - \sin θ & 0 & c o s θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$
$R_{z}^{- 1} = R_{z} (- θ) = [\begin{matrix} \cos θ & s i n θ & 0 & 0 \\ - s i n θ & c o s θ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$	{Εξ. 3.42}

3.5.4. Περιστροφή Γύρω από Τυχαίο Άξονα

Ο υπολογισμός μίας τυχαίας περιστροφής στις τρεις διαστάσεις είναι ένα αρκετά περίπλοκο πρόβλημα. Εάν κανείς θέλει να συνδυάσει τρεις περιστροφές γύρω από τους άξονες βάσης για να συνθέσει μία τυχαία περιστροφή, πρέπει να είναι ιδιαίτερα προσεκτικός και να λάβει υπόψη ότι οι σύνθετοι μετασχηματισμοί δεν έχουν την αντιμεταθετική ιδιότητα. Δηλαδή, αν εκτελέσει κανείς μία περιστροφή γύρω από τον άξονα των x και μετά μία περιστροφή γύρω από τον άξονα των z, δε θα καταλήξει στο ίδιο αποτέλεσμα που θα κατέληγε αν εκτελούσε τους μετασχηματισμούς με αντίστροφη σειρά.

Ας εξετάσουμε, όμως, μια αρκετά χρήσιμη στην πράξη περίπτωση που είναι η περιστροφή γύρω από τυχαίο άξονα. Έστω ότι έχουμε το διάνυσμα p, το οποίο θέλουμε να περιστρέψουμε γύρω από το μοναδιαίο διάνυσμα (άξονα) v, όπως απεικονίζεται στην παρακάτω εικόνα:

Εικόνα 3.10. Το διάνυσμα p περιστρέφεται γύρω από το διάνυσμα v κατά γωνία θ και καταλήγει στο p’.

Το διάνυσμα p μπορεί να αποσυντεθεί σε δύο συνιστώσες: την p₁ παράλληλη με το v και την κάθετη σε αυτό p₂.

Εικόνα 3.11. Το διάνυσμα p μπορεί να αποσυντεθεί στην παράλληλη ως προς το v συνιστώσα p₁ και στην κάθετη p₂

Δεδομένου ότι το v είναι μοναδιαίο, οι δύο αυτές συνιστώσες προκύπτουν από τις παρακάτω σχέσεις:

p_{1} = (p \cdot v) v p_{2} = p - (p \cdot v) v

{Εξ. 3.43}

Τώρα είναι προφανές ότι η παράλληλη συνιστώσα δεν περιστρέφεται, οπότε το πρόβλημα περιορίζεται στον υπολογισμό της περιστροφής του p₂ γύρω από το v. Στη συνέχεια το αποτέλεσμα θα προστεθεί στο p₁. Πώς, όμως, μπορούμε να υπολογίσουμε την περιστροφή αυτή; Όπως απεικονίζεται και στο παρακάτω σχήμα, η περιστροφή του p₂γίνεται σε ένα επίπεδο κάθετο στο v.

Εικόνα 3.12. Η περιστροφή του p₂ γίνεται σε επίπεδο κάθετο στο v. Ο υπολογισμός του διανύσματος w το οποίο βρίσκεται πάνω στο επίπεδο και είναι κάθετο στο p_2,βοηθάει στον τριγωνομετρικό υπολογισμό της περιστροφής.

Εάν γνωρίζαμε το διάνυσμα w του παρακάτω σχήματος, τότε θα μπορούσαμε να χρησιμοποιήσουμε γνωστές τριγωνομετρικές σχέσεις, ώστε να υπολογίσουμε την περιστροφή:

p'_{2} = p_{2} \cos θ + w \sin θ

{Εξ. 3.44}

Με μια προσεκτικότερη ματιά στην Εικόνα 3.12, βλέπουμε ότι το διάνυσμα w που θέλουμε να υπολογίσουμε είναι κάθετο στο επίπεδο που σχηματίζεται από το p και το v και μπορεί να υπολογιστεί από το εξωτερικό τους γινόμενο:

w = v \times p

{Εξ. 3.45}

επίσης, παρατηρούμε ότι τα w και p₂ έχουν ίδιο πλάτος. Άρα το περιστραμμένο διάνυσμα προκύπτει από την παρακάτω σχέση:

p'_{2} = [p - (v \cdot p) v] \cos θ + (v \times p) \sin θ

{Εξ. 3.46}

Άρα τελικά το περιστραμμένο διάνυσμα είναι:

p' = p_{1} + p'_{2} = p \cos θ + (v \cdot p) v (1 - \cos θ) + (v \times p) \sin θ

{Εξ. 3.47}

και κάνοντας τις πράξεις προκύπτει ο παρακάτω πίνακας περιστροφής {Εξ. 3.48}:

$R_{V} (θ) = [\begin{matrix} c o s θ + (1 - c o s θ) v_{x}^{2} & (1 - c o s θ) v_{x} v_{y} - s i n θ \cdot v_{z} & (1 - c o s θ) v_{x} v_{z} + s i n θ \cdot v_{y} \\ (1 - c o s θ) v_{x} v_{y} + s i n θ \cdot v_{z} & c o s θ + (1 - c o s θ) v_{y}^{2} & (1 - c o s θ) v_{y} v_{z} - s i n θ \cdot v_{x} \\ (1 - c o s θ) v_{x} v_{z} - s i n θ \cdot v_{y} & (1 - c o s θ) v_{y} v_{z} + s i n θ \cdot v_{x} & c o s θ + (1 - c o s θ) v_{z}^{2} \end{matrix}]$

3.6. Προβολές

Στη γραμμική άλγεβρα ως προβολή πολλές φορές περιγράφεται η μεταφορά ενός διανυσματικού χώρου σε έναν άλλο μικρότερης διάστασης. Στα γραφικά και ειδικότερα στους μετασχηματισμούς ως προβολή εννοούμε την απόδοση ενός τρισδιάστατου αντικειμένου σε ένα επίπεδο, το οποίο και ονομάζουμε επίπεδο προβολής. Η διαδικασία της προβολής ενός τρισδιάστατου αντικειμένου σε ένα δισδιάστατο επίπεδο είναι σχετικά απλή αν και αποτελεί μία μόνο ειδική περίπτωση ενός ιδιαίτερα ενδιαφέροντος κλάδου των μαθηματικών ο οποίος είναι η προβολική γεωμετρία. Για να προβάλλουμε ένα σημείο σε ένα επίπεδο χρειαζόμαστε ένα κέντρο προβολής. Η ευθεία τώρα που ενώνει κάθε σημείο του τρισδιάστατου αντικειμένου με το κέντρο προβολής τέμνει το επίπεδο προβολής σε ένα σημείο, το οποίο είναι και το ίχνος του σημείου αυτού στο επίπεδο προβολής.

Εικόνα 3.13. Διαδικασία προβολής. Ένα σημείο p προβάλλεται στο επίπεδο προβολής.

Στα γραφικά ιδιαίτερο ενδιαφέρον παρουσιάζουν δύο προβολές: η προοπτική προβολή, κατά την οποία η απόσταση του κέντρου προβολής από το επίπεδο προβολής είναι πεπερασμένη και η ορθογραφική προβολή, η οποία αποτελεί εξιδανικευμένη περίπτωση όπου θεωρείται ότι η απόσταση αυτή είναι άπειρη.

3.6.1. Προοπτική Προβολή

Η προοπτική προβολή έχει πολλά κοινά στοιχεία με το ανθρώπινο σύστημα όρασης. Το κέντρο της προβολής αντιστοιχεί στην ίριδα, ενώ το επίπεδο προβολής αντιστοιχεί στον αμφιβληστροειδή χιτώνα.

Εικόνα 3.14. Προοπτική προβολή

Εάν υποθέσουμε τώρα, για χάρη απλότητας, ότι η αρχή των αξόνων αντιστοιχεί στο κέντρο προβολής και ότι το επίπεδο προβολής είναι παράλληλο με το επίπεδο xy και απέχει από αυτό απόσταση d προς τον αρνητικό ημιάξονα των z, τότε με αναφορά στην Εικόνα 3.14 έχουμε το εξής παράδειγμα.

Έστω το σημείο p₁, το οποίο βρίσκεται πάνω στο επίπεδο yz και το ίχνος του p₁’, πάνω στο επίπεδο προβολής. Έστω και το σημείο p₂, το οποίο βρίσκεται πάνω στον άξονα των z και το ίχνος του p₂’, πάνω στο επίπεδο προβολής. Παρατηρούμε ότι τα τρίγωνα Οp₁p₂ και Οp₁’p₂’ είναι όμοια. Άρα ισχύουν οι εξής σχέσεις:

\frac{p'_{1} p'_{2}}{O p'_{2}} = \frac{p_{1} p_{2}}{O p_{2}} \Rightarrow \frac{y'}{d} = \frac{y}{z} \Rightarrow y' = \frac{y \cdot d}{z}

{Εξ. 3.49}

Με παρόμοια ανάλυση για σημείο p₁ πάνω στο επίπεδο xz μπορεί εύκολα να εξαχθεί η παρακάτω σχέση:

x' = \frac{x \cdot d}{z}

{Εξ. 3.50}

ενώ για το z ισχύει πάντα ότι:

z' = d = \frac{z \cdot d}{z}

{Εξ. 3.51}

Πώς, όμως, μπορούμε να εκφράσουμε τις μη γραμμικές αυτές εξισώσεις της προοπτικής προβολής με τη μορφή ενός πίνακα M γραμμικού μετασχηματισμού; Για να το επιτύχουμε αυτό χρησιμοποιούμε την ομογενή συντεταγμένη. Παρατηρείστε ότι ο αριθμητής μπορεί εύκολα να περιγραφεί ως:

M = [\begin{matrix} d & 0 & 0 & 0 \\ 0 & d & 0 & 0 \\ 0 & 0 & d & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

{Εξ. 3.52}

Η εισαγωγή, όμως, του όρου του παρονομαστή παραμένει πρόβλημα. Εδώ πρέπει να θυμηθούμε μία ιδιότητα των ομογενών συντεταγμένων, κατά την οποία για να πάρουμε τις πραγματικές ευκλείδειες συντεταγμένες ενός σημείου με ομογενή συντεταγμένη w διάφορη του 1, πρέπει να διαιρέσουμε όλες τις συντεταγμένες με το w, έτσι ώστε η ομογενής συντεταγμένη να γίνει 1. Αντί να διαιρέσουμε κάθε x, y, z συντεταγμένη, αρκεί να πολλαπλασιάσουμε την ομογενή συντεταγμένη με το z. Έτσι, προκύπτει ο πίνακας προοπτικής προβολής:

M = [\begin{matrix} d & 0 & 0 & 0 \\ 0 & d & 0 & 0 \\ 0 & 0 & d & 0 \\ 0 & 0 & 1 & 0 \end{matrix}]

{Εξ. 3.53}

Οπότε έχουμε:

p' = M p = [\begin{matrix} d & 0 & 0 & 0 \\ 0 & d & 0 & 0 \\ 0 & 0 & d & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} d \cdot x \\ d \cdot y \\ d \cdot z \\ z \end{matrix}]

{Εξ. 3.54}

Για να εξάγουμε, όμως, τις ευκλείδειες συντεταγμένες, πρέπει να διαιρεθεί το αποτέλεσμα με την ομογενή συντεταγμένη:

p' = [\begin{matrix} d \cdot x \\ d \cdot y \\ d \cdot z \\ z \end{matrix}] / z = [\begin{matrix} \frac{d \cdot x}{z} \\ \frac{d \cdot y}{z} \\ d \\ 1 \end{matrix}]

{Εξ. 3.55}

Ένα σημαντικό χαρακτηριστικό της προοπτικής προβολής, σχετίζεται με τη σμίκρυνση των αντικειμένων τα οποία βρίσκονται μακριά από το κέντρο προβολής. Η πρακτική αυτή παρατήρηση κωδικοποιείται μαθηματικά στη διαίρεση με τη συντεταγμένη z στην παραπάνω σχέση.

3.6.2. Ορθογραφική Προβολή

Η ορθογραφική προβολή βασίζεται στην υπόθεση ότι η απόσταση μεταξύ του κέντρου και του επιπέδου προβολής είναι άπειρη. Πρακτικά, η ορθογραφική προβολή εφαρμόζεται όταν οι διαστάσεις ενός προβλήματος είναι αμελητέες σε σχέση με την απόσταση του επιπέδου προβολής από το κέντρο προβολής. Αυτή η υπόθεση που απεικονίζεται στην παρακάτω Εικόνα 3.15 οδηγεί σε μία πολύ χρήσιμη μαθηματική απλοποίηση, η οποία είναι η εξαφάνιση της προοπτικής σμίκρυνσης και της διαίρεσης με τη συντεταγμένη του βάθους z.

Εικόνα 3.15. Ορθογραφική προβολή με το επίπεδο προβολής στο z=0

Οπότε, όπως είναι προφανές από την παραπάνω εικόνα, οι συντεταγμένες x και y παραμένουν αμετάβλητες, ενώ η συντεταγμένη z παύει να έχει νόημα εφόσον όποια τιμή και αν πάρει το αποτέλεσμα της προβολής δεν αλλάζει. Η ορθογραφική προβολή για z=0 μπορεί να περιγραφεί από τον παρακάτω πίνακα:

Άρα και η ορθογραφική προβολή ενός σημείου περιγράφεται από την παρακάτω εξίσωση.

p' = M p = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} x \\ y \\ 0 \\ 1 \end{matrix}]

{Εξ. 3.56}

Η ορθογραφική προβολή χρησιμοποιείται κατά κόρον όπου οι διαστάσεις του προβλήματος μπορούν να θεωρηθούν αμελητέες σε σχέση με την απόσταση του επιπέδου προβολής από το κέντρο προβολής. Επίσης χρησιμοποιείται και σε περιπτώσεις όπου η προοπτική σμίκρυνση είναι περισσότερο ανεπιθύμητη παρά στοιχείο ρεαλισμού, όπως στην περίπτωση των προσόψεων, κατόψεων και πλάγιων όψεων συστημάτων σχεδίασης με υπολογιστή CAD (Computer Aided Design). Όπως φαίνεται στην Εικόνα 3.6, η τρισδιάστατη όψη συντίθεται βάσει της προοπτικής προβολής, ενώ οι άλλες τρεις πλάγιες όψεις του σχεδίου συντίθενται βάσει της ορθογραφικής προβολής. Στην Εικόνα 3.17 παρουσιάζονται δύο προβολές της ίδιας σκηνής: Μία προοπτική (πάνω-αριστερά) και μία ορθογραφική (πάνω-δεξιά), ενώ παρατίθεται και μία φωτορεαλιστική απόδοση (κάτω).

Εικόνα 3.16. Στιγμιότυπο από το πρόγραμμα CAD γραφικών Blender. Για τη 3Δ προβολή (πάνω δεξιά) χρησιμοποιείται, συνήθως, προοπτική προβολή, ενώ για τις πλάγιες όψεις ορθογραφική.

Εικόνα 3.17. Προβολές της ίδιας σκηνής: Μια προοπτική (πάνω-αριστερά), μία ορθογραφική (κάτω) και μία φωτορεαλιστική απόδοση (πάνω-δεξιά)

3.7. Προτεινόμενες Ασκήσεις και Προβλήματα

Άσκηση 1)

Υπολογίστε του πίνακες περιστροφής, οι οποίοι εκτελούν μία περιστροφή 60 μοιρών γύρω από τους άξονες x- y-z-.

Άσκηση 2)

Έστω σημείο ένα σημείο s στο χώρο και ένα επίπεδο Π με κάθετο διάνυσμα n. Υπολογίστε τον 3Δ πίνακα μετασχηματισμού που εκτελεί καθρεπτισμό του σημείου s ως προς το επίπεδο Π.

Άσκηση 3)

Είναι πολύ χρήσιμο να μπορεί κανείς να αναγνωρίζει το μετασχηματισμό που εκτελεί ένας πίνακας απλά κοιτάζοντάς τον. Για παράδειγμα ένας 3x3 πίνακας ομογενούς μετατόπισης στις δύο διαστάσεις έχει την τελευταία γραμμή [0 0 1] και ο άνω-αριστερά 2x2 υποπίνακας είναι ο μοναδιαίος. Έστω ο ίδιος 3x3 πίνακας μετασχηματισμού σε ομογενείς συντεταγμένες:

α) Πώς μπορούμε να διακρίνουμε εάν ο μετασχηματισμός είναι γραμμικός;

β) Πώς μπορούμε να διακρίνουμε εάν αφορά περιστροφή γύρω από την αρχή των αξόνων;

γ) Πώς μπορούμε να διακρίνουμε εάν αφορά ομοιόμορφη κλιμάκωση;

Άσκηση 4)

Υπολογίστε το σύνθετο πίνακα μετασχηματισμού Μ₁ ο οποίος προκύπτει από περιστροφή πρώτα γύρω από τον άξονα z- και στη συνέχεια γύρω από τον άξονα y-. Στη συνέχεια υπολογίστε το σύνθετο πίνακα μετασχηματισμού Μ₂ που εκτελεί τις ίδιες περιστροφές με αντίθετη φορά. Επιβεβαιώστε ότι οι δύο πίνακες δεν ταυτίζονται.

3.8. Αναφορές

Angel E. (2002). Interactive Computer Graphics (3rd ed.). Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA.
J. Blinn. 1996. A Trip Down the Graphics Pipeline. Morgan Kaufmann, 1996
Foley, J.D., van Dam Α., Feiner S.K., Hughes J.F. (1990). Computer Graphics: Principles and Practice (2nd Ed.). Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA.
Lengyel E. (2011). Mathematics for 3D Game Programming and Computer Graphics, Third Edition (3rd ed.). Course Technology Press, Boston, MA, United States.
Θεοχάρης Θ., Μπέμ Α., Καραμπάση Α., Παπαϊωάννου Γ., Πλατής Ν. (1999). Γραφικά: Αρχές και Αλγόριθμοι, Εκδόσεις Συμμετρία, Αθήνα.

Κουίζ αυτοαξιολόγησης

Περιεχόμενα