Παρατήρηση 10.1
Και πάλι, δεν υπάρχει, στον Ορισμό 10.3, τίποτα το μαγικό με το σύνολο
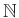 και θα μπορούσαμε στη θέση του να έχουμε, π.χ. το σύνολο
και θα μπορούσαμε στη θέση του να έχουμε, π.χ. το σύνολο 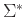 ,
όπου
,
όπου 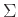 ένα πεπερασμένο αλφάβητο.
ένα πεπερασμένο αλφάβητο.
Είναι σχεδόν άμεσο ότι κάθε αναδρομικό σύνολο είναι και α.α.
Πράγματι, αν
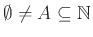 είναι αναδρομικό τότε υπάρχει πρόγραμμα
είναι αναδρομικό τότε υπάρχει πρόγραμμα
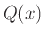 τέτοιο ώστε
τέτοιο ώστε
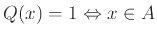 .
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του
.
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του  .
.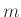 είναι, π.χ., το
μικρότερο στοιχείο του
είναι, π.χ., το
μικρότερο στοιχείο του  ):
):
def P(x):
if Q(x):
return x
else:
return m
Άσκηση 10.3
Αν
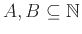 είναι α.α. σύνολα δείξτε ότι το ίδιο
ισχύει και για τα σύνολα
είναι α.α. σύνολα δείξτε ότι το ίδιο
ισχύει και για τα σύνολα
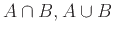 .
.
Από την άλλη μεριά είναι εύκολο να κατασκευάσουμε α.α. σύνολα που δεν
είναι αναδρομικά. Για παράδειγμα, το σύνολο
δεν είναι αναδρομικό (αν ήταν τότε το πρόβλημα του τερματισμού
θα ήταν υπολογίσιμο, ενώ έχουμε δείξει ότι δεν είναι) αλλά είναι α.α.
Για να δούμε αυτό τον τελευταίο ισχυρισμό κάνουμε το εξής.
Χρειαζόμαστε ένα πρόγραμμα που να απαριθμεί τα
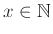 για τα οποία
το πρόγραμμα
για τα οποία
το πρόγραμμα 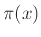 τερματίζει. Ισοδύναμα, φτιάχνουμε ένα πρόγραμμα
που λειτουργεί επ' άπειρον και τυπώνει συνέχεια στην έξοδό του στοιχεία
του
τερματίζει. Ισοδύναμα, φτιάχνουμε ένα πρόγραμμα
που λειτουργεί επ' άπειρον και τυπώνει συνέχεια στην έξοδό του στοιχεία
του  , χωρίς να παραλείψει κανένα.
Το πρόγραμμα αυτό
, χωρίς να παραλείψει κανένα.
Το πρόγραμμα αυτό
- Βήμα 1: Πρώτα τρέχει (προσομοιώνει) το πρόγραμμα
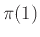 για 1 βήμα.
για 1 βήμα.
- Βήμα 2: Έπειτα τρέχει (προσομοιώνει) τα προγράμματα
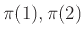 για 2 βήματα το καθένα
για 2 βήματα το καθένα
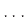
- Βήμα
 : Τρέχει τα προγράμματα
: Τρέχει τα προγράμματα
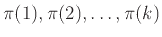 για
για  βήματα το καθένα,
βήματα το καθένα,
- Συνεχίζει έτσι επ' άπειρον.
Στο τέλος του βήματος  το πρόγραμμά μας ελέγχει ποια από τα προγράμματα
το πρόγραμμά μας ελέγχει ποια από τα προγράμματα
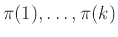 τελείωσαν μέσα στα πρώτα
τελείωσαν μέσα στα πρώτα  τους βήματα, και τυπώνει
τα αντίστοιχα
τους βήματα, και τυπώνει
τα αντίστοιχα 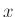 για αυτά που τελείωσαν στην έξοδό του.
Είναι έτσι φανερό ότι κάθε
για αυτά που τελείωσαν στην έξοδό του.
Είναι έτσι φανερό ότι κάθε 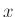 για το οποίο
για το οποίο
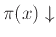 θα εμφανιστεί
στην έξοδο του προγράμματός μας, και ότι σε αυτή την έξοδο εμφανίζονται
μόνο τέτοια
θα εμφανιστεί
στην έξοδο του προγράμματός μας, και ότι σε αυτή την έξοδο εμφανίζονται
μόνο τέτοια 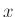 (δηλ. στοιχεία του
(δηλ. στοιχεία του  ).
Αν
).
Αν 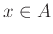 και το πρόγραμμα
και το πρόγραμμα 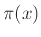 τερματίζει μετά από
τερματίζει μετά από 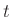 βήματα
τότε ο αριθμός
βήματα
τότε ο αριθμός 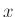 εμφανίζεται για πρώτη φορά στην έξοδο του προγράμματός
μας μετά το βήμα υπ' αριθμόν
εμφανίζεται για πρώτη φορά στην έξοδο του προγράμματός
μας μετά το βήμα υπ' αριθμόν
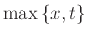 , και εμφανίζεται και σε όλα
τα μεταγενέστερα βήματα.
, και εμφανίζεται και σε όλα
τα μεταγενέστερα βήματα.
Έχουμε λοιπόν δείξει:
Θεώρημα 10.3
Κάθε αναδρομικό σύνολο είναι αναδρομικά απαριθμήσιμο αλλά το αντίστροφο
δεν ισχύει.
Η ιεραρχία των γλωσσών τώρα γίνεται
(κανονικές γλώσσες) 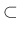 (context free γλώσσες)
(context free γλώσσες) 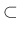 (αναδρομικές γλώσσες)
(αναδρομικές γλώσσες)
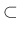 (α.α. γλώσσες)
(α.α. γλώσσες)
και όλοι οι εγκλεισμοί είναι γνήσιοι.
Η σχέση αναδρομικών και α.α. συνόλων φαίνεται πιο καθαρά στα επόμενα
δύο θεωρήματα.
Θεώρημα 10.4
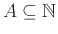 είναι αναδρομικό αν και μόνο αν τα
είναι αναδρομικό αν και μόνο αν τα 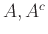 είναι και
τα δύο α.α.
είναι και
τα δύο α.α.
Θεώρημα 10.5
Ένα σύνολο
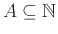 είναι α.α. αν και μόνο αν υπάρχει πρόγραμμα
είναι α.α. αν και μόνο αν υπάρχει πρόγραμμα
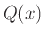 τέτοιο ώστε
τέτοιο ώστε
- Αν
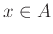 τότε
τότε 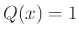 , και
, και
- Αν
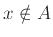 τότε
τότε 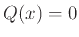 ή
ή
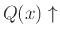 .
.
Το πρόγραμμα 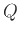 στο θεώρημα λέει την αλήθεια για το αν
στο θεώρημα λέει την αλήθεια για το αν 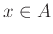 , αν τελειώνει,
μπορεί όμως και να τρέχει επ' άπειρον (αλλά αυτό μπορεί να συμβαίνει μόνο
αν
, αν τελειώνει,
μπορεί όμως και να τρέχει επ' άπειρον (αλλά αυτό μπορεί να συμβαίνει μόνο
αν 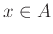 .
Παρατηρήστε ότι υπάρχει ασυμμετρία στις δύο περιπτώσεις
.
Παρατηρήστε ότι υπάρχει ασυμμετρία στις δύο περιπτώσεις 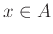 και
και
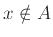 ,
και αυτή η ασυμμετρία εκδηλώνεται και με το ότι υπάρχουν α.α. σύνολα που τα
συμπληρώματά τους δεν είναι α.α.
,
και αυτή η ασυμμετρία εκδηλώνεται και με το ότι υπάρχουν α.α. σύνολα που τα
συμπληρώματά τους δεν είναι α.α.
Απόδειξη.
Έστω ότι το πρόγραμμα
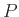
απαριθμεί τα στοιχεία του

:
Ορίζουμε το πρόγραμμα
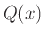
ως εξής:
def Q(x):
i=1
while True:
if P(i)==x:
return 1
i = i+1
Το πρόγραμμα 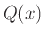 επιστρέφει 1 αν και μόνο αν το
επιστρέφει 1 αν και μόνο αν το 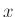 εμφανιστεί στη λίστα
των τιμών του
εμφανιστεί στη λίστα
των τιμών του 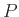 , αλλιώς τρέχει επ' άπειρον.
, αλλιώς τρέχει επ' άπειρον.
Η άλλη κατεύθυνση του Θεωρήματος 10.5 αφήνεται ως άσκηση.

Άσκηση 10.4
Αποδείξτε την κατεύθυνση του Θεωρήματος 10.5
που λείπει από την απόδειξη που δόθηκε παραπάνω.
Mihalis Kolountzakis
2015-11-28
![]() είναι αναδρομικό τότε υπάρχει πρόγραμμα
είναι αναδρομικό τότε υπάρχει πρόγραμμα
![]() τέτοιο ώστε
τέτοιο ώστε
![]() .
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του
.
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του ![]() .
.![]() είναι, π.χ., το
μικρότερο στοιχείο του
είναι, π.χ., το
μικρότερο στοιχείο του ![]() ):
):
(context free γλώσσες)
(αναδρομικές γλώσσες)
(α.α. γλώσσες)
![]() απλούστατα παράγει όλους τους αριθμούς
απλούστατα παράγει όλους τους αριθμούς
![]() και μόλις εμφανιστεί το
και μόλις εμφανιστεί το ![]() επιστρέφει 0 ή 1 ανάλογα με το αν το
επιστρέφει 0 ή 1 ανάλογα με το αν το ![]() εμφανίστηκε στην έξοδο του
εμφανίστηκε στην έξοδο του
![]() ή του
ή του ![]() .
Είναι σίγουρο ότι το
.
Είναι σίγουρο ότι το ![]() κάποτε θα εμφανιστεί (μια και είτε θα ανήκει στο
κάποτε θα εμφανιστεί (μια και είτε θα ανήκει στο
![]() είτε στο
είτε στο ![]() ) και άρα για κάθε
) και άρα για κάθε ![]() το πρόγραμμα
το πρόγραμμα ![]() τερματίζει.
τερματίζει.
![]()
![]() επιστρέφει 1 αν και μόνο αν το
επιστρέφει 1 αν και μόνο αν το ![]() εμφανιστεί στη λίστα
των τιμών του
εμφανιστεί στη λίστα
των τιμών του ![]() , αλλιώς τρέχει επ' άπειρον.
, αλλιώς τρέχει επ' άπειρον.
![]()