Όπως ακριβώς οι κανονικές γλώσσες έχουν αντίστοιχες μηχανές, τα DFA,
ή τα NFA ή τα 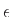 -NFA, που αναγνωρίζουν ακριβώς το σύνολο
των κανονικών γλωσσών, έτσι υπάρχει και μια μηχανή, το αυτόματο με στοίβα,
ή Push Down Automaton (PDA) που έχει την ιδότητα ότι μια γλώσσα
-NFA, που αναγνωρίζουν ακριβώς το σύνολο
των κανονικών γλωσσών, έτσι υπάρχει και μια μηχανή, το αυτόματο με στοίβα,
ή Push Down Automaton (PDA) που έχει την ιδότητα ότι μια γλώσσα 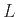 είναι context free αν και μόνο αν υπάρχει PDA που την αναγνωρίζει.
Δε θα δείξουμε αυτή την ισοδυναμία εδώ (όπως είχαμε κάνει για τις κανονικές
γλώσσες και τα πεπερασμένα αυτόματα).
είναι context free αν και μόνο αν υπάρχει PDA που την αναγνωρίζει.
Δε θα δείξουμε αυτή την ισοδυναμία εδώ (όπως είχαμε κάνει για τις κανονικές
γλώσσες και τα πεπερασμένα αυτόματα).
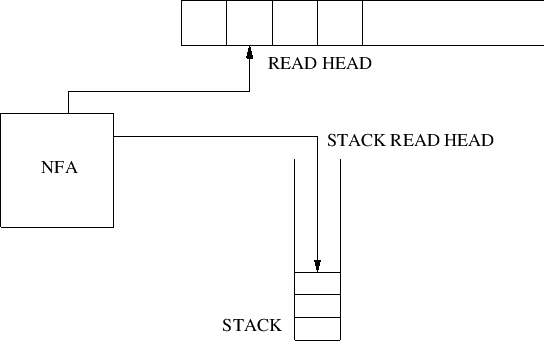
Σχήμα
9.1: Ένα αυτόματο με στοίβα
Ένα PDA (Σχήμα 9.1)
αποτελείται από τρία μέρη
- Ένα NFA που το βλέπουμε σα «μονάδα ελέγχου» της μηχανής.
Είναι σημαντικό εδώ να τονίσουμε
ότι δε μπορούμε εδώ να αντικαταστήσουμε το NFA με DFA - τα
αυτόματα με στοίβα είναι μη ντετερμινιστικές μηχανές.
-
Μια ταινία ανάγνωσης (read tape) που διαβάζεται από τον έλεγχο (NFA)
με μια κεφαλή ανάγνωσης (read head) η οποία αρχίζει από τα αριστερά
της ταινίας ανάγνωσης και κινείται μόνο προς τα δεξιά, και το πολύ κατά ένα
σε κάθε βήμα (κύκλο) της μηχανής. Η προς αναγνώριση λέξη πρέπει να τοποθετηθεί
εξ αρχής πάνω σε αυτή την ταινία από τον «χρήστη» της μηχανής.
-
Μια στοίβα (stack).
Η στοίβα είναι μια απεριόριστη ποσότητα μνήμης
την οποία όμως μπορούμε να διαχειριστούμε με πολύ περιορισμένο τρόπο.
Φανταζόμαστε τη στοίβα σα μια (αρχικά κενή) στήλη από θέσεις μνήμης, που
αρχίζει από το επίπεδό μας και εκτείνεται απείρως προς τα πάνω.
Σε κάθε θέση μνήμης μπορούμε να γράψουμε ένα οποιοδήποτε από τα γράμματα
του αλφαβήτου μας ή ένα πεπερασμένο αριθμό από άλλα ειδικά σύμβολα που
ενδεχομένως μας διευκολύνουν στον «προγραμματισμό» του PDA.
Στη στήλη αυτή μπορούμε να κάνουμε τις εξής τρεις πράξεις μόνο:
- Μπορούμε να δούμε τα περιεχόμενα της πρώτης (από πάνω προς τα κάτω)
θέσης μνήμης που είναι μη κενή. Αν η στοίβα είναι κενή μπορούμε να το διαπιστώσουμε
αυτό.
- Μπορούμε να προσθέσουμε κάτι στη στοίβα αλλά μόνο ακριβώς στη θέση
μνήμης πάνω από την πρώτη (από πάνω προς τα κάτω) γεμάτη θέση μνήμης.
Η πράξη αυτή αυξάνει λοιπόν το ύψος της στοίβας κατά 1.
- Μπορούμε να διαγράψουμε την πιο πάνω θέση μνήμης (αν η στοίβα είναι κενή
αυτή η πράξη δεν έχει κανένα αποτέλεσμα). Η πράξη αυτή ελαττώνει το
ύψος της στοίβας κατά ένα αν η στοίβα δεν ήταν κενή.
Το NFA του αυτομάτου διαβάζει πάλι τα γράμματα της προς αναγνώριση
λέξης ένα προς ένα, από αριστερά προς τα δεξιά, χωρίς και πάλι τη δυνατότητα
να γυρίσει πίσω προς τα πίσω και να ξαναδιαβάσει την αρχή της λέξης.
Και πάλι σε κάθε βήμα το NFA έχει τη δυνατότητα να εκτελέσει
μια κίνηση ανάμεσα σε διάφορες δυνατές κινήσεις. Μια λέξη αναγνωρίζεται
από το PDA αν κάποια επιλογή κινήσεων του NFA μπορεί να
οδηγήσει σε αποδοχή της λέξης (το οποίο συμβαίνει αν στο τέλος το
NFA είναι σε τελική κατάσταση).
Η σύνδεση του NFA με τη στοίβα γίνεται ως εξής: σε κάθε μετάβαση το
NFA δεν επιλέγει το σύνολο των δυνατών επομένων καταστάσεων με κριτήριο
μόνο το σε ποια κατάσταση βρίσκεται αυτό αλλά κοιτώντας ταυτόχρονα
και ποιο είναι το περιεχόμενο της πάνω θέσης μνήμης της στοίβας (η μόνη θέση
μνήμης που μπορεί άλλωστε να δει). Επίσης σε κάθε μετάβαση το
NFA εκτελεί ενδεχομένως και μια από τις τρεις επιτρεπτές πράξεις στη
στοίβα (διαβάζει την κορυφή της, προσθέτει κάτι στην κορυφή της, πετάει
την πάνω θέση μνήμης χαμηλώνοντας την κορυφή της στοίβας κατά ένα, ή δεν
κάνει τίποτα στη στοίβα).
Το μοντέλο του PDA είναι λειτουργικά ισοδύναμο με προγραμματισμό
σε μια συνηθισμένη γλώσσα προγραμματισμού (π.χ. στην python)
με τους εξής περιορισμούς και προσθήκες.
- Η μνήμη (εκτός της στοίβας) που χρησιμοποιεί το πρόγραμμά μας πρέπει να είναι συνολικά πεπερασμένη
και γνωστή εξ' αρχής, ανεξάρτητα από το ποιο θα είναι το input (η προς
αναγνώριση λέξη). Στην πράξη, αυτό το εξασφαλίζουμε δηλώνοντας μερικές
μεταβλητές ακέραιου τύπου μόνο και λαμβάνοντας υπόψιν
ότι κάθε τέτοια μεταβλητή δε μπορεί να μεγαλώσει απεριόριστα, έχει δηλ. συγκεκριμένο
αριθμό από bits (δυαδικά ψηφία) που αντιστοιχούν σε αυτή.
- Η πρόσβαση στο input γίνεται μέσω της συνάρτησης INP()
η οποία κάθε φορά που καλείται επιστρέφει και το επόμενο γράμμα της λέξης
που εξετάζουμε. Όταν έχει διαβάσει όλα τα γράμματα επιστρέφει από κει και πέρα
την ειδική τιμή -1.
- Υπάρχουν ακόμη άλλες τρεις «συναρτήσεις βιβλιοθήκης» με τις οποίες γίνεται
ο χειρισμός της στοίβας, και μια συνάρτηση ακόμη με την οποία μπαίνει μέσα
στη γλώσσα ο μη ντετερμινισμός που είναι απαραίτητος στο PDA.
Οι συναρτήσεις για τη στοίβα είναι οι εξής:
| READ() |
Επιστρέφει τα περιεχόμενα της πάνω θέσης μνήμης της
στοίβας ή -1 αν η στοίβα είναι άδεια. |
| POP() |
αδειάζει μια θέση μνήμης από τη στοίβα ή δεν κάνει τίποτα αν
η στοίβα είναι ήδη άδεια |
| PUSH(x) |
Γράφει τον αριθμό x στην κορυφή της στοίβας, σε μια
νέα θέση μνήμης |
- Η συνάρτηση NF μέσω της οποίας κωδικοποιείται η μη ντετερμινιστική συμπεριφορά
περιγράφεται στην επόμενη παράγραφο.
Μη ντετερμινιστικά «προγράμματα»
Γενικά ο μηχανισμός του μη ντετερμινισμού χρησιμοποιείται σε προβλήματα
αποφάσεων, σε ερωτήματα δηλαδή που φιλοδοξούμε να λύσουμε υπολογιστικά
και τα οποία επιδέχονται ΝΑΙ ή ΟΧΙ απάντηση, όπως ακριβώς είναι
και το πρόβλημα που μας ενδιαφέρει εδώ, να αποφασίζουμε δηλ. αν μια λέξη
που μας δίνεται ανήκει σε μια γλώσσα 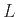 ή όχι.
ή όχι.
Η συνάρτηση μέσω της οποίας «υλοποιείται» ο μη ντετερμινισμός είναι η
NF(x) η οποία επιστρέφει μη ντετερμινιστικά μια
από τις επιλογές
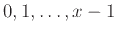 .
Το νόημα της συνάρτησης αυτής είναι
ότι εμείς δεν έχουμε κανένα έλεγχο στο ποια από τις δυνατές επιλογές αυτή
επιλέγει, αλλά πρέπει να γράψουμε το πρόγραμμά μας με τέτοιo τρόπο ώστε
αν αυτή η συνάρτηση επιστρέψει κατά τις κλήσεις της τις κατάλληλες
επιλογές τότε να κάνουμε τη λέξη δεκτή, αν αυτή είναι μέσα στη γλώσσα.
Αλλά, δεν πρέπει να σε καμία
περίπτωση να κάνουμε δεκτή μια λέξη που δεν ανήκει στη γλώσσα
όποιες τιμές κι αν επιστρέψει η NF.
.
Το νόημα της συνάρτησης αυτής είναι
ότι εμείς δεν έχουμε κανένα έλεγχο στο ποια από τις δυνατές επιλογές αυτή
επιλέγει, αλλά πρέπει να γράψουμε το πρόγραμμά μας με τέτοιo τρόπο ώστε
αν αυτή η συνάρτηση επιστρέψει κατά τις κλήσεις της τις κατάλληλες
επιλογές τότε να κάνουμε τη λέξη δεκτή, αν αυτή είναι μέσα στη γλώσσα.
Αλλά, δεν πρέπει να σε καμία
περίπτωση να κάνουμε δεκτή μια λέξη που δεν ανήκει στη γλώσσα
όποιες τιμές κι αν επιστρέψει η NF.
Για να γίνει κατανοητός ο τρόπος χρήσης της NF
δείχνουμε παρακάτω μια συνάρτηση σε python η οποία παίρνει δύο
ορίσματα number και vector και επιστρέφει
True αν ο ακέραιος number περιέχεται στον πίνακα (λίστα) vector
(ο οποίος έχει 1000 στοιχεία, τα vector[0], ..., vector[999]) και
False αν δεν περιέχεται.
def NumberInVector(number, vector):
location = NF(1000)
if number == vector[location]:
return True
else:
return False
Πρέπει εδώ να ξεκαθαρίσουμε ότι η συνάρτηση NumberInVector
λύνει το πρόβλημα που θέλουμε υπό την εξής έννοια:
- Αν ο αριθμός number είναι μέσα στον πίνακα vector
τότε υπάρχει τρόπος να απαντήσει η NF ώστε ο αλγόριθμός μας
να δώσει τη σωστή απάντηση, δηλ. True.
- Αν ο αριθμός number δεν είναι μέσα στον πίνακα vector
τότε, ό,τι και να απαντήσει η NF, ο αλγόριθμός μας δεν υπάρχει
περίπτωση να κάνει λάθος (αφού ελέγχει αν όντως βρίσκεται ο number
στη θέση vector[location] πριν απαντήσει) και απαντάει
πάντα False.
Αν δεν είχαμε στη διάθεσή μας τη συνάρτηση NF θα είμασταν
αναγκασμένοι, λίγο-πολύ, να κάνουμε χίλιους ελέγχους για να διαπιστώσουμε
αν ο δεδομένος αριθμός είναι μέσα στον πίνακα ή όχι.
Παρατηρήστε ότι τώρα δεν υπάρχει ανακύκλωση κανενός είδους μέσα στη
συνάρτηση και ότι η απάντηση βρίσκεται σε σταθερό χρόνο!
Ο αλγόριθμος της συνάρτησης NumberInVector «μαντεύει»
τη θέση στην οποία βρίσκεται στο vector ο αριθμός
και απλά ελέγχει μετά αν είναι όντως έτσι πριν απαντήσει True ή False,
ώστε να αποφύγει να κάνει λάθος στην περίπτωση που ο αριθμός δεν είναι
μέσα.
Ο αλγόριθμος αυτός δηλ. δεν υπάρχει περίπτωση να απαντήσει True ενώ η σωστή απάντηση
είναι False, αλλά μπορεί κάλλιστα να απαντήσει False όταν η σωστή απάντηση είναι
True.
Αυτή η ασυμμετρία είναι πολύ χαρακτηριστική στους μη ντετερμινιστικούς
αλγορίθμους.
Πρέπει να είναι φανερό με αυτό το παράδειγμα, ότι μη ντετερμινιστικοί
αλγόριθμοι δεν μπορούν να υλοποιηθούν. Είναι απλά ένα χρήσιμο θεωρητικό
κατασκεύασμα.
Mihalis Kolountzakis
2015-11-28
![]() -NFA, που αναγνωρίζουν ακριβώς το σύνολο
των κανονικών γλωσσών, έτσι υπάρχει και μια μηχανή, το αυτόματο με στοίβα,
ή Push Down Automaton (PDA) που έχει την ιδότητα ότι μια γλώσσα
-NFA, που αναγνωρίζουν ακριβώς το σύνολο
των κανονικών γλωσσών, έτσι υπάρχει και μια μηχανή, το αυτόματο με στοίβα,
ή Push Down Automaton (PDA) που έχει την ιδότητα ότι μια γλώσσα ![]() είναι context free αν και μόνο αν υπάρχει PDA που την αναγνωρίζει.
Δε θα δείξουμε αυτή την ισοδυναμία εδώ (όπως είχαμε κάνει για τις κανονικές
γλώσσες και τα πεπερασμένα αυτόματα).
είναι context free αν και μόνο αν υπάρχει PDA που την αναγνωρίζει.
Δε θα δείξουμε αυτή την ισοδυναμία εδώ (όπως είχαμε κάνει για τις κανονικές
γλώσσες και τα πεπερασμένα αυτόματα).
![]() ή όχι.
ή όχι.
![]() .
Το νόημα της συνάρτησης αυτής είναι
ότι εμείς δεν έχουμε κανένα έλεγχο στο ποια από τις δυνατές επιλογές αυτή
επιλέγει, αλλά πρέπει να γράψουμε το πρόγραμμά μας με τέτοιo τρόπο ώστε
αν αυτή η συνάρτηση επιστρέψει κατά τις κλήσεις της τις κατάλληλες
επιλογές τότε να κάνουμε τη λέξη δεκτή, αν αυτή είναι μέσα στη γλώσσα.
Αλλά, δεν πρέπει να σε καμία
περίπτωση να κάνουμε δεκτή μια λέξη που δεν ανήκει στη γλώσσα
όποιες τιμές κι αν επιστρέψει η NF.
.
Το νόημα της συνάρτησης αυτής είναι
ότι εμείς δεν έχουμε κανένα έλεγχο στο ποια από τις δυνατές επιλογές αυτή
επιλέγει, αλλά πρέπει να γράψουμε το πρόγραμμά μας με τέτοιo τρόπο ώστε
αν αυτή η συνάρτηση επιστρέψει κατά τις κλήσεις της τις κατάλληλες
επιλογές τότε να κάνουμε τη λέξη δεκτή, αν αυτή είναι μέσα στη γλώσσα.
Αλλά, δεν πρέπει να σε καμία
περίπτωση να κάνουμε δεκτή μια λέξη που δεν ανήκει στη γλώσσα
όποιες τιμές κι αν επιστρέψει η NF.