Από τον ορισμό των κανονικών εκφράσεων και των γλωσσών είναι
φανερό ότι αν 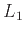 και
και 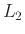 είναι κανονικές γλώσσες τότε
κανονική είναι και η
είναι κανονικές γλώσσες τότε
κανονική είναι και η
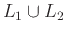 όπως και η γλώσσα
όπως και η γλώσσα 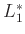 .
Δεν είναι όμως καθόλου προφανές από τον ορισμό των κανονικών εκφράσεων
το αν η συμπληρωματική γλώσσα
.
Δεν είναι όμως καθόλου προφανές από τον ορισμό των κανονικών εκφράσεων
το αν η συμπληρωματική γλώσσα
είναι κανονική.
Γίνεται όμως και αυτό φανερό αν χρησιμοποιήσουμε
το Θεώρημα 7.3
που λέει ότι μια γλώσσα είναι κανονική αν και μόνο
αν υπάρχει ένα DFA που την αναγνωρίζει.
Έστω λοιπόν ότι το DFA 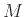 αναγνωρίζει τη γλώσσα
αναγνωρίζει τη γλώσσα 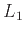 .
Φτιάνχουμε ένα DFA
.
Φτιάνχουμε ένα DFA 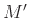 από το
από το 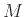 κρατώντας τις ίδιες καταστάσεις, αλφάβητο, αρχική κατάσταση και ακμές του
κρατώντας τις ίδιες καταστάσεις, αλφάβητο, αρχική κατάσταση και ακμές του 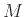 αλλά κάνουμε όλες τις τελικές καταστάσεις του
αλλά κάνουμε όλες τις τελικές καταστάσεις του 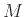 μη τελικές και όλες τις
μη τελικές καταστάσεις του
μη τελικές και όλες τις
μη τελικές καταστάσεις του 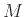 τις κάνουμε τελικές στο
τις κάνουμε τελικές στο 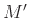 .
(Εδώ πρέπει να είμαστε λίγο προσεκτικοί και να δουλεύουμε στο μορφή
του
.
(Εδώ πρέπει να είμαστε λίγο προσεκτικοί και να δουλεύουμε στο μορφή
του 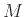 που δε χρησιμοποιεί συντομογραφία, αλλά που ικανοποιεί την αρχική
απαίτηση για DFA, ότι δηλ. για κάθε κατάσταση και για κάθε γράμμα
του αλφαβήτου υπάρχει ακριβώς μια ακμή.)
Είναι φανερό τώρα ότι μια λέξη γίνεται δεκτή στο
που δε χρησιμοποιεί συντομογραφία, αλλά που ικανοποιεί την αρχική
απαίτηση για DFA, ότι δηλ. για κάθε κατάσταση και για κάθε γράμμα
του αλφαβήτου υπάρχει ακριβώς μια ακμή.)
Είναι φανερό τώρα ότι μια λέξη γίνεται δεκτή στο 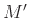 αν και μόνο αν δε γίνεται
δεκτή στο
αν και μόνο αν δε γίνεται
δεκτή στο 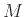 , άρα το
, άρα το 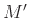 είναι ένα DFA για τη γλώσσα
είναι ένα DFA για τη γλώσσα 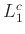 .
.
Είναι τώρα εύκολο να δείξουμε ότι και η γλώσσα
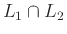 είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, και
είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, και
και από αυτά που είπαμε προηγουμένως προκύπτει ο ισχυρισμός.
Έχοντας μια αντικατάσταση
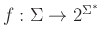 μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του
μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του 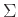 σε λέξεις του
σε λέξεις του 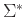 .
Αν
.
Αν
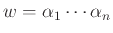 ,
,
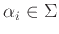 , είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο
, είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο 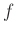 για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
η γλώσσα δηλ. που προκύπτει από τη συγκόλληση των γλωσσών
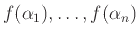 .
.
Αν 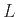 είναι μια γλώσσα ορίζουμε ως συνήθως
είναι μια γλώσσα ορίζουμε ως συνήθως
Θεώρημα 7.4
Αν 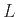 κανονική, και η αντικατάσταση
κανονική, και η αντικατάσταση 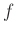 είναι κανονική, τότε η
είναι κανονική, τότε η 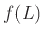 είναι
κανονική γλώσσα.
είναι
κανονική γλώσσα.
Άσκηση 7.32
Αποδείξτε το Θεώρημα 7.4 ακολουθώντας
τη «συνταγή» του σχεδίου απόδειξης που δόθηκε.
Μπορείτε για παράδειγμα να χρησιμοποιήσετε επαγωγή ως προς το μήκος
μιας κανονικής έκφρασης της κανονικής γλώσσας 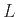 .
.
Ορισμός 7.21
Μια αντικατάσταση 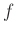 λέγεται ομομορφισμός αν για κάθε
λέγεται ομομορφισμός αν για κάθε
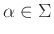 η γλώσσα
η γλώσσα 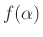 είναι μονοσύνολο.
είναι μονοσύνολο.
Επειδή κάθε πεπερασμένο σύνολο λέξεων είναι κανονική γλώσσα (από τον
ορισμό του τι είναι κανονική γλώσσα) από το προηγούμενο
θεώρημα έπεται ότι οι ομομορφισμοί διατηρούν την κανονικότητα των γλωσσών.
Ορισμός 7.22
Αν 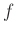 είναι ομομορφισμός και
είναι ομομορφισμός και 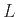 είναι μια γλώσσα, η αντίστροφη ομομορφική
εικόνα της
είναι μια γλώσσα, η αντίστροφη ομομορφική
εικόνα της 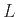 είναι η γλώσσα
είναι η γλώσσα
Θεώρημα 7.5
Αν 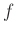 ομομορφισμός και
ομομορφισμός και 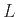 κανονική γλώσσα τότε και η
κανονική γλώσσα τότε και η 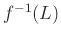 είναι κανονική.
είναι κανονική.
Απόδειξη.
Έστω
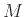
ένα DFA που αναγνωρίζει την
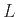
.
Φτιάχνουμε DFA
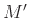
ως εξής: κρατάμε ίδιες καταστάσεις και αρχικές και τελικές
καταστάσεις με το
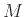
και ορίζουμε μόνο νέα συνάρτηση μετάβασης ως εξής:
αν
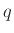
είναι μια κατάσταση του
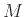
και
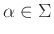
ορίζουμε
Μεταβαίνουμε δηλ. στο
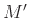
σε εκείνη την κατάσταση όπου θα καταλήγαμε αν στο
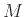
ξεκινάγαμε από την κατάσταση
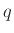
και ακολουθούσαμε τη
λέξη 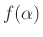
.
Είναι φανερό ότι η λέξη
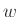
γίνεται αποδεκτή από το
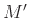
αν και μόνο αν η λέξη
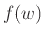
γίνεται αποδεκτή από το
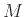
, άρα το DFA αναγνωρίζει τη γλώσσα
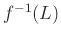
,
οπότε αυτή είναι κανονική.

Άσκηση 7.33
Αν 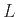 είναι κανονική γλώσσα τότε και η γλώσσα
είναι κανονική γλώσσα τότε και η γλώσσα
είναι κανονική. Με 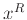 συμβολίζουμε τη λέξη
συμβολίζουμε τη λέξη 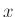 με τα γράμματά της σε
ανάποδη σειρά. Π.χ.
με τα γράμματά της σε
ανάποδη σειρά. Π.χ.
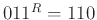 .
.
Υπόδειξη: Δουλέψτε πάνω σε μια κανονική έκφραση για την 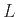 .
.
Mihalis Kolountzakis
2015-11-28
![]() και
και ![]() είναι κανονικές γλώσσες τότε
κανονική είναι και η
είναι κανονικές γλώσσες τότε
κανονική είναι και η
![]() όπως και η γλώσσα
όπως και η γλώσσα ![]() .
Δεν είναι όμως καθόλου προφανές από τον ορισμό των κανονικών εκφράσεων
το αν η συμπληρωματική γλώσσα
.
Δεν είναι όμως καθόλου προφανές από τον ορισμό των κανονικών εκφράσεων
το αν η συμπληρωματική γλώσσα
![]() είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, και
είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, και
![]() μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του
μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του ![]() σε λέξεις του
σε λέξεις του ![]() .
Αν
.
Αν
![]() ,
,
![]() , είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο
, είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο ![]() για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
![]() είναι μια γλώσσα ορίζουμε ως συνήθως
είναι μια γλώσσα ορίζουμε ως συνήθως
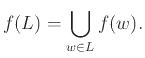
![]() είναι κανονική τότε προκύπτει ως γλώσσα μιας κανονικής έκφρασης
είναι κανονική τότε προκύπτει ως γλώσσα μιας κανονικής έκφρασης ![]() .
Είναι εύκολο να δούμε (αλλά δεν το κάνουμε με λεπτομέρεια εδώ) ότι η γλώσσα
.
Είναι εύκολο να δούμε (αλλά δεν το κάνουμε με λεπτομέρεια εδώ) ότι η γλώσσα
![]() είναι ακριβώς αυτή που προκύπτει αν τροποποιήσουμε την έκφραση
είναι ακριβώς αυτή που προκύπτει αν τροποποιήσουμε την έκφραση ![]() αντικαθιστώντας
κάθε γράμμα
αντικαθιστώντας
κάθε γράμμα ![]() που εμφανίζεται στην
που εμφανίζεται στην ![]() με μια κανονική έκφραση για τη γλώσσα
με μια κανονική έκφραση για τη γλώσσα ![]() .
Άρα η γλώσσα
.
Άρα η γλώσσα ![]() δίδεται από κανονική έκφραση, άρα είναι κανονική.
δίδεται από κανονική έκφραση, άρα είναι κανονική.
![]()
![]() .
.