1.11 Επαναληπτικές Ασκήσεις Κεφαλαίου

Άσκηση 1.36   Δείξτε ότι ο αριθμός 8 διαιρεί το $9^k-1$ για $k \ge 1$.

Άσκηση 1.37   Δείξτε ότι για $n \ge 0$ και $0\le k \le n$ έχουμε

$$\frac{d^k}{dx^k} x^n = \frac{n!}{(n-k)!} x^{n-k}.$$

Άσκηση 1.38   Δείξτε επαγωγικά ότι για $n\ge 1$ ισχύει

$$1^3+2^3+\cdots+n^3 = (1+2+\cdots+n)^2.$$ (1.23)

Άσκηση 1.39   Δείξτε την ισότητα

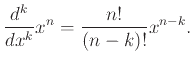
$$\sum_{{\left\{{a_1,\ldots,a_k}\right\}} \subseteq [n]} {1 \over a_1 a_2 \cdots a_k} = n+1,$$

όπου στο άθροισμα υπάρχει ακριβώς ένας προσθετέος για κάθε ένα από τα υποσύνολα ${\left\{{a_1,\ldots,a_k}\right\}}$ του $[n] = {\left\{{1,2,\ldots,n}\right\}}$.

Σημείωση: Ο προσθετέος στο παραπάνω άθροισμα που αντιστοιχεί στο κενό σύνολο ${\left\{{a_1,\ldots,a_k}\right\}}$ του $[n]$ είναι ο 1. Αυτό είναι φυσιολογικό γιατί το γινόμενο μηδενικού πλήθους παραγόντων είναι 1, το ουδέτερο στοιχείο του πολλαπλασιασμού, ακριβώς όπως η τιμή ενός αθροίσματος χωρίς όρους είναι 0, το ουδέτερο στοιχείο της πρόσθεσης.

Σχήμα 1.12: Κύκλοι που ορίζουν χωρία στο επίπεδο

Άσκηση 1.40   Δίνονται $n$ κύκλοι στο επίπεδο. (Δείτε το Σχήμα 1.12.) Αυτοί ορίζουν κάποια χωρία. Δείξτε ότι αυτά μπορούν να χρωματιστούν κόκκινα ή μπλέ με τέτοιο τρόπο ώστε χωρία που έχουν κοινό σύνορο (όχι απλώς κοινή γωνία αλλά ολόκληρο τόξο ως κοινό σύνορο) να έχουν διαφορετικό χρώμα.

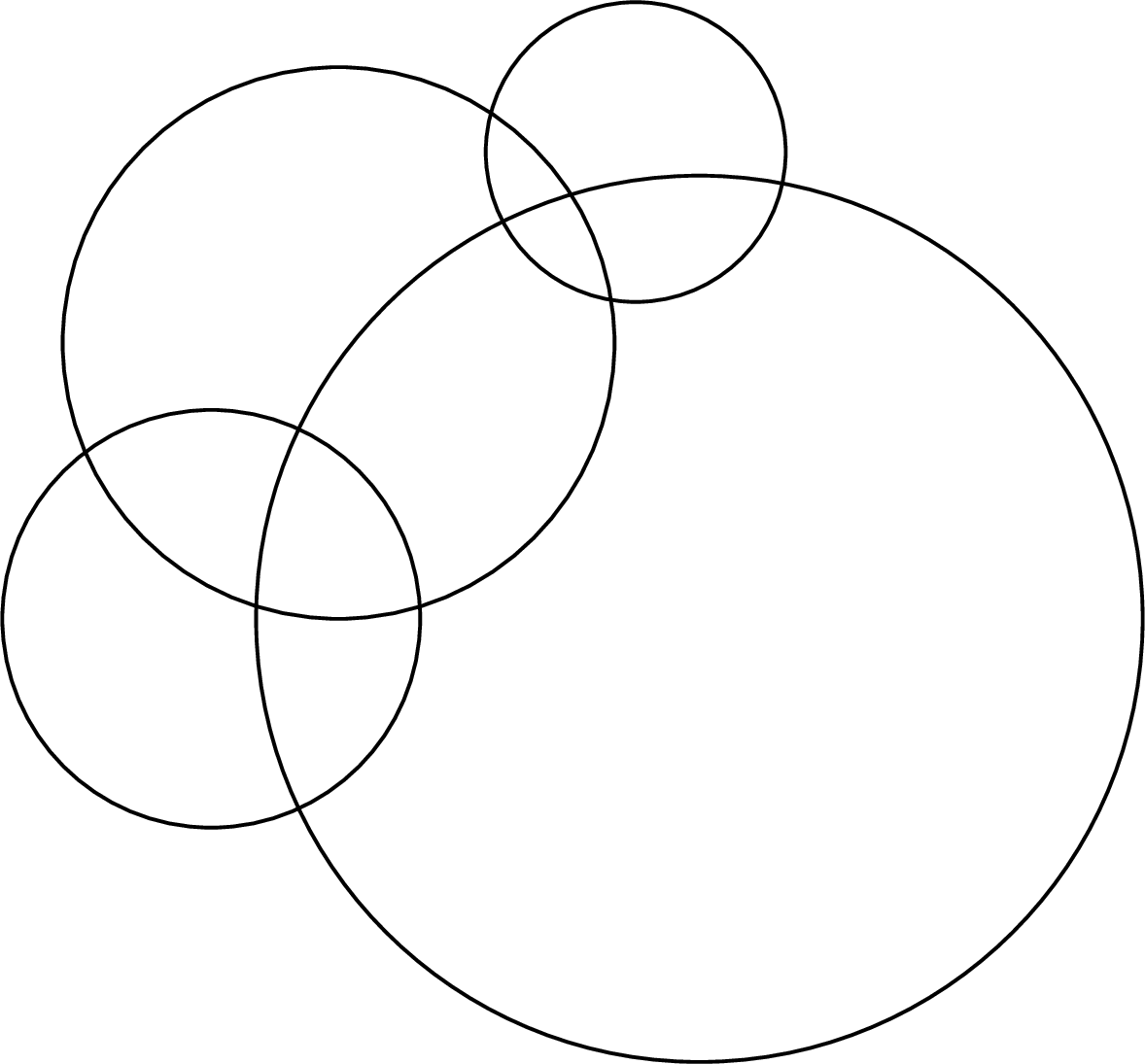
Οι κύκλοι βρίσκονται σε γενική θέση: κάθε δύο από αυτούς είτε τέμνονται είτε είναι ξένοι (δεν μπορούν να εφάπτονται) και δεν υπάρχουν τριπλά σημεία τομής.

Σχήμα 1.13: Η σοκολάτα της Άσκησης 1.41 ($m=4$.$n=5$), και ένα κόψιμο από πάνω προς το κάτω.

Άσκηση 1.41   Έχουμε μια ορθογώνια σοκολάτα που αποτελείται από τετραγωνάκια τοποθετημένα σε $m$ γραμμές και $n$ στήλες. Το τετραγωνάκι όμως της πάνω αριστερά γωνίας (και μόνο αυτό) είναι φτιαγμένο από σαπούνι αντί για σοκολάτα.

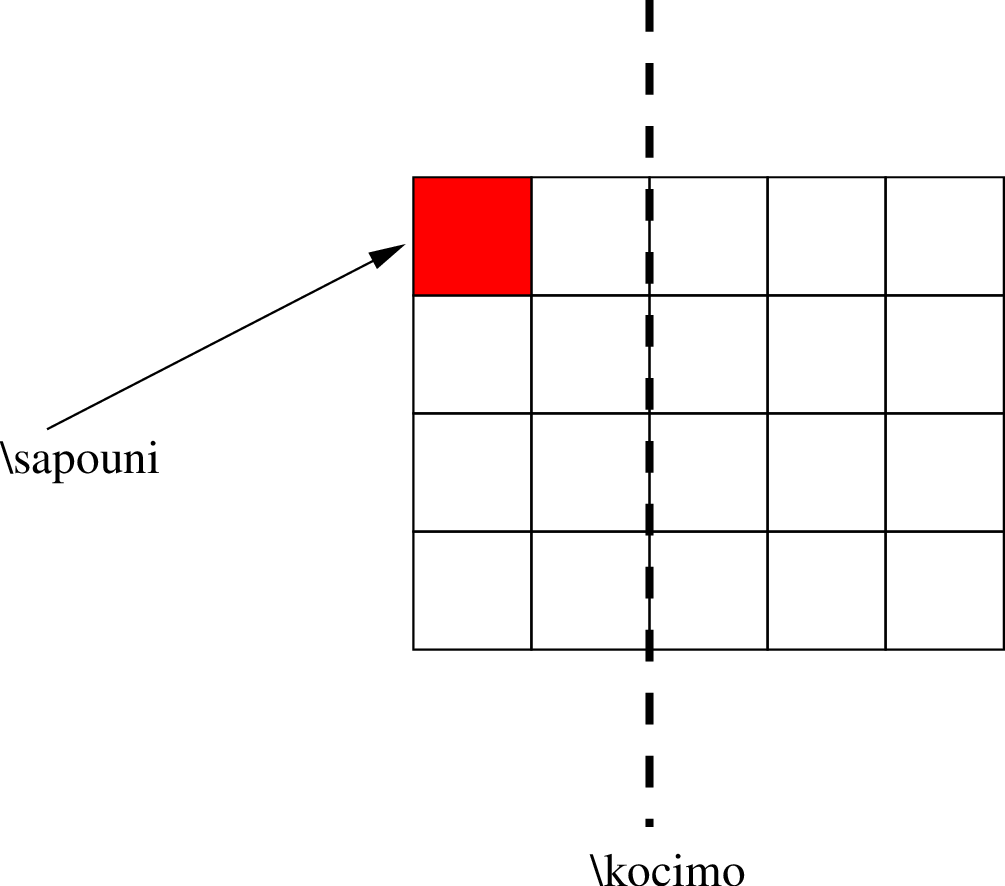
Δύο παίκτες παίζουν το ακόλουθο παιχνίδι. Όταν έρθει η σειρά κάποιου παίκτη αυτός κόβει ένα κομμάτι σοκολάτα και το τρώει. Η $m\times n$ σοκολάτα μπορεί να κοπεί είτε οριζόντια είτε κάθετα αλλά πλήρως, δηλ. αν η σοκολάτα κοπεί οριζόντια τότε αυτή χωρίζεται σε δύο ορθογώνιες σοκολάτες, μια $k\times n$ και μια $(m-k)\times n$, και ο παίκτης διαλέγει και τρώει ένα από τα δύο ορθογώνια κομμάτια. Ομοίως, αν η σοκολάτα κοπεί κάθετα τότε χωρίζεται σε δυο κομμάτια, ένα $m\times k$ και ένα $m\times (n-k)$. (Δείτε Σχήμα 1.13.)

Χάνει ο παίκτης που αναγκάζεται να φάει το τετραγωνάκι με το σαπούνι. Θα θέλατε να παίζατε πρώτος ή δεύτερος; Η απάντηση εξαρτάται από τα $m$ και $n$. Βρείτε (π.χ. μαντέψτε) την απάντηση και αποδείξτε ότι έχετε δίκιο με επαγωγή ως προς το μέγεθος της σοκολάτας ($mn$).

Άσκηση 1.42   Πάνω σε έναν κυκλικό αυτοκινητόδρομο υπάρχουν $n$ σταθμοί ανεφοδιασμού. Η συνολική ποσότητα βενζίνης που έχουν οι $n$ σταθμοί είναι αρκετή ώστε ένα αυτοκίνητο να μπορεί να διαγράψει όλη την διαδρομή (δηλαδή έναν πλήρη κύκλο) με αυτήν. Δε κάνουμε καμία άλλη υπόθεση ούτε για το πόση βενζίνη έχει ο κάθε σταθμός ούτε και για τις μεταξύ τους αποστάσεις. Θεωρούμε οτι το αυτοκίνητο μπορεί να αποθηκεύσει απεριόριστη ποσότητα βενζίνης.

Δείξτε οτι υπάρχει κάποιος από τους $n$ σταθμούς ανεφοδιασμού, τέτοιος ώστε αν το αυτοκίνητο ξεκινήσει από αυτόν θα μπορεί να επιστρέψει σε αυτόν (κινούμενο πάντα προς την ίδια κατεύθυνση).

Άσκηση 1.43   Ένας νεοεκλεγείς πρόεδρος σε μια μεγάλη χώρα με πληθυσμό από λευκούς και έγχρωμους (όλοι οι μη λευκοί) θέλει να ορίσει το υπουργικό του συμβούλιο. Θέλει να χρησιμοποιήσει αυτή του την πράξη ώστε, μεταξύ άλλων, να προωθήσει τη συνεργασία λευκών και έγχρωμων στη χώρα του. Γι' αυτό θεσπίζει τον εξής κανόνα:

κάθε λευκό μέλος του υπουργικού συμβουλίου θα πρέπει να έχει τουλάχιστον τόσους έγχρωμους συνεργάτες όσους και λευκούς και, ομοίως, κάθε έγχρωμο μέλος θα πρέπει να έχει τουλάχιστον τόσους λευκούς συνεργάτες όσους και έγχρωμους.

Οι θέσεις του υπουργικού συμβουλίου είναι δεδομένες όπως και το ποιος συνεργάζεται με ποιον (π.χ. ο υπουργός Οικονομικών συνεργάζεται με όλους, ο υπουργός Άμυνας δε συνεργάζεται με τον υπουργό Γεωργίας, κλπ).

Ο ίδιος ο πρόεδρος είναι κι αυτός μέλος του υπουργικού συμβουλίου και είναι έγχρωμος.

Δείξτε ότι μπορεί πάντα να επιλέξει υπουργούς του κατάλληλου χρώματος ώστε να πετύχει το σκοπό του αυτό.

Υπόδειξη: Πάρτε ένα υπουργικό συμβούλιο που να μεγιστοποιεί τις συνεργασίες μεταξύ λευκών και μαύρων. Τι παρατηρείτε;

Άσκηση 1.44   Ας είναι $A_j \subseteq X, j=1,2,\ldots,N,$ κάποια σύνολα μεγέθους $k$ το καθένα, διαφορετικά μεταξύ τους και τέτοια ώστε η τομή οποιωνδήποτε $k+1$ από τα σύνολα $A_j$ είναι μη κενή.

Τότε και η τομή όλων των $A_j$ είναι μη κενή.

Υπόδειξη: Υποθέστε ότι η τομή είναι κενή και καταλήξτε σε άτοπο. Αν είναι $A_1 = {\left\{{x_1, x_2, \ldots, x_k}\right\}}$ τότε θα υπάρχει κάποιο σύνολο από τα $A_2, \ldots, A_N$ που δεν περιέχει το $x_1$, κάποιο που δεν περιέχει το $x_2$, κλπ.

Σχήμα 1.14: Για την Άσκηση 1.45

Άσκηση 1.45   Ας είναι ${\mathcal{F}}$ μια πεπερασμένη οικογένεια από υποσύνολα ενός συνόλου $X$. Αν είναι $E \subseteq X$ ένα πεπερασμένο σύνολο μεγέθους $k$, λέμε ότι η οικογένεια ${\mathcal{F}}$ διασπά το σύνολο $E$ αν ο αριθμός των διαφορετικών συνόλων

$$F\cap E$$

(όπου $F \in {\mathcal{F}}$), ισούται με $2^k$. Όλα δηλ. τα υποσύνολα του $E$ «φτιάχνονται» από τα σύνολα της ${\mathcal{F}}$ περιορισμένα στο $E$.

Δείξτε ότι κάθε οικογένεια ${\mathcal{F}}$ μεγέθους $N=\vert{\mathcal{F}}\vert$ διασπά τουλάχιστον $N$ διαφορετικά υποσύνολα του $X$.

Άσκηση 1.46   Ποιες από τις παρακάτω γενικευμένες προτάσεις είναι μεταξύ τους ισοδύναμες;

1. $(p \wedge q) \vee ({\sim p} \wedge {\sim} q)$
2. ${\sim} p \vee q$
3. $(p \vee {\sim} q) \wedge (q \vee {\sim} p)$
4. ${\sim}(p \vee q)$
5. $(q \wedge p) \vee {\sim} p$
6. $p \Leftrightarrow q$
7. $p\Rightarrow q$
8. $q \Rightarrow p$
9. $p \vee {\sim p}$
10. $q \vee {\sim q}$

Άσκηση 1.47   Από μια συνηθισμένη 88 σκακιέρα έχουμε αφαιρέσει την πάνω αριστερά και την κάτω δεξιά γωνία (απομένουν δηλ. 62 τετράγωνα). Μπορείτε να καλύψετε αυτή τη σκακιέρα με ντόμινα (ζεύγη δηλ. από τετράγωνα που έχουν μια κοινή πλευρά) που όμως δεν επιτρέπεται να αλληλοεπικαλύπτονται;