Αστροφυσική ϒψηλών Ενεργειών
Απόστολος Μαστιχιάδης
Καθηγητής Τμήματος Φυσικής Πανεπιστημίου Αθηνών
Νεκτάριος Βλαχάκης
Επίκουρος Καθηγητής Τμήματος Φυσικής Πανεπιστημίου
Αθηνών



Αστροφυσική ϒψηλών Ενεργειών
Απόστολος Μαστιχιάδης
Καθηγητής Τμήματος Φυσικής Πανεπιστημίου Αθηνών
Νεκτάριος Βλαχάκης
Επίκουρος Καθηγητής Τμήματος Φυσικής Πανεπιστημίου
Αθηνών




Αστροφυσική ϒψηλών Ενεργειών
Συγγραφή:
Απόστολος Μαστιχιάδης
Νεκτάριος Βλαχάκης
Κριτικός αναγνώστης:
Νικόλαος Κυλάφης
Συντελεστές έκδοσης:
ΓΛΩΣΣΙΚΗ ΕΠΙΜΕΛΕΙΑ: Δημήτριος Καλλιάρας
![]() Copyright ΣΕΑΒ, 2015
Copyright ΣΕΑΒ, 2015
Το παρόν έργο αδειοδοτείται υπό τους όρους της άδειας Creative Commons
Αναφορά Δημιουργού – Μη Εμπορική Χρήση – ΄Οχι Παράγωγα Εργα 3.0.
Για να δείτε ένα αντίγραφο της άδειας αυτής επισκεφτείτε τον ιστότοπο
https://creativecommons.org/licenses/by-_nc-_nd/3.0/gr/
Σύνδεσμος Ελληνικών Ακαδημαϊκών Βιβλιοθηκών
Εθνικό Μετσόβιο Πολυτεχνείο
Ηρώων Πολυτεχνείου 9, 15780 Ζωγράφου
ISBN: 978-960-603-142-7
Ενώ τα κλασικά όργανα αστρονομικής παρατήρησης, δηλαδή το ανθρώπινο μάτι στην αρχή και τα οπτικά τηλεσκόπια αργότερα, έδιναν μία εικόνα του Σύμπαντος που βρίσκεται σε θερμοδυναμική ισορροπία, οι πρόσφατες παρατηρήσεις σε όλο το εύρος του ηλεκτρομαγνητικού φάσματος φανερώνουν ένα Σύμπαν γεμάτο από ενεργητικά φαινόμενα: καταρρεύσεις αστέρων, εκρήξεις υπερκαινοφανών, δημιουργία δίσκων προσαύξησης, εκροές σχετικιστικού πλάσματος, εκλάμψεις ακτίνων γ, επιτάχυνση σωματιδίων και παραγωγή ακτινοβολίας Χ και γ. Τα φαινόμενα αυτά συνδέονται κυρίως με συμπαγή αστροφυσικά αντικείμενα, δηλαδή αστέρες νετρονίων και μελανές οπές στις διάφορες εκφάνσεις τους: pulsars, διπλά συστήματα ακτίνων Χ, quasars και άλλους πυρήνες ενεργών γαλαξιών. Αν και τα παραπάνω διαφέρουν πολύ μεταξύ τους, ωστόσο σχετίζονται με διάφορους κοινούς μηχανισμούς υψηλών ενεργειών και συνιστούν μία νέα (και πολύ λιγότερο οικεία) εικόνα του Σύμπαντος από αυτή που γνώριζαν οι άνθρωποι μέχρι τα μέσα του εικοστού αιώνα. Αυτή η ανάγκη εξερεύνησης της σχετικιστικής πλευράς του Σύμπαντος δημιούργησε την Αστροφυσική ϒψηλών Ενεργειών.
Σκοπός της Αστροφυσικής ϒψηλών Ενεργειών λοιπόν είναι να μελετήσει τα αστροφυσικά αντικείμενα που συνδέονται με τα φαινόμενα υψηλών ενεργειών και να κατανοήσει εκείνους των φυσικούς μηχανισμούς που είναι υπεύθυνοι για τη δημιουργία αυτών των φαινομένων. Οι δυσκολίες ενός τέτοιου εγχειρήματος είναι προφανείς. Οι φυσικοί μηχανισμοί που παρουσιάζουν ενδιαφέρον είναι αδύνατον να αναπαραχθούν στο εργαστήριο – πώς θα μπορούσαμε άραγε να πλησιάσουμε σε κάποιο εργαστήριο τις συνθήκες που επικρατούν στην άμεση γειτονιά μιας μελανής οπής ή στο ωστικό κύμα που δημιουργείται κατά την έκρηξη ενός υπερκαινοφανούς; Το ζητούμενο συνεπώς είναι η κατάλληλη επιλογή φυσικών νόμων και η κατασκευή μοντέλων που να προσομοιάζουν τις φυσικές συνθήκες στις πηγές και ταυτόχρονα να μπορούν να εξηγήσουν με κάποια πειστικότητα τις διάφορες παρατηρήσεις. Είναι εντυπωσιακό να αναλογισθεί κανείς, πόσα προβλήματα της Αστροφυσικής ϒψηλών Ενεργειών, όσο ακραία κι αν αυτά φάνηκαν αρχικά, ερμηνεύθηκαν τελικά με βάση γνωστές φυσικές διαδικασίες, χωρίς να χρειασθεί να καταφύγουμε σε διάφορου τύπου εξωτικές λύσεις. (Για παράδειγμα, όταν ανακαλύφθηκαν οι quasars, πολλοί μίλησαν για ανάγκη εισαγωγής «νέας Φυσικής» προκειμένου να εξηγηθούν οι πραγματικά περίεργες ιδιότητές τους. Τελικά η πρόσπτωση ύλης σε μελανές οπές, φαινόμενο που παρατηρείται, σε πολύ μικρότερες κλίμακες, ακόμα και στον Γαλαξία μας, έδωσε μία ικανοποιητική απάντηση στο πρόβλημα της τεράστιας έκλυσης ενέργειας που παρατηρείται).
Μία άλλη σημαντική διάσταση του προβλήματος είναι η συγγένεια μερικών τουλάχιστον θεμάτων που απασχολούν την Αστροφυσική ϒψηλών Ενεργειών και τη Φυσική της Κοσμικής Ακτινοβολίας. Για παράδειγμα, οι παρατηρήσεις σε ακτίνες γ φανερώνουν την ύπαρξη σχετικιστικών σωματιδίων σε αστροφυσικές πηγές όπως τα κελύφη υπερκαινοφανών, οι pulsars και οι ενεργοί γαλαξίες. Θα μπορούσε λοιπόν τα σωματίδια της κοσμικής ακτινοβολίας τα οποία παρατηρούμε να παράγονται σε κάποιες από αυτές τις πηγές και στη συνέχεια να διαχέονται στον Γαλαξία μας φτάνοντας τελικά στη Γη; Η συνάφεια των παραπάνω τομέων δεν σταματάει όμως εδώ. Από παρατηρήσεις του δίσκου του Γαλαξία μας στα ραδιοκύματα και στις ακτίνες γ παίρνουμε πληροφορίες για την κοσμική ακτινοβολία στις περιοχές αυτές. Και βέβαια επειδή η κοσμική ακτινοβολία είναι φορτισμένα σωματίδια υψηλών ενεργειών, οι φυσικές αρχές οι οποίες διέπουν τη διάδοση και ακτινοβολία τους στο Ηλιακό μας Σύστημα είναι οι ίδιες με τις φυσικές αρχές που διέπουν τη διάδοση και ακτινοβολία των αντίστοιχων σωματιδίων στις αστροφυσικές πηγές. Ακόμα και οι αδρονικοί και ηλεκτρομαγνητικοί καταιονισμοί οι οποίοι δημιουργούνται κατά την είσοδο των σωματιδίων της κοσμικής ακτινοβολίας στη γήινη ατμόσφαιρα μπορεί να είναι ίδιοι με αυτούς που δημιουργούνται (τηρουμένων κάποιων αναλογιών) σε διάφορα αστροφυσικά περιβάλλοντα. Δεν είναι τυχαίο άλλωστε ότι σήμερα ένα μεγάλο μέρος της Φυσικής της Κοσμικής Ακτινοβολίας, της Αστροφυσικής ϒψηλών Ενεργειών και διαφόρων παρατηρησιακών τομέων όπως της Αστρονομίας Ακτίνων γ και της Αστρονομίας Νετρίνων ενώνονται κάτω από το κοινό όνομα Αστροσωματιδιακή Φυσική.
Η Αστροφυσική ϒψηλών Ενεργειών, όπως και πολλοί άλλοι κλάδοι άλλωστε, ωφελήθηκε από μια σειρά από επιστημονικά και τεχνολογικά επιτεύγματα. Αυτά είναι:
Ερευνητικά η Αστροφυσική ϒψηλών Ενεργειών αντιμετωπίζει σήμερα ένα πλήθος ερωτημάτων που ζητούν πιεστικά απάντηση. Γενικά αυτά σχετίζονται με τη φύση των Κοσμικών Επιταχυντών και τους Μηχανισμούς Ακτινοβολίας. Εξειδικεύοντας θα λέγαμε ότι μερικά από τα προβλήματα αυτά είναι:
Το πρόβλημα της επιτάχυνσης σωματιδίων που εμφανίζεται σε ένα πλήθος περιπτώσεων είναι τόσο καίριο ώστε να το περιλάβει το Ινστιτούτο Φυσικής των Ηνωμένων Πολιτειών ως ένα από πιο σημαντικά της τρέχουσας δεκαετίας, όχι μόνο στον χώρο της Αστροφυσικής, αλλά της Φυσικής γενικότερα.
Παρόλο που η Αστροφυσική ϒψηλών Ενεργειών καλύπτει ένα μεγάλο αριθμό θεμάτων και εκτείνεται προς διάφορες περιοχές της σύγχρονης Αστροφυσικής, οι ανάγκες του παρόντος μαθήματος μας υποχρεώνουν να περιορίσουμε τη θεματολογία και να εστιασθούμε κυρίως στην παρουσίαση των βασικών αρχών του κλάδου, δηλαδή στην παρουσίαση εκείνων των φυσικών διαδικασιών που χρησιμοποιούνται ως εργαλεία στην κατανόηση των διαφόρων αστροφυσικών φαινομένων υψηλών ενεργειών. ΄Ετσι το μέρος της Αστροφυσικής ϒψηλών Ενεργειών με το οποίο θα ασχοληθούμε εδώ προσπαθεί να απαντήσει στα εξής ερωτήματα: Ποιες, από τις πολλές, φυσικές διαδικασίες ακτινοβολίας που υπάρχουν έχουν σχέση με την παρατηρούμενη ακτινοβολία από πηγές υψηλών ενεργειών και τι μας φανερώνουν για τη φύση των πηγών αυτών; Ποιος μηχανισμός είναι υπεύθυνος για την επιτάχυνση των σωματιδίων της κοσμικής ακτινοβολίας και ποιος για το ενεργειακό φάσμα σωματιδίων που, μέσω συγκεκριμένων διαδικασιών ακτινοβολίας παράγουν μη-θερμικά φάσματα φωτονίων; ΄Οπως θα δούμε οι απαντήσεις ποικίλλουν κατά περίπτωση όπως επίσης και ο βαθμός αποδοχής τους. Επίσης θα περιγράψουμε τους πίδακες πλάσματος με σχετικιστική μακροσκοπική κίνηση οι οποίοι σχετίζονται με πληθώρα διαδικασιών υψηλών ενεργειών, καθώς και τους δίσκους προσαύξησης μέσω των οποίων μετατρέπεται βαρυτική δυναμική ενέργεια σε άλλη μορφή, η οποία τελικά μπορεί επίσης να συνδέεται με διαδικασίες υψηλών ενεργειών. Ελπίζουμε ότι η γενική παρουσίαση των φυσικών διαδικασιών και μετά η εφαρμογή σε συγκεκριμένα αστροφυσικά φαινόμενα υψηλών ενεργειών θα βοηθήσει σε μία καλύτερη κατανόηση του αντικειμένου ενός τόσο ενδιαφέροντος όσο και σύγχρονου κλάδου.
Η Αστροφυσική ϒψηλών Ενεργειών (από εδώ και πέρα θα αναφερόμαστε σε αυτή με το ακρωνύμιο ΑϒΕ) δημιουργήθηκε ως ένας ακόμα κλάδος της Αστροφυσικής μετά από ορισμένες παρατηρήσεις που έδειξαν ότι στον Γαλαξία μας, αλλά και πέρα από αυτόν, υπάρχουν πηγές και φαινόμενα που φανερώνουν την ύπαρξη σωματίων και φωτονίων υψηλών ενεργειών. Στο πρώτο μέρος του παρόντος κεφαλαίου θα αναφερθούμε στις παρατηρήσεις της ΑϒΕ και θα επιχειρήσουμε μία ταξινόμηση των πηγών με βάση τη συχνότητα στην οποία αυτές ανιχνεύθηκαν. Στο δεύτερο μέρος θα αναπτύξουμε τα κυριότερα χαρακτηριστικά της Κοσμικής Ακτινοβολίας, των φορτισμένων σωματιδίων υψηλών ενεργειών που ανιχνεύονται στη Γη και τα οποία, σύμφωνα με όλες τις ενδείξεις, πρέπει να συνδέονται με τις πηγές της ΑϒΕ.
΄Οπως είναι γνωστό, ο μόνος τρόπος εξαγωγής πληροφοριών για τη φύση αστροφυσικών πηγών είναι η μελέτη του Ηλεκτρομαγνητικού φάσματος που αυτές εκπέμπουν. Τα προς μελέτη συνεχή φάσματα μπορούμε να τα διαφοροποιήσουμε σε θερμικά και μη θερμικά.
Θερμικά είναι τα φάσματα εκείνα τα οποία προέρχονται είτε από εκπομπή ακτινοβολίας που βρίσκεται σε θερμοδυναμική ισορροπία με την ύλη είτε από εκπομπή ακτινοβολίας από πλάσμα το οποίο έχει μεν θερμική κατανομή αλλά δεν βρίσκεται σε θερμοδυναμική ισορροπία με την εκπεμπόμενη ακτινοβολία. Η πρώτη περίπτωση είναι η γνωστή εκπομπή μελανού σώματος το φάσμα του οποίου περιγράφεται από τον νόμο του Planck. Για παράδειγμα, η εκπομπή από την επιφάνεια των αστέρων μπορεί να αποδοθεί με ικανοποιητικό τρόπο στην εκπομπή μελανού σώματος μίας συγκεκριμένης θερμοκρασίας. Η δεύτερη περίπτωση είναι λιγότερο γνωστή και πρόκειται για τη θερμική ακτινοβολία πέδης (bremsstrahlung), για την ακτινοβολία δηλαδή αραιού θερμού πλάσματος. Η εκπομπή ακτίνων Χ από ωστικά κύματα υπερκαινοφανών όπως κι αυτή από σμήνη γαλαξιών αποδίδεται σε αυτόν τον μηχανισμό.
Μία βασική έννοια που καθορίζει και τη μορφή του εκπεμπόμενου φάσματος είναι αυτή των συγκρούσεων είτε μεταξύ σωματιδίων είτε μεταξύ σωματιδίων-φωτονίων. ΄Οταν ο ρυθμός των συγκρούσεων είναι μεγάλος και ο χρόνος εξέλιξης του συστήματος μακρύς, τότε εν γένει το σύστημα έρχεται σε κάποια θερμική ισορροπία καθώς τα σωμάτια που έχουν μεγαλύτερη ενέργεια τη μοιράζονται αποτελεσματικά, μέσω των συγκρούσεων, με αυτά που έχουν μικρότερη.
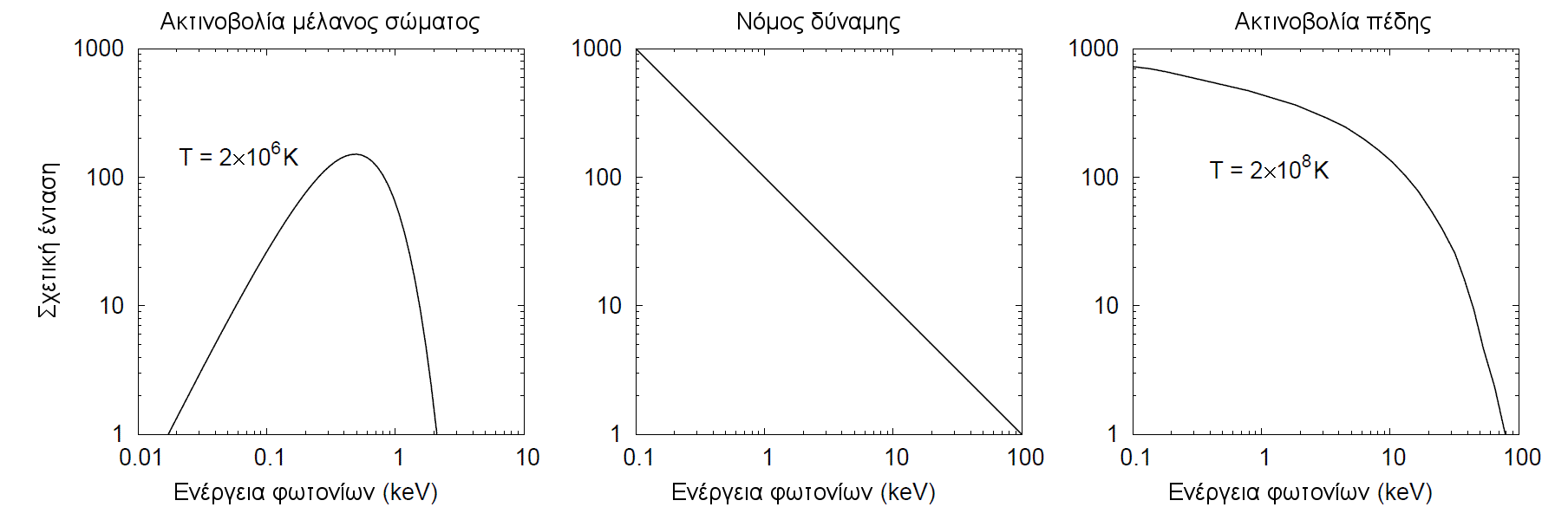
Σε πολλές περιπτώσεις όμως το αστροφυσικό πλάσμα είναι αραιό και οι συγκρούσεις μεταξύ των σωματιδίων που το απαρτίζουν εξαιρετικά σπάνιες1 . Σε αυτές τις περιπτώσεις το φάσμα φωτονίων που εκπέμπεται χαρακτηρίζεται ως μη θερμικό και συνήθως έχει τη μορφή νόμου δύναμης, δηλαδή
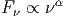 | (2.1) |
όπου ν η συχνότητα και α ο φασματικός δείκτης. Το σχήμα 2.1 δείχνει τη φασματική αυτή συνάρτηση και, για σύγκριση, τις δύο θερμικές φασματικές συναρτήσεις, δηλαδή το φάσμα μελανού σώματος και αυτό της θερμικής ακτινοβολίας πέδης.
Η πρώτη από τις νέες αστρονομίες που αναπτύχθηκαν ήταν η ραδιοαστρονομία. Αυτό βέβαια συνέβη γιατί, πριν ξεκινήσει η λεγόμενη διαστημική εποχή στα τέλη της δεκαετίας του 1950, παρατηρήσεις μπορούσαν να γίνουν μόνον από την επιφάνεια της Γης και καθώς τα ραδιοκύματα δεν απορροφώνται από την ατμόσφαιρα, η περιοχή αυτή ενδεικνυόταν. Παρόλο που ο τομέας ουσιαστικά εμφανίστηκε το 1930 με τις παρατηρήσεις του Carl Jansky, οι πρώτες οργανωμένες προσπάθειες δεν ξεκίνησαν παρά μετά τον Β΄ Παγκόσμιο Πόλεμο με τις εξελίξεις στα ηλεκτρονικά και στους υπολογιστές. Ραδιοεκπομπή ανακαλύφθηκε από μία πλειάδα αντικειμένων. Σε μερικές περιπτώσεις αυτή η εκπομπή μπορούσε να συνδεθεί αμέσως με φαινόμενα γνωστά από τα οπτικά μήκη κύματος, π.χ. εκπομπή από τον ΄Ηλιο ή εκπομπή από θερμά ηλεκτρόνια σε περιοχές ιονισμένου υδρογόνου. Σε πολλές άλλες περιπτώσεις ωστόσο η σύνδεση αυτή δεν ήταν άμεση και δημιούργησε εύλογα ερωτήματα για το είδος των πηγών και των φυσικών διαδικασιών που συνδέονται με αυτές. ΄Ενα ακόμα ενδιαφέρον παρατηρησιακό δεδομένο, κοινό των νέων πηγών, ήταν ότι η ραδιοεκπομπή δεν είχε θερμική προέλευση αλλά μπορούσε να περιγραφεί με νόμο δύναμης. Γρήγορα έγινε αντιληπτό ότι η παρατηρούμενη εκπομπή ήταν ακτινοβολία σύγχροτρον, η ακτινοβολία δηλαδή που εκπέμπουν σχετικιστικά ηλεκτρόνια ευρισκόμενα μέσα σε μαγνητικό πεδίο. Συνεπώς οι παρατηρήσεις στα ραδιοκύματα μας έδωσαν τις πρώτες ενδείξεις για την ύπαρξη σχετικιστικού πλάσματος σε κοσμικές πηγές και παίζουν έναν σημαντικό ρόλο στην εξέλιξη της ΑϒΕ.
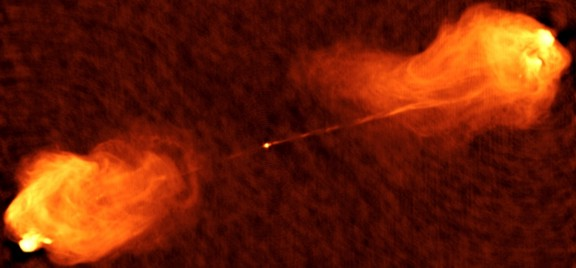

Η σημαντικότερη ανακάλυψη της ραδιοαστρονομίας, τουλάχιστον όσον αφορά το αντικείμενό μας, είναι αναμφισβήτητα οι ραδιογαλαξίες και οι quasars, αντικείμενα που ανήκουν στους Ενεργούς Γαλαξίες. Αυτοί παρουσιάζουν έντονη εκπομπή στα ραδιοκύματα και η μορφολογία τους είναι πολύπλοκη διότι εκτός από την κεντρική περιοχή (τον πυρήνα τους) παρουσιάζουν συχνά συμμετρικά τεράστιους λοβούς γεμάτους σχετικιστικό πλάσμα που, σε ορισμένες περιπτώσεις, βρίσκονται εκατοντάδες kiloparsecs από τον κεντρικό γαλαξία. Οι ραδιολοβοί τροφοδοτούνται με ενέργεια από τον πυρήνα μέσω πιδάκων, επιμηκών δομών που μπορούν να διατηρούν την κατευθυντικότητά τους ακόμα και σε κλίμακες 1 : 106. Ειδικά οι quasars έχουν τόσο ισχυρή εκπομπή ώστε να μπορούμε να τους ανιχνεύουμε σε κοσμολογικές αποστάσεις, από εποχές δηλαδή που το Σύμπαν ήταν αρκετά νεότερο από ότι είναι σήμερα. Οι σχετικές παρατηρήσεις δείχνουν ότι η λαμπρότητα που ακτινοβολείται από τους πυρήνες τους είναι μη θερμική και κατά πολλές χιλιάδες φορές μεγαλύτερη από τη συνολική λαμπρότητα του Γαλαξία μας.
Οι ανακαλύψεις όμως της ραδιοαστρονομίας που αφορούν την ΑϒΕ δεν σταματούν εδώ: Το 1967 οι Bell και Hewish ανακαλύπτουν τους pulsars, την πρώτη απόδειξη για την ύπαρξη των αστέρων νετρονίων, οι οποίοι είναι συμπαγή αστρικά υπολείμματα με ακτίνες ~10 km και κεντρικές πυκνότητες οι οποίες υπερβαίνουν την πυρηνική. Επιπλέον οι pulsars είναι ισχυρά μαγνητισμένοι και ταχύτατα περιστρεφόμενοι. Η παρατηρούμενη ραδιοεκπομπή τους προφανώς οφείλεται σε ηλεκτρόνια υψηλών ενεργειών τα οποία επιταχύνονται στις μαγνητόσφαιρές τους. Σήμερα είναι γνωστοί πάνω από 1000 pulsars με μέση περίοδο περί το 1 sec ενώ ο αριθμός τους στον Γαλαξία μας υπολογίζεται πολύ μεγαλύτερος.
Τέλος μία ακόμα ανακάλυψη της ραδιοαστρονομίας αφορά την εκπομπή ακτινοβολίας σύγχροτρον από κελύφη υπερκαινοφανών. Αυτό αποτελεί αδιαμφισβήτητη απόδειξη ότι τα ωστικά κύματα που δημιουργούνται κατά την έκρηξη των υπερκαινοφανών επιταχύνουν σωματίδια σε υψηλή ενέργεια. Αυτή υπερβαίνει κατά πολλές τάξεις μεγέθους την κινητική ενέργεια που θα είχαν τα σωματίδια εάν απλώς είχαν την ταχύτητα του κύματος.
Η αστρονομία ακτίνων Χ ξεκίνησε αργότερα από τη ραδιοαστρονομία. Ο λόγος είναι ότι οι ακτίνες Χ εξωγήινης προέλευσης δεν φτάνουν στην επιφάνεια της Γης λόγω της φωτοηλεκτρικής απορρόφησης που αυτές υφίστανται από τα άτομα και τα μόρια της γήινης ατμόσφαιρας. Συνεπώς οι αστρονόμοι χρειάστηκε να περιμένουν τη δημιουργία ρουκέτων που να είναι ικανές να σηκώσουν ανιχνευτές πάνω από την ατμόσφαιρα και αυτό επιτεύχθηκε στις αρχές της δεκαετίας του 1960. Παρόλο που οι πρώτες αυτές παρατηρήσεις διαρκούσαν μόνο περί τα πέντε λεπτά ήταν αρκετές να δείξουν ότι ο ουρανός είναι γεμάτος από πηγές ακτίνων Χ.
Η πρώτη αποστολή που έφερε την αστρονομία ακτίνων Χ στο προσκήνιο ήταν αυτή του δορυφόρου UHURU, στη δεκαετία του 1970, ο οποίος και χαρτογράφησε τον ουρανό σε αυτές τις συχνότητες. Την αποστολή του UHURU ακολούθησαν πολλές άλλες αποστολές, με μεγαλύτερη διακριτική ικανότητα κι ευαισθησία, που έμειναν σε τροχιά από μήνες μέχρι και χρόνια γύρω από τη Γη και μας έδωσαν μία λεπτομερή εικόνα του ουρανού στις ακτίνες Χ.
Ως προς την ΑϒΕ στον Γαλαξία μας παρατηρήθηκαν πηγές που εκπέμπουν παλμούς σταθερής περιόδου και διαπιστώθηκε ότι αυτές προέρχονται από αστέρες νετρονίων που ταυτόχρονα είναι μέλη διπλών αστρικών συστημάτων. Η εξήγηση που δόθηκε και που σήμερα είναι καθολικά αποδεκτή είναι ότι υλικό εκρέει από τον αστέρα συνοδό και προσπίπτει στον αστέρα νετρονίων. Κατά την πρόσπτωση η βαρυτική δυναμική ενέργεια του υλικού μετατρέπεται σε κινητική και κατόπιν σε θερμότητα με αποτέλεσμα αυτό να φτάνει σε θερμοκρασία πολλών εκατομμυρίων βαθμών όταν πλησιάζει την επιφάνεια του αστέρα νετρονίων και φυσικά να ακτινοβολεί στις ακτίνες Χ. Στην περίπτωση των παλλόμενων πηγών ακτίνων Χ οι μάζες των αστέρων οι οποίες υπολογίζονται με δυναμικές μεθόδους είναι σύμφωνες με αυτές που περιμένουμε θεωρητικά για αστέρες νετρονίων. ϒπάρχουν ωστόσο μερικές άλλες πηγές ακτίνων Χ σε διπλά συστήματα οι οποίες δεν παρουσιάζουν καμία περιοδικότητα στην εκπομπή τους και των οποίων οι μάζες είναι κατά πολύ μεγαλύτερες των αστέρων νετρονίων. Σε αυτήν την περίπτωση οι πηγές ακτίνων Χ ίσως είναι μελανές οπές.
΄Αλλες εξωγαλαξιακές πηγές ακτίνων Χ είναι οι ενεργοί γαλαξίες. Η έντονη εκπομπή (που πολλές φορές φτάνει σε μεγάλα πολλαπλάσια της ισχύος του Γαλαξία μας σε όλες τις συχνότητες) συνοδεύεται από ταχύτατες αυξομειώσεις της έντασης που υποδεικνύει ότι όλη αυτή η ακτινοβολία παράγεται σε μια περιοχή που δεν ξεπερνάει σε διαστάσεις το Ηλιακό μας Σύστημα. Εικάζεται ότι οι ακτίνες Χ παράγονται από τη θέρμανση της ύλης καθώς αυτή προσπίπτει σε μια μελανή οπή με μάζα που είναι κατά πολλά εκατομμύρια φορές μεγαλύτερη της μάζας του Ηλίου. Σύμφωνα με αυτήν τη θεώρηση οι Ενεργοί Γαλαξίες είναι μία μεγεθυμένη έκδοση των πηγών ακτίνων Χ που περιέχουν μελανές οπές του Γαλαξία μας.
Οι ακτίνες γ αποτελούν μία μεγάλη περιοχή του Η/Μ φάσματος. Πράγματι, με τις παρατηρήσεις να ξεκινούν από 100 keV (περιοχή μαλακών ακτίνων γ) και να φτάνουν έως 30 TeV (περιοχή ακτίνων γ πολύ υψηλών ενεργειών), αυτές καλύπτουν περίπου 9 τάξεις μεγέθους. Είναι φυσικό λοιπόν η αστρονομία ακτίνων γ να υποδιαιρείται περαιτέρω σε περιοχές ανάλογα με την ενέργεια παρατήρησης. ΄Ετσι μπορούμε πλέον να μιλάμε για αστρονομία ακτίνων γ σε
Καθεμία από τις παραπάνω περιοχές έχει διαφορετικές τεχνικές παρατήρησης, παρουσιάζει διαφορετικές ευαισθησίες και έχει να επιδείξει διαφορετικές πηγές. Επίσης διάφοροι φυσικοί μηχανισμοί είναι υπεύθυνοι για την παραγωγή ακτίνων γ. Θα μπορούσαμε να πούμε ότι για τις χαμηλές ενέργειες αυτοί είναι κυρίως θερμικής φύσεως, ενώ για τις υψηλές ενέργειες είναι μη θερμικής. Οι παρατηρήσεις από 30 keV μέχρι 30 GeV γίνονται από το Διάστημα λόγω της αδιαφάνειας της γήινης ατμόσφαιρας σε αυτές τις ενέργειες. Από 500 GeV έως 30 TeV γίνονται από την επιφάνεια της Γης με ανιχνευτές ακτινοβολίας Cherenkov οι οποίοι ανιχνεύουν την εν λόγω ακτινοβολία που παράγεται κατά την είσοδο πολύ ενεργητικών ακτίνων γ στην ατμόσφαιρα.
Η μεγάλη ώθηση στην αστρονομία ακτίνων γ δόθηκε με την εκτόξευση του αμερικάνικου δορυφόρου Compton Gamma Ray Observatory (CGRO) το 1991 και συνεχίστηκε με το τηλεσκόπιο Fermi (2008 – σήμερα) το οποίο έχει ανιχνεύσει πολλές εκατοντάδες πηγές όπως pulsars, κελύφη υπερκαινοφανών, ενεργούς γαλαξίες και εκλάμψεις ακτινοβολίας γάμμα (Gamma-Ray Bursts).
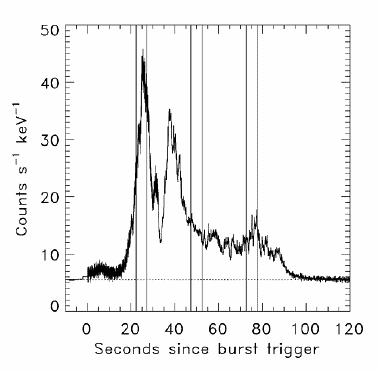
Ειδική μνεία πρέπει να γίνει στις τελευταίες, διότι είναι ένα φαινόμενο που αφορά κυρίως αυτήν την ακτινοβολία. Οι εκλάμψεις ακτινοβολίας γάμμα ανακαλύφθηκαν εντελώς τυχαία τη δεκαετία του 1960 και από τότε παραμένουν ένα από τα πιο αινιγματικά φαινόμενα όχι μόνο της ΑϒΕ αλλά ολόκληρης της Αστροφυσικής. ΄Οπως φανερώνει και η ονομασία τους πρόκειται για εκλάμψεις στις ακτίνες γ ενέργειας ~500 keV που εμφανίζονται αιφνίδια σε κάποιο σημείο του ουρανού, διαρκούν, ανάλογα με την περίπτωση, από κλάσματα του δευτερολέπτου έως και μερικά δευτερόλεπτα και μετά σβήνουν κι εξαφανίζονται.

Η μικρή διάρκειά τους έκανε πολύ δύσκολο τον εντοπισμό τους και παρόλο που ολόκληρα πειράματα αφιερώθηκαν στην κατανόησή τους, για τριάντα περίπου χρόνια ήταν αδύνατος ο προσδιορισμός κάποιας πηγής που να συνδέεται με το φαινόμενο. Τη δεκαετία του 1990 ανακαλύφθηκε ωστόσο ότι αυτά έχουν εξωγαλαξιακή προέλευση και συνδέονται με κάποια διεργασία στις σπείρες γαλαξιών. Πιθανό μοντέλο για τη δημιουργία των εκλάμψεων αποτελούν οι εκρήξεις υπερκαινοφανών υπερ-μαζικών άστρων ή η σύγκρουση δυο συμπαγών αστέρων (μελανών οπών ή αστέρων νετρονίων).

Η Κοσμική Ακτινοβολία αποτελείται από πυρήνες (πρωτόνια, σωμάτια άλφα, αλλά και βαρύτερους πυρήνες) οι οποίοι εισέρχονται στην ατμόσφαιρα της Γης με ρυθμό περίπου 1 σωμάτιο/cm2/sec [σχήμα 2.9]. Η πλειοψηφία αυτών των πυρήνων έχει σχετικιστικές ενέργειες, με ένα πολύ μικρό μέρος τους να φτάνει μέχρι ενέργειες 3 × 1020 eV που είναι και οι πιο υψηλές ενέργειες που έχουν ποτέ παρατηρηθεί. Τα σωμάτια της Κοσμικής Ακτινοβολίας, τουλάχιστον μέχρι κάποια ενέργεια, εισέρχονται ισοτροπικά στην ατμόσφαιρα της Γης. Παρόλο που η κοσμική ακτινοβολία είναι γνωστή από τις αρχές του 20ου αιώνα, η προέλευσή της εξακολουθεί να είναι άγνωστη. Σήμερα υπάρχουν ισχυρές ενδείξεις ότι η Κοσμική Ακτινοβολία μέχρι ενέργειες 1018 eV είναι Γαλαξιακής προέλευσης, ενώ τα σωματίδια πολύ υψηλών ενεργειών προέρχονται από εξωγαλαξιακές πηγές.
Το σχήμα 2.9 παρουσιάζει τη σύσταση των στοιχείων στην Κοσμική Ακτινοβολία και, για σύγκριση, την αντίστοιχη σύσταση στο Ηλιακό μας Σύστημα. Γενικά θα μπορούσαμε να πούμε ότι οι δύο αυτές κατανομές παρουσιάζουν ομοιότητες (π.χ. οι πυρήνες ϒδρογόνου αποτελούν σαφώς την πλειοψηφία και στις δύο περιπτώσεις), ωστόσο υπάρχουν και δύο βασικές διαφορές:
Καταρχάς οι πυρήνες με ατομικό αριθμό Ζ> 1 έχουν μεγαλύτερη αναλογία στην κοσμική ακτινοβολία από ότι στο Ηλιακό Σύστημα. Οι λόγοι που συμβαίνει αυτό δεν έχουν κατανοηθεί ακόμα. Θα μπορούσε, για παράδειγμα, ο μηχανισμός που επιταχύνει τα σωμάτια της κοσμικής ακτινοβολίας να δείχνει μία επιλεκτικότητα στους βαρύτερους πυρήνες ή ίσως η διαφορά αυτή να αντανακλά μία διαφορά στη σύσταση μεταξύ των (άγνωστων) πηγών της Κοσμικής Ακτινοβολίας και του Ηλιακού Συστήματος.
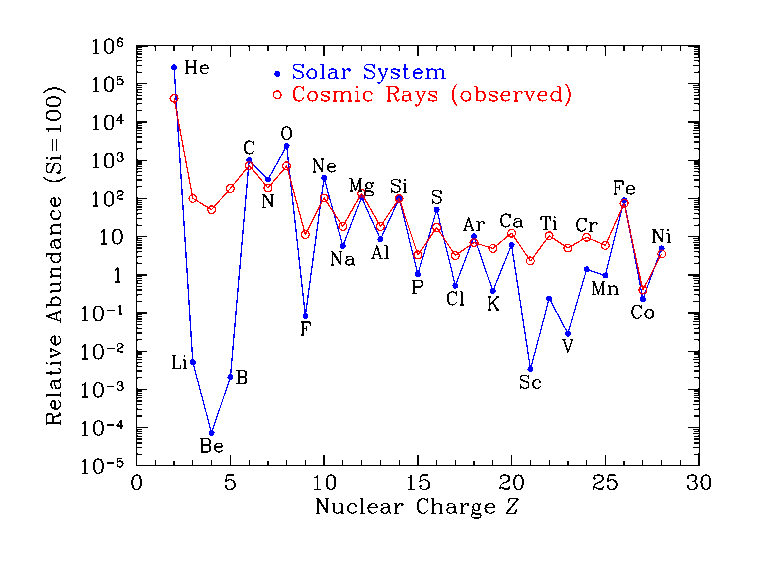
Η αιτία της άλλης διαφοράς έχει πλέον κατανοηθεί και αποτελεί πολύτιμο διαγνωστικό εργαλείο για τη διάδοση της κοσμικής ακτινοβολίας. Δύο ομάδες στοιχείων (Li, Be, B από τη μία και Sc, Ti, V, Cr, Mn από την άλλη) έχουν περιεκτικότητες που είναι πολλές τάξεις μεγέθους μεγαλύτερες στην κοσμική ακτινοβολία από ότι στο Ηλιακό Σύστημα [σχήμα 2.9]. Αυτά τα στοιχεία, σε αντίθεση με το ήλιο, τον άνθρακα ή το οξυγόνο, δεν ευνοούνται από την αστρική πυρηνοσύνθεση και υπάρχουν σε ελάχιστες ποσότητες στα άστρα και κατά συνέπεια και στο Ηλιακό μας Σύστημα. Ωστόσο αυτά τα στοιχεία απαντώνται στην Κοσμική Ακτινοβολία σε πολύ μεγαλύτερες αναλογίες επειδή δημιουργούνται από πυρηνικές αντιδράσεις θραύσεως των άφθονων πυρήνων άνθρακα και οξυγόνου (C, O→Li, Be, B) και σιδήρου (Fe →Sc, Ti, κλπ) καθώς αυτοί διαχέονται μέσα στον Γαλαξία μας. Επειδή γνωρίζουμε την ενεργό διατομή για τις παραπάνω αντιδράσεις καθώς και την πυκνότητα του μεσοαστρικού υλικού, μπορούμε να προσδιορίσουμε τις αποστάσεις τις οποίες οι πυρήνες πρέπει να έχουν διασχίσει από τη στιγμή της επιτάχυνσής τους έως τη στιγμή της παρατήρησής τους για να δημιουργήσουν τη μετρούμενη ποσότητα των θυγατρικών πυρήνων2 . Ο ιδιαίτερα απλός αυτός υπολογισμός φανερώνει ότι οι πυρήνες σιδήρου της κοσμικής ακτινοβολίας πρέπει να έχουν διασχίσει περί τα 1000 kpc μέσα στον Γαλαξία μας. Δοσμένου ότι ο Γαλαξίας έχει ακτίνα της τάξης των 10 kpc και πάχος μόλις 0.5 kpc, η ανωτέρω διαπίστωση σημαίνει ότι οι πυρήνες της κοσμικής ακτινοβολίας δεν κινούνται σε ευθύγραμμες τροχιές από τις όποιες πηγές τους, αλλά αντίθετα διαχέονται, εκτελούν δηλαδή ένα είδος τυχαίων κινήσεων παγιδευμένοι στην άλω και τον δίσκο του Γαλαξία. Η παγίδευση της κοσμικής ακτινοβολίας προέρχεται από το γεγονός ότι τα φορτισμένα σωματίδια στροβιλίζονται κατά μήκος των δυναμικών γραμμών του άμορφου μαγνητικού πεδίου του Γαλαξία ενώ ταυτόχρονα η γυροακτίνα τους είναι μικρότερη των διαστάσεων αυτού. Μόνον οι πυρήνες πολύ υψηλών ενεργειών έχουν γυροακτίνα μεγαλύτερη των διαστάσεων του Γαλαξία και για αυτόν τον λόγο θεωρούνται ότι είναι εξωγαλαξιακής προέλευσης.
Η ενεργειακή κατανομή των διαφόρων πυρήνων που απαρτίζουν την κοσμική
ακτινοβολία είναι νόμος δύναμης της μορφής 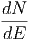 ∝ E-α όπου
∝ E-α όπου 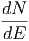 είναι η
ροή σωματιδίων όπως αυτή μετράται στη Γη (μονάδες: αριθμός σωματίων
ανά μονάδα επιφάνειας ανά μονάδα χρόνου ανά μονάδα ενέργειας). ΄Οπως
ίσως φαίνεται και από το σχήμα 2.10 η τιμή του δείκτη α παίρνει τις τιμές:
είναι η
ροή σωματιδίων όπως αυτή μετράται στη Γη (μονάδες: αριθμός σωματίων
ανά μονάδα επιφάνειας ανά μονάδα χρόνου ανά μονάδα ενέργειας). ΄Οπως
ίσως φαίνεται και από το σχήμα 2.10 η τιμή του δείκτη α παίρνει τις τιμές:
Η ενεργειακή πυκνότητα της κοσμικής ακτινοβολίας στον Γαλαξία μας υπολογίζεται από το ολοκλήρωμα
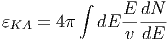 |
Μία δυσκολία στον υπολογισμό του παραπάνω ολοκληρώματος προέρχεται από το γεγονός ότι αυτό κυριαρχείται από το κάτω όριο και τούτο δεν μπορούμε να το μετρήσουμε με κάποια αξιοπιστία εξαιτίας της Ηλιακής διαμόρφωσης. Ο ηλιακός άνεμος απωθεί τα χαμηλής ενέργειας σωματίδια της κοσμικής ακτινοβολίας από την ηλιόσφαιρα. Η ένταση του ηλιακού ανέμου ακολουθεί τον ενδεκαετή κύκλο και, κατά συνέπεια, η μετρούμενη ροή της κοσμικής ακτινοβολίας διαμορφώνεται με αυτή. Στο μέγιστο του κύκλου όπου η ένταση του ηλιακού ανέμου είναι επίσης μέγιστη, η ροή της κοσμικής ακτινοβολίας είναι ελάχιστη και αντίθετα. Επειδή σε αυτές τις περιπτώσεις η ροή της κοσμικής ακτινοβολίας σχετικά χαμηλών ενεργειών (έως GeV) μπορεί να συμπιεσθεί και κατά μία τάξη μεγέθους, αυτό δημιουργεί προβλήματα στον ακριβή υπολογισμό του φάσματός της και φυσικά και στην ενεργειακή της πυκνότητα. Πρόσφατοι υπολογισμοί οι οποίοι προσπαθούν να αντιμετωπίσουν την παραπάνω δυσκολία με διάφορους τρόπους δίνουν τιμή για τα πρωτόνια 0.83 eV cm-3 ενώ για τα βαρύτερα σωμάτια (κυρίως πυρήνες Ηλίου) είναι 0.27 eV cm-3. Είναι χρήσιμο να συγκρίνουμε τις τιμές αυτές με την ενεργειακή πυκνότητα του γαλαξιακού μαγνητικού πεδίου (B ~ 3μGauss) που είναι 0.25 eV cm-3.
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press (3rd edition).
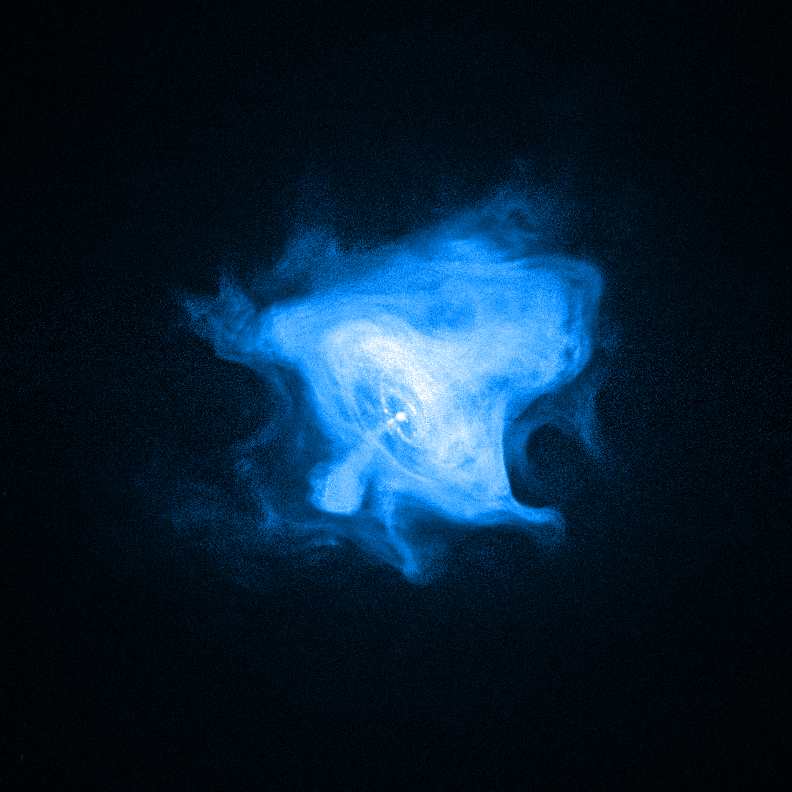
Το φάσμα της φωτεινής ενέργειας που εκπέμπουν οι αστέρες παράγεται και διαμορφώνεται στο εσωτερικό τους σύμφωνα με καλά καθορισμένους φυσικούς μηχανισμούς που εξαρτώνται από μια πληθώρα παραμέτρων όπως η πυκνότητα, η θερμοκρασία, ο βαθμός ιονισμού, η χημική σύσταση κ.α. Από την άλλη, οι αντίστοιχοι μηχανισμοί στην Αστροφυσική ϒψηλών Ενεργειών είναι διαφορετικής φύσεως και εξαρτώνται από παραμέτρους όπως η ενέργεια, η πυκνότητα και το είδος των σχετικιστικών σωματιδίων, το μαγνητικό πεδίο, κ.α. Γενικά οι μηχανισμοί που διαμορφώνουν τα αστροφυσικά φάσματα κατηγοριοποιούνται σε εκπομπής, απορρόφησης και σκεδασμού και παρουσιάζουν μεγάλη ποικιλία ανάλογα με τις φυσικές συνθήκες που επικρατούν στο υπό μελέτη αντικείμενο. Ωστόσο η μεθοδολογία υπολογισμού του εκπεμπόμενου φάσματος είναι σε όλες τις περιπτώσεις η ίδια και ανάγεται στην επίλυση μιας εξίσωσης η οποία διέπει τη διάδοση της ακτινοβολίας. Στο πρώτο μέρος λοιπόν του παρόντος Κεφαλαίου θα παρουσιάσουμε τις βασικές αρχές της επονομαζόμενης Εξίσωσης Διάδοσης Ακτινοβολίας (ΕΔΑ), η οποία μπορεί να εφαρμοσθεί σε οποιαδήποτε αστροφυσική πηγή, ενώ στο δεύτερο θα εστιάσουμε στις φυσικές διαδικασίες οι οποίες υπεισέρχονται σε αυτή και χαρακτηρίζουν τις αστροφυσικές πηγές υψηλών ενεργειών. Πιο συγκεκριμένα, θα αναφερθούμε σε εκείνες τις διαδικασίες οι οποίες διέπουν μία μη θερμική πηγή που περιέχει ηλεκτρόνια και πρωτόνια υψηλών ενεργειών και τα οποία αλληλεπιδρούν με μαγνητικά πεδία, χαμηλοενεργειακά φωτόνια και αραιό πλάσμα. Τέτοιες πηγές είναι οι πίδακες Ενεργών Γαλαξιών, οι εκλάμψεις ακτίνων γάμμα ή ακόμα, για να έρθουμε πιο κοντά στη Γη, και τα νεφελώματα ανέμων από pulsars όπως το Νεφέλωμα του Καρκίνου.
Θεωρούμε μία δέσμη ακτίνων φωτός που μεταφέρει ενέργεια dE ανά συχνότητα dν και διέρχεται κάθετα από επιφάνεια dA σε χρόνο dt και προς (ή από) στερεά γωνία dΩ [σχήμα 3.1]. Ορίζουμε την ειδική ένταση ακτινοβολίας Iν ως
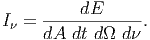 | (3.1) |
Ορίζουμε επίσης ως ροή ακτινοβολίας την ποσότητα
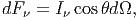 | (3.2) |
όπου θ είναι η γωνία που σχηματίζει η διεύθυνση της δέσμης με την κάθετη στην
επιφάνεια dA - βλ. σχήμα 3.2. Οι μονάδες της ροής είναι erg∕sec∕cm2∕Hz.
Η ολική ροή (ως προς όλες τις διευθύνσεις) είναι:
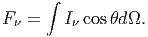 | (3.3) |
Εάν η Iν είναι ανεξάρτητη της γωνίας θ, τότε Fν = 0, δηλαδή όση ενέργεια
εισέρχεται στη στοιχειώδη επιφάνεια dA από τη διεύθυνση του 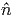 , άλλη
τόση εισέρχεται σε αυτή από τη διεύθυνση του -
, άλλη
τόση εισέρχεται σε αυτή από τη διεύθυνση του -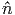 . Η πηγή τότε καλείται
ισοτροπική. Για παράδειγμα, στο εσωτερικό των αστέρων η ροή θα μπορούσε να
χαρακτηριστεί σε μεγάλο βαθμό ως ισοτροπική. Εάν η πηγή βρίσκεται σε μεγάλη
απόσταση D από τον παρατηρητή, τότε μπορούμε να γράψουμε από την
(3.3)
. Η πηγή τότε καλείται
ισοτροπική. Για παράδειγμα, στο εσωτερικό των αστέρων η ροή θα μπορούσε να
χαρακτηριστεί σε μεγάλο βαθμό ως ισοτροπική. Εάν η πηγή βρίσκεται σε μεγάλη
απόσταση D από τον παρατηρητή, τότε μπορούμε να γράψουμε από την
(3.3)
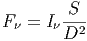 | (3.4) |
όπου S η επιφάνεια της πηγής.
Επιπλέον ορίζουμε τη διαφορική ενεργειακή πυκνότητα ακτινοβολίας uν ως
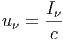 | (3.5) |
με μονάδες [uν] = erg∕cm3∕Hz∕sterad, ενώ τη διαφορική αριθμητική πυκνότητα
μπορούμε να τη βρούμε διαιρώντας το uν με hν.
Η ολική ενεργειακή πυκνότητα δίνεται από τη σχέση
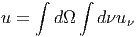 | (3.6) |
Η ΕΔΑ ουσιαστικά υπολογίζει την ειδική ένταση ακτινοβολίας σε ένα σημείο του χώρου εάν δίδονται οι μηχανισμοί εκπομπής, απορρόφησης και σκεδασμού. Στα παρακάτω θα εξετάσουμε αρχικά την εξίσωση σε κάποιες απλές περιπτώσεις, πριν προχωρήσουμε στο πιο πλήρες πρόβλημα.
΄Εστω ότι η πηγή περιέχει σωμάτια που εκπέμπουν ακτινοβολία με ενέργεια dE = jνdV dΩdtdν, όπου jν ο συντελεστής εκπομπής, με μονάδες erg/cm3/sec/Hz/sterad. Ο συντελεστής j ν ορίζεται από τις φυσικές διαδικασίες παραγωγής ακτινοβολίας της πηγής.
Σε αυτήν την περίπτωση η ΕΔΑ, η οποία περιγράφει τη μεταβολή του Iν κατά μήκος μιας δέσμης που διαδίδεται στον άξονα s, γράφεται
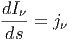 | (3.7) |
που έχει λύση
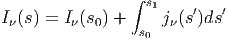 | (3.8) |
όπου s0 και s1 τα όρια της πηγής. Στην ειδική περίπτωση όπου το jν είναι ανεξάρτητο του s και Iν(s0) = 0, η ειδική ένταση ακτινοβολίας δίνεται από
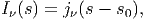 | (3.9) |
δηλαδή αυξάνεται γραμμικά με την απόσταση όσο η δέσμη διασχίζει την πηγή. Προφανώς για s > s1 προκύπτει Iν(s) = jν(s1 - s0), εφόσον υποθέσαμε ότι δεν υπάρχει εκπομπή ακτινοβολίας έξω από την πηγή.
΄Εστω n η αριθμητική πυκνότητα των απορροφητών κι έστω ότι ο καθένας χαρακτηρίζεται από ενεργό διατομή σν. Εάν θεωρήσουμε έναν στοιχειώδη όγκο dV = dAds τότε:
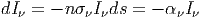 | (3.10) |
όπου ορίσαμε τον συντελεστή απορρόφησης αν = nσν (μονάδες cm-1). Αυτή είναι η ΕΔΑ στην περίπτωση όπου έχουμε μόνον απορρόφηση και η οποία έχει ως λύση
![[ ∫ s ]
Iν(s) = Iν(s0)exp - αν(s′)ds′
s0](HEA_files/HEA16x.png) | (3.11) |
Ορίζουμε ως οπτικό βάθος:
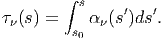 | (3.12) |
Στην περίπτωση όπου το αν είναι ανεξάρτητο του s και s1 -s0 = R, έχουμε [σχήμα
3.3]:
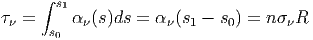 | (3.13) |
Παρατηρούμε ότι η ενέργεια της δέσμης φθίνει ως e-τν (σχεσεις 3.11 και 3.13). Συνεπώς εάν τν > 1 υπάρχει μεγάλη απορρόφηση της ενέργειας. Ορίζουμε λοιπόν το μέσο ως:
Τέλος ορίζουμε ως μέση ελεύθερη διαδρομή την απόσταση που διανύει
κατά μέσο όρο ένα φωτόνιο μέχρι να απορροφηθεί και τη συμβολίζουμε ως:
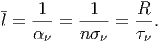 | (3.14) |
Παρατηρούμε ότι στην περίπτωση οπτικής αδιαφάνειας, η μέση ελεύθερη διαδρομή είναι μικρότερη της γραμμικής διάστασης της πηγής.
Εάν υποθέσουμε ότι στην πηγή υπάρχει και εκπομπή και απορρόφηση ακτινοβολίας, η ΕΔΑ γράφεται
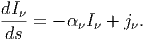 | (3.15) |
Ορίζουμε ως συνάρτηση πηγής την ποσότητα
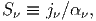 | (3.16) |
οπότε με τη χρήση της σχέσης (3.12) η σχέση (3.15) γίνεται
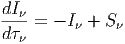 | (3.17) |
Η παραπάνω έχει γενική λύση:
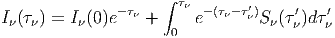 | (3.18) |
Στην περίπτωση όπου το Sν είναι ανεξάρτητο του τν, η (3.18) γράφεται
![Iν(τν) = Sν + e-τν [Iν(0) - Sν]](HEA_files/HEA24x.png) | (3.19) |
Εάν επιπλέον τν →∞, η (3.19) δίνει Iν → Sν, δηλαδή η ειδική ένταση ακτινοβολίας
τείνει στη συνάρτηση πηγής.
Νόμος του Kirchoff: ΄Οταν ύλη και ακτινοβολία βρίσκονται σε θερμοδυναμική ισορροπία, οι συντελεστές εκπομπής και απορρόφησης συνδέονται με τη σχέση
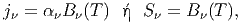 | (3.20) |
όπου Bν(T) = 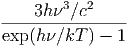 η συνάρτηση Planck που περιγράφει την
ακτινοβολία μέλανος σώματος.
η συνάρτηση Planck που περιγράφει την
ακτινοβολία μέλανος σώματος.
Από την (3.19) προκύπτει ότι για Iν(0) = 0
΄Εστω ότι σε ένα μέσο έχουμε μόνον σκεδασμούς που επιπλέον είναι ισοτροπικοί και ελαστικοί. Σε αναλογία με την περίπτωση εκπομπής ορίζουμε ως συντελεστή «εκπομπής»:
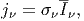 | (3.21) |
όπου Iν = 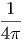 ∫
IνdΩ η μέση ειδική ένταση ακτινοβολίας και σν ο συντελεστής
σκεδασμού.
∫
IνdΩ η μέση ειδική ένταση ακτινοβολίας και σν ο συντελεστής
σκεδασμού.
Η σχέση (3.21) υποδηλώνει ότι η ενέργεια δεν παράγεται κατά μήκος της δέσμης,
όπως στην περίπτωση των μηχανισμών εκπομπής, παρά εισέρχεται σε αυτή από τους
σκεδασμούς που πραγματοποιούνται κατά μέσο όρο σε όλες τις υπόλοιπες
δέσμες που διασχίζουν την πηγή. Συνεπώς, αυτή η διαδικασία συντελεί
στο να κερδίζει η δέσμη ενέργεια. Από την άλλη, οι σκεδασμοί μπορούν να
αφαιρούν ενέργεια από τη δέσμη, δρώντας ουσιαστικά ως «απορρόφηση», με την
ενέργεια να μην απορροφάται, αλλά να εκτρέπεται από τη δέσμη. Η ΕΔΑ
γράφεται:
![dI -- [ 1 ∫ ]
--ν-= - σ ν(Iν - Iν) = - σν Iν - --- IνdΩ
ds 4π](HEA_files/HEA29x.png) | (3.22) |
όπου ο πρώτος όρος στο δεξί μέλος παίζει τον ρόλο της απορρόφησης και ο δεύτερος της εκπομπής. Αυτή είναι μία ολοκληροδιαφορική εξίσωση η οποία είναι δύσκολο να επιλυθεί. Τέλος, όταν η πηγή έχει και τις τρεις προαναφερθείσες διαδικασίες, δηλαδή εκπομπή, απορρόφηση κα σκεδασμό, η ΕΔΑ γράφεται:
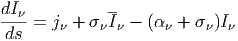 | (3.23) |
που μπορεί να επιλυθεί μόνο μετά από κατάλληλες προσεγγίσεις ή αριθμητικά.
Σε αυτή την ενότητα θα αναφερθούμε σύντομα στις κυριότερες από τις φυσικές διαδικασίες της ΑϒΕ που συνεισφέρουν στην εκπομπή, απορρόφηση και σκεδασμό της ακτινοβολίας. Η σημαντικότερη αλληλεπίδραση φωτονίου - ηλεκτρονίου είναι ο γνωστός σκεδασμός Compton. Ωστόσο αυτός αφορά την αλληλεπίδραση ενεργητικού φωτονίου με ακίνητο ηλεκτρόνιο. Στην περίπτωσή μας ενδιαφερόμαστε για το αντίστροφο πρόβλημα, δηλαδή το αποτέλεσμα της αλληλεπίδρασης σχετικιστικών ηλεκτρονίων με φωτόνια χαμηλών ενεργειών. Κατά τη φυσική αυτή διαδικασία τα ηλεκτρόνια χάνουν ενέργεια που την κερδίζουν τα φωτόνια τα οποία και σκεδάζονται σε υψηλές ενέργειες. Ο μηχανισμός θεωρείται υπεύθυνος για τη δημιουργία φασμάτων εκπομπής υψηλών ενεργειών, όπως π.χ. για την παρατηρούμενη ακτινοβολία γ από πίδακες ενεργών γαλαξιών, για την παραγωγή της διάχυτης ακτινοβολίας γ από τον δίσκο του Γαλαξία μας κλπ. Λόγω της μεγάλης σπουδαιότητάς του για την Αστροφυσική ϒψηλών Ενεργειών θα αναφερθούμε διεξοδικά σε αυτόν στο Κεφάλαιο 5. Σημειώνουμε ότι παρόλο που τυπικά πρόκειται για σκεδασμό, ουσιαστικά λειτουργεί ως μηχανισμός εκπομπής ενεργητικών φωτονίων καθώς έχει την ιδιότητα να σκεδάζει φωτόνια χαμηλών ενεργειών σε φωτόνια υψηλών ενεργειών.
Πρόκειται για την ακτινοβολία που παράγουν ηλεκτρόνια υψηλών ενεργειών επιταχυνόμενα σε μαγνητικά πεδία. Πρόκειται για έναν σημαντικότατο μηχανισμό με μία πληθώρα αστροφυσικών εφαρμογών. Ενδεικτικά αναφέρουμε ότι η ραδιοεκπομπή από τον δίσκο του Γαλαξία μας, από τα κελύφη των υπερκαινοφανών, από τους πυρήνες, πίδακες και ραδιολοβούς των ενεργών γαλαξιών αποδίδεται σε αυτόν. Θα τον εξετάσουμε στο κεφάλαιο 6. Φυσικά πρόκειται για μηχανισμό εκπομπής ακτινοβολίας.
Η ακτινοβολία πέδης (bremsstrahlung) είναι η ακτινοβολία που δημιουργείται από την επιτάχυνση ηλεκτρονίων από πυρήνες λόγω των δυνάμεων Coulomb. ΄Εχει πολλές εφαρμογές στην αστροφυσική, από τα εσωτερικά των αστέρων (η γνωστή διαδικασία free-free) έως την παραγωγή ακτίνων γ από τις ηλιακές εκλάμψεις. Ωστόσο η εφαρμογή της σε πηγές υψηλών ενεργειών είναι περιορισμένη, κυρίως γιατί σε αυτές το πλάσμα είναι πολύ αραιό με αποτέλεσμα να επικρατούν ως μηχανισμοί ακτινοβολίας των σχετικιστικών ηλεκτρονίων η σύγχροτρον και ο αντίστροφος μηχανισμός Compton.
Τα πρωτόνια είναι από τη μία σωμάτια με ηλεκτρικό φορτίο και συνεπώς υπόκεινται σε ανάλογους με τα ηλεκτρόνια φυσικούς μηχανισμούς, είναι όμως και αδρόνια και υπόκεινται σε μια σειρά αδρονικών αλληλεπιδράσεων. Εδώ παρουσιάζουμε τις κυριότερες, από πλευράς αστροφυσικών εφαρμογών:
΄Οταν η κινητική ενέργεια του πρωτονίου υψηλής ενέργειας είναι μεγαλύτερη της μάζας ηρεμίας του πιονίου, τότε μία σύγκρουση πρωτονίου-πρωτονίου δημιουργεί πιόνια τα οποία διασπώνται ανάλογα του είδους τους (ουδέτερα ή φορτισμένα) σε φωτόνια ή σε μιόνια και νετρίνα, σύμφωνα με τις αντιδράσεις
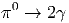 |
και
| π+ → μ+ + ν μ | ||
| π- → μ- + ν μ. |
Τα ουδέτερα πιόνια έχουν έναν πολύ σύντομο μέσο χρόνο ζωής (1.8 × 10-16sec) πριν διασπασθούν σε δύο φωτόνια που ουσιαστικά είναι ακτίνες γ, ενώ τα φορτισμένα πιόνια έχουν μέσο χρόνο ζωής 2.6 × 10-8sec πριν διασπασθούν σε μιόνια. Τέλος τα μιόνια χαμηλής ενέργειας διασπώνται μετά από 2.2 × 10-6sec σε ηλεκτρόνια, ποζιτρόνια και νετρίνα:
| μ+ → e+ + ν e + νμ | ||
| μ- → e- + ν e + νμ |
΄Ολες οι παραπάνω αλληλεπιδράσεις πραγματοποιούνται, για παράδειγμα, στον μεσογαλαξιακό χώρο καθώς τα ενεργητικά πρωτόνια της κοσμικής ακτινοβολίας αλληλεπιδρούν με το ψυχρό αέριο του Γαλαξιακού δίσκου.
Η αλληλεπίδραση πρωτονίων υψηλών ενεργειών και φωτονίων (ή, αντίστοιχα,
ακτίνων γ και ψυχρών πρωτονίων) μπορεί να είναι είτε ηλεκτρομαγνητικής είτε
αδρονικής φύσεως:
α. Παραγωγή ζεύγους ηλεκτρονίου-ποζιτρονίου (pγ → pe+e-)
β. Παραγωγή πιονίων (pγ → Nπ, όπου N πρωτόνιο ή νετρόνιο)
Η διαδικασία (α) έχει κατώφλι το άθροισμα των μαζών ηρεμίας του ζεύγους.
Η διαδικασία (β) έχει άμεση αντιστοιχία με τη διαδικασία αλληλεπίδρασης
πρωτονίου-πρωτονίου. ΄Ετσι όταν η ενέργεια του φωτονίου στο σύστημα ηρεμίας του
πρωτονίου υπερβαίνει τη μάζα ηρεμίας του πιονίου, τότε δημιουργούνται πιόνια ενώ
τα πρωτόνια χάνουν μέρος της ενέργειάς τους. Η διαδικασία αυτή έχει εφαρμογή
στην κοσμική ακτινοβολία πολύ υψηλών ενεργειών.
Αυτή η διαδικασία είναι γνωστή στην Αστροφυσική και από το εσωτερικό των αστέρων. Τα φωτόνια απορροφώνται από τα άτομα είτε ιονίζοντας είτε διεγείροντάς τα. Επειδή ο συντελεστής απορρόφησης μειώνεται γρήγορα με τη συχνότητα του φωτονίου (αν ∝ ν-3), η διαδικασία αυτή βρίσκει αστροφυσική εφαρμογή σε ακτινοβολία έως και τις ακτίνες Χ. Αυτό κάνει την παραπάνω διαδικασία μικρής μάλλον σημασίας για τις πηγές ακτίνων γ ενώ αντίθετα αυτή παίζει σημαντικό ρόλο στη διαμόρφωση του φάσματος στις πηγές ακτίνων Χ.
Ο σκεδασμός Compton παρουσιάζει ιδιαίτερο αστροφυσικό ενδιαφέρον στις περιπτώσεις εκείνες όπου το οπτικό βάθος της πηγής στον σκεδασμό είναι μεγάλο. Σε αυτήν την περίπτωση τα φωτόνια υφίστανται πολλαπλές σκεδάσεις από τα ηλεκτρόνια καθώς η μέση ελεύθερη διαδρομή είναι πολύ μικρότερη από τις διαστάσεις της πηγής. Η διαδικασία βρίσκει εφαρμογες στο εσωτερικό των αστέρων και στους δίσκους προσαύξησης αλλά έχει περιορισμένες εφαρμογές στις πηγές ακτίνων γ.
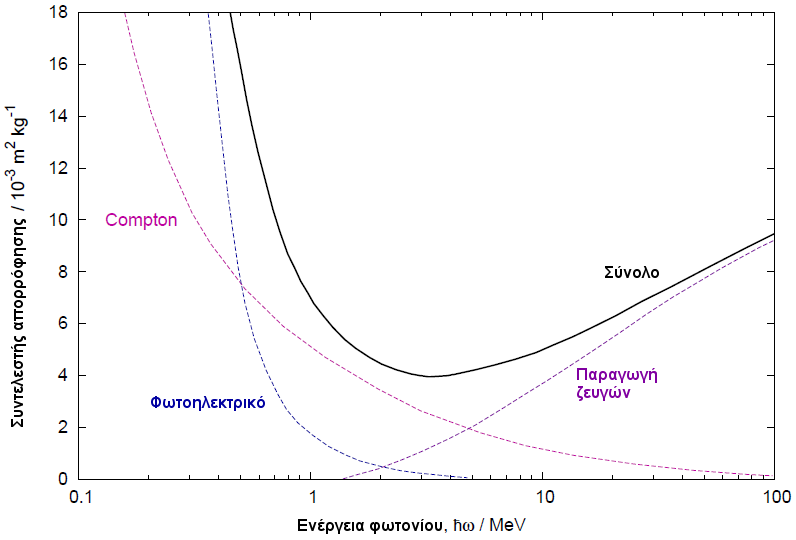
Εάν η ενέργεια του φωτονίου ξεπερνάει τη μάζα ηρεμίας ηλεκτρονίου-ποζιτρονίου, τότε είναι δυνατόν το φωτόνιο να απορροφηθεί παράγοντας ένα τέτοιο ζεύγος. Η διαδικασία αυτή έχει σχετικά μικρή ενεργό διατομή, ωστόσο μπορεί να επικρατήσει του σκεδασμού Compton ή της φωτοηλεκτρικής απορρόφησης για αρκετά μεγάλες ενέργειες του φωτονίου [σχήμα 3.4]. Για παράδειγμα, αυτός είναι ο κύριος μηχανισμός απορρόφησης των ακτίνων γ όταν αυτές εισέρχονται στην ατμόσφαιρα της Γης.
Ακτίνες γ μπορούν να αλληλεπιδράσουν με άλλα φωτόνια προς παραγωγή ζεύγους ηλεκτρονίου-ποζιτρονίου. Πρόκειται για έναν πολύ σημαντικό μηχανισμό απορρόφησης ενεργητικών φωτονίων που θα εξετάσουμε διεξοδικά στο Κεφάλαιο 4 και αφορά ουσιαστικά όλες τις πηγές ακτίνων γ.
Πρόκειται για τη διαδικασία κατά την οποία φωτόνια υψηλών ενεργειών παράγουν ζεύγη ηλεκτρονίων-ποζιτρονίων καθώς διασχίζουν μαγνητικές δυναμικές γραμμές. Η διαδικασία έχει προς το παρόν προταθεί σε προβλήματα διάδοσης ακτινοβολίας στις μαγνητόσφαιρες των pulsars καθώς, για να ικανοποιηθεί η συνθήκη κατωφλίου της, απαιτείται η παρουσία πολύ ισχυρών μαγνητικών πεδίων.
Θεωρούμε σφαιρική πηγή τα σωμάτια της οποίας εκπέμπουν με συντελεστή
εκπομπής jν (μονάδες ενέργεια/χρόνο/συχνότητα). Η πηγή απέχει απόσταση
D από τη Γη, έχει ακτίνα R και τα σωμάτια αυτής έχουν πυκνότητα n.
(i) Θεωρώντας ότι η πηγή είναι οπτικά διαφανής και ομογενής να υπολογίσετε
την ειδική ένταση ακτινοβολίας Iν ως συνάρτηση της γωνίας θ (η γωνία θ = 0
αντιστοιχεί στην ευθεία Γη-κέντρο της πηγής).
(ii) Να επαναλάβετε τους παραπάνω υπολογισμούς αν ισχύει n(r) =
n0(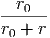 )β, 0 < r < R.
)β, 0 < r < R.
(iii) Ποια είναι η ροή ακτινοβολίας και η ολική λαμπρότητα της πηγής στην
περίπτωση (i);
(Εφαρμογή: D = 3 kpc, R = 1 pc, r0 = 0.01 pc, β = 2.)
Πηγή πάχους D χαρακτηρίζεται από συντελεστή εκπομπής:
jν = Aν-1 για ν min ≤ ν ≤ νmax και jν = 0 για ν < νmin και ν > νmax.
Ο συντελεστής απορρόφησης είναι αν = B[(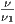 )2 - 1] για ν
1 ≤ ν ≤ νmax (όπου
νmin < ν1) και αν = 0 για όλες τις άλλες συχνότητες (Α, Β σταθερές). Ποια η ροή
που παρατηρούμε σε απόσταση D από τη πηγή;
)2 - 1] για ν
1 ≤ ν ≤ νmax (όπου
νmin < ν1) και αν = 0 για όλες τις άλλες συχνότητες (Α, Β σταθερές). Ποια η ροή
που παρατηρούμε σε απόσταση D από τη πηγή;
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press
(3rd edition).
Rybicki, B. G. & Lightman, P. A., (1985), Radiative Processes in Astrophysics.
Wiley.
΄Οπως αναφέραμε στο προηγούμενο Κεφάλαιο, η αλληλεπίδραση φωτονίου-φωτονίου
προς παραγωγή ζεύγους ηλεκτρονίου-ποζιτρονίου αποτελεί μία από τις βασικές
διαδικασίες της Αστροφυσικής ϒψηλών Ενεργειών. Παρακάτω δίνουμε,
ως παράδειγμα, μία πληρέστερη ανάλυση αυτής της διαδικασίας ώστε να
εφαρμοστούν οι έννοιες της ενέργειας κατωφλίου, της ενεργού διατομής και του
οπτικού βάθους, βλ. παράγραφο 3.1.2. Για να βρούμε το ενεργειακό κατώφλι
παραγωγής του ζεύγους εργαζόμαστε ως εξής: ΄Εστω K 1 = ![[ ]
h-ν1, hν1-^e1
c c](HEA_files/HEA34x.png) και
K2 =
και
K2 = ![[ ]
h ν2 hν2
-c--,-c--^e2](HEA_files/HEA35x.png) τα τετρανύσματα ορμής των φωτονίων πριν από τη σύγκρουση.
Εάν P 1 = [γ1mec,γ1meu1] και P 2 = [γ2mec,γ2meu2] είναι τα τετρανύσματα ορμής
των δύο παραγόμενων σωματίων, τότε από τη διατήρηση των μεγεθών αυτών
έχουμε:
τα τετρανύσματα ορμής των φωτονίων πριν από τη σύγκρουση.
Εάν P 1 = [γ1mec,γ1meu1] και P 2 = [γ2mec,γ2meu2] είναι τα τετρανύσματα ορμής
των δύο παραγόμενων σωματίων, τότε από τη διατήρηση των μεγεθών αυτών
έχουμε:
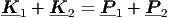 | (4.1) |
Η ελάχιστη ενέργεια με την οποία μπορεί να παραχθεί το ζεύγος είναι όταν u1 = u2 = 0 και συνεπώς P 1 = [mec, 0], P 2 = [mec, 0]. ϒψώνουμε στο τετράγωνο και τα δύο μέλη της παραπάνω εξίσωσης και χρησιμοποιώντας τις γνωστές σχέσεις K 1 ⋅K 1 = K 2 ⋅K 2 = 0 και P 1 ⋅P 1 = P 2 ⋅P 2 = P 1 ⋅P 2 = 2mec2 παίρνουμε
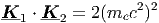 |
η οποία, μετά από μερικές πράξεις, γράφεται
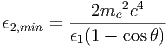 | (4.2) |
όπου ϵ1 = hν1 και ϵ2 = hν2 είναι οι ενέργειες των δύο φωτονίων και θ η γωνία που
σχηματίζουν οι διευθύνσεις τους.
Η σχέση (4.2) δίνει την ελάχιστη ενέργεια ϵ2 που απαιτείται να έχει
ένα φωτόνιο ώστε να δημιουργήσει ζεύγος ηλεκτρονίου-ποζιτρονίου όταν
αλληλεπιδρά υπό γωνία θ με άλλο φωτόνιο ενέργειας ϵ1. Αυτό είναι και το
ενεργειακό κατώφλι της παραπάνω φυσικής διαδικασίας. Η διαδικασία αυτή
δεν δρα μόνον ως μηχανισμός παραγωγής ζευγών αλλά και ως μηχανισμός
απορρόφησης ακτίνων γ. Θα μπορούσαμε λοιπόν, ξαναγυρίζοντας προς στιγμή
στην Αστροφυσική, να θεωρήσουμε μερικές χαρακτηριστικές ενέργειες
χαμηλοενεργειακών φωτονίων (ϵ1) και με τη βοήθεια της σχέσης (4.2) να βρούμε την
απαιτούμενη ελάχιστη ενέργεια (ϵ2,min) που πρέπει να έχουν οι ακτίνες γ ώστε να
αλληλεπιδράσουν με αυτά. Τα σχετικά αποτελέσματα δίνονται στον πίνακα 4.1 όπου
για χάρη απλότητας θεωρήσαμε θ = π (δηλαδή μετωπικές συγκρούσεις).
|
| ϵ1 (eV) | ϵ2,min (eV) |
| Κοσμικό υπόβαθρο μικροκυμάτων | 6 × 10-4 | 4 × 1014 |
| Αστέρες | 2 | 1011 |
| Πηγές ακτίνων Χ | 103 | 3 × 108 |
|
|
Καταρχήν παρατηρούμε ότι οι ενέργειες των φωτονίων που θα μπορούσαν να
απορροφηθούν βρίσκονται όντως στην περιοχή των ακτίνων γ. Ωστόσο για να είναι η
απορρόφηση των ακτίνων γ σημαντική πρέπει αυτά να έχουν και μεγάλο οπτικό βάθος ως προς απορρόφηση. Η έννοια του οπτικού βάθους είναι γνωστή από άλλους
τομείς της Αστροφυσικής (πχ. αστρικές ατμόσφαιρες) αλλά και της Φυσικής
γενικότερα - βλ. σχέση 3.12.
Στην περίπτωση της απορρόφησης φωτονίου-φωτονίου, αυτό δίνεται από τη σχέση:
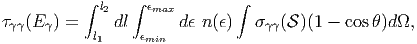 | (4.3) |
όπου Eγ η ενέργεια της ακτίνας γ, l1 και l2 τα όρια της περιοχής την οποία αυτή
διασχίζει και n(ϵ) η διαφορική αριθμητική πυκνότητα [μονάδες: αριθμός
φωτονίων/όγκο/ενέργεια (ή συχνότητα) φωτονίου] των χαμηλοενεργειακών
φωτονίων-στόχων τα οποία έχουν κατανομή μεταξύ των ενεργειών ϵmin < ϵ < ϵmax.
Τέλος, σγγ η ενεργός διατομή της διαδικασίας και S = Eγϵ(1 - cos θ).
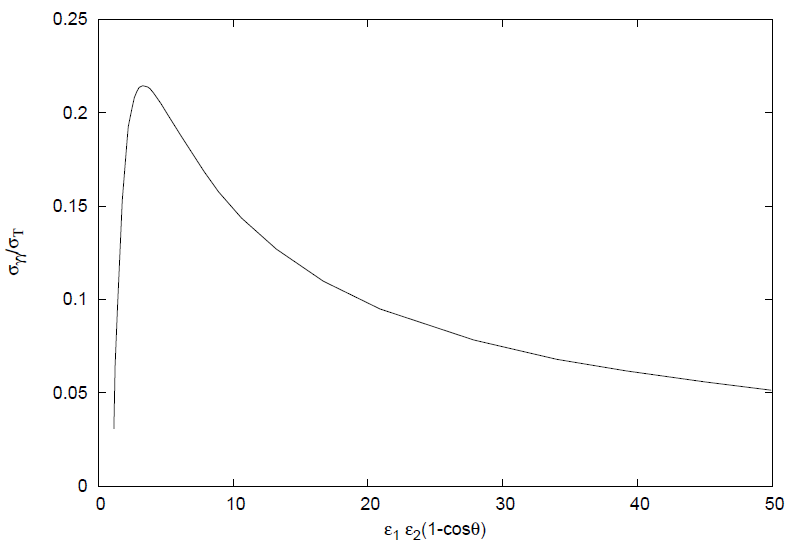
Η ενεργός διατομή υπολογίζεται από την Κβαντική Ηλεκτροδυναμική και
παριστάνεται γραφικά στο σχήμα 4.1. Παρατηρούμε ότι για τιμές του γινομένου
S = ϵ1ϵ2(1 - cos θ) < 2(mec2)2 η ενεργός διατομή σ
γγ είναι μηδέν, σε συμφωνία με
τα όσα αναφέραμε για το ενεργειακό κατώφλι της συγκεκριμένης φυσικής
αλληλεπίδρασης. Για τιμές του S λίγο πάνω από το ενεργειακό κατώφλι η ενεργός
διατομή αυξάνεται απότομα μέχρι μία μέγιστη τιμή σγγmax ≃ 0.22σ
T , όπου σT είναι η
ενεργός διατομή Thomson (βλ. κεφάλαιο 5) και από εκεί και πέρα φθίνει περίπου ως
S-1.
Παρατηρούμε ότι η σχέση (4.3) αποτελεί γενίκευση της σχέσης (3.12), καθώς οι
στόχοι, επειδή είναι φωτόνια, έχουν και κατανομή ως προς ενέργειες και
διεύθυνση. Επιβάλλεται λοιπόν να ολοκληρώσουμε το οπτικό βάθος ως
προς ενέργεια των φωτονίων-στόχων και ως προς στερεά γωνία. Τέλος,
σημειώνουμε ότι ο όρος (1 - cos θ) στο παραπάνω ολοκλήρωμα είναι κινηματικής
προέλευσης και υποδηλώνει ότι οι πιο πιθανές αλληλεπιδράσεις της ακτίνας
γ είναι με φωτόνια που έχουν αντίθετη διεύθυνση (θ = π). Αντίθετα, η
αλληλεπίδραση είναι αδύνατη εάν η διεύθυνση των δύο φωτονίων έχει την ίδια φορά.
΄Ενα χαρακτηριστικό παράδειγμα αποτελεί η απορρόφηση φωτονίων υψηλών ενεργειών από τα φωτόνια του κοσμικού μικροκυματικού υπόβαθρου. Επειδή αυτά περιγράφονται από κατανομή μέλανος σώματος η αριθμητική τους πυκνότητα ως προς ενέργεια εξαρτάται μόνο από τη θερμοκρασία της ακτινοβολίας και δίνεται από τη σχέση:
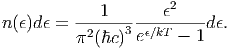 | (4.4) |
Σε αυτήν την περίπτωση έχει μεγαλύτερη φυσική σημασία να υπολογίσουμε τη
μέση ελεύθερη διαδρομή που μας δίνει κατά μέσο όρο την απόσταση που έχει
διανύσει έως τη Γη κάποιο φωτόνιο υψηλών ενεργειών χωρίς να έχει απορροφηθεί
από τα φωτόνια του υπόβαθρου. Το σχήμα 4.2 παριστάνει ακριβώς αυτό ως
συνάρτηση της ενέργειας της ακτίνας γ. Παρατηρούμε ότι για ενέργειες
Eγ ≤ 105GeV = 1014eV το Σύμπαν είναι διαφανές. Για μεγαλύτερες όμως ενέργειες
οι ακτίνες γ απορροφώνται από τα φωτόνια του υπόβαθρου και για ενέργειες
Eγ = 1015eV η μέση ελεύθερη διαδρομή είναι της τάξης των 10 kpc, κάτι που
πρακτικά σημαίνει ότι εάν ποτέ παρατηρηθούν ακτίνες γ τέτοιων ενεργειών αυτές
πρέπει να προέρχονται από πηγή του Γαλαξία μας και όχι από κοσμολογικές πηγές
(όπως π.χ. οι quasars). Για ακόμα μεγαλύτερες ενέργειες η μέση ελεύθερη
διαδρομή αυξάνεται και αυτό οφείλεται στην πτώση της ενεργού διατομής [βλ.
και σχήμα 4.1] αλλά και στη συγκεκριμένη μορφή (4.4) του πεδίου των
φωτονίων.
Το παραπάνω αποτελεί ένα μόνο παράδειγμα της απορρόφησης ακτίνων γ από
φωτόνια χαμηλότερης ενέργειας. ΄Αλλα παραδείγματα περιλαμβάνουν αστροφυσικές
πηγές ακτίνων γ όπως pulsars, ενεργούς γαλαξίες, κλπ. Σε αυτές τις περιπτώσεις
εξετάζουμε την πιθανότητα που έχει μία ακτίνα γ να απορροφηθεί μέσα στην
ίδια την πηγή από άλλα φωτόνια χαμηλότερης ενέργειας. Τέτοιου είδους
υπολογισμοί αποτελούν πολύτιμα διαγνωστικά για τις ιδιότητες των πηγών
αυτών.
Το κατώφλι για αλληλεπιδράσεις φωτονίου-φωτονίου δίνεται από τη σχέση
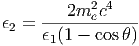 |
όπου θ είναι η γωνία που σχηματίζουν οι διευθύνσεις των δύο σωματιδίων.
A. Θεωρώντας κατά μέτωπο αλληλεπιδράσεις, να αντιστοιχίσετε τις παρακάτω
ενέργειες σε ζεύγη που μπορούν να παράγουν ζεύγη ηλεκτρονίων-ποζιτρονίων.
α) Μικροκυματική ακτινοβολία υποβάθρου, ενέργειας 600 μeV
β) ϒπέρυθρη εκπομπή γαλαξιακής σκόνης, ενέργειας 10 meV
γ) ϒπεριώδης ακτινοβολία αστέρα, ενέργειας 10 eV
δ) Μαλακές ακτίνες Χ ενέργειας 1 keV
ε) Σκληρές ακτίνες Χ ενέργειας 0.05 MeV
στ) Ακτίνες γ ενέργειας 1 GeV
ζ) Ακτίνες γ ενέργειας 4 TeV
η) Ακτίνες γ ενέργειας 1 PeV
1) Ακτίνες γ ενέργειας 1 PeV
2) Ακτίνες γ ενέργειας 4 TeV
3) Ακτίνες γ ενέργειας 1 GeV
4) Σκληρές ακτίνες Χ ενέργειας 0.05 MeV
5) Μαλακές ακτίνες Χ ενέργειας 1 keV
6) ϒπεριώδης ακτινοβολία αστέρα, ενέργειας 10 eV
7) ϒπέρυθρη εκπομπή γαλαξιακής σκόνης, ενέργειας 10 meV
8) Μικροκυματική ακτινοβολία υποβάθρου, ενέργειας 600 μeV
B. ΄Οταν υπερκαλύπτεται η συνθήκη κατωφλίου κατά πολλές τάξεις μεγέθους, η αλληλεπίδραση είναι το ίδιο εύκολη με όταν η συνθήκη κατωφλίου οριακά καλύπτεται, περισσότερο εύκολη ή λιγότερο εύκολη; Ποιοι παράγοντες το καθορίζουν;
A. Θεωρήστε έναν σφαιρικό όγκο V 0 (ακτίνας r0) ο οποίος περιέχει ακτινοβολία. ϒποθέτουμε ότι σε κάθε χρονική στιγμή το σύστημα βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας. Επομένως, η ακτινοβολία ακολουθεί τον νόμο του Planck για δεδομένη θερμοκρασία T0:
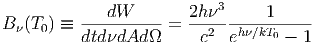 |
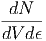 .
.
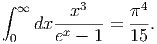 |
ϒπάρχει άλλος τρόπος για τον υπολογισμό της ποσότητας αυτής;
B. Θέλουμε να υπολογίσουμε την πιθανότητα ένα φωτόνιο ενέργειας Eγ να απορροφηθεί από την κατανομή φωτονίων του μελανού σώματος n(ϵ). Με άλλα λόγια θέλουμε να υπολογίσουμε το οπτικό βάθος, το οποίο απλοποιείται στην περίπτωση όπου τα χαμηλοενεργειακά φωτόνια έχουν ισοτροπική κατανομή ως εξής:
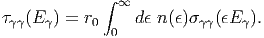 |
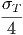
 Θ(y - 1), όπου Θ(x) = 0, x < 0 και Θ(x) = 1, x > 0 (Οι
μεταβλητές x,y είναι αδιάστατες). Σας δίνεται επίσης το ολοκλήρωμα
Θ(y - 1), όπου Θ(x) = 0, x < 0 και Θ(x) = 1, x > 0 (Οι
μεταβλητές x,y είναι αδιάστατες). Σας δίνεται επίσης το ολοκλήρωμα
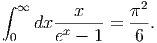 |
G. Ας υποθέσουμε ότι ο σφαιρικός όγκος του προηγούμενου ερωτήματος εκτονώνεται αδιαβατικά, δηλαδή με τέτοιο τρόπο ώστε να μην ανταλλάσσει θερμότητα με το περιβάλλον. Η ακτινοβολία κατά την αδιαβατική μεταβολή συμπεριφέρεται ως «αέριο» φωτονίων με αδιαβατικό δείκτη γ = 4∕3. Η αρχική ακτίνα r0 και θερμοκρασία T0 θεωρούνται γνωστά.
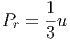 |
να βρείτε τη θερμοκρασία του μελανού σώματος ως συνάρτηση της ακτίνας, T(r). Εκφράστε το οπτικό βάθος που βρήκατε σε προηγούμενο ερώτημα ως συνάρτηση του r. ϒπολογίστε την ακτίνα r1 στην οποία το οπτικό βάθος γίνεται μονάδα.
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press
(3rd edition).
Gould, R. J. & Schreder, G. P. (1967). “Opacity of the Universe to High-Energy
Photons”. Physical Review, vol. 155, Issue 5, pp. 1408-1411.
Protheroe, R. J. (1986). “Effect of electron-photon cascading on the observed
energy spectra of extragalactic sources of ultra-high-energy gamma-rays”. Monthly
Notices of the Royal Astronomical Society (ISSN 0035-8711), Vol. 221, Aug. 15,
1986, p. 769-788.
Gould, R. J. & Schreder, G. (1966). “Opacity of the Universe to High-Energy
Photons”. Physical Review Letters, vol. 16, Issue 6, pp. 252-254.
΄Οπως είναι γνωστό ο Compton ανακάλυψε το 1923 ότι το μήκος κύματος των
σκληρών ακτίνων Χ αυξάνεται όταν αυτές σκεδάζονται από ηλεκτρόνια σε ηρεμία.
Αυτό ήρθε ως μία ακόμη επιβεβαίωση της κβαντικής θεωρίας του Einstein για τον
δυϊσμό της φύσης του φωτός. Κατά τον σκεδασμό Compton το εισερχόμενο
φωτόνιο συγκρούεται με το ακίνητο ηλεκτρόνιο και του μεταφέρει μέρος της
ενέργειας και της ορμής του. Επειδή και τα δύο αυτά μεγέθη εξαρτώνται από τη
συχνότητα της ακτινοβολίας, η απώλεια ενέργειας του φωτονίου αντιστοιχεί στη
μετρούμενη αύξηση του μήκους κύματός του. Μεγάλο ενδιαφέρον για την
Αστροφυσική ϒψηλών Ενεργειών παρουσιάζει η περίπτωση όπου σχετικιστικά
ηλεκτρόνια σκεδάζουν φωτόνια χαμηλής ενέργειας σε υψηλές ενέργειες.
Αυτή η διαδικασία ονομάζεται αντίστροφος σκεδασμός Compton γιατί σε
αυτήν την περίπτωση είναι τα ηλεκτρόνια που χάνουν ενέργεια αντί για τα
φωτόνια.
Θα ξεκινήσουμε το Κεφάλαιο με σύντομες αναφορές στο κλασικό φαινόμενο
Thomson και στον σκεδασμό Compton. Στη συνέχεια θα αναπτύξουμε τη θεωρία
του αντίστροφου σκεδασμού Compton και θα δώσουμε μερικές αστροφυσικές
εφαρμογές.
΄Οπως είναι γνωστό από τον Ηλεκτρομαγνητισμό τα φορτία που επιταχύνονται ακτινοβολούν. Αυτή η αρχή είναι η βάση της θεωρίας των διαφόρων ακτινοβολιών. Η ισχύς της ακτινοβολίας που παράγεται δίνεται από τη σχέση του Larmor
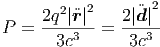 | (5.1) |
όπου q το φορτίο, |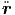 | το μέτρο της επιτάχυνσής του στο στιγμιαίο σύστημα ηρεμίας
του φορτίου και c η ταχύτητα του φωτός. Η παραπάνω σχέση εκφράζεται ακόμη και
ως συνάρτηση της διπολικής ροπής d = qr.
| το μέτρο της επιτάχυνσής του στο στιγμιαίο σύστημα ηρεμίας
του φορτίου και c η ταχύτητα του φωτός. Η παραπάνω σχέση εκφράζεται ακόμη και
ως συνάρτηση της διπολικής ροπής d = qr.
Η γωνιακή κατανομή της ακτινοβολίας ακολουθεί την κατανομή δίπολου και
δίνεται από τη σχέση
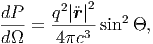 | (5.2) |
όπου Θ η γωνία μεταξύ της διεύθυνσης της επιτάχυνσης και της διεύθυνσης της
εκπεμπόμενης ακτινοβολίας. ΄Οπως παρατηρούμε δεν εκπέμπεται καθόλου ακτινοβολία
κατά τη διεύθυνση της επιτάχυνσης, ενώ η μεγίστη εκπομπή επιτυγχάνεται κάθετα
σε αυτήν τη διεύθυνση [σχήμα 5.1].
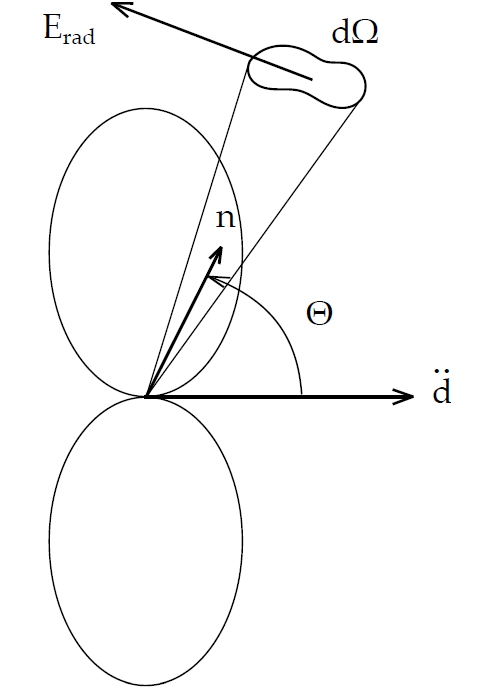
Σημείωση: Η σχέση (5.1) προκύπτει κατευθείαν από την (5.2), εάν ολοκληρώσουμε αυτήν την τελευταία ως προς στερεά γωνία, δηλαδή
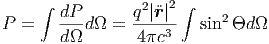 |
Στην περίπτωση τώρα που ένα γραμμικά πολωμένο ηλεκτρομαγνητικό κύμα χαμηλής συχνότητας ω0 προσπίπτει σε ένα ηλεκτρόνιο σε ηρεμία η δύναμη που του ασκεί είναι:
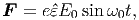 | (5.3) |
όπου e το φορτίο και 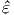 το μοναδιαίο διάνυσμα κατά τη διεύθυνση της έντασης του
ηλεκτρικού πεδίου E. Από τις (5.1) και (5.3), χρησιμοποιώντας επιπλέον τις σχέσεις
F = m
το μοναδιαίο διάνυσμα κατά τη διεύθυνση της έντασης του
ηλεκτρικού πεδίου E. Από τις (5.1) και (5.3), χρησιμοποιώντας επιπλέον τις σχέσεις
F = m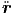 και < sin 2ω
0t >=
και < sin 2ω
0t >= 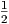 , παίρνουμε
, παίρνουμε
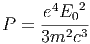 | (5.4) |
ενώ η (5.2) δίνει αντίστοιχα
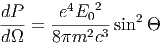 | (5.5) |
Ορίζουμε στη συνέχεια τη διαφορική ενεργό διατομή ως
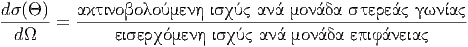 |
Η εισερχόμενη ισχύς ανά μονάδα επιφανείας δεν είναι άλλη από τη ροή Poynting που δίνεται από < S >= (c∕8π)E02. Συνεπώς από τον παραπάνω ορισμό της διαφορικής ενεργού διατομής έχουμε
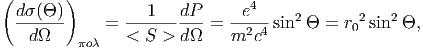 | (5.6) |
όπου η ποσότητα
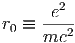 | (5.7) |
είναι η κλασική ακτίνα του ηλεκτρονίου και δίνει ένα μέτρο της «ακτίνας» του φορτίου του. Η τιμή της είναι r0 = 2.82 × 10-13 cm. Η ολική ενεργός διατομή βρίσκεται από την (5.6) με ολοκλήρωση ως προς τη στερεά γωνία και ισούται με
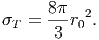 | (5.8) |
Η ποσότητα σT ονομάζεται ενεργός διατομή Thomson και ισούται με
0.665 × 10-24cm2, ενώ η φυσική διαδικασία που μόλις περιγράψαμε ονομάζεται
σκεδασμός Thomson ή σκεδασμός ηλεκτρονίου . Αξίζει να σημειώσουμε ότι
οι σχέσεις (5.6) και (5.8) που δίνουν τη διαφορική και την ολική ενεργό
διατομή είναι ανεξάρτητες της συχνότητας του προσπίπτοντος κύματος.
Ωστόσο αυτό ισχύει για πολύ χαμηλές συχνότητες ώστε να μπορούμε να
χρησιμοποιήσουμε την κλασική προσέγγιση. ΄Οπως θα δούμε στην παράγραφο
5.2, για υψηλές συχνότητες η ενεργός διατομή προσδιορίζεται πλέον από
την Κβαντομηχανική και εξαρτάται από τη συχνότητα του προσπίπτοντος
φωτονίου.
Ο σκεδασμός που εξετάσαμε αφορούσε πολωμένη ακτινοβολία. Είναι εύκολο τα
αποτελέσματα που βρήκαμε να επεκταθούν και στη γενικότερη περίπτωση της μη
πολωμένης ακτινοβολίας εάν θυμηθούμε ότι αυτή μπορεί να θεωρηθεί ως
μία επαλληλία δύο γραμμικά πολωμένων κυμάτων που ταλαντώνονται σε
ορθογώνια επίπεδα. Συνεπώς αναλύουμε το ηλεκτρικό πεδίο της προσπίπτουσας
δέσμης σε δύο συνιστώσες από τις οποίες η μία (με μοναδιαίο διάνυσμα
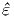 1) βρίσκεται στο επίπεδο που ορίζουν η διεύθυνση της ακτινοβολίας πριν
και μετά τον σκεδασμό (όπως αυτές ορίζονται από τα διανύσματα
1) βρίσκεται στο επίπεδο που ορίζουν η διεύθυνση της ακτινοβολίας πριν
και μετά τον σκεδασμό (όπως αυτές ορίζονται από τα διανύσματα 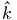 και
και 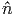 αντίστοιχα σχήμα 5.3), ενώ η άλλη (με μοναδιαίο διάνυσμα
αντίστοιχα σχήμα 5.3), ενώ η άλλη (με μοναδιαίο διάνυσμα 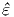 2) είναι κάθετη σε
αυτό το επίπεδο. ΄Εστω Θ η γωνία μεταξύ των
2) είναι κάθετη σε
αυτό το επίπεδο. ΄Εστω Θ η γωνία μεταξύ των 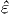 1 και
1 και 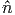 . Ορίζουμε επίσης
τη γωνία θ, που είναι η γωνία μεταξύ της διεύθυνσης της σκεδασμένης
και προσπίπτουσας δέσμης: θ = π∕2 - Θ. Η διαφορική ενεργός διατομή
της μη πολωμένης ακτινοβολίας είναι η μέση τιμή των ενεργών διατομών
των δύο παραπάνω συνιστωσών που είναι γραμμικά πολωμένες. Γράφουμε
λοιπόν:
. Ορίζουμε επίσης
τη γωνία θ, που είναι η γωνία μεταξύ της διεύθυνσης της σκεδασμένης
και προσπίπτουσας δέσμης: θ = π∕2 - Θ. Η διαφορική ενεργός διατομή
της μη πολωμένης ακτινοβολίας είναι η μέση τιμή των ενεργών διατομών
των δύο παραπάνω συνιστωσών που είναι γραμμικά πολωμένες. Γράφουμε
λοιπόν:
![( ) [( ) ( ) ]
dσ(Θ-) = 1- dσ-(Θ) + dσ-(π∕2) = 1r02(1+sin2 Θ ) = 1r02(1+cos2 θ).
dΩ 2 dΩ πoλ dΩ πoλ 2 2](HEA_files/HEA70x.png) | (5.9) |
Παρατηρούμε ότι το αποτέλεσμα εξαρτάται μόνο από τη διεύθυνση της προσπίπτουσας και σκεδασμένης ακτινοβολίας.
Δύο βασικές ιδιότητες του σκεδασμού της μη πολωμένης ακτινοβολίας
είναι:
1. Είναι συμμετρικός ως προς τον μετασχηματισμό θ →-θ (μπρος-πίσω).
2. Η ολική ενεργός διατομή είναι ίση με σT , ίση δηλαδή με την περίπτωση της
πολωμένης ακτινοβολίας.
Οι σχέσεις (5.8) και (5.9) αποτελούν τα βασικά αποτελέσματα του σκεδασμού
Thomson, όπου το φωτόνιο προσεγγίζεται με ένα συνεχές ηλεκτρομαγνητικό κύμα.
Αυτή η προσέγγιση ισχύει όταν η ενέργεια της προσπίπτουσας ακτινοβολίας
είναι πολύ μικρότερη της ενέργειας ηρεμίας του ηλεκτρονίου, όταν δηλαδή
ϵ = hν << mec2. ΄Ενα ακόμα βασικό αποτέλεσμα είναι ότι ο σκεδασμός είναι
ελαστικός, ισχύει δηλαδή ϵ = ϵ1, όπου ϵ και ϵ1 η ενέργεια του φωτονίου πριν και
μετά τον σκεδασμό αντίστοιχα.
Κβαντικά φαινόμενα υπεισέρχονται στην παραπάνω εικόνα με δύο τρόπους.
Πρώτον, όσο αυξάνεται η ενέργεια του φωτονίου ο σκεδασμός παύει να είναι
ελαστικός (δηλαδή ϵ≠ϵ1), καθώς το ηλεκτρόνιο αρχίζει να παίρνει ένα διαρκώς
αυξανόμενο μέρος της ορμής και της ενέργειας του προσπίπτοντος φωτονίου. Επίσης
ο υπολογισμός της ενεργού διατομής της αλληλεπίδρασης ξεφεύγει πλέον από τα
όρια του Ηλεκτρομαγνητισμού και γίνεται αντικείμενο της Κβαντοηλεκτροδυναμικής.
Συνοψίζοντας:
1. ΄Οριο Thomson: Στο μη σχετικιστικό όριο (x = ϵ∕mec2 << 1) η ενεργός διατομή
δίνεται από σ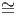 σT σύμφωνα με τα όσα είπαμε προηγουμένως.
σT σύμφωνα με τα όσα είπαμε προηγουμένως.
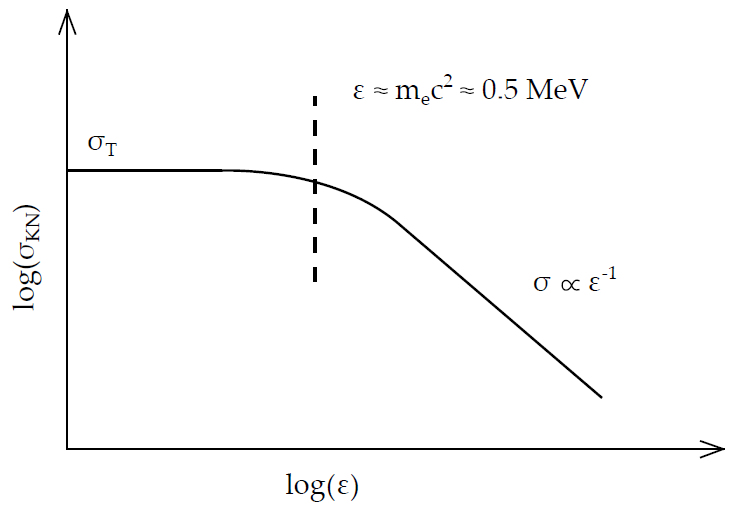
2. ΄Οριο Klein Nishina: Στο σχετικιστικό όριο (x = ϵ∕mec2 >> 1) η ενεργός
διατομή δίνεται από τη σχέση
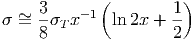 | (5.10) |
δηλαδή η ενεργός διατομή ελαττώνεται όσο αυξάνεται η ενέργεια του φωτονίου.
Ας θεωρήσουμε ένα σχετικιστικό ηλεκτρόνιο κινούμενο μέσα σε πεδίο μονοχρωματικών
ισοτροπικών φωτονίων κατά τη διεύθυνση του άξονα των x στο σύστημα ηρεμίας του
παρατηρητή Κ. ΄Εστω θ η γωνία ανάμεσα στις διευθύνσεις ηλεκτρονίου-εισερχόμενου
φωτονίου1 .
Στο σύστημα ηρεμίας του ηλεκτρονίου Κ΄ οι αντίστοιχες γωνίες θ′ δίνονται από τις
γνωστές σχέσεις αποπλάνησης του φωτός
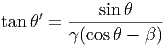 | (5.11) |
και
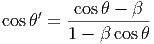 | (5.12) |
όπου γ και βc είναι αντιστοίχως ο παράγοντας Lorentz και η ταχύτητα του ηλεκτρονίου στο σύστημα ηρεμίας του παρατηρητή. ΄Οταν γ »1, τότε όλα τα φωτόνια (εκτός αυτών που κινούνται κατά μήκος του άξονα x, δηλαδή παράλληλα με τη διεύθυνση του ηλεκτρονίου) εμφανίζονται από τη διεύθυνση θ ≈ π.
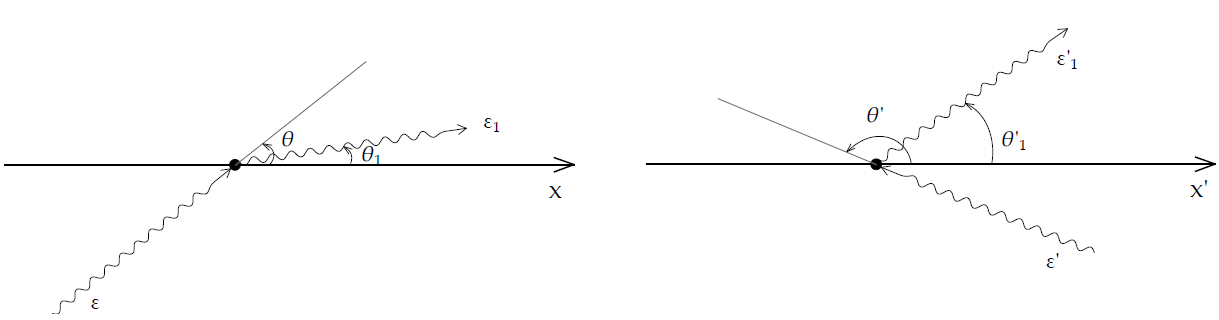
Η ενέργεια των φωτονίων στο Κ΄ δίνεται από τη γνωστή σχέση του Doppler
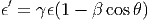 | (5.13) |
και κατά συνέπεια παίρνει τιμές από ϵmin′ ≈ ϵ∕2γ, για θ = 0 έως ϵ max′ ≈ 2ϵγ για θ = π. Παρατηρούμε ότι τα φωτόνια εμφανίζονται με πολύ χαμηλές ενέργειες όταν κατευθύνονται σχεδόν παράλληλα με το ηλεκτρόνιο, ενώ αντίθετα εμφανίζονται πολύ πιο ενεργητικά όταν οι συγκρούσεις είναι μετωπικές. Εάν ως μέση τιμή της ενέργειας του φωτονίου πάρουμε την < ϵ′ >= γϵ, τότε έχουμε ότι όταν
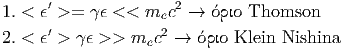 | (5.14) |
Παρόλο που θα μπορούσαμε να υπολογίσουμε τα διάφορα ζητούμενα μεγέθη στο σύστημα ηρεμίας του ηλεκτρονίου και στη συνέχεια να μετασχηματίσουμε στο σύστημα ηρεμίας του παρατηρητή, είναι καλύτερο να χρησιμοποιήσουμε τετρανύσματα. ΄Εστω λοιπόν P και K τα τετρανύσματα της ορμής του ηλεκτρονίου και του φωτονίου πριν τον σκεδασμό και P 1και K 1 τα αντίστοιχα τετρανύσματα μετά τον σκεδασμό. Δηλαδή:
| Ηλεκτρόνιο P = [γmec,γmev] P1 = [γ1mec,γ1mev1] | ||
Φωτόνιο K = ![[ ]
h ν h ν
---,---^ek
c c](HEA_files/HEA77x.png) K1 = K1 = ![[ ]
hν1 hν1
---, ---^ek1
c c](HEA_files/HEA78x.png) | ||
| Πριν τον σκεδασμό Μετά τον σκεδασμό |
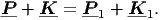 | (5.15) |
ϒψώνουμε στη συνέχεια στο τετράγωνο και χρησιμοποιούμε τις σχέσεις P⋅P = P 1 ⋅P 1 = -me2c2 και K ⋅K = K 1 ⋅K 1 = 0. Συνεπώς είναι εύκολο να δειχτεί (άσκηση!) ότι
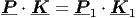 | (5.16) |
Πολλαπλασιάζουμε τώρα τα μέλη της (5.15) με K 1 και με τη βοήθειά της (5.16) καταλήγουμε στη σχέση
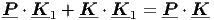 | (5.17) |
η οποία είναι και η ζητούμενη. Χρησιμοποιούμε στη συνέχεια τον ορισμό του
εσωτερικού γινομένου δύο τετρανυσμάτων και ορίζουμε τις γωνίες οι οποίες
υπεισέρχονται στον σκεδασμό ως [βλ. και σχήμα 5.5]:
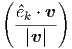
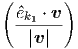
Από την (5.17) βρίσκουμε:
![ϵ 1 - (v∕c)cosθ
-1 = ---------------------------------------
ϵ [1 - (v∕c)cos θ1 + (ϵ∕γmec2 )(1 - cosα )]](HEA_files/HEA84x.png) | (5.18) |
Η παραπάνω σχέση είναι σημαντική για τον σκεδασμό Compton (τόσο τον ευθύ όσο και τον αντίστροφο) και αξίζει να σταθούμε για λίγο σε αυτήν. Καταρχήν, όταν το ηλεκτρόνιο είναι σε ηρεμία (v = 0, γ = 1), αυτή περιγράφει το γνωστό φαινόμενο Compton:
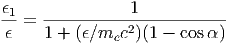 | (5.19) |
η οποία εκφράζεται ακόμα ως συνάρτηση του μήκους κύματος του φωτονίου
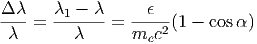 | (5.20) |
Επίσης η σχέση (5.18) μας επιτρέπει να υπολογίσουμε τη μέγιστη ενέργεια
που μπορεί να αποκτήσει ένα φωτόνιο όταν σκεδάζεται με ένα σχετικιστικό
ηλεκτρόνιο.
Πράγματι στο όριο Thomson όπου ϵ << γmec2 το δεξί μέλος της (5.18) γίνεται
μέγιστο όταν θ=π και θ1 = 0 (όταν έχουμε δηλαδή μετωπική σύγκρουση
ηλεκτρονίου-φωτονίου και το φωτόνιο μετά τον σκεδασμό κινείται παράλληλα με το
ηλεκτρόνιο: αν και η πρώτη συνθήκη αποδεικνύεται πολύ πιο ισχυρή από τη δεύτερη).
Σε αυτήν την περίπτωση είναι εύκολο να δειχτεί ότι:
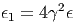 | (5.21) |
που είναι και η ζητούμενη μέγιστη ενέργεια.
Σημείωση: Αξίζει να αναπαράγουμε την παραπάνω σχέση χρησιμοποιώντας απλούς μετασχηματισμούς ανάμεσα σε συστήματα αναφοράς. ΄Εστω λοιπόν ότι μετά από έναν σκεδασμό (όπως αυτός μετράται στο Κ΄) το φωτόνιο αποκτά ενέργεια ϵ1′ ενώ σχηματίζει γωνία α΄ με τη διεύθυνση του φωτονίου πριν τον σκεδασμό. Προφανώς ισχύει η σχέση (5.19), η οποία γράφεται·
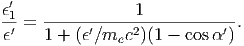 |
Επειδή έχουμε θεωρήσει σκεδασμό στο όριο Thomson ισχύει ϵ′ << mec2 και συνεπώς ϵ1′ = ϵ′ (δηλαδή τα γνωστά περί ελαστικού σκεδασμού στο όριο Thomson). Ισχύει όμως η σχέση (5.13) καθώς και η σχέση:
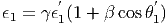 |
Παίρνοντας, όπως προηγουμένως, την περίπτωση όπου θ = π και θ1 = 0, βρίσκουμε αμέσως τη ζητούμενη (5.21).
Μία παρουσίαση των ενεργειακών απωλειών για τα σχετικιστικά ηλεκτρόνια στο όριο Thomson (βλ. σχέση 5.14) δίνει ο Longair. Οι ενεργειακές απώλειες στο σύστημα ηρεμίας του ηλεκτρονίου Κ΄ δίνονται από τη σχέση
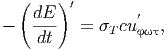 | (5.22) |
όπου uφωτ είναι η ενεργειακή πυκνότητα των φωτονίων.
Επειδή η ενέργεια και ο χρόνος μετασχηματίζονται με τον ίδιο τρόπο, ισχύει δηλαδή
dE = γdE′ και dt = γdt′, έχουμε
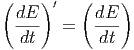 | (5.23) |
συνεπώς για να υπολογίσουμε τις ενεργειακές απώλειες του ηλεκτρονίου αρκεί να
υπολογίσουμε την ενεργειακή πυκνότητα των φωτονίων όπως αυτή μετράται
στο σύστημα ηρεμίας του ηλεκτρονίου Κ΄ (η ενεργειακή πυκνότητα των
φωτονίων uφωτ στο σύστημα ηρεμίας του παρατηρητή Κ θεωρείται γνωστή).
Για να υπολογίσουμε την ενεργειακή πυκνότητα των φωτονίων στο Κ΄
χρειαζόμαστε δύο ποσότητες: την ενέργεια κάθε φωτονίου στο Κ΄ και τον ρυθμό με
τον οποίο φτάνουν αυτά στο ηλεκτρόνιο. Το πρώτο ζητούμενο, δηλαδή η
ενέργεια, δίνεται από τη σχέση (5.13). Για να βρούμε τη μετρούμενη ροή
εργαζόμαστε ως εξής: ΄Εστω θ η γωνία υπό την οποία η δέσμη φωτονίων
προσπίπτει στο Κ. Αυτή συνδέεται με την αντίστοιχη γωνία θ΄ την οποία
μετράει παρατηρητής στο σύστημα Κ΄ σύμφωνα με τις σχέσεις (5.11) και
(5.12). Ας θεωρήσουμε τώρα δύο φωτόνια τα οποία φτάνουν στο Κ΄ τις
χρονικές στιγμές t1′ και t2′. Οι συντεταγμένες των γεγονότων αυτών στο Κ
είναι
![′ ′ ′ ′
[x1, 0,0,t1] = [γvt1,0,0,γt1] και [x2,0,0,t2] = [γvt2,0, 0,γt2]](HEA_files/HEA92x.png) |
αντίστοιχα. Ο υπολογισμός αυτός κάνει την υπόθεση ότι τα φωτόνια της δέσμης κινούνται σε παράλληλες τροχιές, όπως δείχνει και το σχήμα 5.6. Από το ίδιο σχήμα φαίνεται επίσης ότι η χρονική διαφορά με την οποία τα φωτόνια φτάνουν σε ένα επίπεδο κάθετο προς τη διεύθυνση διάδοσής τους είναι
![(x - x ) [ v ]
Δt = t2 - --2----1-cos θ - t1 = (t′2 - t′1)γ 1 - --cosθ ,
c c](HEA_files/HEA93x.png) | (5.24) |
με άλλα λόγια η χρονική διαφορά είναι μικρότερη κατά έναν παράγοντα γ(1 -β cos θ)
στο Κ΄ απο ότι στο Κ. Παρατηρούμε ότι αυτός ο παράγοντας είναι ακριβώς ο ίδιος με
αυτόν που υπεισέρχεται στη σχέση του Doppler (5.13).
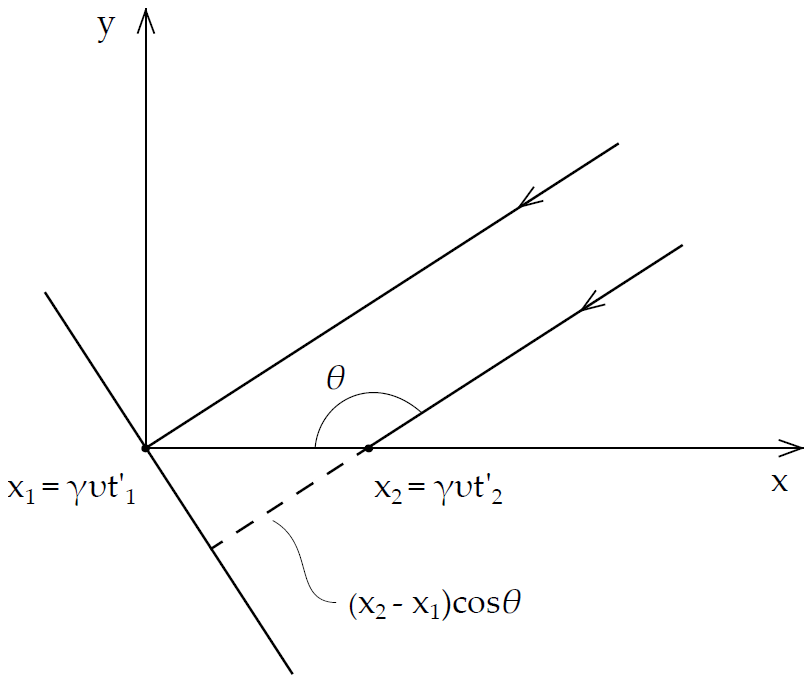
Συνεπώς η ενεργειακή πυκνότητα της δέσμης φωτονίων που προσπίπτουν με γωνία θ στο σύστημα Κ είναι
![u ′ (θ) = [γ(1 - β cosθ)]2u
φω τ φωτ](HEA_files/HEA94x.png) | (5.25) |
ϒπολογίζουμε στη συνέχεια την ολική ενεργειακή πυκνότητα ολοκληρώνοντας ως προς τη στερεά γωνία, οπότε
![′ ∫ π 2 1
uφωτ = uφωτ 0 [γ(1 - β cosθ) ]2-sin θdθ](HEA_files/HEA95x.png) | (5.26) |
και συνεπώς
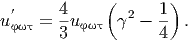 | (5.27) |
Χρησιμοποιώντας τις σχέσεις (5.22) και (5.23) βρίσκουμε
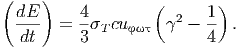 | (5.28) |
Αυτή είναι η ενέργεια που κερδίζουν τα φωτόνια εξ αιτίας των σκεδασμών.
Ταυτόχρονα όμως αυτά χάνουν την ενέργεια αυτών που σκεδάζονται και που ισούται
με σT cuφωτ. Τελικά έχουμε λοιπόν
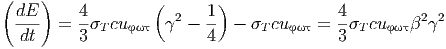 | (5.29) |
που δίνει τις συνολικές ενεργειακές απώλειες ηλεκτρονίων ενέργειας Ee = γmec2 όταν αυτά βρίσκονται σε ισοτροπικό πεδίο φωτονίων ενεργειακής πυκνότητας uφωτ, υπό την προϋπόθεση ότι οι σκεδασμοί ηλεκτρονίων-φωτονίων πραγματοποιούνται στο όριο Thomson (σχέση 5.6).
Σημείωση: Μία άλλη, πιο αυστηρή, απόδειξη της σχέσης (5.27) προκύπτει από τις εξισώσεις διάδοσης ακτινοβολίας. Ξεκινάμε από το βασικό αποτέλεσμα, ότι το πηλίκο Iν∕ν3 παραμένει αναλλοίωτο σε μετασχηματισμούς Lorentz, όπου η ποσότητα Iν είναι η ειδική ένταση ακτινοβολίας (για τους ορισμούς βλ. κεφάλαιο 3.1.1). Συνεπώς ανάμεσα στα συστήματα Κ και Κ΄ ισχύει η σχέση
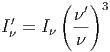 | (5.30) |
Επίσης είναι γνωστό από τη θεωρία διάδοσης της ακτινοβολίας ότι η ειδική ενεργειακή πυκνότητα (δηλαδή η ενεργειακή πυκνότητα ανά συχνότητα ανά στερεά γωνία) δίνεται από τη σχέση:
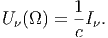 | (5.31) |
Συνεπώς ορίζοντας
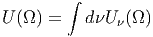 |
και χρησιμοποιώντας τις σχέσεις (5.13), (5.30) και (5.31) μπορούμε να συσχετίσουμε τη διαφορική ενεργειακή πυκνότητα στα συστήματα Κ και Κ΄
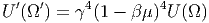 | (5.32) |
Ορίζουμε στη συνέχεια την ολική ενεργειακή πυκνότητα των φωτονίων ως uφωτ ≡ ∫ dΩU(Ω) και χρησιμοποιούμε ότι το διαφορικό της στερεάς γωνίας μετασχηματίζεται σύμφωνα με τη σχέση
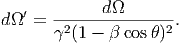 | (5.33) |
Το επόμενο ζητούμενο είναι ο προσδιορισμός του φάσματος της ακτινοβολίας που σκεδάζεται στο όριο Thomson. Μία ανάλυση υπάρχει στο άρθρο των Blumenthal & Gould, εδώ απλώς επαναλαμβάνουμε το αποτέλεσμα για λόγους πληρότητας. ΄Εστω ότι ηλεκτρόνιο ενέργειας Ee = γmec2 εισέρχεται σε ισοτροπικό πεδίο φωτονίων ενέργειας ϵ και έστω ϵ1 η ενέργεια των σκεδαζόμενων φωτονίων. Ο ολοκληρωμένος ως προς στερεά γωνία συντελεστής εκπομπής (διαστάσεις [jν]= (ακτινοβολούμενη) ενέργεια/χρόνος/ ενέργεια εκπομπής) δίνεται από τη σχέση
![[ ( ) ]
∫ 3σTc n(ϵ) ϵ1 2 ϵ12
jics(ϵ1) = ---4---2-ϵ1 2ϵ1ln ---2- + ϵ1 + 4γ ϵ - --2-- dϵ.
16γ ϵ 4 γ ϵ 2γ ϵ](HEA_files/HEA104x.png) | (5.34) |
Τη μορφή της ολοκληρωτέας ποσότητας δίνει το σχήμα 5.7. Η ποσότητα n(ϵ) είναι η διαφορική αριθμητική πυκνότητα των φωτονίων του πεδίου (διαστάσεις [n(ϵ)]= φωτόνια/όγκος/ενέργεια) και ορίζεται ως ∫ 0∞n(ϵ)dϵ = n ϕωτ, όπου nϕωτ η ολική αριθμητική πυκνότητα των φωτονίων.
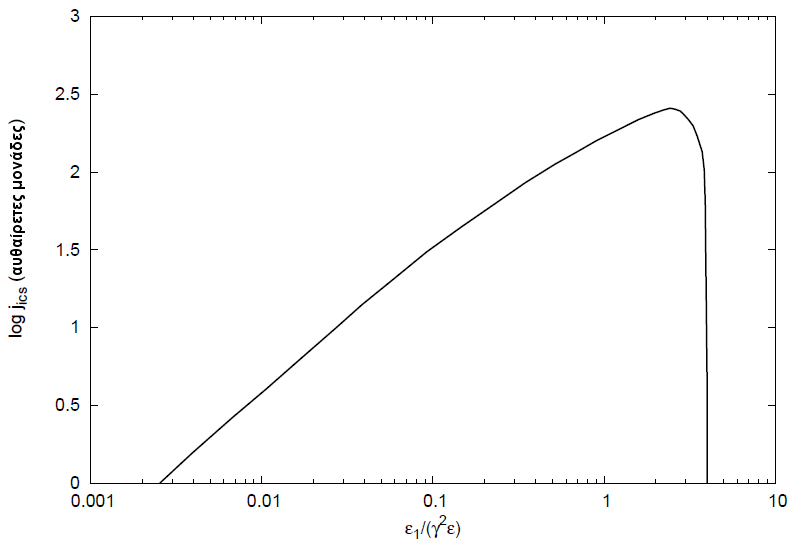
Από το σχήμα 5.7 παρατηρούμε ότι το φάσμα εκτείνεται μέχρι την ενέργεια ϵ1max = 4γ2ϵ, σε συμφωνία με τη σχέση (5.21), και ότι παρουσιάζει μέγιστο κοντά σε αυτή την ενέργεια. Προφανώς το συνολικό φάσμα βρίσκεται μετά από ολοκλήρως·η της (5.34) ως προς όλες τις ενέργειες των χαμηλοενεργειακών φωτονίων τα οποία έχουν κατανομή n(ϵ). Για να απλουστεύσουμε το πρόβλημα ας θεωρήσουμε ότι το πεδίο φωτονίων είναι μονοχρωματικό, ισχύει δηλαδή n(ϵ) = n0δ(ϵ - ϵ0). Τότε από την (5.34) μπορούμε να υπολογίσουμε τη μέση ενέργεια των φωτονίων μετά τον σκεδασμό τους. Βρίσκουμε
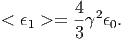 | (5.35) |
Σημείωση: Στο ίδιο αποτέλεσμα καταλήγουμε και με έναν πιο εμπειρικό τρόπο. Θεωρούμε ότι σε κάθε σκεδασμό το ποσό ενέργειας που χάνει ένα ηλεκτρόνιο ισούται με την ενέργεια του φωτονίου μετά τον σκεδασμό του. Ισχύει λοιπόν η σχέση Ενεργειακές απώλειες = (Μέση ενέργεια φωτονίου) × (Ρυθμός σκεδασμών). Ο ρυθμός σκεδασμών δίνεται από τη σχέση
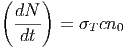 | (5.36) |
ενώ οι ενεργειακές απώλειες δίνονται από τη σχέση (5.29). Χρησιμοποιώντας επιπλέον τη σχέση
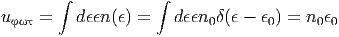 | (5.37) |
βρίσκουμε ότι
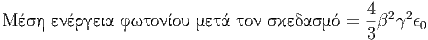 |
η οποία για γ>>1 (οπότε β ≈ 1) γίνεται η σχέση (5.35). Η σημασία του αντίστροφου σκεδασμού Compton για την Αστροφυσική ϒψηλών Ενεργειών γίνεται τώρα προφανής. Ηλεκτρόνια με παράγοντα Lorentz γ σκεδάζουν φωτόνια χαμηλών ενεργειών σε ενέργειες που είναι υψηλότερες κατά έναν παράγοντα γ2. Για παράδειγμα, ηλεκτρόνια με γ=1000 σκεδάζουν ραδιοφωτόνια στο υπεριώδες, υπέρυθρα φωτόνια στις ακτίνες Χ και οπτικά φωτόνια στις ακτίνες γ.
Στις περισότερες περιπτώσεις με αστροφυσικό ενδιαφέρον τα ηλεκτρόνια δεν έχουν μονοενεργητική κατανομή αλλά κατανομή που είναι νόμος δύναμης, δηλαδή Ne(E) ∝ E-p ∝ (γm ec2)-p ∝ γ-p, οπότε έχουμε:
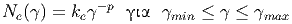 | (5.38) |
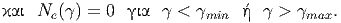 |
Τα όρια της κατανομής των ηλεκτρονίων δεν είναι γνωστά αλλά εξαρτώνται από
τον μηχανισμό επιτάχυνσης που δρα στη συγκεκριμένη περίπτωση. Εδώ θα τα
θεωρήσουμε ως ελεύθερες παραμέτρους.
Το φάσμα των σκεδασμένων φωτονίων που παράγεται σε αυτήν την περίπτωση
βρίσκεται αν ολοκληρώσουμε το φάσμα (5.34), το οποίο παράγεται από
μονοενεργητικά ηλεκτρόνια, ως προς όλες τις ενέργειες των ηλεκτρονίων. ΄Εχουμε
λοιπόν:
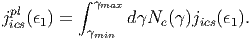 | (5.39) |
Το παραπάνω ολοκλήρωμα υπολογίζεται αναλυτικά (βλ. π.χ. το άρθρο των
Blumenthal και Gould). Ωστόσο είναι πιο απλό να εκμεταλλευτούμε το γεγονός ότι
η συνάρτηση jics(ϵ1) παρουσιάζει ένα μέγιστο κοντά στην ενέργεια ϵ1* = 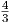 γ2ϵ
0 και
να θέσουμε
γ2ϵ
0 και
να θέσουμε
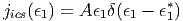 | (5.40) |
προσεγγίζουμε δηλαδή, όπως υποδηλώνει η συνάρτηση δέλτα, το φάσμα του
σχήματος 5.7 με μονοενεργητική εκπομπή στη μέση ενέργεια σκεδασμού. Η σταθερά
A υπολογίζεται από την απαίτησή μας ο ρυθμός της ακτινοβολούμενης ενέργειας των
φωτονίων να ισούται με τον ρυθμό απώλειας ενέργειας του ηλεκτρονίου (σχέση
5.29). Εξισώνοντας βρίσκουμε A = n0σT c.
Αντικαθιστώντας την (5.40) στην (5.39) βρίσκουμε
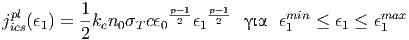 | (5.41) |
όπου
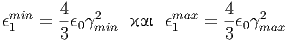 | (5.42) |
Παρατηρούμε ότι η εκπομπή είναι νόμος δύναμης με εκθέτη ο οποίος καθορίζεται από την κατανομή των ηλεκτρονίων. ΄Εχουμε δηλαδή ότι το παραγόμενο φάσμα (και κατά συνέπεια η ροή – βλ. κεφάλαιο 3.1.1) των φωτονίων είναι της μορφής Fν ∝ Iν ∝ ν-α με
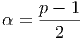 | (5.43) |
Η διαφορά στους εκθέτες ηλεκτρονίων και φωτονίων οφείλεται στο ότι η μέση ενέργεια των φωτονίων μετά τη σκέδαση συνδέεται με το τετράγωνο της ενέργειας του ηλεκτρονίου. Η παραπάνω σχέση είναι σημαντική γιατί μας επιτρέπει να εξάγουμε από παρατηρησιακά δεδομένα την ενεργειακή κατανομή των ηλεκτρονίων, συνεπώς μας δίνει πληροφορίες για τις φυσικές συνθήκες στην πηγή των φωτονίων. Πράγματι σε πολλές περιπτώσεις έχουμε μετρήσεις για τις παραμέτρους n0 και ϵ0 του πεδίου φωτονίων καθώς και το φάσμα της πηγής στις υψηλές ενέργειες. Με βάση αυτά τα στοιχεία μπορούμε να υπολογίσουμε τα χαρακτηριστικά των ηλεκτρονίων υψηλών ενεργειών που υπάρχουν σε αυτές.
Ο ανιχνευτής Fermi ανακάλυψε περίπου 1000 ενεργούς γαλαξίες (που όλοι ανήκουν στην κατηγορία των blazars) να εκπέμπουν στις σκληρές ακτίνες γ. Αυτή η ανακάλυψη φανέρωσε για πρώτη φορά ότι οι ενεργοί γαλαξίες επιταχύνουν σωματίδια σε υψηλές ενέργειες. Μία σχεδόν καθολικά αποδεκτή θεωρία για τους blazars προτείνει ότι πρόκειται περί ενεργών γαλαξιών με τους πίδακές τους στραμμένους προς την κατεύθυνση της Γης (σε αντίθεση με τους ραδιογαλαξίες που έχουν τους πίδακες σε μεγάλες γωνίες ως προς την κατεύθυνση της Γης). Αυτός ο χαρακτηριστικός προσανατολισμός είναι που προσδίδει στους blazars τις ιδιομορφίες τους (ταχύτατες αυξομειώσεις στην ένταση, ισχυρή πόλωση, σε πολλές περιπτώσεις υπέρφωτη κίνηση και ακτινοβολία γ) μιας και η συνολική εκπομπή τους κυριαρχείται από την εκπομπή του πίδακά τους.
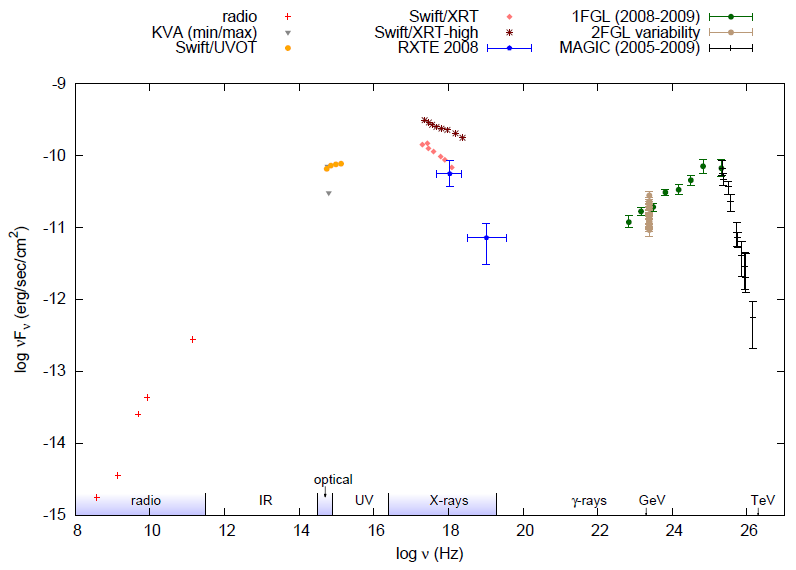
Το σχήμα 5.8 παρουσιάζει το φάσμα εκπομπής από τον blazar PG 1553+113. Το
εύρος του καλύπτει από τα ραδιοκύματα (1 GHz) έως ενέργειες γ πολύ
υψηλών ενεργειών (10 TeV). Αυτό που προκαλεί εντύπωση δεν είναι μόνο οι
19 τάξεις μεγέθους που καλύπτει η εκπομπή του συγκεκριμένου blazar,
αλλά και η συνεχής μεταβολή της ροής που παρατηρείται κυρίως σε ακτίνες
Χ και γ. ΄Οπως και στην περίπτωση των pulsars, μία από τις βασικές
απόψεις για την ακτινοβολία γ (ενέργειες από 1 MeV έως 10 TeV) είναι ότι
πρόκειται για αντίστροφο σκεδασμό Compton σχετικιστικών ηλεκτρονίων.
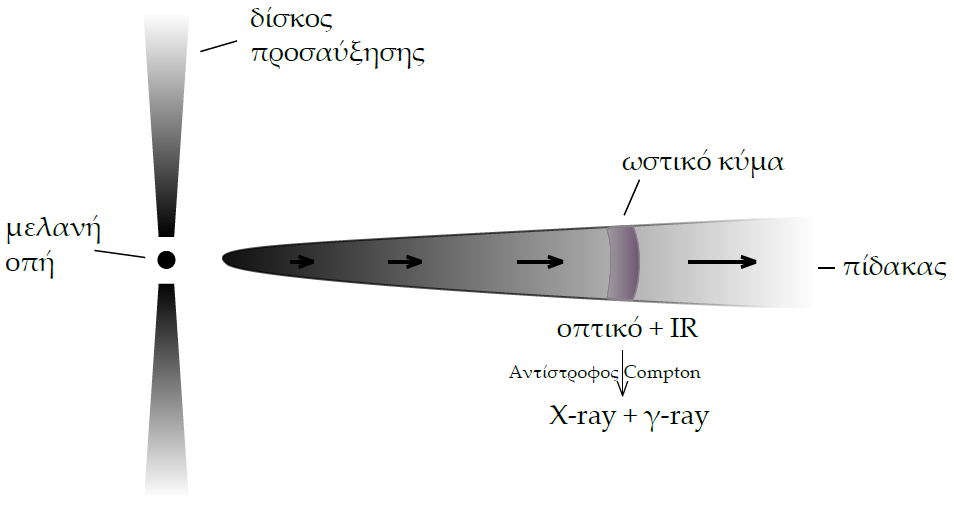
Τα ηλεκτρόνια επιταχύνονται σε ωστικά κύματα που οδεύουν στους
πίδακες2
και σκεδάζουν σε υψηλές ενέργειες είτε φωτόνια του δίσκου προσαύξησης της
κεντρικής μελανής οπής είτε φωτόνια των γραμμών εκπομπής [σχήμα 5.9]. Επειδή τα
φωτόνια αυτά έχουν ενέργειες από υπέρυθρο έως το υπεριώδες μέρος του φάσματος
(ϵ0 ≈ 0.1eV ) και οι ακτίνες γ μπορούν να φτάσουν τουλάχιστον μέχρι 1 TeV,
βρίσκουμε ότι απαιτούνται ηλεκτρόνια με παράγοντες Lorentz γ ≈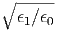 = 3 ⋅ 107.
= 3 ⋅ 107.
΄Οπως ήδη έχουμε αναφέρει, σε περιπτώσεις όπου ο παράγοντας Lorentz των
ηλεκτρονίων και η ενέργεια ε των φωτονίων πριν τη σκέδαση ικανοποιούν τη σχέση
γϵ >> mec2 δεν μπορούμε πλέον να χρησιμοποιήσουμε την κλασική προσέγγιση για
να περιγράψουμε την αλληλεπίδραση. Αντίθετα θα πρέπει να θεωρήσουμε το φωτόνιο
ως σωμάτιο και να χρησιμοποιήσουμε την κβαντική εκδοχή της ενεργού διατομής του
σκεδασμού που δίνεται από τη σχέση (5.10). Επειδή αυτή ελαττώνεται όσο αυξάνει η
ενέργεια της σύγκρουσης, ελαττώνεται και ο ρυθμός των συγκρούσεων
ηλεκτρονίων-φωτονίων. Ταυτόχρονα μπορεί να δειχθεί, με ανάλογη μέθοδο με αυτή
που οδήγησε στη σχέση (5.21), ότι η μέση τιμή της ενέργειας που λαμβάνει ένα
φωτόνιο μετά τον σκεδασμό αυξάνεται και ότι για πολύ υψηλές τιμές του
γινομένου γϵ αυτή μπορεί να πλησιάσει την ενέργεια του ηλεκτρονίου. Στο
ακραίο δηλαδή σχετικιστικό όριο του αντίστροφου σκεδασμού Compton
έχουμε μεν πιο αραιές συγκρούσεις ηλεκτρονίων-φωτονίων αλλά σε αυτές
τις συγκρούσεις τα ηλεκτρόνια δίνουν όλη τους σχεδόν την ενέργεια στα
φωτόνια σκεδάζοντάς τα σε πολύ υψηλές ενέργειες. ϒπενθυμίζουμε ότι
στο μη σχετικιστικό όριο Thomson ισχύουν τα αντίθετα. Οι συγκρούσεις
ηλεκτρονίων-φωτονίων είναι πιο συχνές αλλά τα ηλεκτρόνια χάνουν ένα μικρό μέρος
της ενέργειάς τους σε κάθε σύγκρουση. Μία σε βάθος ανάλυση του ορίου
Klein-Nishina ξεφεύγει του παρόντος καθώς η ενεργειακή εξάρτηση της ενεργού
διατομής κάνει τους υπολογισμούς πολύπλοκους. Εδώ θα παρουσιάσουμε
μόνο έναν απλό τρόπο για να υπολογίσουμε τις ενεργητικές απώλειες των
ηλεκτρονίων.
΄Εστω λοιπόν ότι μονοενεργητικά ηλεκτρόνια ενέργειας γmec2 εισέρχονται σε
μονοχρωματικό πεδίο φωτονίων χαρακτηριστικής ενέργειας ϵ0 και αριθμητικής
πυκνότητας n0 και έστω ότι ισχύει γϵ0 >> mec2. Σύμφωνα με τα όσα αναφέραμε
στην παράγραφο 5.3.3 οι ενεργειακές απώλειες των ηλεκτρονίων δίνονται από τη
σχέση
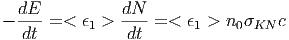 |
Εάν λοιπόν θέσουμε < ϵ1 >≈ γmec2 και χρησιμοποιήσουμε τη σχέση (5.10) παίρνουμε
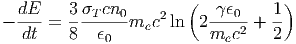 | (5.44) |
Συγκρίνοντας την παραπάνω σχέση με τη σχέση (5.29) διαπιστώνουμε ότι όσο αυξάνεται η ενέργεια των ηλεκτρονίων και ο σκεδασμός κινείται από το μη σχετικιστικό στο σχετικιστικό όριο, οι ενεργειακές απώλειες των ηλεκτρονίων ουσιαστικά γίνονται σχεδόν ανεξάρτητες της ενέργειας των ηλεκτρονίων. Δεν θα ασχοληθούμε άλλο εδώ με το όριο Klein-Nishina παρόλο που αυτό συναντάται συχνά στην Αστροφυσική ϒψηλών Ενεργειών, με αποτέλεσμα βέβαια να δυσχεραίνει σημαντικά τους υπολογισμούς.
Να ολοκληρώσετε ως προς στερεά γωνία τη σχέση (5.2) για να βρείτε τη σχέση (5.1). ϒπενθυμίζεται ότι dΩ = sin ΘdΘdϕ.
Ολοκληρώνοντας τη σχέση (5.9) ως προς στερεά γωνία να δείξετε ότι η ολική ενεργός διατομή στην περίπτωση μη πολωμένης ακτινοβολίας ισούται με σT .
Να δειχθεί ότι στο σύστημα ηρεμίας του ηλεκτρονίου Κ΄ τα φωτόνια προσπίπτουν σε έναν στενό κώνο που έχει για άξονα τον αρνητικό άξονα των x΄ και άνοιγμα γ-1. (ϒπόδειξη: Να εξετάσετε τι συμβαίνει για ένα φωτόνιο που προσπίπτει σχηματίζοντας ορθή γωνία με τη διεύθυνση του ηλεκτρονίου στο σύστημα Κ).
Να αποδειχθεί η σχέση (5.22). (ϒπόδειξη: Να ξεκινήσετε από τη σχέση (5.4) και να χρησιμοποιήσετε το γεγονός ότι η ακτινοβολούμενη ισχύς P ισούται με τις ενεργειακές απώλειες του ηλεκτρονίου καθώς και το ότι η ενεργειακή πυκνότητα των φωτονίων δίνεται από τη σχέση uφωτ′ = ∑ iEi2∕8π, όπου E i είναι οι εντάσεις των ηλεκτρομαγνητικών κυμάτων που σκεδάζονται από το ηλεκτρόνιο).
Να βρεθεί ο συντελεστής στη σχέση (5.40).
Να αποδειχτεί η σχέση (5.41).
Δίνεται η σχέση
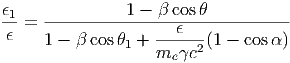 | (5.45) |
όπου ϵ, ϵ1 είναι οι ενέργειες του φωτονίου prin και met τη σκέδαση αντίστοιχα, μετρημένες στο σύστημα του εργαστηρίου. Επίσης α είναι η γωνία που σχηματίζουν οι διευθύνσεις των ορμών του φωτονίου πριν και μετά τη σκέδαση.
| Περιοχή ΗΜ φάσματος | Συχνότητα στόχου | Συχνότητα φωτονίου μετά |
| ν (Hz) | τη σκέδαση ν1 (Hz) | |
| Ραδιοκύματα | 109 | |
| Μακρινό ϒπέρυθρο | 3 × 1012 | |
| Οπτικό | 4 × 1014 | |
Η πλήρης έκφραση για την ενεργό διατομή του αντίστροφου σκεδασμού Compton είναι:
![[ ′[ ′ ′ ] ′ ]
σ = 3- 1 +-x- 2x-(1-+-x-)- ln(1 + 2x ′) + -1- ln(1 + 2x ′) - -1-+-3x--- ,
4 x′3 1 + 2x′ 2x′ (1 + 2x′)2](HEA_files/HEA121x.png) |
όπου x′ = ϵ′∕mec2 είναι η αδιάστατη ενέργεια του φωτονίου στο σύστημα ηρεμίας του ηλεκτρονίου.
Με χρήση αναπτύγματος Taylor να βρείτε τις προσεγγιστικές εκφράσεις για την ενεργό διατομή στα δύο παραπάνω όρια. (ϒπόδειξη: για το όριο Thomson θα χρειαστεί να κρατήσετε μέχρι και 3ης τάξης όρους σε ορισμένα αναπτύγματα για να βρείτε ότι σ ≈ σT .)
Δεδομένου ότι ο ρυθμός απώλειας ενέργειας ενός ηλεκτρονίου με παράγοντα Lorentz γ λόγω αντίστροφου σκεδασμού Compton είναι
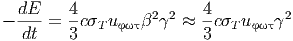 |
να εκτιμήσετε τον χρόνο ζωής (συναρτήσει του γ) ενός ηλεκτρονίου που κινείται εντός του μικροκυματικού υποβάθρου ακτινοβολίας. (Δίνεται ότι η θερμοκρασία του υποβάθρου είναι T = 2.7 Κ.)
Η συνάρτηση που μας δίνει το φάσμα στην περίπτωση μονοενεργειακών ηλεκτρονίων και φωτονίων δίνεται από τη σχέση (5.34) για το όριο Thomson. Μπορεί να προσεγγιστεί με μια συνάρτηση δέλτα περί τη μέση ενέργεια, δηλαδή
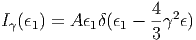 |
Βρείτε ποια είναι η σταθερά A απαιτώντας ο ρυθμός της ακτινοβολούμενης ενέργειας των φωτονίων να ισούται με τον ρυθμό απώλειας ενέργειας του ηλεκτρονίου.
Αν έχουμε ηλεκτρόνια νόμου δύναμης
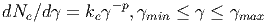 |
να γράψετε πώς υπολογίζεται το φάσμα για ένα αυθαίρετο πεδίο φωτονίων n(ϵ). Για μονοχρωματικά φωτόνια προκύπτει ένα φάσμα επίσης της μορφής νόμου δύναμης με δείκτη α = (p - 1)∕2. Να δειχθεί. Ποια τα όρια αυτού; Αν το σκεδαζόμενο πεδίο φωτονίων είναι μέλαν σώμα, ποια η μορφή του φάσματος;
ϒποθέστε ότι ηλεκτρόνια επιταχύνονται από ένα σταθερό ηλεκτρικό πεδίο
έντασης E statvolt / cm. Στο ίδιο περιβάλλον υπάρχει ένα λουτρό φωτονίων,
αριθμητικής πυκνότητας nγ και ενέργειας < Ex > στο σύστημα εργαστηρίου.
Η ενεργός διατομή για αντίστροφο σκεδασμό Compton δίνεται από την ΄Ασκηση
10. Το κάθε ηλεκτρόνιο ξεκινάει με μηδενική ταχύτητα, οπότε, εφόσον έχει
διανύσει απόσταση d στο ηλεκτρικό πεδίο, η ενέργεια που θα έχει αποκτήσει
θα είναι E = eEd.
1. Ορίσατε το xmax συναρτήσει του ηλεκτρικού πεδίου, της ενέργειας < Ex >
και της απόστασης d, όπου x = ϵ′∕mec2 είναι η αδιάστατη ενέργεια ενός
φωτονίου όπως αυτή μετράται στο σύστημα ηρεμίας του ηλεκτρονίου. Αν
υποθέσουμε ότι xmax » 1, υπολογίστε (με ακρίβεια τάξης μεγέθους) το
οπτικό βάθος για αντίστροφο σκεδασμό Compton. Θεωρήστε την αριθμητική
πυκνότητα nγ γνωστή.
2. ϒποθέστε ότι τα φωτόνια παράγονται κοντά σε μία κεντρική πηγή
λαμπρότητας L, ώστε σε απόσταση R από αυτήν η αριθμητική πυκνότητα
φωτονίων να είναι nγ = L∕(4πR2c < E
x >). ϒπολογίστε ξανά (με ακρίβεια
τάξης μεγέθους) το οπτικό βάθος για αντίστροφο σκεδασμό Compton. Λύστε
για d = 0.1R, R = 108 cm, L = 1037 erg s-1, < E
x >= 1000 eV, και
E = 104 statvolt cm-1. (1 statvolt = 300 Volt, 1 statcoulomb = 1∕3 × 10-9
Coulomb, Volt = Joule/Coulomb.) Πως εκτιμάτε τις δυνατότητες επιτάχυνσης
ηλεκτρονίων σε αυτό το σύστημα;
Ο Geminga pulsar (σχήμα 5.10) παρατηρήθηκε στις ακτίνες γ κατά τη
δεκαετία του 1990. Η περίοδος περιστροφής του είναι 0.237 s με
Ṗ = 1.097 × 10-14, η δε απόστασή του από εμάς είναι D = 552 ly (1 parsec =
3.26 ly). Η εκπομπή του στις ακτίνες γ υπερβαίνει κατά 3 τάξεις μεγέθους την
εκπομπή του στις ακτίνες Χ και κατά 9 τάξεις μεγέθους τη ραδιοεκπομπή. Μία
εξήγηση της εκπομπής αυτής είναι ο αντίστροφος σκεδασμός Compton από
σχετικιστικά ηλεκτρόνια που επιταχύνονται στη μαγνητόσφαιρα του Geminga
και σκεδάζουν θερμικά φωτόνια, που εκπέμπονται στις ακτίνες Χ. Ξεκινώντας
από αυτήν την υπόθεση μπορούμε να εκτιμήσουμε την ενεργειακή κατανομή
των σχετικιστικών ηλεκτρονίων που θα χρειαζόταν το μοντέλο για να
λειτουργήσει.
1) Ο νόμος δύναμης που παρατηρούμε στις ακτίνες γ έχει φασματικό δείκτη
a = 0.5. Αυτό σημαίνει ότι τα ηλεκτρόνια θα πρέπει να έχουν κατανομή νόμου
δύναμης με εκθέτη που δίνεται από τη σχέση a = 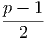 , άρα p = 2.
, άρα p = 2.
2) Από τις παρατηρήσεις στις ακτίνες Χ, διαπιστώνεται ότι το φάσμα εκεί μπορεί
να προσεγγιστεί με μία συνάρτηση δ (μονοχρωματική εκπομπή) της μορφής
A0δ(ν - ν0) με A0 = 1011Jy Hz και ν
0 = 1017Hz. (1 Jy = 10-23 erg s-1
cm-2 Hz-1). Εάν θεωρήσουμε τα φωτόνια αυτά σαν τα φωτόνια χαμηλών
ενεργειών για τον αντίστροφο σκεδασμό Compton, τότε από τις σχέσεις
ϵ1min = 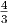 ϵ0γmin2 και ϵ
1max =
ϵ0γmin2 και ϵ
1max = 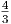 ϵ0γmax2 βρείτε τα γ
min και γmax για ν1min = 1022Hz
και ν1max = 1024Hz.
ϵ0γmax2 βρείτε τα γ
min και γmax για ν1min = 1022Hz
και ν1max = 1024Hz.
3) Για να βρούμε την αριθμητική πυκνότητα n0 των φωτονίων στις ακτίνες Χ
θεωρούμε ότι προέρχονται από την επιφάνεια του αστέρα, οπότε γράφουμε
L0 = 4πR⋆2cu
0 = 4πR⋆2chν
0n0, όπου L0 είναι η λαμπρότητα στις ακτίνες Χ, R⋆ η
ακτίνα του αστέρα νετρονίων και u0 = hν0n0 η ενεργειακή πυκνότητα των
ακτίνων Χ. Η λαμπρότητα λαμβάνεται κατευθείαν από τις παρατηρήσεις μας,
L0 = 4πD2 ∫ dνF
o = 4πD2A
0. Οπότε, χρησιμοποιώντας και ότι R⋆ = 106cm,
μπορείτε να υπολογίσετε το n0;
4) Από τη σχέση Ipl(ϵ1) = 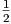 ken0σT cϵ0p-1
2 ϵ11p-1
2 και το n0 μπορούμε να βρούμε
τη σταθερά ke των ηλεκτρονίων. Από το φάσμα έχουμε ότι ν1 = 1024Hz,
νFν = 1014JyHz, και συνεπώς η ένταση ακτινοβολίας στη μαγνητόσφαιρα του
pulsar θα είναι Iν = 4πD2F
ν = 5 × 1035erg∕s∕Hz. Μπορούμε πλέον να λύσουμε
την αρχική σχέση ως προς ke (κάντε το). Η συνολική ενέργεια που υπάρχει
στα ηλεκτρόνια δίνεται από τη σχέση Etot = ∫
γminγmax
dγ ⋅ γmec2N(γ).
Χρησιμοποιώντας τη σχέση N(γ) = keγ-p για γ
min ≤ γ ≤ γmax μπορείτε να
υπολογίσετε το Etot;
ken0σT cϵ0p-1
2 ϵ11p-1
2 και το n0 μπορούμε να βρούμε
τη σταθερά ke των ηλεκτρονίων. Από το φάσμα έχουμε ότι ν1 = 1024Hz,
νFν = 1014JyHz, και συνεπώς η ένταση ακτινοβολίας στη μαγνητόσφαιρα του
pulsar θα είναι Iν = 4πD2F
ν = 5 × 1035erg∕s∕Hz. Μπορούμε πλέον να λύσουμε
την αρχική σχέση ως προς ke (κάντε το). Η συνολική ενέργεια που υπάρχει
στα ηλεκτρόνια δίνεται από τη σχέση Etot = ∫
γminγmax
dγ ⋅ γmec2N(γ).
Χρησιμοποιώντας τη σχέση N(γ) = keγ-p για γ
min ≤ γ ≤ γmax μπορείτε να
υπολογίσετε το Etot;
5) Οι ενεργειακές απώλειες των ηλεκτρονίων δίνονται από τη σχέση
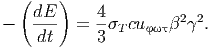
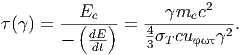
6) Η συνολική λαμπρότητα του pulsar στις ακτίνες γ είναι Lγ = 4πD2 ∫ ν1ν2 dνFν ≈ 7 × 1033 erg/s. Ο ρυθμός ακτινοβολίας περιστρεφόμενου δίπολου, όμως, για τις παραμέτρους του Geminga pulsar μας δίνει Ė = 1.2 × 1034 erg/s. Συγκρίνοντας τα δύο μεγέθη μπορούμε να παρατηρήσουμε το ποσοστό της συνολικά ακτινοβολούμενης ενέργειας που μετατρέπεται σε ακτίνες γ.
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press
(3rd edition).
Blumenthal, G. B., & Gould, R. J. (1970). “Bremsstrahlung, Synchrotron
Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute
Gases”. Reviews of Modern Physics 42, 237.
Η ακτινοβολία σύγχροτρον αποτελεί αναμφίβολα τον πιο συχνά απαντώμενο μηχανισμό μη θερμικής ακτινοβολίας στην Αστροφυσική. ΄Οπως αναφέραμε και στο Κεφάλαιο 2 πολλές παρατηρήσεις αποδίδονται σε αυτή: Ακτινοβολία από υπολείμματα υπερκαινοφανών, από pulsars, από τον δίσκο τόσο του Γαλαξία μας όσο και αυτού άλλων γαλαξιών καθώς και από πυρήνες, πίδακες και ραδιολοβούς Ενεργών Γαλαξιών. Σε αυτό το κεφάλαιο θα εξετάσουμε τα κυριότερα γνωρίσματα του μηχανισμού όπως τις ενεργειακές απώλειες των σωματίων που ακτινοβολούν και το δημιουργούμενο φάσμα εκπομπής. Επίσης θα δώσουμε μια σειρά αστροφυσικών εφαρμογών.
Ο μηχανισμός σύγχροτρον, σε αντίθεση με τον σκεδασμό Compton, αποτελεί έναν «γνήσιο» μηχανισμό εκπομπής φωτονίων1 . Η ακτινοβολία αυτή δημιουργείται από την κίνηση σχετικιστικών ηλεκτρονίων μέσα σε μαγνητικά πεδία. Τα ηλεκτρόνια επιταχύνονται καθώς διαγράφουν ελικοειδείς τροχιές και αποτέλεσμα αυτής της επιτάχυνσης είναι η ακτινοβολία σύγχροτρον. Μία πλήρης παρουσίαση της σχετικής θεωρίας ξεφεύγει των ορίων του παρόντος. Εδώ θα παρουσιάσουμε μόνο τα αναγκαία εκείνα στοιχεία που είναι απαραίτητα για μια πρώτη κατανόηση του μηχανισμού αυτού. Το σημείο αφετηρίας είναι η σχέση Larmor γενικευμένη κατάλληλα ώστε να περιλαμβάνει και την περίπτωση ακτινοβολίας σχετικιστικών σωματίων. Αυτή γράφεται:
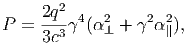 | (6.1) |
όπου P η ακτινοβολούμενη ισχύς του φορτίου q που κινείται με παράγοντα Lorentz γ και α⊥, α∥ οι συνιστώσες της επιτάχυνσης κάθετα και παράλληλα στο άνυσμα της ταχύτητας (βλ. και ΄Ασκηση 6.1).
Για να μπορέσουμε να χρησιμοποιήσουμε τη σχέση (6.1) απαιτείται να υπολογίσουμε την επιτάχυνση του σωματίου καθώς αυτό κινείται σε μαγνητικό πεδίο έντασης B [βλ. Σχήμα 6.1]. Από τη σχετικιστική μορφή της εξίσωσης του Νεύτωνα έχουμε
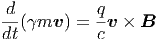 | (6.2) |
η οποία στη συγκεκριμένη περίπτωση γράφεται
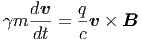 | (6.3) |
Επειδή η κάθετη συνιστώσα της επιτάχυνσης δίνεται από τη σχέση α⊥ = ωBv⊥, αντικαθιστώντας στην (6.1) παίρνουμε με τη βοήθεια της (6.3)
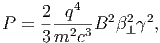 | (6.4) |
όπου β⊥ = v⊥∕c = v sin α∕c. Η γωνία α είναι η γωνία που σχηματίζεται ανάμεσα στη διεύθυνση της έντασης του μαγνητικού πεδίου και της ταχύτητας. Για ισοτροπική κατανομή των ηλεκτρονίων μπορούμε να υπολογίσουμε τη μέση τιμή του β⊥:
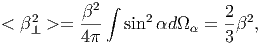 | (6.5) |
όπου dΩα η στοιχειώδης στερεά γωνία στον χώρο των ταχυτήτων.
Στην περίπτωση όπου το φορτισμένο σωμάτιο είναι ηλεκτρόνιο, τότε χρησιμοποιώντας
τις σχέσεις (5.7), (5.8) και (6.5) βρίσκουμε
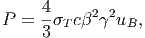 | (6.6) |
όπου uB = B2∕8π είναι η ενεργειακή πυκνότητα του μαγνητικού πεδίου. Η σχέση (6.6) δίνει τη συνολική ισχύ της εκπεμπόμενης ακτινοβολίας και κατά συνέπεια τις ενεργειακές απώλειες των σχετικιστικών ηλεκτρονίων. Χρησιμοποιώντας την μπορούμε να βρούμε τον χρόνο ζωής των ηλεκτρονίων (βλ. ανάλογη περίπτωση με τον αντίστροφο σκεδασμό Compton – σχέση 5.29)
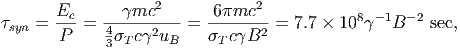 | (6.7) |
δηλαδή τα ηλεκτρόνια υψηλών ενεργειών χάνουν γρηγορότερα την ενέργειά τους από ότι αυτά που έχουν χαμηλές ενέργειες.
Σημείωση: Μία ενδιαφέρουσα ερώτηση αφορά την ακτινοβολία σύγχροτρον από φορτισμένα σωματίδια που δεν είναι ηλεκτρόνια. Με τη βοήθεια της σχέσης (6.6) είναι εύκολο να δειχτεί ότι, εάν αυτά είναι π.χ. πρωτόνια ίδιου παράγοντα Lorentz με τα ηλεκτρόνια, τότε ισχύει
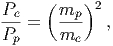 | (6.8) |
όπου Pe και Pp η ακτινοβολούμενη ισχύς των ηλεκτρονίων και των πρωτονίων, αντίστοιχα. Συνεπώς η ακτινοβολία των ηλεκτρονίων είναι πολλές τάξεις μεγέθους μεγαλύτερη από την ακτινοβολία των πρωτονίων. Εάν λοιπόν μία πηγή περιέχει σχετικιστικά ηλεκτρόνια και πρωτόνια ίδιου παράγοντα Lorentz, η ακτινοβολία των πρωτονίων μπορεί να θεωρηθεί αμελητέα σε σχέση με αυτή που παράγουν τα ηλεκτρόνια και κατά συνέπεια μη ανιχνεύσιμη. Αυτός είναι και ο λόγος που δεν γνωρίζουμε το ποσό των σχετικιστικών πρωτονίων που περιέχουν οι διάφορες πηγές υψηλών ενεργειών.
Η μέθοδος εύρεσης του συντελεστή εκπομπής της ακτινοβολίας σύγχροτρον ξεφεύγει των ορίων του παρόντος μαθήματος (για μία πλήρη απόδειξη βλ. Rybicki & Lightman, παράγραφος 6.4). Θα αρκεστούμε λοιπόν στη σκιαγράφηση μερικών βασικών νόμων και αρχών που τη διέπουν.
Ας ξεκινήσουμε από τη μη σχετικιστική περίπτωση. Το ηλεκτρόνιο διαγράφει κυκλική τροχιά με συχνότητα ωcycl = eB∕mec και η ακτινοβολία του είναι όλη σε αυτήν τη συχνότητα. Αυτή είναι η γνωστή ακτινοβολία κύκλοτρον που αποτελεί τη μη σχετικιστική εκδοχή της σύγχροτρον, η δε συχνότητα ωcycl ονομάζεται συχνότητα κύκλοτρον.
Ποιοτικά θα μπορούσαμε να εξηγήσουμε τη μετάβαση από την ακτινοβολία κύκλοτρον στη σύγχροτρον ως εξής: Από τις σχέσεις για την αποπλάνηση του φωτός (5.11) και (5.12) μπορεί να δειχθεί ότι καθώς αυξάνει η ταχύτητα του ηλεκτρονίου, η ακτινοβολία που εκπέμπεται με μορφή δίπολου στο σύστημα ηρεμίας του (σύστημα Κ΄) αρχίζει σταδιακά να παραμορφώνεται για ακίνητο παρατηρητή (σύστημα Κ) – βλ. σχήμα 6.2.
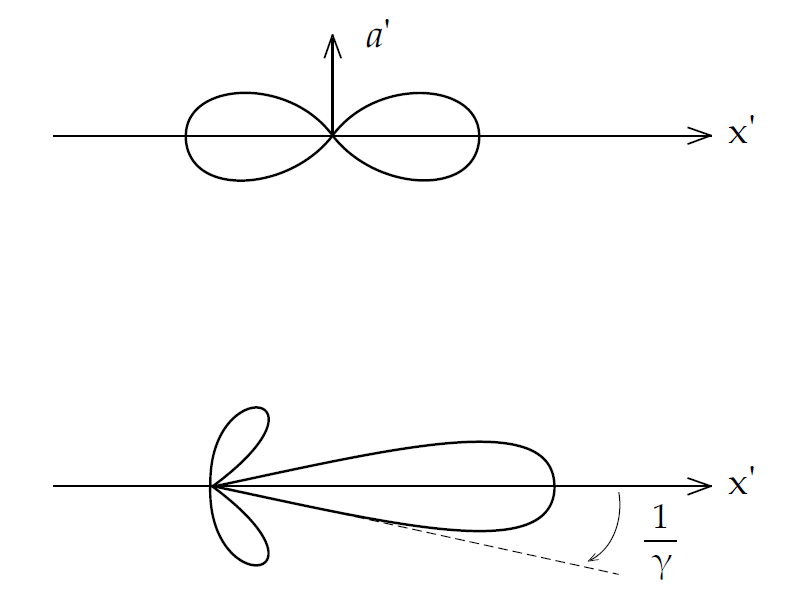
Εάν λοιπόν θεωρήσουμε μία πρώτη διόρθωση στο ηλεκτρικό πεδίο (και κατά συνέπεια στο πεδίο ακτινοβολίας) λόγω της μη αμελητέας ταχύτητας του ηλεκτρονίου, τότε είναι δυνατόν να δειχθεί ότι το ηλεκτρόνιο αρχίζει να ακτινοβολεί σε μια σειρά αρμονικές της βασικής γυροσυχνότητας ωB. ΄Οσο αυξάνεται η ταχύτητα του ηλεκτρονίου τόσο αυξάνεται το πλάτος αυτών των αρμονικών και το φάσμα από γραμμικό γίνεται σταδιακά συνεχές. Αυτό φαίνεται στο σχήμα 6.3 όπου παρουσιάζεται το φάσμα των αρμονικών τις οποίες εκπέμπει ένα σχετικιστικό ηλεκτρόνιο.
Το ζητούμενο είναι να βρούμε τη μέγιστη συχνότητα που μπορεί να εκπέμψει ηλεκτρόνιο ενέργειας γmec2 κινούμενο σε μαγνητικό πεδίο έντασης B. ΄Οπως αποδεικνύεται από τη θεωρία της ακτινοβολίας, με τη βοήθεια των μετασχηματισμών Fourier (βλ. Rybicki & Lightman, παράγραφος 2.3), εάν ένας ηλεκτρομαγνητικός παλμός έχει χρονική διάρκεια Δt, τότε η εκπομπή φτάνει μέχρι συχνότητες της τάξης ωmax ~ Δt-1, δηλαδή οι αρμονικές εκτείνονται σε υψηλότερες συχνότητες για βραχύβιους παλμούς.
΄Εστω Δθ το άνοιγμα του κώνου μέσα στον οποίο ακτινοβολεί το ηλεκτρόνιο. Ο παρατηρητής θα λαμβάνει εκπομπή όσο αυτό βρίσκεται ανάμεσα στις θέσεις 1 και 2 [βλ. σχήμα 6.4]. Ζητάμε λοιπόν τη διάρκεια του παλμού όπως την μετράει ένας ακίνητος παρατηρητής. Αυτή προφανώς είναι διαφορετική από τον χρόνο Δt που χρειάζεται το ηλεκτρόνιο να φτάσει από τη θέση 1 στη θέση 2.
Η εξίσωση (6.3) γράφεται κατά μέτρο και για μικρές διαφορές Δv, Δt
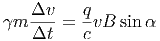 |
Χρησιμοποιώντας τη γνωστή σχέση |Δv| = Δv = vΔθ και τον ορισμό της γυροσυχνότητας, σχέση (6.29), βρίσκουμε
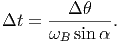 |
΄Οπως όμως προκύπτει από την σχέση (5.12), για την περίπτωσή μας ισχύει ότι Δθ ≈ 2∕γ, οπότε η παραπάνω σχέση γράφεται:
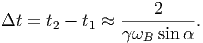 | (6.9) |
Ωστόσο η διαφορά Δt εξαρτάται από τις χρονικές στιγμές t1 και t2 που αποτελούν
τις χρονικές στιγμές εκπομπής του παλμού. Η χρονική διαφορά που θα μετρήσει ο
παρατηρητής θα είναι σημαντικά μικρότερη γιατί το σωματίδιο κινείται προς τη
διεύθυνση του παρατηρητή και με ταχύτητα σχεδόν ίση με την ταχύτητα του
φωτός2 .
Αφήνεται ως άσκηση να δειχτεί ότι εάν Δ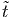 η χρονική διαφορά των χρόνων άφιξης,
τότε ισχύει:
η χρονική διαφορά των χρόνων άφιξης,
τότε ισχύει:
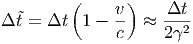 | (6.10) |
Συνεπώς, σύμφωνα με τα όσα αναφέραμε προηγουμένως για τη μέγιστη συχνότητα,
έχουμε ωmax ~ Δ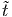 -1 ≈ γ3ω
B sin α. Εάν επιπλέον χρησιμοποιήσουμε τη σχέση
(6.29) και θέσουμε ω = 2πν, βρίσκουμε
-1 ≈ γ3ω
B sin α. Εάν επιπλέον χρησιμοποιήσουμε τη σχέση
(6.29) και θέσουμε ω = 2πν, βρίσκουμε
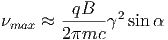 | (6.11) |
που αποτελεί και μία πρώτη ποιοτική προσέγγιση της μέγιστης συχνότητας
εκπομπής.
΄Οπως λεπτομερείς υπολογισμοί
αποδεικνύουν3
το φάσμα που ακτινοβολείται από μονοενεργητικά ηλεκτρόνια δίνεται από τη
σχέση
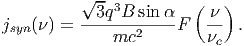 | (6.12) |
Η συχνότητα νc ονομάζεται κρίσιμη και δίνεται από τη σχέση:
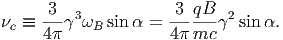 | (6.13) |
Η συνάρτηση F(x) είναι μία από τις λεγόμενες ειδικές συναρτήσεις και για λόγους πληρότητας δίνουμε τον ορισμό της
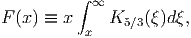 |
όπου K5∕3(ξ) είναι η τροποποιημένη συνάρτηση Bessel. Ενδιαφέρον παρουσιάζουν οι
ασυμπτωτικές μορφές της F(x):
| F(x) ∝ x1∕3 για x « 1 | ||
| F(x) ∝ e-xx1∕2 για x » 1, |
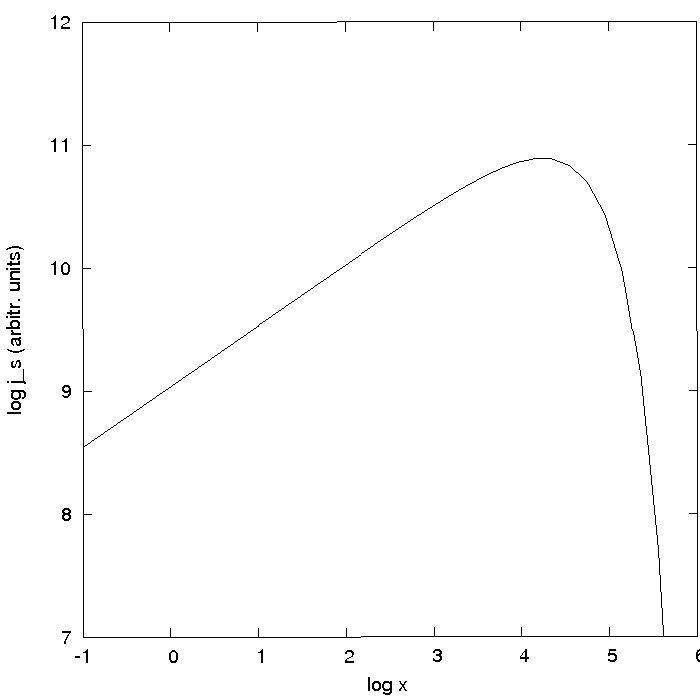
Παρατηρούμε ότι το φάσμα της ακτινοβολίας σύγχροτρον, σχέση (6.12), παρουσιάζει ένα μέγιστο που περιγράφεται κατά προσέγγιση από τη σχέση (6.13). Και οι δύο αυτές συναρτήσεις εξαρτώνται από τρεις παραμέτρους, δηλαδή τον παράγοντα Lorentz του σωματιδίου, την ένταση του μαγνητικού πεδίου και τη γωνία που σχηματίζει η ταχύτητα του σωματιδίου με το μαγνητικό πεδίο. Στις αστροφυσικές εφαρμογές αυτές οι παράμετροι είναι άγνωστες. Είναι φανερό ότι απαιτούνται, τουλάχιστον σε πρώτη προσέγγιση, μερικές υποθέσεις για να τις απαλείψουμε. Η πρώτη υπόθεση είναι προφανής και μπορεί να εφαρμοσθεί στην πλειοψηφία των αστροφυσικών πηγών. Θεωρούμε λοιπόν ότι τα ηλεκτρόνια έχουν ισοτροπική κατανομή, και συνεπώς μπορούμε να ολοκληρώσουμε το φάσμα εκπομπής (6.12) ως προς dΩα. Προσεγγιστικά μπορούμε να θεωρήσουμε ως συχνότητα της μέγιστης εκπομπής – που είναι ανεξάρτητη της γωνίας α, τη συχνότητα
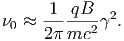 | (6.14) |
Για την περίπτωση όπου τα σωματίδια είναι ηλεκτρόνια, η παραπάνω σχέση γράφεται
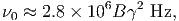 | (6.15) |
όπου το B δίνεται σε Gauss. Αυτή η σχέση, αν και προσεγγιστική, επιτρέπει μία εύκολη εκτίμηση της ενέργειας των ηλεκτρονίων που ακτινοβολούν, εάν γνωρίζουμε βέβαια την ένταση του μαγνητικού πεδίου. Θα χρησιμοποιήσουμε αυτήν τη σχέση στην παράγραφο όπου θα εξετάσουμε τις εφαρμογές της ακτινοβολίας σύγχροτρον.
΄Οπως θα δείξουμε για την ενδιαφέρουσα περίπτωση όπου τα ηλεκτρόνια έχουν κατανομή που είναι νόμος δύναμης, δηλαδή
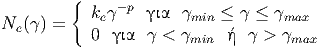 | (6.16) |
το παραγόμενο φάσμα της ακτινοβολίας σύγχροτρον έχει πολλά κοινά με αυτό του
αντίστροφου σκεδασμού Compton (βλ. παράγραφο 5.3.4).
΄Οπως και σε εκείνη την περίπτωση, το φάσμα εκπομπής των φωτονίων που
παράγεται βρίσκεται αν ολοκληρώσουμε το φάσμα ενός ηλεκτρονίου (σχέση 6.12) ως
προς όλες τις ενέργειες που αυτό μπορεί να έχει. Για να κρατήσουμε μια αναλογία με
τη σχέση (5.39) χρησιμοποιούμε την ενέργεια του εκπεμπόμενου φωτονίου αντί της
συχνότητάς του. ΄Εχουμε λοιπόν
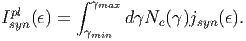 | (6.17) |
Παρόλο που το ολοκλήρωμα υπολογίζεται αναλυτικά4 , σε μία πρώτη προσέγγιση θα μπορούσαμε να θεωρήσουμε, όπως και στην ανάλογη περίπτωση του αντίστροφου σκεδασμού Compton, ότι όλη η ακτινοβολία μονοενεργητικών ηλεκτρονίων εκπέμπεται σε ενέργεια ϵ0 = hν0 (σχέση 6.14), οπότε γράφουμε
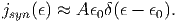 | (6.18) |
Η σταθερά A υπολογίζεται από την απαίτηση ο ρυθμός της ακτινοβολούμενης
ενέργειας να ισούται με τον ρυθμό απώλειας ενέργειας των ηλεκτρονίων που δίνεται
από τη σχέση (6.6). Με βάση τα παραπάνω μπορούμε να γράψουμε A = 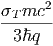 B και
η σχέση (6.17) γράφεται
B και
η σχέση (6.17) γράφεται
![[ ]p-1
pl 1σT-mc2- -ℏq 2 p-1 p-1 min max
Isyn(ϵ) = 6 qh mc B 2 ϵ 2 για ϵ1 ≤ ϵ1 ≤ ϵ1](HEA_files/HEA155x.png) | (6.19) |
όπου
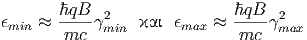 |
Η σχέση (6.19) φανερώνει ότι, όπως και στην περίπτωση του αντίστροφου σκεδασμού Compton, ηλεκτρόνια με κατανομή νόμο δύναμης εκθέτη -p δημιουργούν φωτόνια με δείκτη -(p - 1)∕2, ισχύει δηλαδή και πάλι η σχέση (5.43). Τον ίδιο νόμο δύναμης θα βρίσκαμε εάν χρησιμοποιούσαμε τη σχέση (6.12) αντί της συνάρτησης δέλτα. Αυτό φαίνεται στο σχήμα 6.6 που δείχνει τη συνέλιξη του συντελεστή εκπομπής με την κατανομή των ηλεκτρονίων. Το πρώτο (από αριστερά) είναι το φάσμα εκπομπής που δημιουργούν ηλεκτρόνια με παράγοντα Lorentz γmin, το αμέσως επόμενο αυτό που δημιουργούν ηλεκτρόνια με παράγοντα γmin + Δγ, κ.ο.κ. μέχρι το τελευταίο που δημιουργείται από ηλεκτρόνια με παράγοντες Lorentz γmax. Στο σχήμα φαίνεται ο τρόπος με τον οποίο αυτός ο αλγόριθμος δημιουργεί έναν νόμο δύναμης.
Τόσο η ακτινοβολία σύγχροτρον, όσο και ο αντίστροφος σκεδασμός Compton, αποτελούν πολύ σημαντικές φυσικές διαδικασίες καθώς όλες οι αστροφυσικές πηγές υψηλών ενεργειών περιέχουν σχετικιστικά ηλεκτρόνια, μαγνητικά πεδία και φωτόνια χαμηλών ενεργειών. Το πρώτο ερώτημα είναι ποια διαδικασία θα επικρατήσει καθώς οι δύο ανταγωνίζονται για τις ενεργειακές απώλειες των σχετικιστικών ηλεκτρονίων. Μία απλή σύγκριση των ενεργειακών απωλειών στην περίπτωση της ακτινοβολίας σύγχροτρον και του αντίστροφου σκεδασμού Compton (σχέσεις 5.29 και 6.6) δίνει
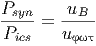 | (6.20) |
που είναι ανεξάρτητη της ενέργειας των ηλεκτρονίων. Εάν ο λόγος αυτός
είναι μεγαλύτερος της μονάδας θα επικρατήσει η ακτινοβολία σύγχροτρον,
ενώ εάν μικρότερος θα επικρατήσει ο αντίστροφος σκεδασμός Compton.
΄Ενα δεύτερο ερώτημα αφορά τη σύγκριση των ενεργειών που αυτοί οι μηχανισμοί
δημιουργούν/σκεδάζουν φωτόνια. Από τις σχέσεις (5.35) και (6.14) παρατηρούμε ότι
αυτά είναι ανάλογα του τετράγωνου της ενέργειας του ηλεκτρονίου. ΄Εστω τώρα μία
πηγή, π.χ. ένας ενεργός γαλαξίας, που περιέχει μαγνητικό πεδίο έντασης B,
υπόβαθρο μονοχρωματικών φωτονίων χαμηλής ενέργειας ϵ0 και σχετικιστικά
ηλεκτρόνια ενέργειας γmec2. Για να συγκρίνουμε καλύτερα τις ενέργειες
εκπομπής/σκεδασμού των φωτονίων τις μετατρέπουμε καταρχάς στις ίδιες μονάδες –
και μια καλή επιλογή είναι να τις εκφράσουμε σε μονάδες της μάζας ηρεμίας
του ηλεκτρόνιου mec2. Για την περίπτωση του αντίστροφου σκεδασμού
Compton έχουμε από τη σχέση (5.35) ότι το μέσο φωτόνιο σκεδάζεται σε
ενέργεια
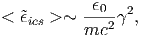 | (6.21) |
όπου έχουμε παραλείψει τον παράγοντα 4/3 για λόγους απλότητας. Από την άλλη, η ενέργεια ενός μέσου φωτονίου (σχέση 6.4) που παράγεται κατά την ακτινοβολία σύγχροτρον είναι
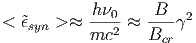 | (6.22) |
όπου Bcr = me2c3∕eℏ = 4.413 × 1013 Gauss είναι η κρίσιμη ένταση του μαγνητικού πεδίου.
Σημείωση: Η κρίσιμη ένταση του μαγνητικού πεδίου είναι εκείνη η ένταση για την οποία ένα μη σχετικιστικό σωμάτιο ακτινοβολεί τη μάζα ηρεμίας του. Πράγματι εάν αντικαταστήσουμε στη συχνότητα κύκλοτρου το B με το Bcr βρίσκουμε ℏωcycl = mc2.
Επειδή για τη συντριπτική πλειοψηφία των αστροφυσικών πηγών ισχύει B∕Bcr « ϵ0∕mc2 διαπιστώνουμε ότι ο αντίστροφος σκεδασμός Compton παράγει πολύ πιο ενεργητικά φωτόνια από ότι η ακτινοβολία σύγχροτρον παρόλο που τα ηλεκτρόνια έχουν την ίδια ενέργεια και στις δύο περιπτώσεις. Σχετικά παραδείγματα θα δοθούν αμέσως πιο κάτω στις εφαρμογές.
Εφαρμογή 1: Από ραδιοπαρατηρήσεις σε συχνότητες από 10 MHz έως 10 GHz οι
Αστροφυσικοί διαπίστωσαν ότι υπάρχει εκπομπή που είναι διάχυτη σε όλο τον
Γαλαξία. Αυτή προέρχεται από ακτινοβολία σύγχροτρον ηλεκτρονίων καθώς αυτά
κινούνται στον δίσκο και την άλω του Γαλαξία που περιέχει μαγνητικό πεδίο έντασης
B ~ 3 μGauss.
Η σχέση (6.15) μας επιτρέπει να βγάλουμε μερικά συμπεράσματα για την ενέργεια
των ηλεκτρονίων εάν γνωρίζουμε την ένταση του μαγνητικού πεδίου μέσα
στο οποίο αυτά ακτινοβολούν. Μία απλή εφαρμογή της αποδεικνύει ότι τα
ηλεκτρόνια που ακτινοβολούν σε αυτές τις συχνότητες έχουν ενέργειες
από 500 MeV έως 15 GeV. Αυτές οι παρατηρήσεις αποτελούν απόδειξη ότι
τουλάχιστον τα ηλεκτρόνια της κοσμικής ακτινοβολίας βρίσκονται παντού στον
Γαλαξία και δεν είναι απλώς ένα τοπικό φαινόμενο. Ο χρόνος ζωής των
ηλεκτρονίων αυτών υπολογίζεται, ανάλογα με την ενέργειά τους, από 80 έως 2.500
εκατομμύρια χρόνια. Ωστόσο υπάρχει ακόμα μία ενδιαφέρουσα συνέπεια των
παραπάνω συμπερασμάτων. Τα ηλεκτρόνια που παράγουν τη ραδιοεκπομπή θα
σκεδάσουν επίσης τα φωτόνια του μικροκυματικού υπόβαθρου σε ενέργειες από
ϵmin ≈ (4∕3)(2.7kTb)γmin2 ≈ 0.8 keV σε ϵ
max ≈ (4∕3)(2.7kTb)γmax2 ≈ 0.8
MeV (σχέση 5.35), που βρίσκονται στην περιοχή των ακτίνων Χ/γ – εδώ
φαίνεται και αυτό που αναφέραμε στην προηγούμενη παράγραφο σχετικά με τη
διαφορά στις ενέργειες των φωτονίων που παράγουν οι δύο μηχανισμοί.
Το ερώτημα που τίθεται είναι εάν αυτά τα φωτόνια υψηλών ενεργειών θα
έχουν κάποια αξιόλογη λαμπρότητα. Η σχέση (6.20) μας παρέχει μία άμεση
απάντηση. Πράγματι η ενεργειακή πυκνότητα του μαγνητικού πεδίου του
Γαλαξία είναι uB = B2∕8π ≈ 3.6 × 10-13 erg/cm3 ≈ 0.22 eV/cm3, ενώ η
ενεργειακή πυκνότητα των φωτονίων του μικροκυματικού υπόβαθρου είναι
ufwt = αT4 = (4σ∕c)T4 = 4 × 10-13 erg/cm3 ≈ 0.25 eV/cm3. Συμπεραίνουμε
λοιπόν ότι τα ηλεκτρόνια θα χάσουν περίπου το ίδιο ποσό της ενέργειάς τους
ακτινοβολώντας φωτόνια σύγχροτρον και σκεδάζοντας φωτόνια του μικροκυματικού
υπόβαθρου. Συνεπώς η ακτινοβολούμενη ισχύς των φωτονίων στις δύο αυτές
περιοχές θα είναι περίπου ίδια, παρόλο που οι ενέργειες των παραγόμενων φωτονίων
από τους δύο μηχανισμούς απέχουν πολλές τάξεις μεγέθους η μία από την
άλλη.
Εφαρμογή 2: Στο προηγούμενο παράδειγμα μπορέσαμε και βρήκαμε την ενέργεια των ηλεκτρονίων γιατί είναι γνωστό το μαγνητικό πεδίο του Γαλαξία μας από διάφορα άλλα δεδομένα. Ωστόσο, στις περισσότερες περιπτώσεις, η ένταση του μαγνητικού πεδίου διαφόρων κοσμικών πηγών δεν είναι γνωστή και αυτό αφήνει δύο ελεύθερες παραμέτρους στη σχέση (6.14). Για αυτό οι αστροφυσικοί υιοθετούν την υπόθεση ισοκαταμερισμού της ενέργειας που περικλείεται στο μαγνητικό πεδίο και αυτής που περικλείεται στα σωματίδια. ΄Οπως θα δείξουμε αυτή η υπόθεση ισοδυναμεί με ελαχιστοποίηση της ενέργειας που υπάρχει στην πηγή. Η ενέργεια που εμπεριέχεται στο μαγνητικό πεδίο σφαιρικής πηγής όγκου V δίνεται από τη σχέση
| Ολική ενέργεια μαγνητικού πεδίου = | ||
| = Ενεργειακή πυκνότητα μαγνητικού πεδίου × ΄Ογκος πηγής |
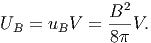 | (6.23) |
Εάν η πηγή παρουσιάζει λαμπρότητα L* σε κάποια συχνότητα παρατήρησης ν*, τότε σε πρώτη προσέγγιση το ενεργειακό της περιεχόμενο σε σχετικιστικά ηλεκτρόνια δίνεται από τη σχέση
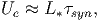 |
όπου τsyn ο χρόνος ζωής των ηλεκτρονίων με παράγοντα Lorentz γ που εκπέμπουν στη συχνότητα ν* (βλ. σχέση 6.7). Χρησιμοποιούμε στη συνέχεια τη σχέση (6.14) για να συνδέσουμε τη συχνότητα ν* με τον παράγοντα Lorentz του ηλεκτρονίου και το μαγνητικό πεδίο, υποθέτοντας μονοενεργητική εκπομπή για τα ηλεκτρόνια. ΄Εχουμε λοιπόν:
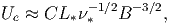 | (6.24) |
όπου C = 3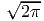 (emec)1∕2∕σ
T . Η παραπάνω σχέση εξαρτάται από δύο παρατηρησιακά
δεδομένα, δηλαδή τη συχνότητα ν* και τη λαμπρότητα της πηγής L* σε αυτή τη
συχνότητα καθώς και από μία άγνωστη ποσότητα, την ένταση του μαγνητικού
πεδίου Β. Για να προσδιορίσουμε το συνολικό ενεργειακό περιεχόμενο της πηγής
απαιτείται ακόμη να γνωρίζουμε το ενεργειακό της περιεχόμενο σε πρωτόνια Up.
Αυτό, σύμφωνα με τα όσα αναφέρθηκαν στην παράγραφο 6.2, είναι άγνωστό γιατί,
αφού τα πρωτόνια δεν ακτινοβολούν, δεν γνωρίζουμε κάτι για τα χαρακτηριστικά του
πληθυσμού τους. Μπορούμε ωστόσο να διακρίνουμε δύο ακραίες περιπτώσεις
ανάλογα με την υπόθεση που κάνουμε για τον μηχανισμό επιτάχυνσης: (α)
Τα πρωτόνια επιταχύνονται στην ταχύτητα των ηλεκτρονίων και συνεπώς
Up = (mp∕me)Ue και (β) τα πρωτόνια επιταχύνονται στην ενέργεια των
ηλεκτρονίων, οπότε Up = Ue.
(emec)1∕2∕σ
T . Η παραπάνω σχέση εξαρτάται από δύο παρατηρησιακά
δεδομένα, δηλαδή τη συχνότητα ν* και τη λαμπρότητα της πηγής L* σε αυτή τη
συχνότητα καθώς και από μία άγνωστη ποσότητα, την ένταση του μαγνητικού
πεδίου Β. Για να προσδιορίσουμε το συνολικό ενεργειακό περιεχόμενο της πηγής
απαιτείται ακόμη να γνωρίζουμε το ενεργειακό της περιεχόμενο σε πρωτόνια Up.
Αυτό, σύμφωνα με τα όσα αναφέρθηκαν στην παράγραφο 6.2, είναι άγνωστό γιατί,
αφού τα πρωτόνια δεν ακτινοβολούν, δεν γνωρίζουμε κάτι για τα χαρακτηριστικά του
πληθυσμού τους. Μπορούμε ωστόσο να διακρίνουμε δύο ακραίες περιπτώσεις
ανάλογα με την υπόθεση που κάνουμε για τον μηχανισμό επιτάχυνσης: (α)
Τα πρωτόνια επιταχύνονται στην ταχύτητα των ηλεκτρονίων και συνεπώς
Up = (mp∕me)Ue και (β) τα πρωτόνια επιταχύνονται στην ενέργεια των
ηλεκτρονίων, οπότε Up = Ue.
Συνδυάζοντας τις παραπάνω σχέσεις έχουμε Up = (1 + k)Ue με 1 ≤ k ≤ mp∕me, οπότε το ολικό ενεργειακό περιεχόμενο της πηγής γράφεται
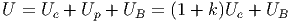 | (6.25) |
και χρησιμοποιώντας τις σχέσεις (6.23) και (6.24) μπορούμε να εκφράσουμε την ολική ενέργεια ως συνάρτηση παρατηρούμενων μεγεθών και του μαγνητικού πεδίου B
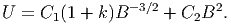 | (6.26) |
Η ελάχιστη ενέργεια δίνεται για εκείνη την τιμή του μαγνητικού πεδίου για την οποία ισχύει dU∕dB = 0. Αυτή ικανοποιείται όταν
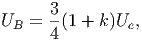 | (6.27) |
όταν δηλαδή η ενέργεια κατανέμεται (περίπου) εξίσου ανάμεσα στα ενεργητικά σωματίδια και στο μαγνητικό πεδίο. Τα παραπάνω παριστάνονται γραφικά στο σχήμα 6.7.
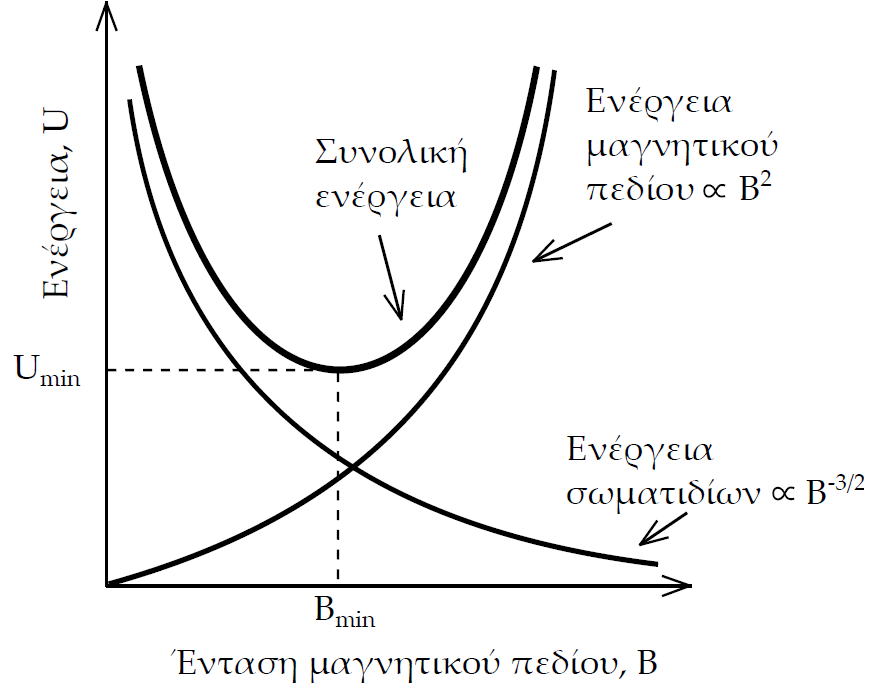
Μία εφαρμογή της παραπάνω αρχής μπορεί να γίνει στα υπολείμματα
υπερκαινοφανών. Αυτά αποτελούν τις καλύτερες υποψήφιες πηγές επιτάχυνσης της
κοσμικής ακτινοβολίας, τουλάχιστον για ενέργειες μέχρι 3 × 1015eV, που είναι η
περιοχή του λεγόμενου «γόνατου» στο φάσμα – βλ. σχήμα 2.10. Ανάμεσα στις
διάφορες ενδείξεις που έχουμε για αυτό, κεντρική θέση έχουν οι υπολογισμοί του
ενεργειακού περιεχομένου τους σε σχετικιστικά ηλεκτρόνια – το γεγονός ότι
τα υπολείμματα υπερκαινοφανών περιέχουν σχετικιστικά ηλεκτρόνια είναι
αδιαμφισβήτητο από τις ραδιοπαρατηρήσεις που τα παρουσιάζουν να έχουν μη
θερμική ακτινοβολία σύγχροτρον.
Το υπόλειμμα υπερκαινοφανούς Cassiopeia A έχει λαμπρότητα Lν ≈ 3 × 1025
erg/sec/Hz σε συχνότητα 1 GHz, ενώ η ακτίνα του είναι 1.6 pc. Με βάση
αυτά τα δεδομένα βρίσκουμε από τη σχέση (6.31) – χρησιμοποιώντας
L ≈ νLν ≈ 3 × 1034erg/sec – ότι B
min ≈ 0.13(1 + k)2∕7mGauss. Από τη σχέση
(6.15) βρίσκουμε ότι η απαιτούμενη ενέργεια των σχετικιστικών ηλεκτρονίων είναι
~800 MeV. Το ενεργειακό περιεχόμενο της πηγής σε σχετικιστικά σωματίδια
(ηλεκτρόνια και πρωτόνια) υπολογίζεται σε 4 × 1047(1 + k)4∕7 erg. Αυτό είναι ένα
σημαντικό ποσό εάν αναλογισθεί κανείς ότι ένας υπερκαινοφανής έχει κατά την
έκρηξή του κινητική ενέργεια ~ 1051erg. Συνεπώς η έκρηξη του υπερκαινοφανούς
μπορεί να μετατρέψει, κατά κάποιο τρόπο, ένα ποσοστό του αρχικού ενεργειακού του
προϋπολογισμού σε μη θερμική ενέργεια. Αυτό εξετάζεται με λεπτομέρεια
στο Κεφάλαιο 8. Παρατηρησιακά δεδομένα αλλά και θεωρητικές έρευνες
υποδεικνύουν ότι τα σχετικιστικά ηλεκτρόνια επιταχύνονται στα ισχυρά κύματα
κρούσης που δημιουργούνται κατά την έκρηξη – πράγματι το υλικό του
υπερκαινοφανούς κινείται κατά τα πρώτα 300-1000 χρόνια με ταχύτητες ~10.000
km/sec ενώ η ταχύτητα του ήχου στο μεσοαστρικό υλικό είναι μόλις 10
km/sec, συνεπώς το ωστικό κύμα που δημιουργείται έχει υψηλό αριθμό
Mach.
Σημείωση: Από τους υπολογισμούς που κάναμε παραπάνω φαίνεται ότι η
ενέργεια των ηλεκτρονίων που παράγουν τη ραδιοεκπομπή είναι της τάξης ~GeV.
Αυτές οι ενέργειες είναι μεν σχετικιστικές, δεν μπορούν όμως να συγκριθούν με
τις ενέργειες της Κοσμικής Ακτινοβολίας στο «γόνατο» που φτάνουν έως
3 × 1015eV, βλ. σχήμα 2.10. Μία νέα διάσταση του προβλήματος έδωσαν το 1996
παρατηρήσεις του ιαπωνικού ανιχνευτή ακτίνων X ASCA. Αυτός ανακάλυψε μη
θερμικές5
ακτίνες Χ από ορισμένα υπολείμματα υπερκαινοφανών που εκτείνονται έως 30 keV.
΄Ολες οι ενδείξεις συγκλίνουν στο ότι η ακτινοβολία αυτή είναι σύγχροτρον. Σε αυτή
την περίπτωση μία ακόμα εφαρμογή της σχέσης (6.15) ανεβάζει την ενέργεια των
ηλεκτρονίων σε ~70 – 100 TeV που είναι πολύ κοντά στις ζητούμενες.
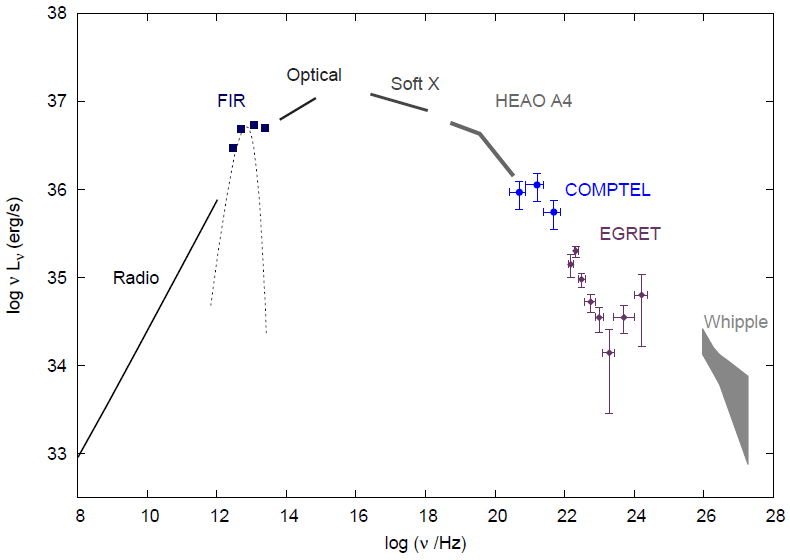
Εφαρμογή 3: Αναμφίβολα η μη θερμική πηγή με το καλύτερα παρατηρούμενο φάσμα είναι το Νεφέλωμα του Καρκίνου [σχήμα 6.8]. Το φάσμα της εκτείνεται 21 τάξεις μεγέθους, από τα ραδιοκύματα έως τις ακτίνες γ πολύ υψηλών ενεργειών. Η πηγή αυτή είναι το υπόλειμμα της έκρηξης ενός υπερκαινοφανούς το 1054 μ.Χ. στον αστερισμό του Ταύρου. Πηγή ενέργειάς του είναι ο Crab pulsar που περιστρέφεται 190 φορές το δευτερόλεπτο. Η ακτινοβολία από συχνότητες~ 108 Hz έως 1023 Hz προέρχεται από ακτινοβολία σύγχροτρον6 , ενώ οι ακόμα μεγαλύτερες συχνότητες παράγονται από αντίστροφο σκεδασμό Compton. Το μαγνητικό πεδίο του υπολείμματος υπολογίζεται σε ~1 mGauss, που σημαίνει ότι η υψηλότερη ενέργεια των ηλεκτρονίων είναι της τάξης των ~ 3 PeV, ενώ τα ραδιοκύματα δημιουργούνται από ηλεκτρόνια ~100 MeV. Παρατηρούμε επίσης ότι το φάσμα του αποτελείται από νόμο δύναμης με μεταβαλλόμενο δείκτη που μάλιστα αυξάνει όσο αυξάνει η ενέργεια. Αυτό οφείλεται πιθανότατα στους διαφορετικούς χρόνους γήρανσης των ηλεκτρονίων που ακτινοβολούν. Πράγματι από τη σχέση (6.7) συνάγουμε ότι για τα χαμηλής ενέργειας ηλεκτρόνια ο χρόνος ζωής είναι περί τα 100.000 χρόνια, που είναι πολύ μεγαλύτερος της ηλικίας του υπολείμματος (~1.000 χρόνια). Αντίθετα τα ηλεκτρόνια υψηλών ενεργειών έχουν χρόνο ζωής περί τη μία ημέρα. Αυτό πρακτικά σημαίνει ότι τα χαμηλής ενέργειας ηλεκτρόνια δεν έχουν προλάβει ακόμα να ακτινοβολήσουν ένα σημαντικό μέρος της ενέργειάς τους, ενώ αντίθετα για τα ηλεκτρόνια υψηλών ενεργειών απαιτείται συνεχής ανανέωση. Αυτές οι διαφορές οδηγούν στο ενδιαφέρον πρόβλημα της εξέλιξης των σχετικιστικών ηλεκτρονίων και προκαλούν τη συγκεκριμένη μορφή του φάσματος εκπομπής του νεφελώματος.
Ξεκινώντας από τη μη σχετικιστική εξίσωση του Larmor P = 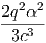 (όπου P η
ακτινοβολούμενη ισχύς, q το φορτίο του σωματιδίου και a η επιτάχυνσή
του) να δείξετε ότι αυτή γενικεύεται για σχετικιστικές ταχύτητες με τη
σχέση
(όπου P η
ακτινοβολούμενη ισχύς, q το φορτίο του σωματιδίου και a η επιτάχυνσή
του) να δείξετε ότι αυτή γενικεύεται για σχετικιστικές ταχύτητες με τη
σχέση
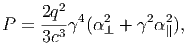 | (6.28) |
όπου α⊥ και α∥ οι συνιστώσες της επιτάχυνσης κάθετα και παράλληλα στο άνυσμα
της ταχύτητας v ενώ γ = 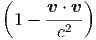 -1∕2 είναι ο παράγοντας Lorentz του
σωματιδίου.
-1∕2 είναι ο παράγοντας Lorentz του
σωματιδίου.
ϒπόδειξη: Στο στιγμιαίο σύστημα ηρεμίας Κ΄ του σωματιδίου ισχύει προφανώς η
σχέση P′ = 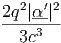 όπου P′ η ισχύς και |α′| το μέτρο του τετρανύσματος της
επιτάχυνσης. Εάν P είναι η ισχύς ως προς σύστημα ακίνητου παρατηρητή Κ, τότε
να δειχθεί ότι P = P′ και ότι το τετράνυσμα της επιτάχυνσης έχει μέτρο
|α′|2 = γ4
όπου P′ η ισχύς και |α′| το μέτρο του τετρανύσματος της
επιτάχυνσης. Εάν P είναι η ισχύς ως προς σύστημα ακίνητου παρατηρητή Κ, τότε
να δειχθεί ότι P = P′ και ότι το τετράνυσμα της επιτάχυνσης έχει μέτρο
|α′|2 = γ4![[ ( )]
α2 + γ2 vα--
c2](HEA_files/HEA171x.png) όπου α η (συνήθης) επιτάχυνση και η ταχύτητα του
συστήματος Κ΄ ως προς το σύστημα Κ.
όπου α η (συνήθης) επιτάχυνση και η ταχύτητα του
συστήματος Κ΄ ως προς το σύστημα Κ.
Να λυθεί η εξίσωση (6.3) και να δειχθεί ότι το σωμάτιο εκτελεί ελικοειδή κίνηση [βλ. σχήμα 6.1] με συχνότητα περιστροφής (γυροσυχνότητα)
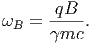 | (6.29) |
Επίσης να δειχθεί ότι η γυροακτίνα του σωματιδίου δίνεται από τη σχέση
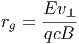 | (6.30) |
όπου E η ενέργεια του σωματιδίου και v⊥ η συνιστώσα της ταχύτητας που είναι κάθετη στη διεύθυνση του μαγνητικού πεδίου.
Να αποδείξετε τη σχέση (6.6).
Να λυθεί η διαφορική εξίσωση -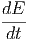 = P =
= P = 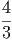 σT cγ2u
B με αρχικές συνθήκες
γ(t = 0) = γ0. Στη συνέχεια να αντικατασταθεί ο χρόνος με την έκφραση από
τη σχέση (6.7) και να δειχθεί ότι γ(τsyn) = γ0.
σT cγ2u
B με αρχικές συνθήκες
γ(t = 0) = γ0. Στη συνέχεια να αντικατασταθεί ο χρόνος με την έκφραση από
τη σχέση (6.7) και να δειχθεί ότι γ(τsyn) = γ0.
΄Εστω πηγή, η οποία εκπέμπει ισοτροπικά στο σύστημα αναφοράς της K′. Να βρεθεί εάν διατηρεί την ισοτροπία της στο σύστημα αναφοράς K το οποίο κινείται με ταχύτητα u ως προς το K′.
Να δειχθεί στη σχέση 6.18 το A = 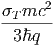 B.
B.
Να αποδειχτεί η σχέση (6.19).
Να αποδείξετε ότι εάν ένας πληθυσμός σχετικιστικών ηλεκτρονίων και πρωτονίων έχει την ίδια ταχύτητα, τότε οι ενεργειακές τους πυκνότητες συνδέονται με τη σχέση up = (mp∕me)ue. Αντίθετα, εάν έχουν την ίδια ενέργεια, τότε ισχύει up - ue.
Ξεκινώντας από τη σχέση (6.26) να αποδείξετε την (6.27). Σε αυτήν την περίπτωση το μαγνητικό πεδίο δίνεται από τη σχέση
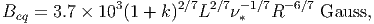 | (6.31) |
όπου R η ακτίνα της πηγής (θεωρούμενης ως σφαιρικής).
Να υπολογίσετε την κινητική ενέργεια των ηλεκτρονίων που κινούνται με την ταχύτητα της έκρηξης. Θα μπορούσαν αυτά να δημιουργούν τη ραδιοεκπομπή;
Να αποδείξετε ότι η τροχιά ενός σχετικιστικού σωματιδίου εντός ενός ομογενούς μαγνητικού πεδίου είναι ελικοειδής. ϒπόδειξη: Θεωρήστε ότι B = B0ẑ και ότι το σωματίδιο ξεκινάει από την αρχή των αξόνων με ταχύτητα u0 = (ux0, 0,uz0). Κατα μήκος των δυναμικών γραμμών, τι ισχύς εκπέμπεται;
Οι κοσμικές ακτίνες αποτελούνται κατά κύριο λόγο από πρωτόνια και
βαρύτερους πυρήνες. Ασφαλώς, όμως, θα πρέπει να υπάρχουν και κάποια
ηλεκτρόνια. Τι περιμένουμε από αυτά; Οι υψηλότερες ενέργειες κοσμικών
ακτίνων φτάνουν τα Ep,max = 1021 eV. Αν υποθέσουμε ότι τα ηλεκτρόνια
φτάνουν μέχρι Ee,max = 1020 eV, αυτά πρέπει να μετακινηθούν μέσα στο
μαγνητικό πεδίο του διαγαλαξιακού χώρου και του γαλαξία μας, μέχρι να
φτάσουν στη Γη.
α) Η Τοπική Ομάδα Γαλαξιών έχει διαστάσεις της τάξης του Mpc, ενώ
το διαγαλαξιακό μαγνητικό πεδίο έχει ένταση της τάξης του B = 10-7
G. ϒπολογίστε τον χρόνο ενεργειακών απωλειών σύγχροτρον E∕Ė για τα
ηλεκτρόνια ενέργειας Ee,max. Συγκρίνετέ τον με τον χρόνο διέλευσης από την
Τοπική Ομάδα, θεωρώντας σε πρώτη προσέγγιση ότι η κίνηση των ηλεκτρονίων
είναι ευθύγραμμη.
β) Ο Γαλαξίας μας έχει διαστάσεις της τάξης του kpc, ενώ το γαλαξιακό
μαγνητικό πεδίο έχει ένταση της τάξης του B = 3×10-6 G. Επαναλάβετε τους
προηγούμενους υπολογισμούς.
γ) Επαναλάβετε τους υπολογισμούς των ερωτημάτων (α) και (β) για πρωτόνια
ίδιας ενέργειας. Τι συμπεράσματα βγάζετε;
΄Ενας ραδιοαστρονόμος παρατηρεί μια αστροφυσική πηγή που θεωρείται ότι εκπέμπει ακτινοβολία σύγχροτρον. Η λαμπρότητα της πηγής φθίνει σε κλίμακα χρόνου ενός μήνα. Τό φάσμα της παρουσιάζει κορυφή σε μια χαρακτηριστική συχνότητα, 1 GHz. ϒπολογίστε το μαγνητικό πεδίο αυτής και την ενέργεια των ηλεκτρονίων που ακτινοβολούν.
Μια αστροφυσική πηγή παρουσιάζει φάσμα της μορφής νόμου δύναμης με εκθέτη α και μεταξύ των ενεργειών ϵmin και ϵmax. Αν η ακτινοβολία αυτή παράγεται από σχετικιστικά ηλεκτρόνια που εκπέμπουν σύγχροτρον ακτινοβολία, τότε αυτά θα είναι της μορφής:
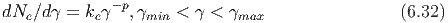
Δίνονται: R = 1015 cm, L = 1038 erg/sec, p = 4, ϵ min = 1019 keV, ϵ max = 1028 keV.
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press
(3rd edition).
Blumenthal, G. B., & Gould, R. J. (1970). “Bremsstrahlung, Synchrotron
Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute
Gases”. Reviews of Modern Physics, 42, 237.
Rybicki, B. G. & Lightman, P. A., (1985), Radiative Processes in Astrophysics.
Wiley.
Οι διαδικασίες υψηλών ενεργειών που περιγράφηκαν στα προηγούμενα κεφάλαια, καθώς και η επιτάχυνση σωματιδίων σε υψηλές ενέργειες η οποία θα περιγραφεί στο επόμενο κεφάλαιο, λαμβάνουν χώρα στο εσωτερικό αστροφυσικών πλασμάτων και γενικά επηρεάζονται από τις ιδιότητές τους. Στο παρόν κεφάλαιο θα γίνει μία σύντομη παρουσίαση των στοιχείων που θα χρειαστούν στη μελέτη επιτάχυνσης σωματιδίων (επόμενο κεφάλαιο), εστιάζοντας στη μελέτη ωστικών κυμάτων. Στο κεφάλαιο 9 θα γίνει λεπτομερέστερη μελέτη των ροών πλάσματος· στην παρούσα μελέτη θα αγνοήσουμε αρχικά το μαγνητικό πεδίο και θα μελετήσουμε ωστικά κύματα σε μη σχετικιστικά, υδροδυναμικά, συμπιεστά ρευστά, δηλ. σε αέρια. Αρχικά θα παρουσιάσουμε τις βασικές εξισώσεις της υδροδυναμικής που αντιστοιχούν στη διατήρηση μάζας, ενέργειας και ορμής, και στη συνέχεια τις συνθήκες άλματος στα ωστικά κύματα.
΄Εστω ένας σταθερός όγκος δτ στον χώρο. Ο ρυθμός ελάττωσης της μάζας που
βρίσκεται μέσα στον όγκο αυτό είναι -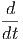 ∭
ρ dτ = -∭
∭
ρ dτ = -∭
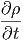 dτ, επομένως σε
χρόνο dt η μάζα ελαττώνεται κατά -∭
dτ, επομένως σε
χρόνο dt η μάζα ελαττώνεται κατά -∭
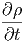 dτ dt.
dτ dt.
Λόγω διατήρησης μάζας, ίση μάζα περνά στον χρόνο dt την επιφάνεια δS που
περικλείει τον όγκο. Από μια στοιχειώδη επιφάνεια dS σε χρόνο dt περνά μάζα
ρV ⊥dt dS = ρV ⋅ dS dt. Το γινόμενο ρV εκφράζει τη ροή μάζας (μάζα ανά
επιφάνεια, ανά χρόνο). Η συνολική μάζα που περνά την επιφάνεια δS είναι
∯
ρV ⋅dS dt = ∭
∇⋅ (ρV )dτ dt χρησιμοποιώντας το θεώρημα της απόκλισης.
Εξισώνοντας τις δυο εκφράσεις έχουμε ∭
![[ ]
∂ρ
---+ ∇ ⋅ (ρV )
∂t](HEA_files/HEA182x.png) dτ = 0. Επιλέγοντας
τον όγκο δτ αρκούντως μικρό ώστε η ολοκληρωτέα να είναι σταθερή προκύπτει
τελικά
dτ = 0. Επιλέγοντας
τον όγκο δτ αρκούντως μικρό ώστε η ολοκληρωτέα να είναι σταθερή προκύπτει
τελικά
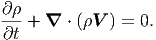 | (7.1) |
΄Ομοια θα βρούμε το ισοζύγιο της ορμής, λαμβάνοντας υπόψη τις προσθαφαιρέσεις
λόγω των δυνάμεων και των κινήσεων του αερίου.
Θα βρούμε την εξίσωση που εκφράζει τη διατήρηση της 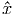 ορμής και μετά θα
γενικεύσουμε το αποτέλεσμα.
ορμής και μετά θα
γενικεύσουμε το αποτέλεσμα.
Ο ρυθμός αύξησης της 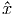 ορμής μέσα στον τυχαίο σταθερό όγκο δτ είναι
ορμής μέσα στον τυχαίο σταθερό όγκο δτ είναι
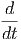 ∭
ρV xdτ = ∭
∭
ρV xdτ = ∭
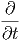 (ρV x)dτ.
(ρV x)dτ.
Από το μέρος dS της επιφάνειας που περικλείει τον όγκο, λόγω μακροσκοπικής
κίνησης του ρευστού με ταχύτητα V εξέρχεται 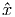 ορμή ανά χρόνο
ορμή ανά χρόνο
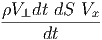 = ρV xV ⋅ dS. Η αντίστοιχη συνολική εξερχόμενη
= ρV xV ⋅ dS. Η αντίστοιχη συνολική εξερχόμενη 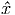 ορμή ανά χρόνο
είναι ∯
ρV xV ⋅ dS = ∭
∇⋅
ορμή ανά χρόνο
είναι ∯
ρV xV ⋅ dS = ∭
∇⋅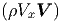 dτ χρησιμοποιώντας το θεώρημα της
απόκλισης.
dτ χρησιμοποιώντας το θεώρημα της
απόκλισης.
Λόγω της πίεσης το αέριο ασκεί δύναμη στο περιβάλλον του ∯
PdS = ∭
∇P dτ
η οποία αφαιρεί 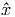 ορμή στη μονάδα του χρόνου ∭
ορμή στη μονάδα του χρόνου ∭
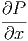 dτ.
dτ.
Αν υπάρχουν δυνάμεις όγκου f (δύναμη ανά όγκο) αυτές προσθέτουν 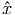 ορμή
στη μονάδα του χρόνου ∭
fxdτ, όπου fx = f ⋅
ορμή
στη μονάδα του χρόνου ∭
fxdτ, όπου fx = f ⋅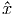 .
.
Το ισοζύγιο της 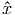 ορμής είναι λοιπόν ∭
ορμής είναι λοιπόν ∭
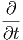 (ρV x)dτ = ∭
fxdτ-∭
(ρV x)dτ = ∭
fxdτ-∭
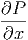 dτ-∭
∇⋅
dτ-∭
∇⋅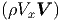 dτ
ή ισοδύναμα
dτ
ή ισοδύναμα 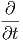 (ρV x) + ∇⋅
(ρV x) + ∇⋅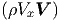 +
+ 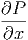 = fx. Γενικεύοντας το αποτέλεσμα και
για τις άλλες δύο συνιστώσες της ορμής μπορούμε να γράψουμε
= fx. Γενικεύοντας το αποτέλεσμα και
για τις άλλες δύο συνιστώσες της ορμής μπορούμε να γράψουμε
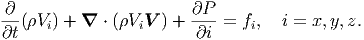 | (7.2) |
Χρησιμοποιώντας την εξίσωση (7.1) μπορούμε να γράψουμε την εξίσωση ορμής σαν
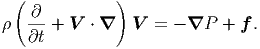 | (7.3) |
΄Ομοια θα εκφράσουμε τη διατήρηση ενέργειας. Η ενέργεια του αερίου που σε κάθε
στιγμή βρίσκεται μέσα στον σταθερό όγκο δτ είναι το άθροισμα της κινητικής
ενέργειας λόγω της μακροσκοπικής κίνησης με ταχύτητα V και της εσωτερικής
ενέργειας λόγω των θερμικών κινήσεων ∭
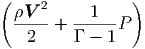 dτ, όπου Γ ο
πολυτροπικός δείκτης του αερίου· για μονατομικό αέριο Γ = 5∕3. Ο ρυθμός
μεταβολής της ενέργειας αυτής είναι ∭
dτ, όπου Γ ο
πολυτροπικός δείκτης του αερίου· για μονατομικό αέριο Γ = 5∕3. Ο ρυθμός
μεταβολής της ενέργειας αυτής είναι ∭
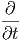
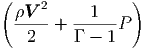 dτ, επομένως η
ενέργεια αυξάνεται κατά ∭
dτ, επομένως η
ενέργεια αυξάνεται κατά ∭
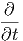
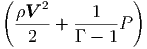 dτ dt σε χρόνο dt.
dτ dt σε χρόνο dt.
Για να γράψουμε την έκφραση της διατήρησης ενέργειας πρέπει να λάβουμε υπόψη
κάθε ενέργεια που προστίθεται ή αφαιρείται από το αέριο που βρίσκεται στον
συγκεκριμένο όγκο.
Αν υπάρχει θέρμανση που προσθέτει ενέργεια q ανά μονάδα μάζας και ανά
μονάδα χρόνου τότε στον χρόνο dt προστίθεται ενέργεια ∭
ρq dτ dt.
Αν ασκείται εξωτερική δύναμη f ανά όγκο του αερίου τότε μέσω του έργου της σε
χρόνο dt προσθέτει ενέργεια ∭
dτ f ⋅V dt.
Λόγω του έργου της δύναμης πίεσης που ασκείται μεταξύ αερίου και περιβάλλοντος
στην επιφάνεια που περικλείει τον συγκεκριμένο όγκο, αφαιρείται ενέργεια
∯
dS P ⋅V dt.
Τέλος, λόγω της κίνησης του αερίου που έχει ως αποτέλεσμα από το μέρος dS της
επιφάνειας σε χρόνο dt να εξέρχεται όγκος V ⊥dt dS = V ⋅ dS dt αφαιρείται
ενέργεια ∯
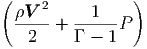 V ⋅ dS dt.
V ⋅ dS dt.
Προσθέτοντας τις δύο τελευταίες συνεισφορές, η ενέργεια που αφαιρείται από την
επιφάνεια που περικλείει τον όγκο είναι ∯
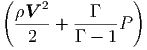 V ⋅ dS dt.
V ⋅ dS dt.
(΄Ολες οι προηγούμενες εκφράσεις είναι αλγεβρικές, δηλ. αρνητικό πρόσημο σημαίνει
αντίθετη συνεισφορά στο ενεργειακό ισοζύγιο.)
Η διατήρηση ενέργειας γράφεται λοιπόν
∭
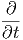
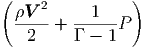 dτ dt = ∭
ρq dτ dt+∭
ρf⋅V dt dτ-∯
dτ dt = ∭
ρq dτ dt+∭
ρf⋅V dt dτ-∯
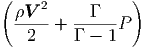 V ⋅dS dt,
ή χρησιμοποιώντας το θεώρημα της απόκλισης
V ⋅dS dt,
ή χρησιμοποιώντας το θεώρημα της απόκλισης
∭
![[ ∂ ( ρV 2 ) ( ρV 2 Γ ) ]
--- -----+ ρe + ∇ ⋅ -----V + -----P V - f ⋅ V - ρq
∂t 2 2 Γ - 1](HEA_files/HEA215x.png) dτ = 0.
dτ = 0.
Επιλέγοντας τον όγκο δτ αρκούντως μικρό ώστε η ολοκληρωτέα να είναι σταθερή
προκύπτει τελικά
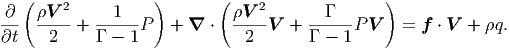 | (7.4) |
Γενικά οι ροές αερίων δεν είναι πάντα ομαλές. Σε ορισμένες περιπτώσεις είναι αναπόφευκτη η δημιουργία ασυνεχειών, μέσα στις οποίες το αέριο δεν βρίσκεται σε θερμοδυναμική ισορροπία. ΄Οπως θα δούμε στη συνέχεια αυτό συμβαίνει όταν τα αέρια κινούνται με υπερηχητικές ταχύτητες.
΄Ενα παράδειγμα για τη δημιουργία ασυνέχειας είναι το ακόλουθο: ΄Εστω ότι έχουμε ένα κυλινδρικό δοχείο μεγάλου μήκους γεμάτο με ιδανικό μονατομικό αέριο, το οποίο είναι κλειστό στη μια μεριά με ένα κινούμενο έμβολο. ΄Εστω ότι για t = 0 αρχίζουμε να κινούμε το έμβολο με σταθερή ταχύτητα V ε. Προφανώς τα άτομα/μόρια που βρίσκονται κοντά στην επιφάνεια του εμβόλου εξαναγκάζονται να κινηθούν με ταχύτητα V ε και αρχικά δημιουργείται ένα πύκνωμα και μια αύξηση πίεσης (να σημειώσουμε εδώ ότι η μέση ταχύτητα της ροής είναι ανεξάρτητη από τις θερμικές κινήσεις μέτρο των οποίων είναι η θερμοκρασία). Η πληροφορία ότι η πίεση αυξήθηκε, η οποία θα οδηγήσει σε κίνηση τελικά όλα τα άτομα/μόρια του δοχείου, διαδίδεται με πεπερασμένη ταχύτητα, την ταχύτητα του ήχου Cs. Για μικρές ταχύτητες του εμβόλου V ε < Cs υπάρχει αρκετός χρόνος να διαδοθεί η πληροφορία και να αποκατασταθεί η ισορροπία. Τα τελευταία άτομα/μόρια που «μαθαίνουν τα νέα» τη χρονική στιγμή t βρίσκονται σε απόσταση (Cs - V ε)t από το έμβολο. Τι γίνεται όμως αν κινήσουμε το έμβολο με ταχύτητα V ε > Cs; Τότε δεν δίνουμε χρόνο στα άτομα/μόρια να αντιδράσουν και να μεταδώσουν την πληροφορία ομαλά, αφού τα ηχητικά κύματα είναι πιο αργά από το έμβολο. Σίγουρα βέβαια κοντά στο έμβολο τα άτομα/μόρια έχουν ταχύτητα V ε όπως πριν, ενώ σε κάποια απόσταση το αέριο παραμένει ακίνητο. Το αέριο λύνει το πρόβλημα «επικοινωνίας» αυξάνοντας την ταχύτητα του ήχου σε μια περιοχή κοντά στο έμβολο, κάτι που συνεπάγεται αύξηση της θερμοκρασίας, της πίεσης και της πυκνότητας. Το μέτωπο αυτής της πυκνής περιοχής είναι το ωστικό κύμα. Το έμβολο σπρώχνει βίαια το αέριο όπως ένα εκχιονιστικό μηχάνημα σπρώχνει και συσσωρεύει μπροστά του το χιόνι. Και στις δύο περιπτώσεις δημιουργείται μια ασυνέχεια στη ροή (το άκρο αυτής της περιοχής βρίσκεται εκεί όπου τελειώνει η περιοχή μεγάλης πίεσης), η οποία κινείται με ταχύτητα V s, μεγαλύτερη από την ταχύτητα του εμβόλου ή του εκχιονιστικού μηχανήματος.
Η δημιουργία της ασυνέχειας είναι συνέπεια του γεγονότος ότι η αδιαβατική
ταχύτητα του ήχου με την οποία μεταφέρεται η πληροφορία μέσα σε ένα αέριο είναι
ανάλογη της θερμοκρασίας, πυκνότητας και πίεσης. Συγκεκριμένα είναι
Cs = 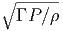 ∝ T1∕2 ∝ ρ(Γ-1)∕2 ∝ P(Γ-1)∕2Γ, διότι στις αδιαβατικές μεταβολές
(σταθερής) μάζας ΔM του αερίου, η οποία καταλαμβάνει (μεταβλητό) όγκο
Δτ = ΔM∕ρ είναι P(Δτ)Γ = σταθερό, ή P ∝ ρΓ. Κατά συνέπεια, όταν
δημιουργείται μια μεταβολή μέσα στο αέριο, το μέτωπο των πυκνότερων τμημάτων
του κινείται πιο γρήγορα και τείνει να προσπεράσει το μέτωπο των πιο αραιών
τμημάτων. Η προσπέραση είναι βέβαια αδύνατη, αλλά η προηγούμενη σκέψη δείχνει
ότι η απόσταση μεταξύ πυκνών και αραιών τμημάτων ολοένα και μικραίνει, δηλ. η
κλίση των μεγεθών ολοένα και μεγαλώνει. ΄Οταν η απόσταση αυτή γίνει μηδενική, η
κλίση γίνεται άπειρη και έχει δημιουργηθεί ασυνέχεια, όπως φαίνεται στο σχήμα 7.1
(πρακτικά η ασυνέχεια έχει πάχος συγκρίσιμο με τη μέση ελεύθερη διαδρομή, η
οποία είναι όμως πολύ μικρή σε σχέση με τις διαστάσεις που μας ενδιαφέρουν).
∝ T1∕2 ∝ ρ(Γ-1)∕2 ∝ P(Γ-1)∕2Γ, διότι στις αδιαβατικές μεταβολές
(σταθερής) μάζας ΔM του αερίου, η οποία καταλαμβάνει (μεταβλητό) όγκο
Δτ = ΔM∕ρ είναι P(Δτ)Γ = σταθερό, ή P ∝ ρΓ. Κατά συνέπεια, όταν
δημιουργείται μια μεταβολή μέσα στο αέριο, το μέτωπο των πυκνότερων τμημάτων
του κινείται πιο γρήγορα και τείνει να προσπεράσει το μέτωπο των πιο αραιών
τμημάτων. Η προσπέραση είναι βέβαια αδύνατη, αλλά η προηγούμενη σκέψη δείχνει
ότι η απόσταση μεταξύ πυκνών και αραιών τμημάτων ολοένα και μικραίνει, δηλ. η
κλίση των μεγεθών ολοένα και μεγαλώνει. ΄Οταν η απόσταση αυτή γίνει μηδενική, η
κλίση γίνεται άπειρη και έχει δημιουργηθεί ασυνέχεια, όπως φαίνεται στο σχήμα 7.1
(πρακτικά η ασυνέχεια έχει πάχος συγκρίσιμο με τη μέση ελεύθερη διαδρομή, η
οποία είναι όμως πολύ μικρή σε σχέση με τις διαστάσεις που μας ενδιαφέρουν).
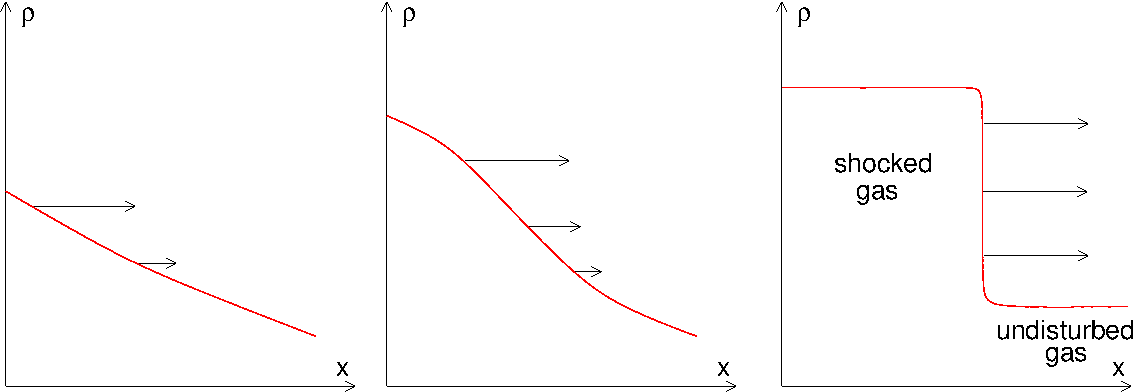
Στο εσωτερικό της ασυνέχειας δεν είναι εύκολο να περιγράψουμε το αέριο (το
οποίο υπόκειται σε μη-αντιστρεπτή μεταβολή καθώς περνάει την ασυνέχεια).
΄Ομως, μπορούμε να παρακάμψουμε τη δυσκολία αυτή και να συνδέσουμε
τις δύο καταστάσεις πριν και μετά την ασυνέχεια μέσω νόμων διατήρησης.
Χωρίς βλάβη της γενικότητας μπορούμε να θεωρήσουμε ως επίπεδο της ασυνέχειας
το x = 0 (τοπικά η ασυνέχεια είναι πάντα επίπεδη), δηλ. είναι προτιμότερο να
εργαστούμε στο σύστημα αναφοράς στο οποίο η ασυνέχεια είναι ακίνητη και να
επιλέξουμε τον άξονα x κάθετα στο επίπεδο της ασυνέχειας. ΄Εστω το μέρος «2»
είναι το μέρος x > 0 του αερίου απ΄ όπου έχει περάσει η ασυνέχεια (δηλ. το
πυκνότερο μέρος στο οποίο η ταχύτητα του ήχου έχει αυξηθεί) με πυκνότητα ρ2,
πίεση P2 και ταχύτητα V 2 (ως προς την ασυνέχεια), ενώ το μέρος «1» είναι το μέρος
x < 0 που δεν έχει περάσει, με πυκνότητα ρ1, πίεση P1 και ταχύτητα V 1 (ως προς
την ασυνέχεια).
Ολοκληρώνοντας την εξίσωση (7.1) ως προς x σε ένα απειροστό διάστημα που
περιλαμβάνει την ασυνέχεια, δηλ. σε διάστημα (-ϵ,ϵ) με ϵ → 0+, έχουμε
lim ϵ→0+ ∫
-ϵϵ![[ ]
∂ ρ ∂(ρVx ) ∂(ρVy) ∂ (ρVz )
∂t-+ --∂x---+ --∂y---+ --∂z---](HEA_files/HEA218x.png) dx = 0 ⇔ lim ϵ→0+
dx = 0 ⇔ lim ϵ→0+![[ρVx ]](HEA_files/HEA219x.png) -ϵϵ = 0,
διότι όλοι οι όροι είναι ομαλοί (και άρα το ολοκλήρωμά τους μηδενικό),
εκτός της παραγώγου ως προς x που είναι άπειρη λόγω της ασυνέχειας.
΄Ετσι βρίσκουμε την πρώτη συνθήκη άλματος που εκφράζει τη διατήρησης
μάζας
-ϵϵ = 0,
διότι όλοι οι όροι είναι ομαλοί (και άρα το ολοκλήρωμά τους μηδενικό),
εκτός της παραγώγου ως προς x που είναι άπειρη λόγω της ασυνέχειας.
΄Ετσι βρίσκουμε την πρώτη συνθήκη άλματος που εκφράζει τη διατήρησης
μάζας
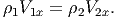 | (7.5) |
΄Ομοια το ολοκλήρωμα της εξίσωσης (7.2) δίνει ρ1V 1x2 + P
1 = ρ2V 2x2 + P
2 για
i = x, ρ1V 1xV 1y = ρ2V 2xV 2y για i = y και ρ1V 1xV 1z = ρ2V 2xV 2z για i = z, με τις
δύο τελευταίες να απλοποιούνται σε V 1y = V 2y και V 1z = V 2z λόγω της
συνθήκης (7.5). ΄Ετσι, οι συνθήκες άλματος που εκφράζουν τη διατήρηση της ορμής
κάθετα και παράλληλα στο επίπεδο της ασυνέχειας (δηλ. στη διεύθυνση 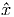 και στο
επίπεδο yz) γράφονται:
και στο
επίπεδο yz) γράφονται:
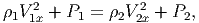 | (7.6) |
 | (7.7) |
Το ολοκλήρωμα της εξίσωσης (7.4) δίνει όμοια 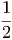 ρ1V 12V
1x+
ρ1V 12V
1x+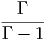 P1V 1x =
P1V 1x = 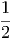 ρ2V 22V
2x+
ρ2V 22V
2x+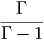 P2V 2x.
Χρησιμοποιώντας τις συνθήκες (7.5) και (7.7) η συνθήκη άλματος που εκφράζει τη
διατήρηση ενέργειας γράφεται:
P2V 2x.
Χρησιμοποιώντας τις συνθήκες (7.5) και (7.7) η συνθήκη άλματος που εκφράζει τη
διατήρηση ενέργειας γράφεται:
 | (7.8) |
Οι πέντε συνθήκες άλματος (7.5)–(7.8) καθορίζουν μονοσήμαντα την κατάσταση στο μέρος «2» αν γνωρίζουμε αυτή του μέρους «1» και αντίστροφα.
Μπορεί να αποδειχθεί ότι συνεπάγονται
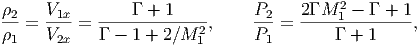 | (7.9) |
όπου M1 είναι ο αριθμός Mach του μέρους «1»
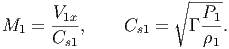 | (7.10) |
Η πρώτη από τις εξισώσεις (7.9) συνεπάγεται ότι ρ2 > ρ1 ⇔ M1 > 1. Η ίδια σχέση, εναλλάσσοντας τους δείκτες 1 και 2 δίνει ότι ρ1 < ρ2 ⇔ M2 < 1. ΄Αρα σε ένα ωστικό κύμα έχουμε πάντα μετάβαση από υπερηχητική σε υποηχητική ροή. Πάντα αναφερόμαστε στις συνιστώσες της ταχύτητας κάθετα στο επίπεδο της ασυνέχειας και στο σύστημα όπου η ασυνέχεια είναι ακίνητη.
Στο όριο που η ταχύτητα του μέρους «1» είναι κατά πολύ μεγαλύτερη της
ταχύτητας ήχου στο ίδιο μέρος, δηλ. M1 » 1, λέμε ότι έχουμε ισχυρή ασυνέχεια,
διότι ο λόγος συμπίεσης γίνεται μέγιστος και ίσος με 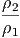 =
= 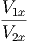 =
= 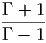 . Στην
περίπτωση που Γ = 5∕3 αυτός ο λόγος ισούται με 4, δηλ. ρ2 = 4ρ1 και
V 1x = 4V 2x.
. Στην
περίπτωση που Γ = 5∕3 αυτός ο λόγος ισούται με 4, δηλ. ρ2 = 4ρ1 και
V 1x = 4V 2x.
Τα αποτελέσματα γενικά τροποποιούνται με την ύπαρξη μαγνητικού πεδίου.
Αναφέρουμε δύο οριακές περιπτώσεις:
Αν το μαγνητικό πεδίο είναι κάθετο στο επίπεδο της ασυνέχειας τόσο οι συνθήκες
άλματος (7.5)–(7.8) όσο και οι σχέσεις (7.9) δεν αλλάζουν (απλά σε αυτές
προστίθεται η συνθήκη B1x = B2x σαν αποτέλεσμα της διατήρησης μαγνητικής ροής,
∇ ⋅B = 0).
Αν το μαγνητικό πεδίο είναι πάνω στο επίπεδο της ασυνέχειας, τότε αφενός στη
συνθήκη άλματος για τη διατήρηση ορμής η πίεση αντικαθίσταται από την ολική
πίεση P + 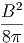 και αφετέρου στη συνθήκη άλματος για τη διατήρηση ενέργειας
προστίθεται η ροή Poynting
και αφετέρου στη συνθήκη άλματος για τη διατήρηση ενέργειας
προστίθεται η ροή Poynting 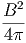 V x. Επίσης προστίθεται στις εξισώσεις η συνέχεια
της εφαπτομενικής συνιστώσας του ηλεκτρικού πεδίου E = -
V x. Επίσης προστίθεται στις εξισώσεις η συνέχεια
της εφαπτομενικής συνιστώσας του ηλεκτρικού πεδίου E = -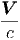 ×B, η οποία δίνει
ότι V 1xB1 = V 2xB2. Συνέπεια αυτών των αλλαγών είναι ο λόγος συμπίεσης να
δίνεται από τη σχέση
×B, η οποία δίνει
ότι V 1xB1 = V 2xB2. Συνέπεια αυτών των αλλαγών είναι ο λόγος συμπίεσης να
δίνεται από τη σχέση
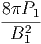 ο λόγος θερμικής προς μαγνητική πίεση στο μέρος «1».
ο λόγος θερμικής προς μαγνητική πίεση στο μέρος «1».
Στο παράδειγμα με το έμβολο που κινείται με υπερηχητική ταχύτητα V ε μέσα σε
ακίνητο μονατομικό αέριο, έστω η πυκνότητα και πίεση του αδιατάρακτου
αερίου είναι ρ1 και P1, αντίστοιχα. Η ταχύτητα του ήχου στο μέρος αυτό θα
είναι Cs1 = 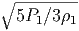 . Αν έχουμε ισχυρή ασυνέχεια V ε » Cs1 ο λόγος
συμπίεσης θα είναι 4. ΄Αρα η πυκνότητα στο μέρος του αερίου κοντά στο έμβολο
που έχει συμπιεστεί (από το οποίο έχει περάσει το ωστικό κύμα) θα είναι
ρ2 = 4ρ1 και η πίεση θα είναι P2 = (5∕4)M12P
1. Αν U είναι η ταχύτητα
της ασυνέχειας, τότε στο σύστημα της ασυνέχειας θα είναι V 1 = U και
V 2 = U - V ε, οπότε η σχέση V 1 = 4V 2 δίνει την ταχύτητα του ωστικού κύματος
U = (4∕3)V ε.
. Αν έχουμε ισχυρή ασυνέχεια V ε » Cs1 ο λόγος
συμπίεσης θα είναι 4. ΄Αρα η πυκνότητα στο μέρος του αερίου κοντά στο έμβολο
που έχει συμπιεστεί (από το οποίο έχει περάσει το ωστικό κύμα) θα είναι
ρ2 = 4ρ1 και η πίεση θα είναι P2 = (5∕4)M12P
1. Αν U είναι η ταχύτητα
της ασυνέχειας, τότε στο σύστημα της ασυνέχειας θα είναι V 1 = U και
V 2 = U - V ε, οπότε η σχέση V 1 = 4V 2 δίνει την ταχύτητα του ωστικού κύματος
U = (4∕3)V ε.
(α) Από τις συνθήκες μετάβασης σε ένα ισχυρό ωστικό κύμα δείξτε ότι ο
λόγος θερμοκρασιών είναι 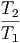 =
= 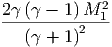 , όπου M12 =
, όπου M12 = 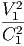 , C12 = γ
, C12 = γ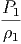 .
.
(β) ΄Ενα ωστικό κύμα υπερκαινοφανούς κινείται με ταχύτητα v1 = 500 km
s-1 μέσα στο (ακίνητο) μεσοαστρικό υλικό, του οποίου η ταχύτητα ήχου είναι
C1 = 10 km s-1. Ποια η ταχύτητα και η θερμοκρασία του μεσοαστρικού υλικού
από το οποίο έχει περάσει το ωστικό κύμα; Ελέγξτε αν η ροή σε αυτό το μέρος
του ωστικού κύματος είναι υποηχητική.
Το μεσοαστρικό υλικό μπορεί να θεωρηθεί ιδανικό μονατομικό αέριο
πρωτονίων-ηλεκτρονίων, με πίεση P = 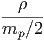 kBT.
kBT.
Δίνονται kB = 1.38 × 10-16, m
p = 1.67 × 10-24, στο σύστημα cgs.
Επίσης δίνονται οι σχέσεις: 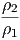 = r =
= r = 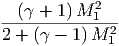 ,
, 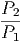 = 1 + γM12
= 1 + γM12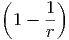 .
.
(α) Δείξτε τις συνθήκες άλματος για τις ασυνέχειες υδροδυναμικών ροών
![[ρVn ]](HEA_files/HEA249x.png) = 0,
= 0, ![2
[ρVn + P]](HEA_files/HEA250x.png) = 0,
= 0, ![[ρVnV t]](HEA_files/HEA251x.png) = 0,
= 0, ![[ 2 ]
ρV-- --γ---
2 Vn + γ - 1P Vn](HEA_files/HEA252x.png) = 0, όπου «n» οι
συνιστώσες κάθετα και «t» οι συνιστώσες πάνω στο επίπεδο της ασυνέχειας, ενώ η
αγκύλη συμβολίζει διαφορά των ποσοτήτων στο μέρος «1» και στο μέρος «2», δηλ.
= 0, όπου «n» οι
συνιστώσες κάθετα και «t» οι συνιστώσες πάνω στο επίπεδο της ασυνέχειας, ενώ η
αγκύλη συμβολίζει διαφορά των ποσοτήτων στο μέρος «1» και στο μέρος «2», δηλ.
![[...]](HEA_files/HEA253x.png) = (…)1 - (…)2.
= (…)1 - (…)2.
Αναφέρατε τι εκφράζει κάθε μια από αυτές.
(β) Με τη βοήθεια της 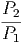 =
= 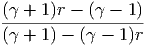 που προκύπτει από τις
συνθήκες άλματος και την
που προκύπτει από τις
συνθήκες άλματος και την ![[ρV 2+ P ]
n](HEA_files/HEA256x.png) = 0, δείξτε ότι r =
= 0, δείξτε ότι r = 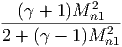 , όπου
r =
, όπου
r = 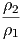 =
= 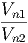 είναι ο λόγος συμπίεσης και Mn1 =
είναι ο λόγος συμπίεσης και Mn1 = 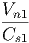 με Cs1 =
με Cs1 = 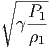 .
.
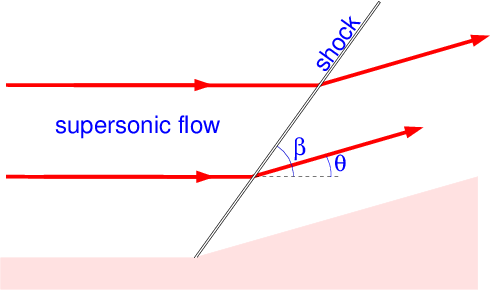
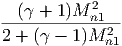 , βρείτε τη σχέση που
συνδέει τη γωνία β με τα θ και M1 = V 1∕Cs1.
, βρείτε τη σχέση που
συνδέει τη γωνία β με τα θ και M1 = V 1∕Cs1.
Ποιες οι συνθήκες άλματος για μια ασυνέχεια επαφής; Σε μια τέτοια περίπτωση δεν υπάρχει ροή κάθετα στην ασυνέχεια, απλά έχουμε δύο ρευστά σε επαφή.
΄Οπως έχει ήδη αναφερθεί οι διαδικασίες της Αστροφυσικής ϒψηλών Ενεργειών εμπλέκουν σωματίδια υψηλών ενεργειών. Την ύπαρξη τέτοιων σωματιδίων αντιλαμβανόμαστε είτε έμμεσα (οδηγούν στη δημιουργία παρατηρήσιμων φωτονίων υψηλής ενέργειας μέσω της ακτινοβολίας σύγχροτρον ή του αντίστροφου σκεδασμού Compton), είτε «άμεσα» μέσω της κοσμικής ακτινοβολίας (και στην περίπτωση αυτή ανιχνεύουμε φωτόνια υψηλών ενεργειών που δημιουργούνται από την αλληλεπίδραση της κοσμικής ακτινοβολίας με σωμάτια της ατμόσφαιρας). Το ερώτημα που θα μας απασχολήσει στο παρόν κεφάλαιο είναι πώς τα σωματίδια αυτά αποκτούν υψηλή ενέργεια, δηλ. πώς επιταχύνονται σε ενέργειες πολύ μεγαλύτερες από την ενέργεια ηρεμίας τους, E = γmc2 » mc2.
Ας εξετάσουμε τη δράση όλων των γνωστών δυνάμεων στο σωματίδιο:
Η ισχυρή πυρηνική δύναμη, λόγω της μικρής της εμβέλειας, θα χρειαζόταν να δώσει εξωπραγματικά υψηλή επιτάχυνση σε αποστάσεις της τάξης ~ 10-13cm. Το ίδιο ισχύει για την ασθενή πυρηνική δύναμη.
Θα μπορούσε η βαρύτητα να λύσει το πρόβλημα; Η βαρύτητα ως συντηρητική δύναμη που είναι, δεν μπορεί να δώσει υψηλές ταχύτητες μακρυά από τη βαρυτική πηγή που επιταχύνει το σωμάτιο. Αν σκεφτούμε κάποιο σωμάτιο να πλησιάζει κάποια βαρυτική πηγή, η κινητική του ενέργεια (γ - 1)mc2 αυξάνει. Καθώς όμως απομακρύνεται από την πηγή για να φτάσει σ΄ εμάς, η ενέργειά του μειώνεται και γίνεται όση ήταν και πριν πλησιάσει την πηγή. Η απάντηση λοιπόν είναι πάλι αρνητική.
Το τελικό συμπέρασμα αυτού του συλλογισμού, είναι ότι μόνο ηλεκτρομαγνητικές δυνάμεις μπορούν να επιταχύνουν σωμάτια σε μεγάλες ενέργειες.
Η ενέργεια που αποκτά ένα σωμάτιο εξαρτάται από το φορτίο του. Ας σκεφτούμε για παράδειγμα ένα πρωτόνιο, ένα νετρόνιο και ένα σωμάτιο άλφα να βρίσκονται μέσα σε ηλεκτρομαγνητικό πεδίο. Ποιο θα αποκτήσει μεγαλύτερη ενέργεια; Βέβαια το σωμάτιο άλφα, διότι έχει μεγαλύτερο φορτίο (ανεξάρτητα του γεγονότος ότι λόγω της μεγαλύτερης αδράνειάς του θα κινηθεί δυσκολότερα). Μικρότερη ενέργεια θα πάρει το πρωτόνιο και τελευταίο στη σειρά θα είναι το ουδέτερο νετρόνιο.
Ας σκεφτούμε ένα φορτίο να μπαίνει σε χώρο με στατικό (χρονοαμετάβλητο) μαγνητικό πεδίο και μηδενικό ηλεκτρικό πεδίο. Το φορτίο θα εκτελέσει ελικοειδή κίνηση στην οποία η ταχύτητά του αλλάζει διεύθυνση αλλά όχι μέτρο, άρα η ενέργεια παραμένει αμετάβλητη. Αν όμως το μαγνητικό πεδίο κινείται; Αφού η ενέργεια του φορτίου είναι σταθερή στο κινούμενο σύστημα, θα έχουμε μετατόπιση Doppler στο ακίνητο σύστημα αναφοράς. ΄Ετσι, «κινούμενα» μαγνητικά πεδία μπορούν να αυξήσουν την ενέργεια ενός φορτίου. Ακόμα κι αν στο κινούμενο σύστημα υπάρχει μόνο μαγνητικό πεδίο (και μηδενικό ηλεκτρικό), στο σύστημα του εργαστηρίου υπάρχει ηλεκτρικό πεδίο, στο οποίο ουσιαστικά οφείλεται η αύξηση στην ενέργεια του φορτίου. ΄Αλλος τρόπος να αυξήσουμε την ενέργεια ενός φορτίου είναι βέβαια η άμεση επιτάχυνση λόγω ηλεκτρικού πεδίου. ΄Ετσι κάποια πτώση δυναμικού ή σκέδαση Compton μπορεί να επιταχύνει φορτία.
Συνοψίζοντας, ο μόνος τρόπος να έχουμε φωτόνια υψηλής ενέργειας είναι αυτά να παράγονται χρησιμοποιώντας ενέργεια σωματιδίων, τα οποία με τη σειρά τους έχουν επιταχυνθεί είτε σε κινούμενα μαγνητικά πεδία είτε σε ηλεκτρικά πεδία.
Στη συνέχεια θα περιγράψουμε συγκεκριμένους μηχανισμούς επιτάχυνσης αυτού του τύπου με απώτερο σκοπό να προσπαθήσουμε να εξηγήσουμε το παρατηρούμενο φάσμα σωματιδίων υψηλής ενέργειας (π.χ. κοσμικών ακτίνων), το οποίο τυπικά είναι ένας νόμος δύναμης με εκθέτη 2–3 (εννοώντας ότι ο αριθμός σωματίων με ενέργειες από E ως E + dE είναι N(E)dE ∝ E-αdE, με α = 2 - 3). Τα φάσματα εκτείνονται σε πολύ μεγάλες ενέργειες· π.χ. κοσμικές ακτίνες έχουν παρατηρηθεί μέχρι 3 × 1020eV, όπως έχει ήδη αναφερθεί. Σ΄ αυτήν λοιπόν την περίπτωση έχουμε επιτάχυνση ενός μικρού κλάσματος σωματίων σε υπερ-υψηλές ενέργειες, ενώ περισσότερα σωματίδια έχουν μικρότερες ενέργειες. Ακόμα και στην περίπτωση που λαμβάνουμε ακτινοβολία υψηλών ενεργειών με φάσμα νόμο δύναμης, τα σωματίδια που την παράγουν μέσω επιτάχυνσης σε μαγνητικό πεδίο στην περίπτωση της ακτινοβολίας σύγχροτρον, ή μέσω αντίστροφου σκεδασμού Compton, πρέπει να έχουν ενεργειακό φάσμα νόμου δύναμης παραπλήσιο με αυτό των κοσμικών ακτίνων, όπως αποδείχθηκε στα κεφάλαια 5.3.4 και 6.3.
ϒπάρχουν επίσης ισχυρές ενδείξεις σε εκροές από ενεργούς γαλαξιακούς πυρήνες για κίνηση του συνόλου της εκροής – την οποία θα ονομάζουμε μακροσκοπική κίνηση σε αντιδιαστολή με την κίνηση μεμονωμένων σωματίων – με παράγοντα Lorentz μέχρι μερικές δεκάδες. Επίσης, το επικρατέστερο μοντέλο για την εξήγηση των εκλάμψεων γάμμα ακτινοβολίας απαιτεί επιτάχυνση του συνόλου της εκροής σε παράγοντα Lorentz μερικές εκατοντάδες. Τα δύο τελευταία παραδείγματα δείχνουν ότι κάποιες φορές όλη η ύλη σε κάποια περιοχή μπορεί να κινείται ισχυρά σχετικιστικά.
Το αντικείμενό μας είναι λοιπόν να εξηγήσουμε:
(α) φάσματα νόμου δύναμης και υπερ-υψηλές ενέργειες για μικρό κλάσμα σωματίων, και
(β) σχετικιστική μακροσκοπική κίνηση.
Στο υπόλοιπο του κεφαλαίου θα ασχοληθούμε με το πρώτο· το δεύτερο θέμα θα μας απασχολήσει σε επόμενο κεφάλαιο.
Ο μηχανισμός αυτός προτάθηκε από τον Fermi (1949). Πρώτα θα τον περιγράψουμε αφαιρετικά (μόνο την ιδέα σαν πρόβλημα Κλασικής Μηχανικής) και στη συνέχεια θα δούμε πού μπορεί να συναντάται σε Αστροφυσικά συστήματα.
΄Εστω ότι ένα σωμάτιο μάζας m κινείται σε χώρο όπου υπάρχουν διάσπαρτα κατανεμημένα κινούμενα σώματα (θα τα αποκαλούμε «νέφη», μεγάλης μάζας και μικρής ταχύτητας σε σχέση με τη μάζα και την ταχύτητα του σωματίου, τα οποία ανακλούν ελαστικά το σωμάτιο. Αν αυτά τα νέφη κινούνται με ταχύτητα V s και το σωμάτιο κινείται με ταχύτητα V , μετά από κάθε κρούση το σωμάτιο κερδίζει ή χάνει ενέργεια ανάλογα με το αν τα σώματα πριν την κρούση κινούνται σε αντίθετη ή στην ίδια κατεύθυνση.
Ας εξετάσουμε πρώτα το μη σχετικιστικό ισοδύναμο. Στο σύστημα αναφοράς του νέφους το σωμάτιο φαίνεται να πλησιάζει με ταχύτητα (V ∥ -V s) + V ⊥ (βλ. σχήμα 8.1). Μετά την κρούση η ταχύτητα στο σύστημα του νέφους θα είναι -(V ∥-V s) + V ⊥. ΄Αρα, στο αρχικό σύστημα αναφοράς V ′′ = -V ∥ + 2V s + V ⊥. Η μεταβολή της κινητικής ενέργειας είναι 2m(V s2 - V ⋅ V s), δηλ. κέρδος 2mV s(V ∥ + V s) στην περίπτωση μετωπικής κρούσης V ⋅ V s < 0, και ζημία 2mV s(V ∥ - V s) στην περίπτωση ακόλουθης κρούσης V ⋅V s > 0.
Στη σχετικιστική περίπτωση ο συλλογισμός είναι ο ίδιος· πρέπει όμως να χρησιμοποιήσουμε μετασχηματισμούς Lorentz όταν σκεφτόμαστε τη σχέση μεταξύ ταχυτήτων και ενεργειών από το ένα σύστημα στο άλλο. Το τελικό αποτέλεσμα είναι:
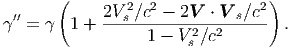 | (8.1) |
Αναπτύσσοντας κατά Taylor την εξίσωση 8.1 ως προς V s∕c και κρατώντας μέχρι δεύτερης τάξης όρους, έχουμε για το κέρδος ενέργειας (V ⋅V s < 0 για μετωπική κρούση)
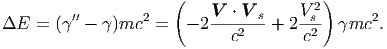 | (8.2) |
Για να υπολογίσουμε έναν στατιστικό μέσο όρο του ΔE θα πρέπει να λάβουμε υπόψη ότι η πιθανότητα για μετωπική κρούση είναι μεγαλύτερη από την πιθανότητα για ακόλουθη κρούση. Αυτό γίνεται εύκολα κατανοητό αν σκεφτούμε τη μονοδιάστατη περίπτωση. ΄Εστω ότι οδηγούμε ένα αυτοκίνητο με ταχύτητα V και στον δρόμο υπάρχουν και άλλα αυτοκίνητα που κινούνται με ταχύτητα μέτρου V s < V , κάποια στο ίδιο ρεύμα με εμάς και κάποια στο αντίθετο (με ίδιες πυκνότητες). Σε κάποιο χρονικό διάστημα Δt θα περάσουν δίπλα μας όχι μόνο όσα αυτοκίνητα βρίσκονται αρχικά σε απόσταση < V Δt μπροστά μας, αλλά και κάποια άλλα τα οποία μας πλησιάζουν και θα αποκτήσουν απόσταση < V Δt μέσα στον χρόνο Δt. Τα αυτοκίνητα που κινούνται με αντίρροπη ταχύτητα ως προς εμάς αντιστοιχούν στις μετωπικές κρούσεις. Αντίθετα, οι ακόλουθες κρούσεις θα είναι λιγότερες από τα αυτοκίνητα που βρίσκονται σε απόσταση V Δt, διότι πρέπει να αφαιρέσουμε αυτά που θα φύγουν από αυτήν την απόσταση στον χρόνο Δt. Η πιθανότητα η επόμενη κρούση να είναι μετωπική είναι ανάλογη του (V + V s)Δt, ενώ για ακόλουθη κρούση ανάλογη του (V - V s)Δt. Ο συντελεστής αναλογίας βρίσκεται από την κανονικοποίηση (το άθροισμα πιθανοτήτων είναι μονάδα) και έτσι βρίσκουμε τις πιθανότητες να είναι (V + V s)∕(2V ) και (V - V s)∕(2V ) για μετωπική και ακόλουθη κρούση, αντίστοιχα. ΄Αρα, η μέση αύξηση στην ενέργεια μετά από μια κρούση είναι
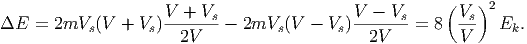 | (8.3) |
Ακριβείς υπολογισμοί στην τρισδιάστατη κίνηση και με σχετικιστικές ταχύτητες οδηγούν σε παρόμοιο αποτέλεσμα ΔE = (8∕3)(V s∕c)2E (εδώ E = γmc2 είναι η ολική ενέργεια του σωματίου, συμπεριλαμβανομένης της ενέργειας ηρεμίας mc2 και όχι μόνο η κινητική ενέργεια Ek = E - mc2 = (γ - 1)mc2 η οποία για μη-σχετικιστικές κινήσεις γίνεται mV 2∕2). Η αύξηση της ενέργειας εξαρτάται από το τετράγωνο του (V s∕c) και γι΄ αυτό ο μηχανισμός αυτός ονομάστηκε «δεύτερης τάξης». Να σημειώσουμε ότι ο μηχανισμός αυτός βασίζεται στην ιδιότητα μιας συλλογής από αλληλοσυγκρουόμενα σωμάτια να φτάσουν σε ισοκατανομή της ενέργειας.
Επειδή ο μέσος χρόνος μεταξύ των κρούσεων είναι < L∕V cos θ > ≈ 2L∕c, όπου L η μέση απόσταση μεταξύ νεφών, δηλ. προκύπτει σταθερός, και το μέσο κέρδος στην ενέργεια ΔE∕E επίσης σταθερό, οι συνεχείς κρούσεις θα οδηγήσουν στατιστικά σε εκθετική αύξηση της ενέργειας του σωματίου
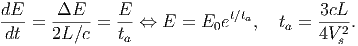 | (8.4) |
Ο χρόνος ta στον οποίο η ενέργεια αυξάνει σημαντικά είναι πολύ μεγαλύτερος του χρόνου μεταξύ των κρούσεων 2L∕c, δηλ. η αύξηση απαιτεί την υλοποίηση μεγάλου αριθμού κρούσεων.
Τα σωμάτια δεν μένουν για πάντα στην περιοχή των νεφών αλλά διαφεύγουν με κάποιο ρυθμό από αυτήν. ΄Εστω ότι ο μέσος χρόνος παραμονής (και επιτάχυνσης) είναι td. Τότε, το πλήθος των σωματίων που θα επιταχύνονται σε συνολικό χρονικό διάστημα από t ως t + dt, είναι N(t)dt ∝ e-t∕tddt. Αυτά τα σωμάτια όταν διαφύγουν θα έχουν ενέργεια E = E0et∕ta ⇔ t(E) = ln(E∕E 0)ta. Συνεπώς, τα σωμάτια που φεύγουν με ενέργειες από E ως E + dE είναι N(E)dE = N(t)dt ∝ E-1-ta∕tddE, δηλ. βρήκαμε νόμο δύναμης.
Ας σκεφτούμε τώρα την εφαρμογή αυτού του μηχανισμού. Η αρχική ιδέα του
Fermi ήταν πως τα «νέφη» είναι ανομοιογένειες μαγνητικού πεδίου (δηλ. έχουμε
κινούμενο μαγνητικό πεδίο) στον μεσοαστρικό χώρο, οι οποίες δρουν σαν
μαγνητικοί καθρέπτες για τα φορτισμένα σωμάτια, αναγκάζοντάς τα να ανακλώνται
ελαστικά. ΄Οπως ξέρουμε, ένα φορτισμένο σωμάτιο εκτελεί ελικοειδή τροχιά Larmor
μέσα σε ομογενές μαγνητικό πεδίο. Μπορούμε να χωρίσουμε την κίνηση σε
ευθύγραμμη και ομαλή με ορμή p∥ = γmV ∥ παράλληλα στο μαγνητικό πεδίο, και
ομαλή κυκλική με ορμή p⊥ = γmV ⊥ και ακτίνα r = p⊥∕qB κάθετα στο πεδίο. Αν το
πεδίο είναι ανομοιογενές τα p∥2 και p
⊥2 δεν διατηρούνται πια σταθερά, αν και το
άθροισμά τους είναι σταθερό (η δύναμη από μαγνητικό πεδίο είναι κάθετη
στην ταχύτητα και άρα δεν αλλάζει την ενέργεια E = 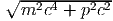 του
σωματίου αφού δεν παράγει έργο). Στην περίπτωση που το πεδίο αλλάζει λίγο
στην κλίμακα μήκους που καθορίζει η ακτίνα Larmor αποδεικνύεται (μέσω
λύσης της εξίσωσης Newton διαταράσσοντας την κίνηση γύρω από την
τροχιά Larmor) ότι η ποσότητα p⊥2∕B είναι «αδιαβατική αναλλοίωτη», δηλ.
μένει σταθερή κατά τη διάρκεια της κίνησης, κάτι που οδηγεί στο ακόλουθο
ενδιαφέρον συμπέρασμα: ΄Οταν το φορτίο κινείται προς μεγαλύτερες εντάσεις
πεδίου, η συνιστώσα p⊥ αυξάνει, οπότε η p∥ μειώνεται. Δηλ. το βήμα της
έλικας συνεχώς μικραίνει και για αρκούντως μεγάλες τιμές του B μπορεί να
μηδενιστεί. Στην περίπτωση αυτή το φορτίο ανακλάται σε έναν «μαγνητικό
καθρέπτη».
του
σωματίου αφού δεν παράγει έργο). Στην περίπτωση που το πεδίο αλλάζει λίγο
στην κλίμακα μήκους που καθορίζει η ακτίνα Larmor αποδεικνύεται (μέσω
λύσης της εξίσωσης Newton διαταράσσοντας την κίνηση γύρω από την
τροχιά Larmor) ότι η ποσότητα p⊥2∕B είναι «αδιαβατική αναλλοίωτη», δηλ.
μένει σταθερή κατά τη διάρκεια της κίνησης, κάτι που οδηγεί στο ακόλουθο
ενδιαφέρον συμπέρασμα: ΄Οταν το φορτίο κινείται προς μεγαλύτερες εντάσεις
πεδίου, η συνιστώσα p⊥ αυξάνει, οπότε η p∥ μειώνεται. Δηλ. το βήμα της
έλικας συνεχώς μικραίνει και για αρκούντως μεγάλες τιμές του B μπορεί να
μηδενιστεί. Στην περίπτωση αυτή το φορτίο ανακλάται σε έναν «μαγνητικό
καθρέπτη».
Παρότι ο μηχανισμός οδήγησε σε νόμο δύναμης παρουσιάζει διάφορα προβλήματα. Ο χρόνος που χρειάζεται για να φτάσει η ενέργεια ενός σωματίου σε επιθυμητά επίπεδα είναι αρκετά μεγάλος, κάτι που δεν δικαιολογεί να αμελήσουμε ενεργειακές απώλειες. Για παράδειγμα, έστω ότι V s∕c ~ 10-4 και L ~ 1pc. Ο χρόνος μεταξύ δυο κρούσεων είναι περίπου 2L∕c ~ 7 χρόνια, ενώ ο χρόνος που χρειάζεται το σωμάτιο για να επιταχυνθεί από κάποια ενέργεια σε e φορές μεγαλύτερη είναι ~ [(8∕3)(V s∕c)2]-1 φορές μεγαλύτερος, δηλ. κοντά ένα δισεκατομμύριο χρόνια! Φυσικά αν το πεδίο είναι εντονότερα ανομοιογενές, δηλ. το L είναι μικρότερο, ο χρόνος ελαττώνεται. Γενικά είναι
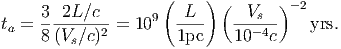
Ακόμα κι αν λύσουμε αυτό το πρόβλημα, είναι δύσκολο να απαντήσουμε μια άλλη ερώτηση: γιατί ο φασματικός δείκτης (-1 - ta∕td) έχει πάντα σχεδόν την ίδια τιμή; Με άλλα λόγια γιατί το td είναι συγκρίσιμο με το ta και συνδέεται με την ίδια σχέση με τα L και V s σε όλες τις κατανομές νεφών;
Βελτίωση του προηγούμενου μηχανισμού αποτελεί ο μηχανισμός Fermi πρώτης τάξης. Η ιδέα είναι απλή. ΄Οπως είδαμε στον μηχανισμό δεύτερης τάξης, το μέσο κέρδος σε ενέργεια είναι ανάλογο του (V s∕c)2, διότι οι μετωπικές κρούσεις μερικώς εξουδετερώνονται από τις ακόλουθες κρούσεις. Αν με κάποιο τρόπο εξασφαλίσουμε ότι μόνο μετωπικές κρούσεις είναι δυνατές, ο μηχανισμός θα γίνει πολύ αποδοτικότερος. Το κέρδος σε ενέργεια θα είναι, σύμφωνα με την εξίσωση (8.2), ΔE∕E = 2V V s∕c2, δηλ. ανάλογο του V s∕c. Για τον λόγο αυτό ο μηχανισμός ονομάστηκε «πρώτης τάξης».
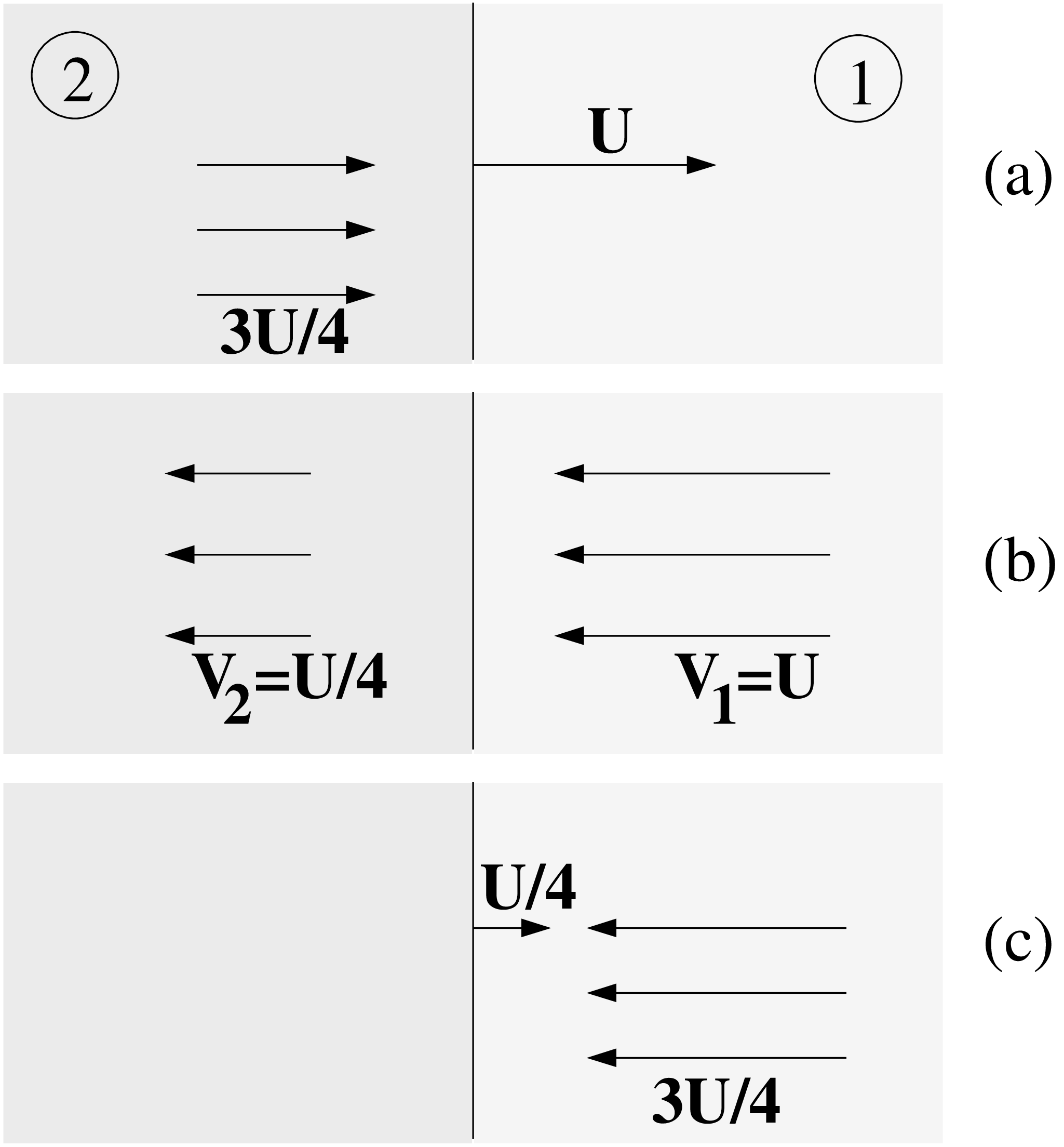
Το μηχανικό ανάλογο είναι ένα σωμάτιο να κινείται μεταξύ δύο νεφών τα οποία πλησιάζουν μεταξύ τους. Το ερώτημα είναι βέβαια πού μπορεί να υλοποιηθεί ένας τέτοιος μηχανισμός σε Αστροφυσικά συστήματα. Προξενεί εντύπωση ότι αυτό είναι ισοδύναμο με κινήσεις σωματίων που περνούν ασυνέχειες ροής πλάσματος, δηλ. στα ωστικά κύματα (shocks) που αναλύθηκαν στο προηγούμενο κεφάλαιο. Τέτοιες ασυνέχειες δημιουργούνται αυθόρμητα σε υπερηχητικές ροές, όπως σε αυτές που συνδέονται με εκρήξεις υπερκαινοφανών. Στην περίπτωση αυτή το υλικό που εκτοξεύεται έχει ταχύτητες ~ 104 km s-1, κατά πολύ μεγαλύτερες από τυπικές ταχύτητες ήχου του μεσοαστρικού υλικού που είναι το πολύ 10 km s-1. ΄Ετσι δημιουργείται μια ισχυρή ασυνέχεια, η οποία κινείται υπερηχητικά με ταχύτητα U, χωρίζοντας τον χώρο σε δυο μέρη: το μέρος «2» από το οποίο έχει περάσει η ασυνέχεια και το μέρος «1», βλ. σχήμα 8.2. ΄Ενα σωμάτιο που αρχικά βρίσκεται στο «1», βλέπει το μέρος «2» να κινείται προς το μέρος του με ταχύτητα 3U∕4 [βλ. σχήμα 8.2(a)]. Κατά συνέπεια η κρούση με το μέρος «2» θα είναι μετωπική και το σχετικό κέρδος ενέργειας του σωματίου θα είναι ΔE∕E = O(U∕c). Ακριβείς υπολογισμοί δείχνουν ότι το κέρδος είναι ΔE∕E = U∕2c. Μετά την κρούση το σωμάτιο βρίσκεται μέσα στο μέρος «2», όπου λόγω της τυρβώδους ροής αλλά και της ύπαρξης μαγνητικού πεδίου σκεδάζεται και αλλάζει κατεύθυνση κίνησης με τυχαίο τρόπο (χωρίς να αλλάζει ενέργεια), γιατί το μέσο είναι ισοτροπικό στο σύστημα ηρεμίας του. Στη συνέχεια, το σωμάτιο είτε θα διαφύγει από τη γειτονιά της ασυνέχειας είτε θα συγκρουστεί με το μέσο «1». Αν σκεφτούμε ότι η ροή σωματίων είναι το γινόμενο της αριθμητικής τους πυκνότητας με την ταχύτητα, η ροή σωματίων που απομακρύνεται από την ασυνέχεια και χάνεται στο μέσο «2» είναι n2(U∕4) [σχήμα 8.2(b)]. Πολύ κοντά στην ασυνέχεια και μέσα στο μέρος «2», τα μισά από τα σωμάτια απομακρύνονται και τα άλλα μισά ξαναπερνούν την ασυνέχεια. Αφού η μέση ταχύτητα αυτών των σωματίων είναι c∕2, η ροή σωματίων προς την ασυνέχεια είναι (n2∕2)(c∕2) = n2c∕4. Συμπέρασμα αυτού του συλλογισμού είναι ότι το κλάσμα των σωματίων που φεύγει μακρυά από την ασυνέχεια σε σχέση με αυτά που την ξαναπερνούν είναι μόλις U∕c! ΄Αρα η συντριπτική πλειοψηφία θα συγκρουστεί με το μέσο «1». ΄Οπως βλέπουμε από το σχήμα 8.2(c), πάλι η κρούση είναι μετωπική, οπότε το σωμάτιο θα ξανακερδίσει ενέργεια. Το φαινόμενο επαναλαμβάνεται και το σωμάτιο ποτέ δεν χάνει ενέργεια, σαν να συγκρούεται συνεχώς με δύο καθρέπτες που πλησιάζουν.
Μετά από δύο περάσματα από την ασυνέχεια (μπρος και πίσω, δηλ. ένας πλήρης κύκλος) είναι ΔE∕E = U∕2c + U∕2c = U∕c. ΄Αρα μετά από k κύκλους η ενέργεια θα είναι E = E0(1 + U∕c)k. Αφού η πιθανότητα να διαφύγει ένα σωμάτιο είναι U∕c, αν αρχικά είχαμε N0 σωμάτια, μετά από k κύκλους θα έχουμε N = N0(1 - U∕c)k. Απαλείφοντας το k έχουμε:
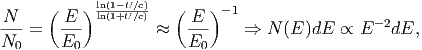 | (8.5) |
δηλ. ο εκθέτης στον νόμο δύναμης του ενεργειακού φάσματος είναι ακριβώς 2. Αν εξετάζουμε αέριο με Γ≠5∕3 τα αποτελέσματα θα αλλάξουν, οπότε ο εκθέτης δεν θα είναι ακριβώς 2, αλλά κοντά σ΄ αυτήν την τιμή. Το αποτέλεσμα αυτό υπήρξε ενθαρρυντικό για την εξήγηση της προέλευσης των κοσμικών ακτίνων με υποψήφια πηγή τις ασυνέχειες από εκρήξεις υπερκαινοφανών. ΄Ομως είναι δύσκολο να εξηγήσει την παραγωγή σωματίων με ενέργεια πάνω από ~ 1015eV. Ο λόγος είναι ότι η ασυνέχεια επιβραδύνεται καθώς σπρώχνει όλο και μεγαλύτερη μάζα μεσοαστρικού υλικού. Κάποιος άλλος λόγος λοιπόν πρέπει να υπάρχει και να εξηγεί την παραγωγή σωματίων υπερ-υψηλής ενέργειας.
Μια παραλλαγή της επιτάχυνσης σε ασυνέχειες είναι η περίπτωση ολίσθησης πάνω στην επιφάνεια ασυνέχειας η οποία κινείται κάθετα σε μαγνητικό πεδίο. Στο σχήμα 8.3 φαίνεται η γεωμετρία της περίπτωσης αυτής. ΄Ενα φορτίο q, μάζας m, βρίσκεται στο δεξιό μέρος του σχήματος, μέσα σε σταθερό μαγνητικό πεδίο B1 και ηλεκτρικό πεδίο E με E < B1. Η κίνηση του φορτίου, η οποία ικανοποιεί την εξίσωση d(γmv)∕dt = qE + q(v∕c) ×B, μπορεί να αναλυθεί σε μία ομαλή κυκλική γυροακτίνας rg = cp⊥∕|q|B και ταχύτητας v⊥, της οποίας το οδηγό κέντρο εκτελεί (1) ευθύγραμμη κίνηση με ταχύτητα v∥ στη διεύθυνση του μαγνητικού πεδίου, και (2) ολίσθηση «ηλεκτρικού πεδίου» με ταχύτητα
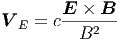 | (8.6) |
(αυτό διότι όπως μπορεί εύκολα να ελεγχθεί το ηλεκτρικό πεδίο μηδενίζεται στο σύστημα που κινείται με V E και άρα η κίνηση είναι Larmor στο σύστημα αυτό). ΄Ενας τρόπος να καταλάβουμε ποιοτικά τη φορά της V E είναι να σκεφτούμε ότι ένα θετικό φορτίο (το οποίο για τα πεδία του σχήματος περιστρέφεται με την ορθή φορά) λόγω της φοράς του ηλεκτρικού πεδίου έχει μεγαλύτερη ενέργεια στο πάνω μέρος της κίνησής του και άρα η τοπική ακτίνα Larmor είναι μεγαλύτερη στο πάνω μέρος της τροχιάς. Σε συνδυασμό με την ορθή φορά περιστροφής αυτό οδηγεί σε μετατόπιση της τροχιάς προς τα αριστερά. ΄Ομοια για ένα αρνητικό φορτίο η τοπική ακτίνα Larmor είναι μικρότερη στο πάνω μέρος της τροχιάς κάτι που σε συνδυασμό με την ανάδρομη περιστροφή οδηγεί ξανά σε μετατόπιση της τροχιάς προς τα αριστερά.
Η ταχύτητα V E είναι τέτοια που οδηγεί όλα τα φορτία προς την ασυνέχεια, βλ. σχήμα 8.3 (η V E είναι ανεξάρτητη του πρόσημου του φορτίου). ΄Οταν το σωμάτιο περάσει την ασυνέχεια μέρος της τροχιάς του θα βρεθεί στο αριστερό μέρος όπου το μαγνητικό πεδίο έχει μεγαλύτερη ένταση όπως συζητήθηκε στο προηγούμενο κεφάλαιο, ενώ το ηλεκτρικό μένει ίδιο. Συνεπώς η γυροακτίνα του σωματίου θα είναι μικρότερη (όπως και η ταχύτητα V E), οπότε το σωμάτιο ολισθαίνει πάνω στο επίπεδο της ασυνέχειας. Παρατηρούμε ότι η ολίσθηση είναι παράλληλη στο ηλεκτρικό πεδίο, οπότε το σωμάτιο κερδίζει ενέργεια. Το σχήμα 8.3 παριστάνει την κίνηση θετικού φορτίου· για αρνητικό φορτίο ο ίδιος συλλογισμός οδηγεί σε ολίσθηση προς διεύθυνση αντίθετη του E, οπότε έχουμε ξανά επιτάχυνση και κέρδος ενέργειας. Αυτή η ολίσθηση προέρχεται από την ανομοιογένεια του μαγνητικού πεδίου, και στη γενική περίπτωση είναι
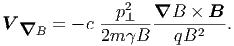 | (8.7) |
Δηλ. εκτός από την κυκλική κίνηση, την ομαλή κίνηση στη διεύθυνση του B, και την ολίσθηση λόγω της ύπαρξης ηλεκτρικού πεδίου, επιπρόσθετα υπάρχει μία δεύτερη ολίσθηση λόγω ανομοιογένειας του μέτρου του μαγνητικού πεδίου. (Παρατηρήστε ότι η V ∇B είναι αντίθετη για αντίθετα φορτία, οπότε δημιουργεί ρεύμα το οποίο τείνει να αναιρέσει το αίτιο που το προκάλεσε, δηλ. τη διαφορά του μαγνητικού πεδίου B2 - B1.)
Φορτία μέσα σε χώρο με ισχυρά ηλεκτρικά πεδία επιταχύνονται αν το δυναμικό στα διάφορα σημεία της τροχιάς τους μεταβάλλεται (ισοδύναμα αν η ταχύτητά τους έχει μη μηδενική προβολή πάνω στο ηλεκτρικό πεδίο). Πτώση δυναμικού V προκαλεί αύξηση ενέργειας qV σ΄ ένα θετικό φορτίο q (αντίστοιχα αύξηση δυναμικού επιταχύνει αρνητικό φορτίο). Αν έχουμε ηλεκτρικό πεδίο E, τότε το φορτίο κερδίζει ενέργεια qV ~ qEL όταν διανύει απόσταση L.
Πτώσεις δυναμικού συναντώνται οποτεδήποτε υπάρχει μαγνητικό πεδίο σε περιοχή περιστρεφόμενου αγωγού. Αφού τα φορτία του αγωγού είναι ευκίνητα (άπειρη αγωγιμότητα), ο νόμος του Ohm δίνει το ηλεκτρικό πεδίο στο εσωτερικό του αγωγού
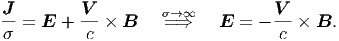 | (8.8) |
Η σχέση αυτή εκφράζει το γεγονός ότι το ηλεκτρικό πεδίο που οφείλεται σε
διαχωρισμό φορτίων εξουδετερώνει πλήρως το πεδίο που αναπτύσσεται εξ΄ επαγωγής
καθώς ο αγωγός κινείται μέσα στο μαγνητικό πεδίο. ΄Οπως θα δούμε και στο
επόμενο κεφάλαιο 9.2.2 εκφράζει ισοδύναμα ότι στο σύστημα που κινείται μαζί με
τον αγωγό το ηλεκτρικό πεδίο είναι μηδέν.
Αν ο χώρος έξω από τον αγωγό είναι σχεδόν κενός, το ηλεκτρικό πεδίο δεν
ακολουθεί τη σχέση (8.8) και άρα δεν είναι απαραίτητα κάθετο στο μαγνητικό πεδίο.
Αφού τα φορτία κινούνται κυρίως κατά μήκος των μαγνητικών γραμμών, η
συνιστώσα του E πάνω στο B τα επιταχύνει, ενώ η κάθετη συνιστώσα
καθορίζει τι είδους φορτία (θετικά ή αρνητικά) θα κινηθούν σε κάθε δυναμική
γραμμή, δηλ. διαχωρίζει τα θετικά από τα αρνητικά φορτία. Τα παραπάνω
θα γίνουν καλύτερα κατανοητά μελετώντας την ακόλουθη περίπτωση, η
οποία είναι σημαντική σε θέματα σχετικά με μαγνητόσφαιρες των pulsars:
Pulsars είναι αστέρες νετρονίων γρήγορα περιστρεφόμενοι και ισχυρά μαγνητισμένοι1 . Κοντά στο αστέρι το ηλεκτρικό πεδίο έχει μη μηδενική συνιστώσα παράλληλα στο μαγνητικό (βλ. υποσημείωση 1). ΄Ετσι καθώς ένα φορτίο κινείται πάνω σε μία από τις ανοιχτές δυναμικές γραμμές του B επιταχύνεται και
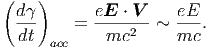 | (8.12) |
Λεπτομέρειες για το πώς μεταβάλλεται το ηλεκτρικό και μαγνητικό πεδίο με την απόσταση και το πού ισχύει B ⋅ E≠0 παραμένουν αντικείμενο έρευνας. (Η εικόνα που περιγράφεται στην υποσημείωση 1 τροποποιείται αφενός λόγω του ότι η μαγνητόσφαιρα δεν παραμένει κενή και αφετέρου γιατί το μαγνητικό πεδίο δεν παραμένει διπολικό αφού πρέπει οι δυναμικές του γραμμές να είναι ανοικτές πέρα από τον κύλινδρο φωτός.) Τυπικές τιμές για τα πεδία κοντά στην επιφάνεια του αστέρα είναι B ~ 1012G και E ~ (RΩ∕c)B ~ 1010sV cm-1, θεωρώντας ακτίνα του αστέρα νετρονίων R = 106cm και περίοδο περιστροφής 0.03s.
΄Εστω ότι ένα ηλεκτρόνιο έχει αποσπαστεί από την επιφάνεια του αστέρα νετρονίων και αρχίζει να επιταχύνεται καθώς κινείται πάνω σε μια δυναμική γραμμή του μαγνητικού πεδίου. Αφού η δυναμική γραμμή είναι καμπύλη η διεύθυνση της ταχύτητας του φορτίου αλλάζει, δηλ. υπάρχει επιτάχυνση, οπότε θα εκπεμφθεί ακτινοβολία λόγω καμπυλότητας της τροχιάς. Η ισχύς της ακτινοβολούμενης ενέργειας, η οποία ισούται με τον ρυθμό μείωσης της ενέργειας του φορτίου, δίνεται από τη γενική σχέση Larmor (άσκηση ??)
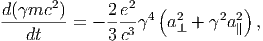 | (8.13) |
όπου a⊥, a∥ είναι οι συνιστώσες της επιτάχυνσης κάθετα και παράλληλα στην ταχύτητα, αντίστοιχα. Η επιτάχυνση λόγω καμπυλότητας των δυναμικών γραμμών είναι κάθετη στην ταχύτητα (κεντρομόλος) με μέτρο a⊥ = V 2∕R≈ c2∕R όπου R είναι η ακτίνα καμπυλότητας της τροχιάς, οπότε
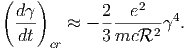 | (8.14) |
(ϒποπερίπτωση αποτελεί η ακτινοβολία σύγχροτρον. Για R = rg = γmc2∕eB παίρνουμε το αποτέλεσμα mc2(dγ∕dt) syn = -(2∕3)(e4∕m2c3)B2γ2 που ήδη έχει βρεθεί στο κεφάλαιο 6.)
Η τελική επιτάχυνση του σωματίου δίνεται από (σε υψηλές ενέργειες οι απώλειες λόγω ακτινοβολίας καμπυλότητας υπερισχύουν έναντι των υπολοίπων)
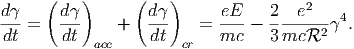 | (8.15) |
Η οριακή τιμή του παράγοντα Lorentz αντιστοιχεί σε dγ∕dt = 0, δηλ.
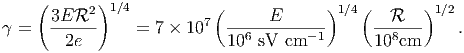 | (8.16) |
Το σωμάτιο λοιπόν θα δώσει ένα φωτόνιο (γ). Το φωτόνιο αυτό με τη σειρά του αλληλεπιδρά με το μαγνητικό πεδίο και μπορεί να δώσει ένα ζεύγος ηλεκτρονίου-ποζιτρονίου (γB → e-e+B). Τα δύο νέα σωμάτια επιταχύνονται και δίνουν νέα φωτόνια κ.ο.κ. Παρουσιάζεται λοιπόν φαινόμενο χιονοστιβάδας το οποίο έχει ως αποτέλεσμα να γεμίσει η μαγνητόσφαιρα με ηλεκτρόνια-ποζιτρόνια.
΄Εστω ότι ένα φορτισμένο σωμάτιο μάζας m κινείται σε χώρο όπου υπάρχουν
διάσπαρτα κατανεμημένοι μαγνητικοί καθρέπτες, οι οποίοι ανακλούν ελαστικά
το σωμάτιο. Οι καθρέπτες κινούνται με ταχύτητα V s « c. Θεωρήστε ότι
το σωμάτιο κινείται αρχικά με μη σχετικιστική ταχύτητα V . Θεωρήστε ότι οι
ταχύτητες V και V s έχουν ίδια διεύθυνση, αλλά όχι απαραίτητα ίδια φορά.
(α) ϒπολογίστε τη διαφορά στην ενέργεια του σωματίου μετά από μία κρούση.
(β) Αφού βρείτε τις πιθανότητες που αντιστοιχούν σε V ↗ ↗ V s και
V ↗ ↙ V s, υπολογίστε το μέσο κέρδος στην ενέργεια του σωματίου μετά
από κάθε κρούση.
(γ) Επαναλάβατε τα προηγούμενα στην περίπτωση όπου η ταχύτητα V είναι
σχετικιστική.
(δ) ΄Εστω L η μέση απόσταση μεταξύ των καθρεπτών. Επίσης θεωρήστε
ότι υπάρχει πλήθος σωματίων στην περιοχή των καθρεπτών, το οποίο –
λόγω της διαφυγής κάποιων από τα σωμάτια – μειώνεται εκθετικά, με χρόνο
υποδιπλασιασμού td. Δείξτε ότι τα σωμάτια που φεύγουν από αυτήν την περιοχή
έχουν ενέργειες με φάσμα έναν νόμο δύναμης του οποίου να βρείτε τον εκθέτη.
Δείξτε ότι στην περίπτωση όπου ένα σωμάτιο κινείται με ταχύτητα V και
ανακλάται ελαστικά από ένα μεγάλης μάζας σώμα που έχει ταχύτητα V s η
ενέργειά του μετά την κρούση δίνεται από τη σχέση (8.1).
Στη συνέχεια δείξτε ότι η πιθανότητα σε μια κρούση η γωνία θ ∈ ![[0, π]](HEA_files/HEA283x.png) μεταξύ V s και V να είναι από θ ως θ + dθ είναι (1∕2)
μεταξύ V s και V να είναι από θ ως θ + dθ είναι (1∕2)![[1 - (Vs ∕c)cosθ]](HEA_files/HEA284x.png) sin θdθ.
(Θεωρήστε ότι το σωμάτιο έχει ταχύτητα V ≈ c.)
sin θdθ.
(Θεωρήστε ότι το σωμάτιο έχει ταχύτητα V ≈ c.)
Δείχνοντας πρώτα ότι η μέση τιμή < cos θ > είναι -V s∕3c, βρείτε το μέσο
κέρδος σε ενέργεια < Δγ∕γ > μετά από μια κρούση, στο όριο που V s « c.
Πλήθος σωματίων N0 με αρχική ενέργεια E0 επιταχύνεται σε ασυνέχεια
ροής. Θεωρούμε ότι μετά από κάθε κύκλο η ενέργεια ενός σωματίου γίνεται ε
επί την ενέργεια που είχε στην αρχή του κύκλου, με ε =σταθερά (μεγαλύτερη
της μονάδας).
(α) Ποια η ενέργεια Ek σωματίων μετά από k κύκλους;
(β) Αν η πιθανότητα παραμονής σωματίου μετά από κάθε κύκλο είναι p, με
p =σταθ., πόσα σωμάτια συνεχίζουν να επιταχύνονται μετά από k κύκλους
(και άρα αποκτούν ενέργεια μεγαλύτερη από Ek); Συγκεκριμένα δείξτε ότι
N(> E) = N0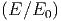 -s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του
νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Δείξτε ότι στο όριο
p ≈ 1-, ε ≈ 1+ ο εκθέτης του νόμου δύναμης είναι 1 + (1 - p)∕(ε - 1).
-s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του
νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Δείξτε ότι στο όριο
p ≈ 1-, ε ≈ 1+ ο εκθέτης του νόμου δύναμης είναι 1 + (1 - p)∕(ε - 1).
(γ) ΄Εστω ότι η πιθανότητα παραμονής σωματίου μετά από κάθε κύκλο p
δεν είναι σταθερή, αλλά μειώνεται όσο η ενέργεια αυξάνει. Θεωρούμε ότι η
μείωση αυτή περιγράφεται από νόμο δύναμης, δηλ. ότι η πιθανότητα ένα σωμάτιο
που έχει ήδη κάνει k - 1 κύκλους, να μείνει στην περιοχή της επιτάχυνσης
εκτελώντας τον k κύκλο, δίδεται από τη σχέση pk = g∕Ekq, όπου g και
q θετικές σταθερές. Δείξτε ότι N(> E) = N0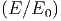 -
-![[s-1+rln(E∕E0)]](HEA_files/HEA287x.png) με
s = 1 - q∕2 - ln(g∕E0q)∕ ln ε, r = q∕(2 ln ε). Ποιο είναι το ενεργειακό φάσμα
dN∕dE σε αυτήν την περίπτωση; Σκεπτόμενοι ότι οι λογάριθμοι αλλάζουν πολύ
αργά σε σχέση με τις δυνάμεις, απλοποιήστε τη σχέση που δίνει το φάσμα και
συμπεράνετε ότι το φάσμα είναι νόμος δύναμης με μεταβλητό εκθέτη.
με
s = 1 - q∕2 - ln(g∕E0q)∕ ln ε, r = q∕(2 ln ε). Ποιο είναι το ενεργειακό φάσμα
dN∕dE σε αυτήν την περίπτωση; Σκεπτόμενοι ότι οι λογάριθμοι αλλάζουν πολύ
αργά σε σχέση με τις δυνάμεις, απλοποιήστε τη σχέση που δίνει το φάσμα και
συμπεράνετε ότι το φάσμα είναι νόμος δύναμης με μεταβλητό εκθέτη.
(δ) ΄Εστω ότι η πιθανότητα παραμονής σωματίου μένει σταθερή για μικρές τιμές
της ενέργειας, E « Ec, ενώ μειώνεται για μεγαλύτερες τιμές. Αυτό μπορεί να
περιγραφεί με τη σχέση pk = g∕![q
[1 + (Ek∕Ec ) ]](HEA_files/HEA288x.png) . Συνδυάζοντας τις απαντήσεις
στα (β), (γ) και χωρίς να κάνετε πράξεις, ποιο περιμένετε να είναι το φάσμα;
. Συνδυάζοντας τις απαντήσεις
στα (β), (γ) και χωρίς να κάνετε πράξεις, ποιο περιμένετε να είναι το φάσμα;
(α) Περιγράψτε ποιοτικά την επιτάχυνση φορτισμένων σωματίων στην περίπτωση
ολίσθησης πάνω σε επιφάνεια ασυνέχειας η οποία κινείται κάθετα σε μαγνητικό
πεδίο.
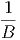 =
=
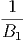 -
- 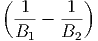
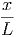 . Δείξτε ότι
η ενέργεια ενός σωματίου αυξάνει
εκθετικά
με χρόνο υπερδιπλασιασμού ta ln 2,
όπου ta =
. Δείξτε ότι
η ενέργεια ενός σωματίου αυξάνει
εκθετικά
με χρόνο υπερδιπλασιασμού ta ln 2,
όπου ta = 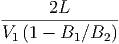 .
.
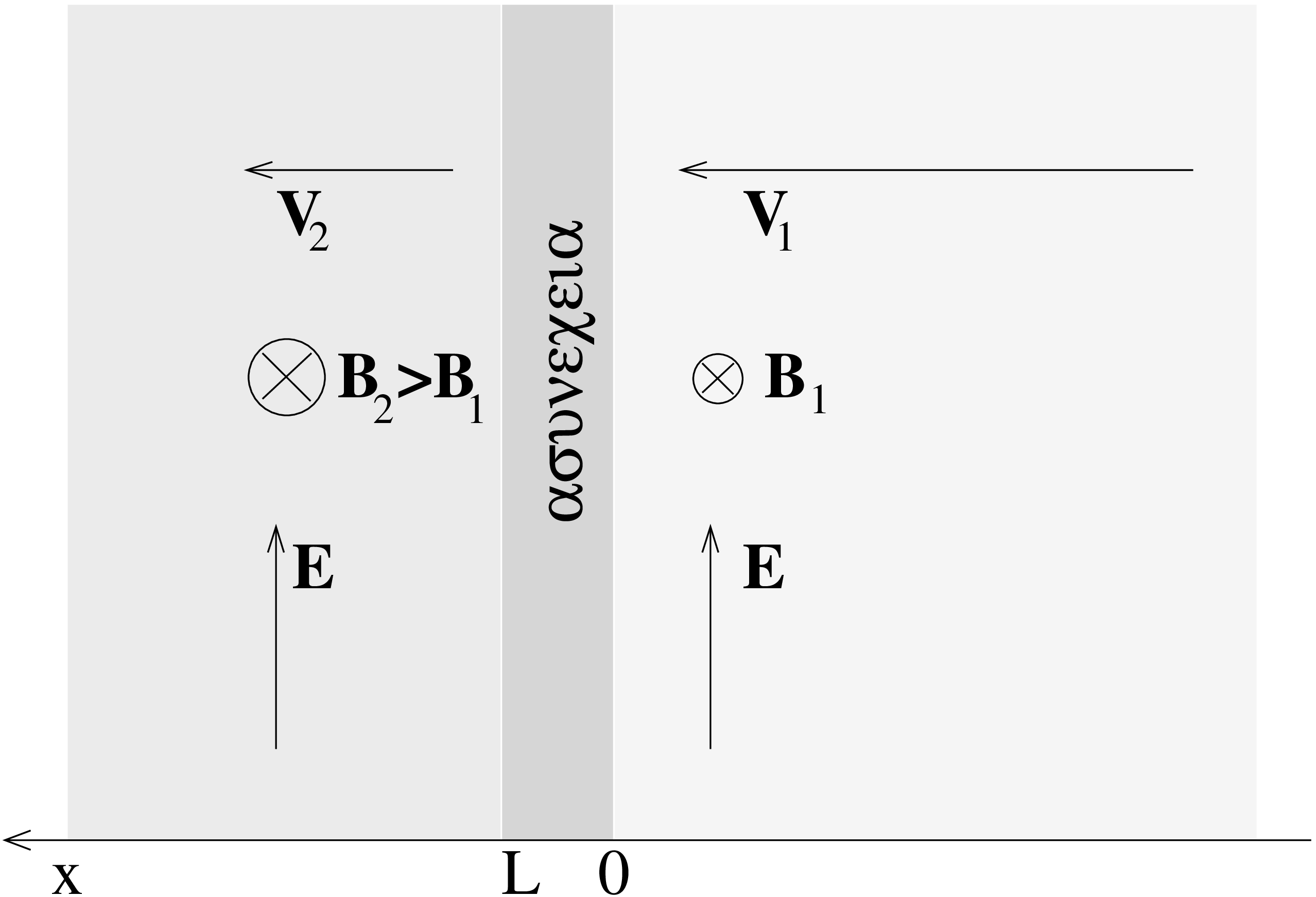
΄Εστω ένα μαγνητισμένο νέφος που κινείται με ταχύτητα V . Αν το υλικό
του νέφους παρουσιάζει άπειρη αγωγιμότητα ποια η σχέση μεταξύ ηλεκτρικού
(E) και μαγνητικού (B) πεδίου;
Φορτίο q κινείται με μη-σχετικιστική ταχύτητα w στην περιοχή του νέφους.
Δείξτε ότι η εξίσωση κίνησης γράφεται 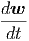 =
= 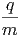
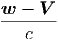 ×B.
×B.
Δείξτε ότι ο ρυθμός αύξησης της ενέργειας του φορτίου είναι qV ⋅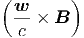 ,
δηλ. σχετίζεται με το έργο της δύναμης που ασκεί το φορτίο στο νέφος.
,
δηλ. σχετίζεται με το έργο της δύναμης που ασκεί το φορτίο στο νέφος.
Δείξτε ότι το προηγούμενο συμπέρασμα παραμένει ίδιο και στην περίπτωση
σχετικιστικής κίνησης του φορτίου.
(α) Ποια η διαφορά μεταξύ των μηχανισμών επιτάχυνσης Fermi πρώτης και
δεύτερης τάξης;
(β) Πώς υλοποιείται ο μηχανισμός δεύτερης τάξης σύμφωνα με την αρχική ιδέα
του Fermi και ποια είναι τα μειονεκτήματά του στο να εξηγήσει παρατηρήσεις;
(γ) Περιγράψτε ποιοτικά πώς υλοποιείται ο μηχανισμός επιτάχυνσης Fermi
πρώτης τάξης σε ασυνέχειες ροής πλάσματος.
(δ) Πλήθος σωματίων N0 με αρχική ενέργεια E0 επιταχύνεται σε ασυνέχεια
ροής. Αν μετά από κάθε κύκλο η ενέργεια ενός σωματίου αυξάνει κατά
ΔE = nE με n = σταθ., ποια η ενέργειά του μετά από k κύκλους; Αν η
πιθανότητα διαφυγής σωματίου μετά από κάθε κύκλο είναι P, πόσα σωμάτια
συνεχίζουν να επιταχύνονται μετά από k κύκλους; Ποιος είναι ο εκθέτης του
νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Δείξτε ότι στο όριο
P « 1, n « 1 ο εκθέτης του νόμου δύναμης είναι 1 + P∕n.
(α) Περιγράψτε την επιτάχυνση σωματίων στις μαγνητόσφαιρες των pulsars
όπου το μαγνητικό πεδίο έχει δυναμικές γραμμές με ακτίνα καμπυλότητας R
και υπάρχει ηλεκτρικό πεδίο E παράλληλα στις δυναμικές γραμμές του B. Ποια
η μέγιστη τιμή του παράγοντα Lorentz που αποκτούν τα σωμάτια;
(β) ΄Εστω ότι οι δυναμικές γραμμές του B είναι aktinikc (οπότε R = ∞).
Αφού σκεφτείτε σε ποιο μηχανισμό ακτινοβολίας οφείλονται τώρα οι απώλειες,
γράψτε τη διαφορική εξίσωση για τον παράγοντα Lorentz και βρείτε τη μέγιστη
τιμή του.
(Δίδεται η σχέση Larmor P = 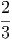
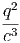 γ4
γ4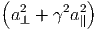 για την ακτινοβολία από
ένα φορτίο q.)
για την ακτινοβολία από
ένα φορτίο q.)
Στη γειτονιά μιας μελανής οπής με μάζα M = M8 × 108M
⊙ και σε
αποστάσεις r = r1rS (όπου rS = 2GM∕c2 η ακτίνα Schwarzschild), το υλικό
του δίσκου προσαύξησης περιστρέφεται κεπλεριανά.
(α) Αν στην περιοχή αυτή υπάρχει μαγνητικό πεδίο B4 × 104G, ποιο το
ηλεκτρικό πεδίο;
(β) Ποια η μέγιστη ενέργεια γmaxmc2 που αποκτούν σωμάτια φορτίου q = q
1e
και μάζας m = m1mp σ΄ αυτήν την περιοχή αν η ακτίνα καμπυλότητας του
πεδίου B είναι R = R1r; Εξαρτάται το αποτέλεσμα από τη μάζα του σωματίου;
(γ) Δείξτε ότι ο χρόνος που απαιτείται για την επιτάχυνση σε γmax είναι
~ γmaxmc∕qE και υπολογίστε τον στην περίπτωση ενός πρωτονίου όταν
r1 = R1 = B4 = M8 = 1.
(δ) Για δεδομένα r1 = R1 = B4 = M8 = 1, πώς θα μπορούσαμε να
πάρουμε σωμάτια με ενέργεια 1020eV; Πόσος χρόνος θα χρειαζόταν γι΄ αυτήν
την επιτάχυνση και πόση απόσταση διανύει το φορτίο σε αυτόν τον χρόνο;
Συγκρίνετε αυτήν την απόσταση με την ακτίνα Schwarzschild και συμπεράνετε
αν είναι καλή προσέγγιση να θεωρούμε το πεδίο E σταθερό.
Δίδεται η σχέση Larmor για την ακτινοβολία από ένα φορτίο q:
P = 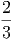
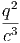 γ4
γ4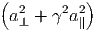 . Επίσης e = 4.8 × 10-10 esu, c = 3 × 1010cm s-1,
G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g, m
p = 1.67 × 10-24g,
1eV=1.6 × 10-12ergs.
. Επίσης e = 4.8 × 10-10 esu, c = 3 × 1010cm s-1,
G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g, m
p = 1.67 × 10-24g,
1eV=1.6 × 10-12ergs.
Πλήθος σωματίων N0 με αρχική ενέργεια E0 επιταχύνεται σε ωστικό κύμα.
Θεωρούμε ότι μετά από κάθε κύκλο η ενέργεια ενός σωματίου γίνεται ε επί
την ενέργεια που είχε στην αρχή του κύκλου, με ε =σταθερά (μεγαλύτερη της
μονάδας).
(α) Ποια η ενέργεια Ek σωματίων μετά από k κύκλους;
(β) Αν η πιθανότητα παραμονής σωματίου μετά από κάθε κύκλο είναι p, με
p = σταθ., πόσα σωμάτια συνεχίζουν να επιταχύνονται μετά από k κύκλους
(και άρα αποκτούν ενέργεια μεγαλύτερη από Ek); Συγκεκριμένα δείξτε ότι
N(> E) = N0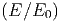 -s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του
νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Δείξτε ότι στο όριο
p ≈ 1-, ε ≈ 1+ ο εκθέτης είναι 1 + (1 - p)∕(ε - 1).
-s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του
νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Δείξτε ότι στο όριο
p ≈ 1-, ε ≈ 1+ ο εκθέτης είναι 1 + (1 - p)∕(ε - 1).
(γ) Σε ένα ωστικό κύμα επιταχύνονται ηλεκτρόνια. Θεωρήστε γνωστό ότι
ο χρόνος που χρειάζεται ένα ηλεκτρόνιο για να αποκτήσει ενέργεια E είναι
tacc = 4cηE∕3V sh2eB, όπου V
sh η ταχύτητα του ωστικού κύματος, B το
μαγνητικό πεδίο στην περιοχή επιτάχυνσης και η μια σταθερά. Λαμβάνοντας
υπόψη την ακτινοβολία σύγχροτρον (αφού τα ηλεκτρόνια βρίσκονται μέσα σε
μαγνητικό πεδίο ακτινοβολούν), υπολογίστε τη μέγιστη ενέργεια Emax που
μπορούν να αποκτήσουν. ϒπόδειξη: Βρείτε πρώτα το πόσος χρόνος απαιτείται
για να ακτινοβολήσει ένα ηλεκτρόνιο όλη του την ενέργεια, χρησιμοποιώντας
τη σχέση Ėsyn = (4∕3)σT cUB(E∕mc2)2.
Γνωρίζοντας ότι ηλεκτρόνια ενέργειας E εκπέμπουν φωτόνια ενέργειας hνsyn =
mc2(E∕mc2)2(B∕B
cr), όπου Bcr = 2πm2c3∕eh, ποια η μέγιστη συχνότητα του
φάσματος που εκπέμπεται;
(α) Η επιτάχυνση Fermi δεύτερης τάξης οδηγεί σε ενεργειακό φάσμα
∝ E-1-ta∕tddE, όπου t
a = 3cL∕4V s2. Ποιο το μηχανικό της ανάλογο και τι
σημαίνουν τα διάφορα σύμβολα των προηγούμενων σχέσεων; Μπορούν να
επιταχυνθούν ουδέτερα σωμάτια με αυτόν τον μηχανισμό; Ποια τα μειονεκτήματα του
μηχανισμού αυτού; Ποια η βελτιωμένη έκδοση του μηχανισμού Fermi; (Αναφέρατε
μόνο το μηχανικό της ανάλογο.)
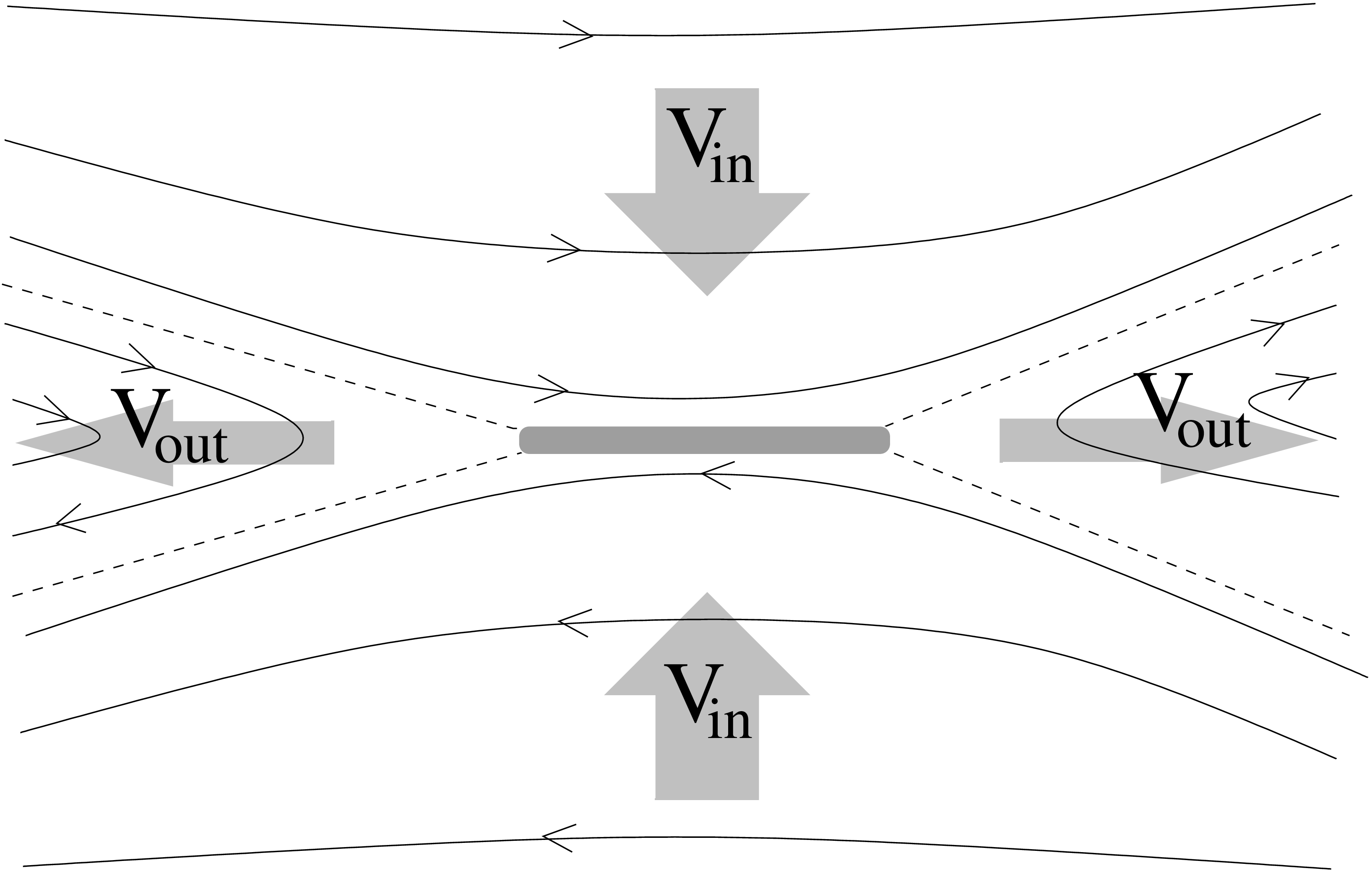
(α) Πλήθος σωματίων N0 με αρχική ενέργεια E0 επιταχύνεται σε ωστικό
κύμα. Μετά από κάθε κύκλο η ενέργεια ενός σωματίου γίνεται ε επί την
ενέργεια που είχε στην αρχή του κύκλου, με ε = 1 + (4∕3)(1 - 1∕r)(V s∕c),
όπου V s η ταχύτητα του ωστικού κύματος και r ο λόγος συμπίεσης. Για
ισχυρά ωστικά κύματα (στα οποία η ταχύτητα V s είναι πολύ μεγαλύτερη από
την ταχύτητα διάδοσης κυμάτων μέσα στο ρευστό), ο λόγος συμπίεσης είναι
r = (Γ + 1)∕(Γ - 1), όπου Γ ο πολυτροπικός δείκτης (Γ = 1 + 2∕f, όπου f το
πλήθος των βαθμών ελευθερίας). Η πιθανότητα παραμονής σωματίου μετά από
κάθε κύκλο είναι p = 1 - (4∕r)(V s∕c). Δείξτε ότι το πλήθος των σωματίων
που αποκτούν ενέργεια μεγαλύτερη από E είναι N(> E) = N0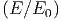 -s+1 με
s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του νόμου δύναμης του ενεργειακού
φάσματος που παράγεται; Ποια η προσεγγιστική τιμή του σαν συνάρτηση του
Γ, αν V s « c;
-s+1 με
s = 1 - ln p∕ ln ε. Ποιος είναι ο εκθέτης του νόμου δύναμης του ενεργειακού
φάσματος που παράγεται; Ποια η προσεγγιστική τιμή του σαν συνάρτηση του
Γ, αν V s « c;
(β) Το ωστικό κύμα ενός υπερκαινοφανούς κινείται με ταχύτητα vs =
104km s-1 μέσα στον μεσοαστρικό χώρο, για τον οποίο υποθέτουμε πυκνότητα
ένα άτομο υδρογόνου ανά cm3, θερμοκρασία T = 104Κ και μαγνητικό πεδίο
B = 3 μG. Μπορεί να θεωρηθεί το ωστικό κύμα ισχυρό; (Λάβετε υπόψη τα
κύματα ήχου με ταχύτητα cs = 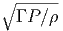 και τα κύματα Alfvιn με ταχύτητα
vA = B∕
και τα κύματα Alfvιn με ταχύτητα
vA = B∕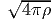 .) Ποιος ο εκθέτης του ενεργειακού φάσματος των κοσμικών
ακτίνων που προέρχονται από τον υπερκαινοφανή; (Θεωρήστε μονατομικό
αέριο.)
.) Ποιος ο εκθέτης του ενεργειακού φάσματος των κοσμικών
ακτίνων που προέρχονται από τον υπερκαινοφανή; (Θεωρήστε μονατομικό
αέριο.)
Δίνεται η μάζα του πρωτονίου 1∕(6.023×1023) g και η σταθερά του Boltzmann
kB = 1.38 × 10-16 (cgs).
(α) Περιγράψτε την επιτάχυνση σωματίων σε υψηλές ενέργειες από
μεταβολές δυναμικού στη μαγνητόσφαιρα αστέρων νετρονίων. Ποιος ο ρυθμός
αύξησης του παράγοντα Lorentz; ϒπολογίστε τον αριθμητικά για ηλεκτρόνια
(me = 9.1 × 10-28g, e = 4.8 × 10-10cgs), που επιταχύνονται σε αστέρα με
R = 106cm, B = 1012G και Ω = 200 rad s-1.
(β) Μέχρι πότε συνεχίζεται η αύξηση του παράγοντα Lorentz; Αναφέρατε τρεις
λόγους που μπορούν να σταματήσουν την επιτάχυνση και σχολιάστε ποιος είναι
ο κυρίαρχος και γιατί. Ποια η μέγιστη τιμή του παράγοντα Lorentz;
Δίνεται P = 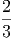
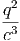 γ4
γ4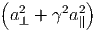 και c = 3 × 1010 cm s-1.
και c = 3 × 1010 cm s-1.
(α) Σε ποια από τις γνωστές μορφές δύναμης στη φύση οφείλεται η
επιτάχυνση Fermi;
(β) Ποιο το μηχανικό ανάλογο της δεύτερης τάξης επιτάχυνσης Fermi;
(γ) Μπορεί η δεύτερης τάξης επιτάχυνση Fermi να εξηγήσει το φάσμα των
κοσμικών ακτίνων;
(α) Πού οφείλονται οι ελαστικές ανακλάσεις που είναι απαραίτητες για την
υλοποίηση του μηχανισμού επιτάχυνσης τύπου Fermi;
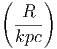
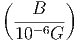 ×
1018eV . ΄Ετσι προκύπτει
το διάγραμμα του Hillas (Hillas, A.
M. 1984, ARA&A, 22, 425), στο
οποίο φαίνονται οι πιθανοί τόποι
επιτάχυνσης σε δεδομένη ενέργεια
E.
×
1018eV . ΄Ετσι προκύπτει
το διάγραμμα του Hillas (Hillas, A.
M. 1984, ARA&A, 22, 425), στο
οποίο φαίνονται οι πιθανοί τόποι
επιτάχυνσης σε δεδομένη ενέργεια
E. 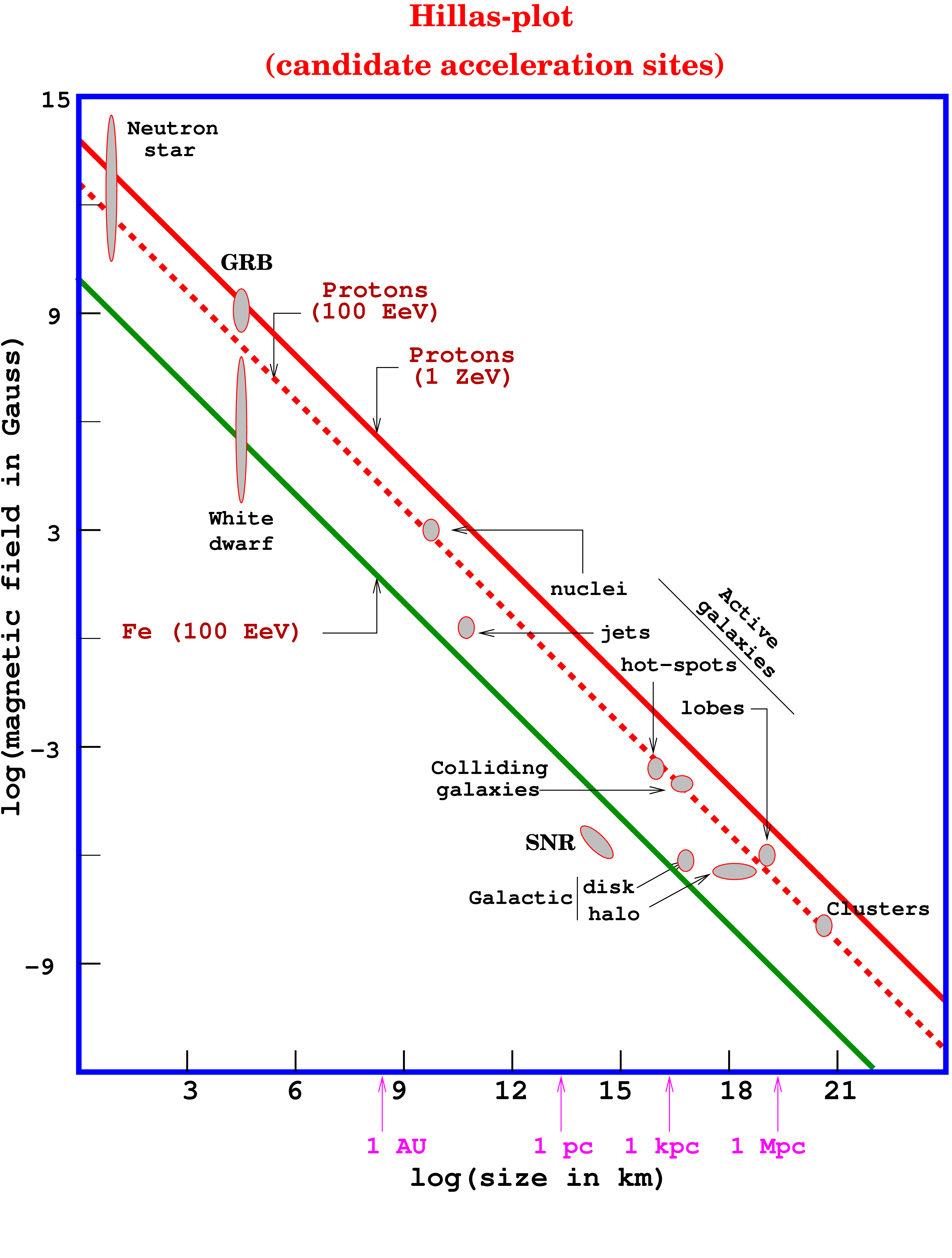
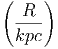
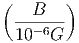
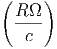 × 1018eV , όπου R η
ακτίνα και Ω η γωνιακή ταχύτητα του αντικειμένου. (Θεωρήστε ότι και η
μαγνητόσφαιρα έχει ίδια διάσταση R.)
× 1018eV , όπου R η
ακτίνα και Ω η γωνιακή ταχύτητα του αντικειμένου. (Θεωρήστε ότι και η
μαγνητόσφαιρα έχει ίδια διάσταση R.)
(α) Περιγράψτε περιληπτικά την επιτάχυνση Fermi σε μια ισχυρή ασυνέχεια ροής.
΄Εστω αρχικά έχουμε πρωτόνια με θερμική κατανομή θερμοκρασίας T « mpc2∕k
B.
Ποια η ενέργεια κάθε σωματίου μετά από n περάσματα από την ασυνέχεια (δηλ. n∕2
κύκλους);
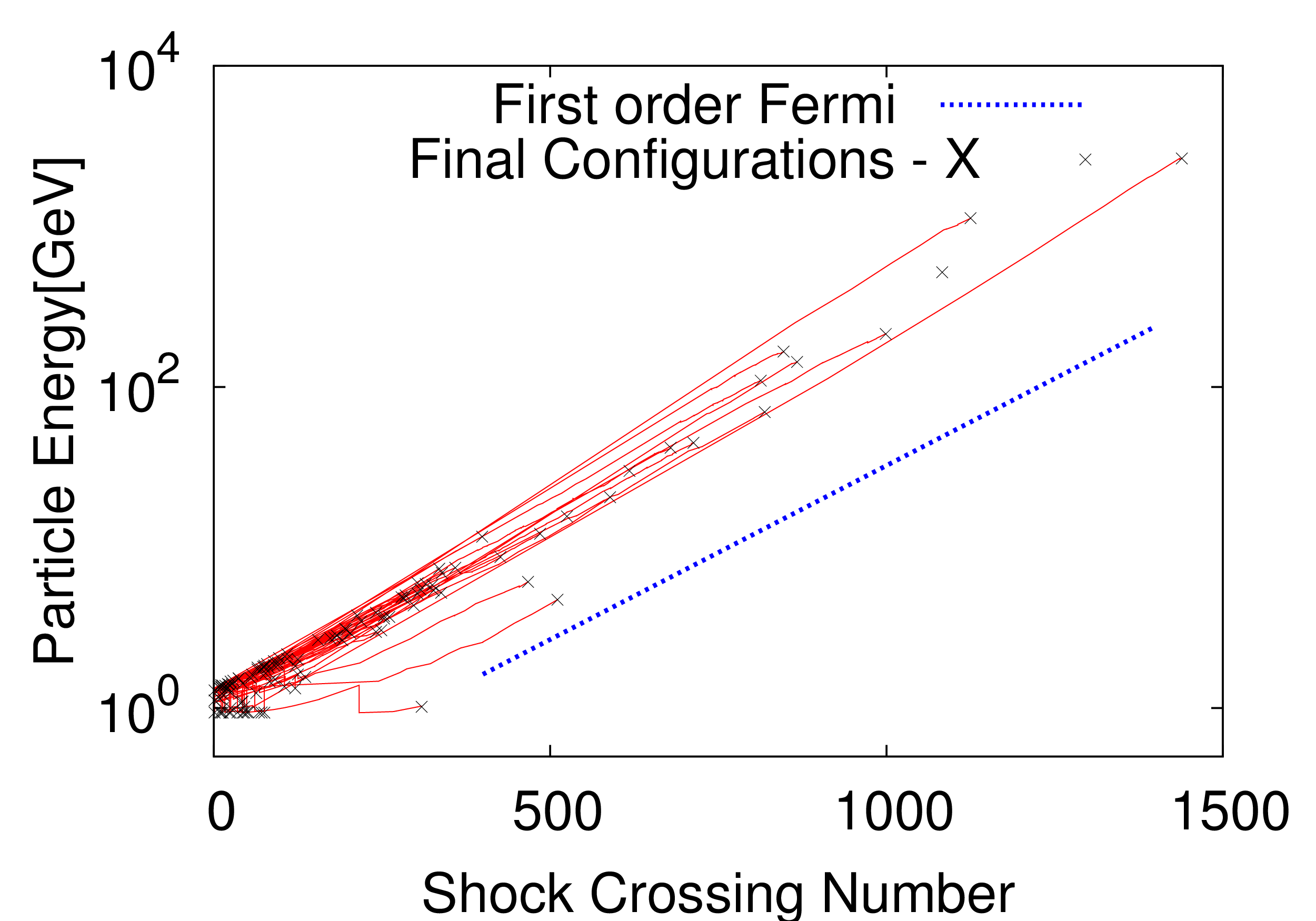
Συμφωνούν τα αποτελέσματα αυτά με τη θεωρία της επιτάχυνσης Fermi; Τι μπορούμε να βρούμε από την κλίση της εστιγμένης γραμμής; (Δώστε το σχετικό αποτέλεσμα.)
Ηλεκτρόνια επιταχύνονται στις μαγνητόσφαιρες των pulsars λόγω της
ύπαρξης ηλεκτρικού πεδίου με μη-μηδενική συνιστώσα E∥ πάνω στην ταχύτητα
των φορτίων cβ (με β ≈ 1). Θεωρούμε ότι η επιτάχυνση λαμβάνει χώρα τοπικά,
δηλ. οι τιμές του ηλεκτρικού πεδίου (E∥), του μαγνητικού πεδίου B και της
καμπυλότητας R των δυναμικών γραμμών του πεδίου B παραμένουν πρακτικά
σταθερές όσο το φορτίο επιταχύνεται.
(α) ϒπολογίστε τον χρόνο ta = γ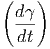 a-1 στον οποίο ο παράγοντας Lorentz
κάποιου ηλεκτρονίου γίνεται γ.
a-1 στον οποίο ο παράγοντας Lorentz
κάποιου ηλεκτρονίου γίνεται γ.
(β) Λόγω του μαγνητικού πεδίου το ηλεκτρόνιο επιταχύνεται – και άρα
ακτινοβολεί – με δυο τρόπους:
(β1) Ακτινοβολία καμπυλότητας δημιουργείται αν το ηλεκτρόνιο κινείται
κυρίως κατά μήκος του B, λόγω της καμπυλότητας της τροχιάς R. Αν
ο παράγοντας Lorentz του φορτίου είναι γ, υπολογίστε τον χρόνο tc =
γ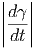 c-1 στον οποίο ακτινοβολείται όλη η ενέργεια του φορτίου μέσω
της ακτινοβολίας καμπυλότητας. Δίδεται ο ρυθμός ελάττωσης της ενέργειας
φορτίου e που ακτινοβολεί λόγω επιτάχυνσης c
c-1 στον οποίο ακτινοβολείται όλη η ενέργεια του φορτίου μέσω
της ακτινοβολίας καμπυλότητας. Δίδεται ο ρυθμός ελάττωσης της ενέργειας
φορτίου e που ακτινοβολεί λόγω επιτάχυνσης c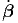 : (2e2∕3c)γ6
: (2e2∕3c)γ6![[ ˙ 2 ˙ 2]
(β) - (β × β )](HEA_files/HEA319x.png) (σχέση Larmor).
(σχέση Larmor).
(β2) Ακτινοβολία σύγχροτρον δημιουργείται λόγω της ταχύτητας cβ⊥ κάθετα
στο μαγνητικό πεδίο. ϒπολογίστε τον χρόνο ts στον οποίο το φορτίο χάνει
όλη την ενέργειά του (γmc2) λόγω ακτινοβολίας σύγχροτρον. Δίδεται για την
κίνηση ηλεκτρονίου σε μαγνητικό πεδίο 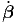 =
= 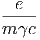 β×B, με μέτρο
β×B, με μέτρο 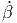 =
= 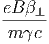 .
.
(γ) Στις μαγνητόσφαιρες, η επιτάχυνση λόγω ηλεκτρικού πεδίου δημιουργεί
κίνηση κυρίως κατά μήκος του πεδίου B, οπότε η κυρίαρχη επιτάχυνση
οφείλεται στην καμπυλότητα R. Αν B = 106 G, E
∥ = B, R = 108 cm (δίνονται
επίσης e = -4.8 × 10-10, m = 9.1 × 10-28, c = 3 × 1010, όλα σε μονάδες cgs),
βρείτε τους χρόνους ta και tc σαν συναρτήσεις του παράγοντα Lorentz γ και
σχεδιάστε τους σε διάγραμμα log γ – log t. Με τη βοήθεια του διαγράμματος
αυτού βρείτε τον μέγιστο παράγοντα Lorentz και τον χρόνο επιτάχυνσης. Είναι
δικαιολογημένη η υπόθεση της τοπικής επιτάχυνσης;
(δ) Πόση πρέπει να είναι το πολύ η συνιστώσα της ταχύτητας κάθετα στο
μαγνητικό πεδίο cβ⊥ ώστε οι απώλειες σύγχροτρον να είναι πράγματι αμελητέες;
(Το ερώτημα αφορά μαγνητόσφαιρα με τα χαρακτηριστικά του προηγούμενου
ερωτήματος.)
΄Εστω μία κυλινδρική εκροή ακτίνας ϖj στην οποία η ταχύτητα έχει σταθερή
διεύθυνση παράλληλη στον άξονα συμμετρίας, αλλά όχι σταθερό μέτρο,
v = v(ϖ)ẑ. Αν υπάρχουν ανομοιογένειες στο μαγνητικό πεδίο της εκροής,
σωματίδια που κινούνται μεταξύ στρωμάτων με διαφορετικές μακροσκοπικές
ταχύτητες θα επιταχύνονται κατά Fermi.
(α) Τι τάξης θα είναι η επιτάχυνση Fermi, πρώτης ή δεύτερης;
(β) Οι Rieger & Duffy 2004, ApJ 617, 155 υπολόγισαν ότι αν ο παράγοντας
Lorentz ελαττώνεται γραμμικά από γb στον άξονα (ϖ = 0) σε ≈ 1 στην
επιφάνεια του κυλίνδρου (ϖ = ϖj), ο χρόνος επιτάχυνσης είναι tacc = 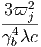 ,
όπου λ ≈ rg η μέση ελεύθερη διαδρομή, ίση περίπου με την ακτίνα Larmor
rg ≈ γmc2∕|q|B
co. Θεωρώντας |q| = e, δείξτε ότι οι απώλειες σύγχροτρον δεν
είναι σημαντικές για ϖj < 0.1γb2
,
όπου λ ≈ rg η μέση ελεύθερη διαδρομή, ίση περίπου με την ακτίνα Larmor
rg ≈ γmc2∕|q|B
co. Θεωρώντας |q| = e, δείξτε ότι οι απώλειες σύγχροτρον δεν
είναι σημαντικές για ϖj < 0.1γb2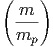 2
2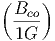 -3∕2 pc.
-3∕2 pc.
Δίνεται ο χρόνος για την ψύξη σύγχροτρον tsyn = 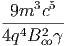 .
.
(γ) Ποια η μέγιστη ενέργεια που αποκτούν πρωτόνια επιταχυνόμενα στη ροή,
αν ϖj = 10 pc, Bco = 10-2 G και γ
b = 10; Αλλάζει αυτό το αποτέλεσμα αν
αντί πρωτονίων επιταχύνονται ηλεκτρόνια ή πυρήνες σιδήρου;
Δίνονται οι σταθερές e = 4.8 × 10-10, m
p = 9.1 × 10-28, c = 3 × 1010, 1 pc =
3 × 1018, 1 eV = 1.6 × 10-12, όλες σε μονάδες cgs.
(α) Τι θερμοκρασία θα έπρεπε να έχει μια αστροφυσική πηγή ώστε να μπορεί
(σε ένα υποθετικό σενάριο) να επιταχύνει θερμικά πυρήνες σιδήρου σε ενέργεια
1020eV;
(β) Θα μπορούσαν οι κοσμικές ακτίνες που φτάνουν στη γη να έχουν
επιταχυνθεί βαρυτικά;
(γ) Μπορούν πρωτόνια ενέργειας 1018eV να έχουν επιταχυνθεί σε υπόλειμμα
υπερκαινοφανούς διαστάσεων 2 pc στο οποίο το μαγνητικό πεδίο είναι B ≈ 10-6
G;
(δ) Δώστε ένα απλό μηχανικό ανάλογο της επιτάχυνσης Fermi prthc τάξης.
Αναλύστε το ανάλογο αυτό, βρίσκοντας το μέσο ενεργειακό κέρδος ανά κύκλο.
Δίδονται 1 pc = 3×1018, e = 4.8×10-10, 1 eV= 1.6×10-12, k
B = 1.38×10-16,
όλα στο Gauss σύστημα μονάδων.
(α) Πλήθος σωματίων N0 με αρχική ενέργεια E0 επιταχύνεται σε ωστικό
κύμα. Μετά από κάθε κύκλο η ενέργεια κάθε σωματίου αυξάνεται γεωμετρικά
με λόγο ε = 1+(4∕3)(1-1∕r)(V∕c), όπου V η ταχύτητα του ωστικού κύματος
και r ο λόγος συμπίεσης, ο οποίος για ισχυρά ωστικά κύματα είναι r = 4. Η
πιθανότητα παραμονής σωματίου μετά από κάθε κύκλο είναι p = 1-(4∕r)(V∕c).
Δείξτε ότι το πλήθος των σωματίων που αποκτούν ενέργεια μεγαλύτερη από
E είναι N(> E) = N0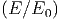 -s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο
εκθέτης του νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Ποια η
προσεγγιστική τιμή του αν V « c;
-s+1 με s = 1 - ln p∕ ln ε. Ποιος είναι ο
εκθέτης του νόμου δύναμης του ενεργειακού φάσματος που παράγεται; Ποια η
προσεγγιστική τιμή του αν V « c;
(β) Το ωστικό κύμα ενός υπερκαινοφανούς κινείται με ταχύτητα 104km s-1
μέσα στον μεσοαστρικό χώρο, για τον οποίο υποθέτουμε πυκνότητα 1 cm-3,
θερμοκρασία 104Κ και μαγνητικό πεδίο 3 μG. Μπορεί να θεωρηθεί το ωστικό
κύμα ισχυρό; (Λάβετε υπόψη τα κύματα ήχου με ταχύτητα cs = 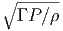 ,
Γ = 5∕3 και τα κύματα Alfvιn με ταχύτητα vA = B∕
,
Γ = 5∕3 και τα κύματα Alfvιn με ταχύτητα vA = B∕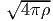 .) Ποιος ο εκθέτης
του ενεργειακού φάσματος των κοσμικών ακτίνων που επιταχύνονται στον
υπερκαινοφανή; Εμείς θα παρατηρήσουμε αυτό το φάσμα από τη Γη;
.) Ποιος ο εκθέτης
του ενεργειακού φάσματος των κοσμικών ακτίνων που επιταχύνονται στον
υπερκαινοφανή; Εμείς θα παρατηρήσουμε αυτό το φάσμα από τη Γη;
Δίνεται η μάζα του πρωτονίου 1∕(6.023×1023) g, και η σταθερά του Boltzmann
kB = 1.38 × 10-16 (cgs).
(α) Σωματίδια επιταχύνονται σε κάποιο αστροφυσικό περιβάλλον, με τρόπο
ώστε η ενέργειά τους να αυξάνεται σαν μια δύναμη του χρόνου, E ∝ tn. Αν
το πλήθος των σωματιδίων που συνεχίζουν να επιταχύνονται μετά από χρόνο
t ελαττώνεται σαν N ∝ t-m δείξτε ότι το ενεργειακό φάσμα που παρατηρούμε
είναι νόμος δύναμης και βρείτε τον εκθέτη.
(β) Αλλάζει το φάσμα αν E ∝ fn και N ∝ f-m, όπου f είναι μια οποιαδήποτε
συνάρτηση του χρόνου; Ποια είναι η f(t) που αντιστοιχεί στην επιτάχυνση
Fermi δεύτερης τάξης;
΄Εστω ένα σωμάτιο ενέργειας E κινείται σχετικιστικά με ταχύτητα V ≈ c
και ανακλάται ελαστικά από ένα μεγάλης μάζας σώμα που έχει ταχύτητα V s.
Θεωρήστε δεδομένο ότι η ενέργεια του σωματίου μετά την κρούση είναι E+ΔE,
όπου ΔE = 2V s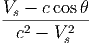 E και θ η γωνία μεταξύ V s και V .
E και θ η γωνία μεταξύ V s και V .
(α) Στην 2ης τάξης επιτάχυνση Fermi η γωνία θ μπορεί να πάρει οποιαδήποτε
τιμή στο διάστημα ![[0,π]](HEA_files/HEA332x.png) . Δείξτε ότι η πιθανότητα να είναι στο διάστημα από
θ ως θ + dθ είναι
. Δείξτε ότι η πιθανότητα να είναι στο διάστημα από
θ ως θ + dθ είναι 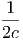
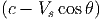 sin θ dθ.
sin θ dθ.
Δείχνοντας πρώτα ότι η μέση τιμή < cos θ > είναι -V s∕3c, βρείτε το μέσο
κέρδος σε ενέργεια < ΔE∕E > μετά από μια κρούση.
(β) Επαναλάβατε για την επιτάχυνση Fermi 1ης τάξης. (Τι τιμές μπορεί να πάρει
η γωνία θ σε αυτή την περίπτωση;)
(γ) Αναφέρετε συνοπτικά πώς υλοποιούνται οι ελαστικές ανακλάσεις σε
αστροφυσικά συστήματα.
(α) Θέλουμε να εξετάσουμε ποιας ενέργειας κοσμικές ακτίνες επηρεάζονται
από το μαγνητικό πεδίο της ηλιόσφαιρας B ~ 10 μG. Βρείτε την ενέργεια που
αντιστοιχεί σε γυροακτίνα ίση με τη διάσταση της ηλιόσφαιρας L ~ 100 AU.
(β) ΄Ομοια για το μεσοαστρικό χώρο με χαρακτηριστική διάσταση L ~ 100 pc
και μαγνητικό πεδίο B ~ 5 μG.
(γ) Εκτιμήστε τη μέγιστη ενέργεια φορτισμένων σωματίων που επιταχύνονται
στις μαγνητόσφαιρες των pulsars (χωρίς να λάβετε υπόψη κανένα μηχανισμό
ακτινοβολίας). Τυπικά μεγέθη για τους αστέρες αυτούς είναι μαγνητικό
πεδίο 1012 G, ακτίνα 10 km και περίοδος περιστροφής 0.1 s. Μπορούν να
επιταχύνονται οι κοσμικές ακτίνες στις μαγνητόσφαιρες αυτές;
Δίνεται 1 AU = 1.5 × 1013 cm, 1 pc = 3 × 1018 cm, e = 4.8 × 10-10 cgs, 1 eV
= 1.6 × 10-12 cgs.
Fermi, E. (1949). “On the Origin of the Cosmic Radiation”. Physical Review, 75,
1169.
Longair, M. S., (2011), High Energy Astrophysics. Cambridge University Press
(3rd edition).
Choudhuri, A. R. (1998). The Physics of Fluids and Plasmas: An introduction for
astrophysicists. Cambridge University Press.
Chiuderi, C. & Einaudi, G. (eds.) (1996). Plasma Astrophysics. Springer.
Jackson, J. D. (1998). Classical Electrodynamics. John Wiley & Sons Inc.
Το φαινόμενο των εκροών από αστρικά αντικείμενα - άστρα και γαλαξίες - είναι πολύ συχνό. Πλήθος κατηγοριών κοσμικών αντικειμένων χάνουν μάζα με μορφή ανέμου και μαζί μ΄ αυτόν ενέργεια και στροφορμή.
Πολλές από τις εκροές έχουν τη μορφή πίδακα πλάσματος, εστιασμένης δηλαδή εκροής που εκτείνεται σε πολύ μεγάλες αποστάσεις από το κεντρικό σώμα, τα jets. Ειδικά θα μας απασχολήσουν μαγνητισμένες σχετικιστικές εκροές, οι οποίες είναι πλέον κοινά αποδεκτό ότι δημιουργούνται σε περιβάλλοντα συμπαγών σωμάτων, όπως μελανές οπές και αστέρες νετρονίων. Στο παρόν κεφάλαιο θα εξετάσουμε το πώς μπορούμε να περιγράψουμε γενικά μια μαγνητισμένη εκροή με σκοπό να καταλάβουμε πώς μπορεί να επιταχύνεται και να αποκτά τις σχετικιστικές ταχύτητες που παρατηρούμε.
Μιλώντας για ταχύτητα ή επιτάχυνση της εκροής εννοούμε τη μακροσκοπική ταχύτητα ή επιτάχυνση που καθορίζεται από τη δυναμική. Οι μεμονωμένες κινήσεις σωματίων στο κινούμενο μαζί με τη ροή σύστημα αναφοράς είναι κάτι διαφορετικό· τις κινήσεις αυτές τις λαμβάνουμε υπόψη μέσω των θερμοδυναμικών μεγεθών εσωτερική ενέργεια και θερμοκρασία.
Για να κρατήσουμε τη μελέτη όσο γίνεται απλούστερη δεν θα λάβουμε υπόψη γενική σχετικότητα παρά μόνο ειδική, δηλ. θα θεωρήσουμε ότι ο χωρόχρονος είναι επίπεδος. Επίσης θα μελετήσουμε μόνο ομαλές ροές οι οποίες δεν περιέχουν ασυνέχειες. Οι τελευταίες προκύπτουν όταν μια ομαλή ροή διαταραχθεί (π.χ. λόγω αλληλεπίδρασης με τον μεσοαστρικό χώρο), όπως εξετάσαμε στο κεφάλαιο 7.
Μια μαγνητισμένη ροή πλάσματος περιγράφεται από:
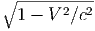 . Στην πραγματικότητα
οι πληθυσμοί θετικών και αρνητικών φορτίων κινούνται με ελάχιστα
διαφορετικές ταχύτητες V + και V -, οι οποίες είναι πολύ κοντά στη
μακροσκοπική ταχύτητα V .
. Στην πραγματικότητα
οι πληθυσμοί θετικών και αρνητικών φορτίων κινούνται με ελάχιστα
διαφορετικές ταχύτητες V + και V -, οι οποίες είναι πολύ κοντά στη
μακροσκοπική ταχύτητα V .
Οι παραπάνω φυσικές ποσότητες συνδέονται μεταξύ τους με νόμους που περιγράφονται στη συνέχεια.
Το ηλεκτρικό και μαγνητικό πεδίο συνδέονται με την πυκνότητα ρεύματος και φορτίου σύμφωνα με τις τέσσερις εξισώσεις του Maxwell . Συγκεκριμένα:
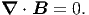 | (9.1) |
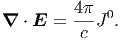 | (9.2) |
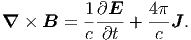 | (9.3) |
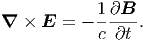 | (9.4) |
Πρέπει να τονιστεί ότι λόγω της κίνησης της ροής, οι κινήσεις των φορτίων συνεπάγονται την ύπαρξη πυκνότητας ρεύματος και φορτίου. Δεν είναι σωστό όμως να θεωρούμε αυτές τις πυκνότητες υπεύθυνες για τη δημιουργία των πεδίων E και B. Στην πραγματικότητα μάλλον το αντίθετο συμβαίνει: υπάρχουν άφθονα φορτία μέσα στη ροή και η ύπαρξη των πεδίων τα κινεί ώστε να «δημιουργήσουν» J και J0∕c. Σε κάθε περίπτωση, ασφαλέστερο είναι να θεωρούμε απλά ότι τα E και B συνυπάρχουν με κάποια J και J0∕c. (Το ότι η πυκνότητα φορτίου και ρεύματος δεν είναι γενικά μηδέν σημαίνει ότι τόσο οι πυκνότητες θετικών και αρνητικών φορτίων, όσο και οι ταχύτητές τους δεν είναι ακριβώς ίσες μεταξύ τους.)
Ο νόμος του Ohm συνδέει την πυκνότητα ρεύματος με το ηλεκτρομαγνητικό πεδίο μέσω της ειδικής αγωγιμότητας Eco = Jco∕σc, όπου Eco το ηλεκτρικό πεδίο και Jco η πυκνότητα ρεύματος στο σύστημα αναφοράς που κινείται με το ρευστό. Στα πλαίσια της ιδεατής μαγνητοϋδροδυναμικής, η αγωγιμότητα των πλασμάτων που μελετούμε είναι τόσο υψηλή (σε σχέση με τις χρονικές κλίμακες που εξετάζουμε), ώστε να ισχύει Eco = 0. Χρησιμοποιώντας μετασχηματισμούς Lorentz του ηλεκτρομαγνητικού πεδίου βρίσκουμε1
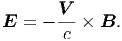 | (9.5) |
Θεωρώντας ιδανικό αέριο, ισοτροπικό στο σύστημα της ροής, η θερμοκρασία είναι μια γνωστή συνάρτηση της πίεσης και της πυκνότητας. Συγκεκριμένα, P = (n+ + n-)kBT. Αν έχουμε ηλεκτρόνια-πρωτόνια (ep πλάσμα) τότε n+ + n- ≈ 2ρ0∕mp, ενώ αν έχουμε ηλεκτρόνια-ποζιτρόνια (e± πλάσμα), n+ + n- = ρ0∕me.
Σύμφωνα με την κινητική θεωρία των αερίων, αν έχουμε ένα αέριο με f βαθμούς ελευθερίας (f = 3 για μονατομικό αέριο), η εσωτερική ενέργεια για κάθε σωμάτιο είναι (f∕2)kBT. ΄Ετσι, η εσωτερική ενέργεια ανά μονάδα μάζας είναι e = (f∕2)(P∕ρ0). Ορίζοντας τον πολυτροπικό δείκτη ως Γ = 1 + 2∕f έχουμε
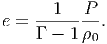 | (9.6) |
Το παραπάνω αποτέλεσμα ισχύει για μη σχετικιστικές θερμικές κινήσεις (δηλ. όταν η
ταχύτητα κάθε σωματίου στο σύστημα της ροής είναι « c), όπου mc2 » k
BT. Σε
σχετικιστικές θερμοκρασίες kBT » mc2, οπότε η ενέργεια κάθε σωματίου είναι
ανάλογη της ορμής του 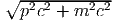 ≈ pc, ένα μονατομικό αέριο συμπεριφέρεται
σαν αέριο φωτονίων με e = 3P∕ρ0. Βλέπουμε ότι η σχέση (9.6) εξακολουθεί να
ισχύει, αυτή τη φορά όμως με Γ = 4∕3 (αυτή η τιμή του Γ δεν σχετίζεται με βαθμούς
ελευθερίας).
≈ pc, ένα μονατομικό αέριο συμπεριφέρεται
σαν αέριο φωτονίων με e = 3P∕ρ0. Βλέπουμε ότι η σχέση (9.6) εξακολουθεί να
ισχύει, αυτή τη φορά όμως με Γ = 4∕3 (αυτή η τιμή του Γ δεν σχετίζεται με βαθμούς
ελευθερίας).
Είναι χρήσιμο να ορίσουμε την ενθαλπία ανά μονάδα μάζας, διαιρεμένη με c2 ώστε να γίνει αδιάστατη. Αφού η ενθαλπία είναι το άθροισμα της ενέργειας ηρεμίας, της εσωτερικής ενέργειας και του γινομένου πίεση επί όγκο, το μέγεθος αυτό είναι ξ = 1 + (e + P∕ρ0)∕c2, ή
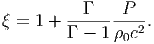 | (9.7) |
΄Οταν οι θερμοκρασίες είναι μη σχετικιστικές ο λόγος P∕ρ0c2 ∝ k BT∕mc2 « 1, και άρα ξ ≈ 1.
Μια ποσότητα του αερίου μάζας δm καταλαμβάνει όγκο δm∕ρ0 στο σύστημα ηρεμίας του. Αν η θερμότητα που παρέχεται σ΄ αυτή τη μάζα είναι δQ, τότε ο πρώτος νόμος της θερμοδυναμικής (ο οποίος εκφράζει τη διατήρηση της ενέργειας) γράφεται d(δQ) = d(eδm) + Pd(δm∕ρ0). Σε περίπτωση αδιαβατικής μεταβολής δQ = 0 και έχουμε de + Pd(1∕ρ0) = 0, ή de∕dt + Pd(1∕ρ0)∕dt = 0. Η μεταβολή κάθε φυσικής ποσότητας που αφορά το ρευστό οφείλεται σε δύο παράγοντες: (1) στην τυχούσα άμεση χρονοεξάρτηση των ποσοτήτων και (2) στην κίνηση του ρευστού. Μαθηματικά αυτό εκφράζεται σαν
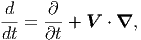
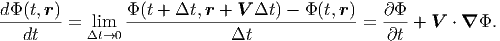
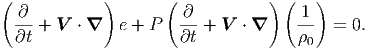
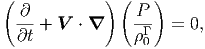 | (9.8) |
που δείχνει ότι η ποσότητα P∕ρ0Γ πρέπει να μένει αμετάβλητη καθώς το πλάσμα κινείται.
΄Εστω ένας όγκος δτ ο οποίος περικλείεται από την κλειστή επιφάνεια S. Αν δm είναι η μάζα του αερίου που υπάρχει σ΄ αυτόν τον όγκο, τότε -d(δm)∕dt = -∂(δm)∕∂t είναι ο ρυθμός ελάττωσης της μάζας μέσα στον όγκο δτ. Λόγω διατήρησης της μάζας, αυτός ο ρυθμός ελάττωσης ισούται με τη ροή μάζας η οποία περνά την επιφάνεια S, η οποία είναι ∯ (γρ0)V ⋅ dS = ∭ ∇⋅ (γρ0V )dτ, όπου γρ0 είναι η πυκνότητα μάζας στο σύστημα του εργαστηρίου. Γράφοντας δm = ∭ γρ0dτ και εξισώνοντας τις δυο εκφράσεις έχουμε τελικά
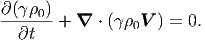 | (9.9) |
Οι δυνάμεις που ασκούνται στο ρευστό ανά μονάδα του όγκου του είναι:
Στην περίπτωση μη σχετικιστικών θερμοκρασιών, το άθροισμα αυτών των δυνάμεων (μαζί με τυχόν άλλες εξωτερικές δυνάμεις) ήταν ίσο με τη δύναμη αδράνειας ανά όγκο, η οποία γράφεται γρ0d(γV )∕dt = γρ0(∂∕∂t + V ⋅∇)(γV ). Ο γενικός τύπος είναι λίγο διαφορετικός: το άθροισμα ισούται με γρ0d(ξγV )∕dt = γρ0(∂∕∂t + V ⋅∇)(ξγV ) (η απόδειξη γίνεται με τη χρήση του τανυστή ενέργειας-ορμής2 ). ΄Ετσι η εξίσωση ορμής είναι
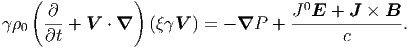 | (9.10) |
Αφού οι εκροές που θα μας απασχολήσουν προέρχονται από περιστρεφόμενα κοσμικά αντικείμενα, μια πρώτη απλούστευση γίνεται αν υποθέσουμε αξισυμμετρία. Δηλ. σε σφαιρικές (r,θ,ϕ) ή κυλινδρικές (z,ϖ,ϕ) συντεταγμένες, με τον άξονα z άξονα περιστροφής, ισχύει ∂∕∂ϕ = 0. Επίσης, όταν μελετούμε τις ροές σε χρονικές κλίμακες πολύ μικρότερες από αυτές που χρειάζονται για να αλλάξουν εντελώς μορφή, μπορούμε να υποθέσουμε χρονοανεξαρτησία ∂∕∂t = 0. Τότε, όλες οι άγνωστες ποσότητες εξαρτώνται από ένα ζευγάρι μεταβλητών, των (z,ϖ) ή (r,θ) ανάλογα με την επιλογή συντεταγμένων.
΄Οπως θα δούμε στη συνέχεια, σ΄ αυτήν την περίπτωση το πρόβλημα σχετικά απλουστεύεται, διότι είναι δυνατή η μερική ολοκλήρωση των περισσότερων από τις προηγούμενες εξισώσεις. Τα ολοκληρώματα κίνησης περιέχουν σημαντικές πληροφορίες για το πώς εξελίσσεται η ροή και η μελέτη τους μας δίνει μια ευκαιρία να κατανοήσουμε καλύτερα το μέχρι τώρα πολύπλοκο σύστημα που εξετάζουμε.
Η σημαντικότερη ποσότητα του προβλήματος είναι η συνάρτηση μαγνητικής ροής.
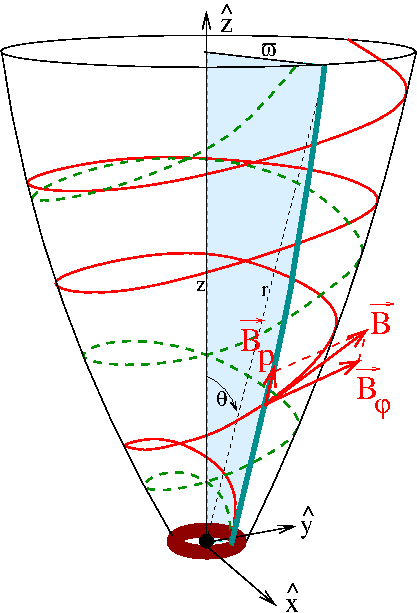
Αρχικά θα ορίσουμε το πολοειδές επίπεδο σαν το επίπεδο (z,ϖ) σε κυλινδρικές (ή [r,θ] σε σφαιρικές) συντεταγμένες, βλ. σχήμα 9.1. ΄Ετσι, αναλύουμε την ταχύτητα σε πολοειδή V p και αζιμουθιακή V ϕ. ΄Ομοια, αναλύουμε το μαγνητικό πεδίο σε πολοειδές Bp και αζιμουθιακό Bϕ.
Η πρώτη εξίσωση Maxwell γίνεται ∇⋅Bp = 0. ΄Αρα υπάρχει συνάρτηση A(ϖ,z) τέτοια ώστε
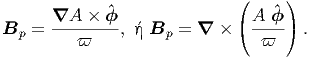 | (9.11) |
Από τη δεύτερη γραφή φαίνεται ότι το A σχετίζεται με το διανυσματικό δυναμικό του πολοειδούς μαγνητικού πεδίου. Εύκολα μπορεί να δειχθεί ότι
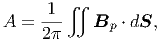 | (9.12) |
συσχετίζοντας τη συνάρτηση A με τη μαγνητική ροή. ΄Αρα η εξίσωση της πολοειδούς μαγνητικής γραμμής (που είναι και η προβολή του B στο πολοειδές επίπεδο) είναι A = σταθ., βλ. σχήμα 9.1.
Η εξίσωση του Faraday, στην περίπτωση που το μαγνητικό πεδίο δεν μεταβάλλεται
χρονικά, δίνει ότι το ηλεκτρικό πεδίο προέρχεται από βαθμωτό δυναμικό E = -∇Φ.
Λόγω της αξισυμμετρίας, Eϕ = 0. ΄Ομως ο νόμος του Ohm (9.5) δίνει σ΄ αυτήν την
περίπτωση (V ×B) ⋅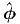 = 0 ⇔ (V p ×Bp) ⋅
= 0 ⇔ (V p ×Bp) ⋅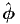 = 0, κάτι που σημαίνει ότι τα V p και
Bp είναι παράλληλα. Αυτό είναι πολύ σημαντικό συμπέρασμα και σημαίνει ότι η ροή
ακολουθεί το μαγνητικό πεδίο στο πολοειδές επίπεδο (αν και στις τρεις διαστάσεις η
γραμμή ροή δεν ταυτίζεται με τη γραμμή του μαγνητικού πεδίου όπως δείχνει το
σχήμα 9.1).
= 0, κάτι που σημαίνει ότι τα V p και
Bp είναι παράλληλα. Αυτό είναι πολύ σημαντικό συμπέρασμα και σημαίνει ότι η ροή
ακολουθεί το μαγνητικό πεδίο στο πολοειδές επίπεδο (αν και στις τρεις διαστάσεις η
γραμμή ροή δεν ταυτίζεται με τη γραμμή του μαγνητικού πεδίου όπως δείχνει το
σχήμα 9.1).
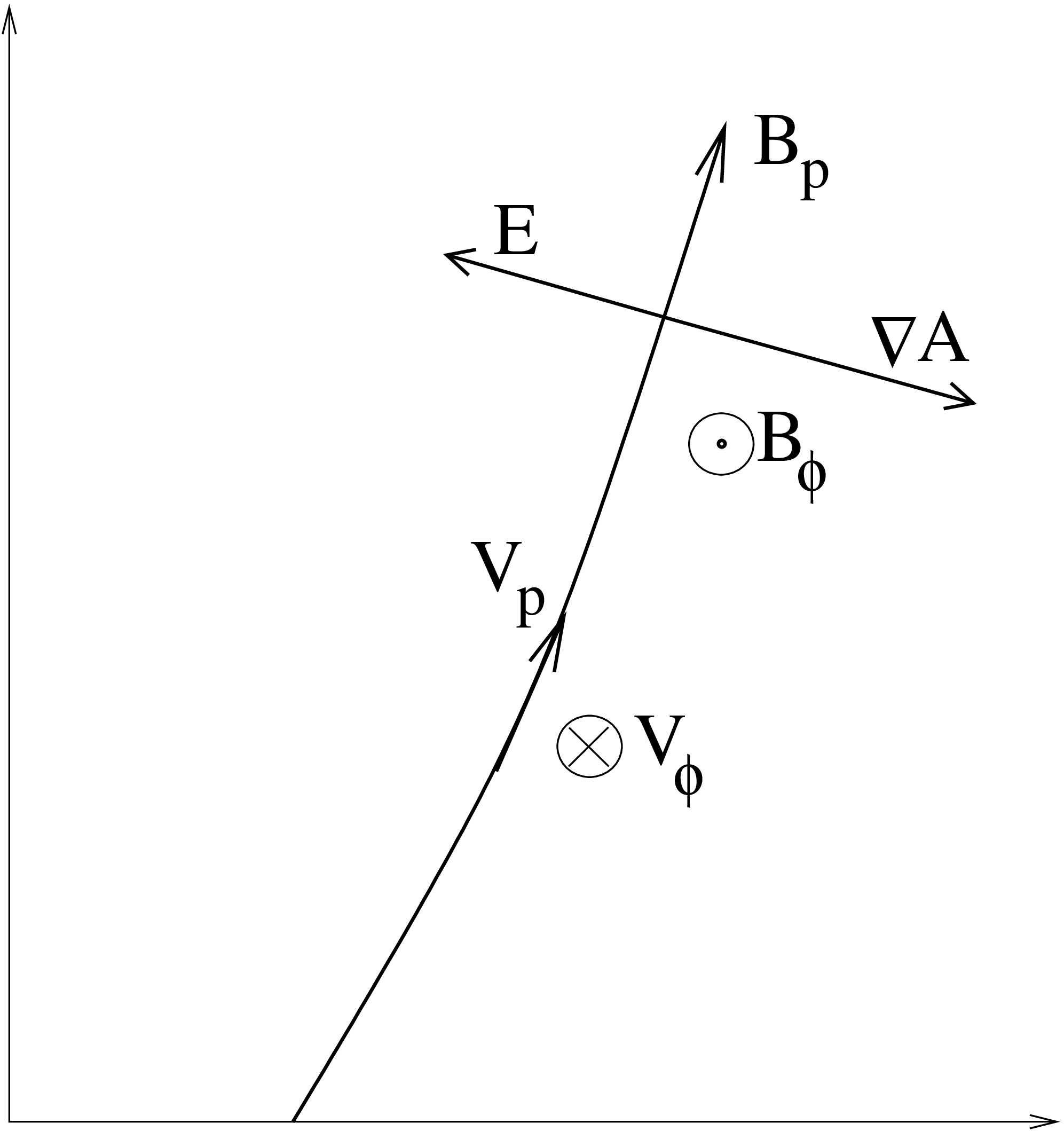
Αφού τα V p, Bp είναι παράλληλα, υπάρχουν συναρτήσεις ΨA και Ω τέτοιες ώστε
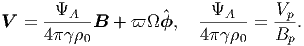 | (9.13) |
Αντικαθιστώντας την προηγούμενη σχέση στον νόμο του Ohm (9.5) έχουμε:
E = -(ϖΩ∕c)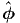 ×Bp. Χρησιμοποιώντας την εξίσωση (9.11) βρίσκουμε πως το
ηλεκτρικό πεδίο είναι
×Bp. Χρησιμοποιώντας την εξίσωση (9.11) βρίσκουμε πως το
ηλεκτρικό πεδίο είναι
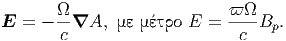 | (9.14) |
Παρατηρήστε ότι η διεύθυνση του E είναι κάθετη στις δυναμικές γραμμές του μαγνητικού πεδίου (που όπως είπαμε έχουν προβολή πάνω στο πολοειδές επίπεδο A = σταθ.). Η φορά του E είναι αντίθετη από τη φορά του ∇A, άρα το ηλεκτρικό πεδίο «κοιτάζει προς τον άξονα περιστροφής», όπως δείχνει το σχήμα 9.2.
Χρησιμοποιώντας την εξίσωση (9.14), ο νόμος του Faraday (9.4) δίνει ∇ × (Ω∇A) = 0 ⇔ ∇Ω ×∇A = 0. Αυτό σημαίνει ότι Ω = Ω(A), δηλ. το Ω είναι μια σταθερά κίνησης. Από γραμμή σε γραμμή το Ω μπορεί να είναι διαφορετικό, αλλά αφού το ρευστό κινείται πάνω στις γραμμές A = σταθ, το Ω μένει σταθερό κατά τη διάρκεια της κίνησης κάθε μέρους της ροής.
Αν κοντά στο κεντρικό σώμα απ΄ όπου ξεκίνησε η ροή η πυκνότητα είναι αρκούντως μεγάλη, βλέπουμε από την εξίσωση (9.13) ότι V ϕ ≈ ϖΩ. Δηλ. Ω είναι η γωνιακή ταχύτητα του ρευστού κοντά στη βάση της εκροής. Πιο μακρυά πάντως ο άλλος όρος της αζιμουθιακής ταχύτητας δεν είναι πια αμελητέος και το προηγούμενο συμπέρασμα δεν ισχύει.
Αντικαθιστώντας την εξίσωση (9.13) στην εξίσωση συνέχειας (9.9), και αφού ∇ ⋅ B = 0, προκύπτει ότι Bp ⋅∇ΨA = 0. Δηλ. η παράγωγος του ΨA κατά μήκος της πολοειδούς δυναμικής γραμμής του B είναι μηδέν. Αυτό σημαίνει ότι ΨA = ΨA(A), οπότε το ΨA είναι άλλη μια σταθερά κίνησης. Από την εξίσωση (9.13), ΨA = 2(γρ0V pδS)∕(BpδS∕2π). Ο παρονομαστής είναι η μαγνητική ροή (βλ. εξίσωση 9.12), ενώ ο αριθμητής είναι η ροή μάζας (ο παράγοντας 2 υπολογίζει τη ροή μάζας και από τα δύο ημισφαίρια). Δηλ. η σταθερά κίνησης ΨA παριστάνει τον λόγο της ροής μάζας προς τη μαγνητική ροή, και δηλώνει ότι αυτός μένει σταθερός κατά τη διάρκεια της κίνησης (κάτι που θα έπρεπε να το περιμένουμε αφού V p ∥ Bp).
Η εξίσωση (9.8) ολοκληρώνεται αμέσως και δίνει P∕ρ0Γ = Q(A). Αφού η εντροπία ανά μονάδα μάζας είναι συνάρτηση του P∕ρ0Γ, η παραπάνω σχέση δηλώνει ότι η εντροπία μένει σταθερή κατά την κίνηση του ρευστού όταν δεν υπάρχει θερμότητα.
Αφού έχουμε υποθέσει αξισυμμετρία, πρέπει να υπάρχει κάποιο ολοκλήρωμα
στροφορμής. Πράγματι, η 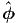 συνιστώσα της εξίσωσης της ορμής (9.10)
ολοκληρώνεται και δίνει
συνιστώσα της εξίσωσης της ορμής (9.10)
ολοκληρώνεται και δίνει
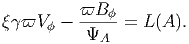 | (9.15) |
Ο πρώτος όρος αντιστοιχεί στη στροφορμή του υλικού ανά μονάδα μάζας, ενώ ο δεύτερος στη στροφορμή του ηλεκτρομαγνητικού πεδίου. Βλέπουμε ότι μόνο η ολική στροφορμή μένει σταθερή· μπορούμε όμως να έχουμε μετακίνηση στροφορμής από το πεδίο στην ύλη και αντίστροφα. ΄Οταν ο όρος που αντιστοιχεί στο πεδίο είναι αμελητέος, τότε προκύπτει ότι ξγV ϕ ∝ 1∕ϖ, το οποίο ανάγεται στο γνωστό μας από μη σχετικιστικές κινήσεις αποτέλεσμα V ϕ ∝ 1∕ϖ.
Το ολοκλήρωμα της ενέργειας προκύπτει αν προβάλλουμε την εξίσωση της ορμής πάνω στην κίνηση, πολλαπλασιάζοντας δηλ. την εξίσωση (9.10) με V . Το αποτέλεσμα είναι
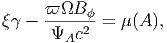 | (9.16) |
και εκφράζει τη διατήρηση του λόγου της ροής ενέργειας προς ροή μάζας (διαιρούμενο με c2 ώστε να γίνει αδιάστατο). Ο δεύτερος όρος αφορά την ενέργεια του ηλεκτρομαγνητικού πεδίου και πρέπει να σχετίζεται με τη ροή Poynting. Πράγματι, όπως θα δείξουμε στη συνέχεια η ροή ενέργειας του ηλεκτρομαγνητικού πεδίου (c∕4π)E × B χωρίζεται σε δύο μέρη. Το μέρος (c∕4π)E × Bp έχει αζιμουθιακή διεύθυνση και άρα περιγράφει ενέργεια που δεν μπορεί να διαφύγει. Αντίθετα το μέρος (c∕4π)E ×Bϕ έχει τη διεύθυνση της ταχύτητας, και φορά προς τα έξω αν Bϕ < 0. Το μέτρο του είναι (c∕4π)E|Bϕ| = (c∕4π)(ϖΩ∕c)Bp|Bϕ|, όπου χρησιμοποιήσαμε την εξίσωση (9.14). Επομένως αν διαιρέσουμε με τη ροή μάζας επί c2, δηλ. με (γρ 0)V pc2, και χρησιμοποιήσουμε ότι V p∕Bp = ΨA∕4πγρ0 (βλ. εξίσωση [9.13]), παίρνουμε ϖΩ|Bϕ|∕ΨAc2, δηλ. ακριβώς το δεύτερο μέρος της εξίσωσης (9.16). Ο πρώτος όρος της εξίσωσης (9.16) είναι η ροή ενέργειας που αφορά την ύλη (ροή κινητικής ενέργειας και ενθαλπίας, συμπεριλαμβανομένης και της ενέργειας ηρεμίας) προς τη ροή μάζας (προς c2).
Ανάλογα με το αν στο άθροισμα της εξίσωσης (9.16) κυριαρχεί ο όρος της ύλης (ξγ) ή ο όρος του ηλεκτρομαγνητικού πεδίου (ϖΩ|Bϕ|∕ΨAc2), ονομάζουμε τη ροή Poynting-κυριαρχούμενη (οπότε ξγ « ϖΩ|Bϕ|∕ΨAc2 και ϖΩ|B ϕ|∕ΨAc2 ≈ μ) ή ύλο-κυριαρχούμενη (τότε ξγ » ϖΩ|Bϕ|∕ΨAc2 και ξγ ≈ μ). Βέβαια μπορούμε να έχουμε γενικά μια ροή η οποία είναι Poynting-κυριαρχούμενη κοντά στη βάση της αλλά αργότερα γίνεται ύλο-κυριαρχούμενη.
Συνοψίζοντας, έχουμε βρει ότι η πολοειδής δυναμική γραμμή ταυτίζεται με την πολοειδή γραμμή ροής και έχει εξίσωση A = σταθ. Η συνάρτηση A είναι ανάλογη της μαγνητικής ροής (ο άξονας περιστροφής είναι A = 0). Συναρτήσει του A, έχουμε για το πολοειδές μαγνητικό πεδίο
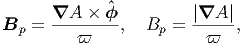 | (9.17) |
και για το ηλεκτρικό πεδίο
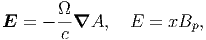 | (9.18) |
όπου ορίσαμε την κυλινδρική απόσταση σε μονάδες της ακτίνας του «κυλίνδρου φωτός»
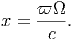 | (9.19) |
Επίσης βρήκαμε το ολοκλήρωμα ΨA, συναρτήσει του οποίου η πολοειδής ταχύτητα γράφεται
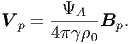 | (9.20) |
Το ότι η κίνηση είναι αδιαβατική εκφράζεται από τη σχέση
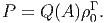 | (9.21) |
Βρήκαμε ακόμα τρία ολοκληρώματα, τα Ω, L και μ, τα οποία συσχετίζουν τα μεγέθη V ϕ, Bϕ, και γ σύμφωνα με τις σχέσεις
Οι σχέσεις (9.22–9.24) μπορούν να λυθούν ως προς V ϕ, Bϕ, και γ. Τα αποτελέσματα είναι:
όπου ορίσαμε την ποσότητα
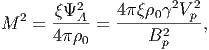 | (9.28) |
και την
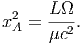 | (9.29) |
Παρατηρήστε ότι Bϕ < 0 όπως περιμέναμε,3 κάτι που αντιστοιχεί σε εκροή Poynting (E × B) ⋅ V p > 0. ΄Οπως βλέπουμε οι παρονομαστές στις εξισώσεις (9.25–9.27) μηδενίζονται όταν M2 + x2 = 1. Η επιφάνεια στην οποία αυτό συμβαίνει λέγεται επιφάνεια Alfvιn.4 Για να ορίζονται οι ποσότητες στις εξισώσεις (9.25–9.27) πρέπει να μηδενίζονται ταυτόχρονα και οι αριθμητές, δηλ. xA είναι η τιμή του x στην επιφάνεια Alfvιn.
Κοντά στη βάση μιας εκροής η οποία ξεκινά από μικρές αποστάσεις τέτοιες ώστε x « 1, και με μεγάλη πυκνότητα ώστε M « 1 (το τελευταίο ισοδυναμεί με ισχυρό πολοειδές μαγνητικό πεδίο σύμφωνα με τη δεύτερη των εξισώσεων [9.28]), η ύλη περιστρέφεται με γωνιακή ταχύτητα Ω. Αυτό προκύπτει από την εξίσωση (9.22) η οποία γίνεται V ϕ ≈ ϖΩ (ή από την εξίσωση [9.27] για M « 1). Γράφοντας την εξίσωση (9.22) σαν
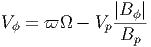 | (9.30) |
(απαλείψαμε το ΨA χρησιμοποιώντας την εξίσωση [9.20]) φαίνεται ότι Bp ≳|Bϕ|, δηλ. το πολοειδές μαγνητικό πεδίο είναι η σημαντικότερη συνιστώσα στην περιοχή M2 + x2 < 1 πριν την επιφάνεια Alfvιn.
Καθώς η ύλη προχωρά σε μεγαλύτερες κυλινδρικές αποστάσεις, κάποια στιγμή θα γίνει M2 + x2 = 1 και αργότερα M2 + x2 > 1. Στην περιοχή M2 + x2 > 1 μετά την επιφάνεια Alfvιn δεν ισχύει πια η ισοπεριστροφή V ϕ ≈ ϖΩ. Μάλιστα σε αρκετά μεγάλες αποστάσεις είναι V ϕ « ϖΩ, οπότε η εξίσωση (9.30) συνεπάγεται |Bϕ|≈ (ϖΩ∕V p)Bp ≈ xBp. ΄Αμεση συνέπεια είναι ότι το ηλεκτρικό πεδίο είναι συγκρίσιμο με το |Bϕ| (αφού E = xBp σύμφωνα με την εξίσωση [9.18]).
΄Οπως είδαμε στα προηγούμενα μπορέσαμε να εκφράσουμε όλες τις φυσικές ποσότητες του προβλήματος σαν συνάρτηση των αγνώστων συναρτήσεων M και A (και των ολοκληρωμάτων τα οποία είναι συναρτήσεις του A). Το πρόβλημα λοιπόν έχει αναχθεί στο να βρούμε αυτές τις δύο συναρτήσεις. Οι δύο εξισώσεις που δεν έχουμε ολοκληρώσει και οι οποίες πρέπει να λυθούν ως προς M και A είναι οι εξίσωση Bernoulli και η εγκάρσια συνιστώσα της εξίσωσης ορμής.
Αν αντικαταστήσουμε στην ταυτότητα γ2 = 1 + γ2V p2∕c2 + γ2V ϕ2∕c2 όλες τις ποσότητες όπως δίνονται σαν συναρτήσεις των M και A, έχουμε την εξίσωση Bernoulli. Η εξίσωση αυτή είναι αλγεβρική και μπορεί να ιδωθεί σαν να δίνει το M συναρτήσει του A και της παραγώγου του |∇A|.
Η μόνη εξίσωση που έμεινε να ολοκληρωθεί είναι η προβολή της εξίσωσης της ορμής κάθετα στην πολοειδή γραμμή, δηλ. η προβολή της εξίσωσης (9.10) πάνω στο ∇A. Η εξίσωση αυτή καθορίζει το σχήμα της πολοειδούς γραμμής. Η σχέση που προκύπτει είναι μια πολύπλοκη και εξαιρετικά μη γραμμική διαφορική εξίσωση δεύτερης τάξης με μόνο άγνωστο το A. Η λύση της με αναλυτικούς ή υπολογιστικούς τρόπους είναι αντικείμενο ερευνητικής προσπάθειας.
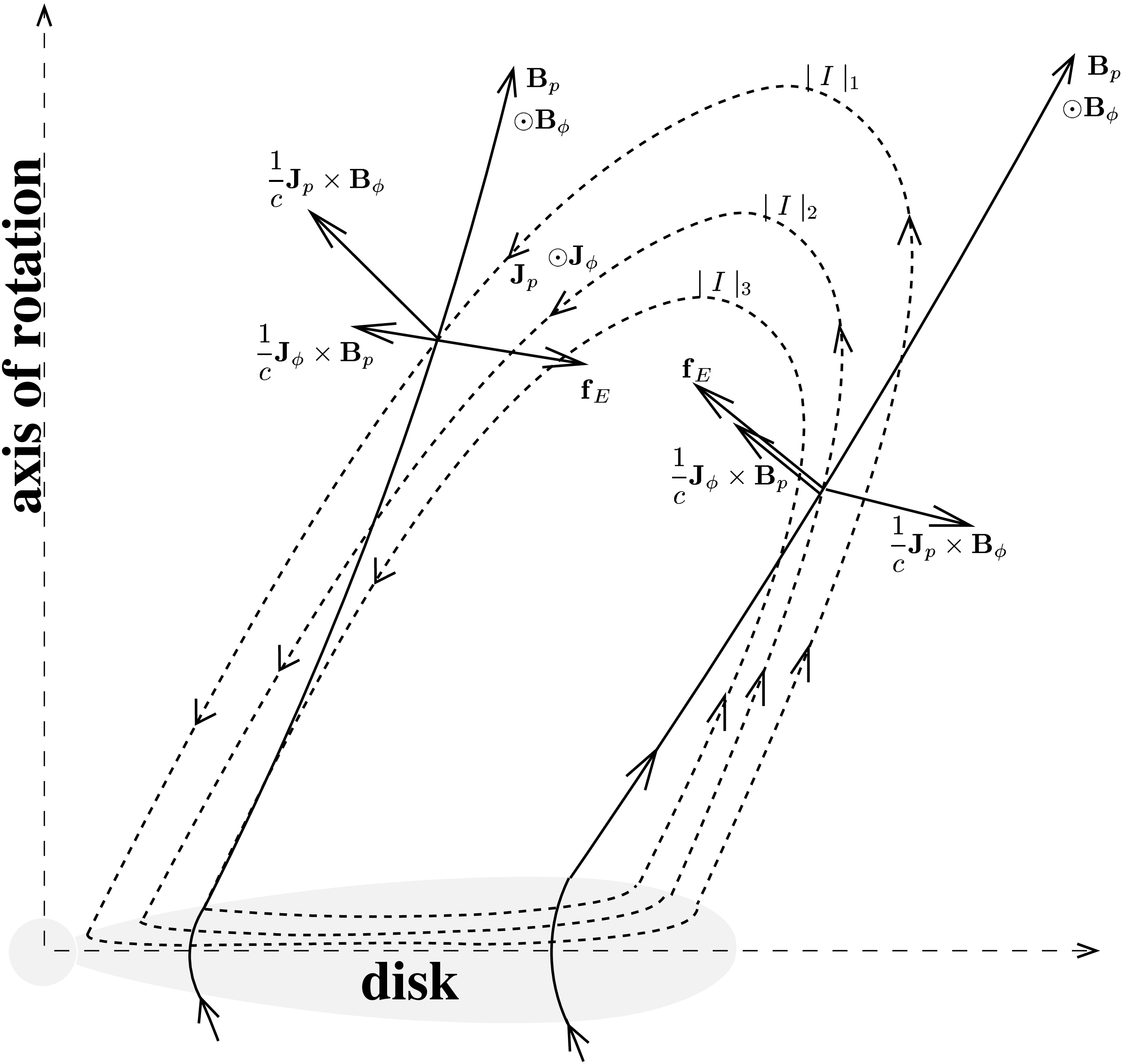
Ας προσπαθήσουμε να καταλάβουμε ποιες είναι οι δυνάμεις που ασκούνται στη ροή κατά την κίνησή της και τι αποτέλεσμα έχουν. Η εξίσωση (9.10) μπορεί να γραφεί σαν το άθροισμα των επόμενων όρων:
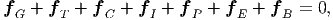

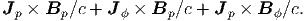
Αν γράψουμε
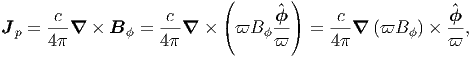
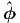 ∕ϖ συμπεραίνουμε ότι οι γραμμές του
πολοειδούς ρεύματος Jp έχουν εξίσωση ϖBϕ = σταθ. Κάθε γραμμή ϖBϕ = σταθ.
περικλείει σταθερό συνολικό ρεύμα I = ∫
∫
Jp ⋅ dS = (c∕2)ϖBϕ, όπως δείχνει το
σχήμα 9.3. Η δύναμη Jp ×Bϕ∕c βρίσκεται πάνω στο πολοειδές επίπεδο και είναι
κάθετη στη γραμμή ρεύματος όπως φαίνεται στο σχήμα 9.3. Η δύναμη αυτή έχει δύο
συνιστώσες: μία παράλληλα στη ροή (δηλ. παράλληλα στην V p), και μία κάθετα
στη ροή. Η πρώτη, όπως βλέπουμε στο σχήμα 9.3 επιταχύνει τη ροή. Το
αποτέλεσμα της δεύτερης εξαρτάται από το αν η ροή βρίσκεται κοντά στον
άξονα περιστροφής (αριστερή γραμμή Bp στο σχήμα 9.3 όπου J∥ < 0) ή
μακρυά (δεξιά γραμμή Bp στο σχήμα 9.3 όπου J∥ > 0). Κοντά στον άξονα
περιστροφής όπου μας ενδιαφέρει περισσότερο να μελετήσουμε τη ροή και
να συγκρίνουμε με τις παρατηρήσεις εστιασμένων πιδάκων πλάσματος, η
δύναμη αυτή εστιάζει τη ροή, δηλ. προσπαθεί να την σπρώξει προς τον άξονα
συμμετρίας.5
Η εξήγηση της παρατηρούμενης επιτάχυνσης και εστίασης αστροφυσικών εκροών με
βάση αυτήν την απλή εικόνα είναι μια από τις επιτυχίες της θεωρίας της
μαγνητοϋδροδυναμικής, αν και οι ποσοτικοί υπολογισμοί είναι αντικείμενο έρευνας
ακόμα και στις μέρες μας.
∕ϖ συμπεραίνουμε ότι οι γραμμές του
πολοειδούς ρεύματος Jp έχουν εξίσωση ϖBϕ = σταθ. Κάθε γραμμή ϖBϕ = σταθ.
περικλείει σταθερό συνολικό ρεύμα I = ∫
∫
Jp ⋅ dS = (c∕2)ϖBϕ, όπως δείχνει το
σχήμα 9.3. Η δύναμη Jp ×Bϕ∕c βρίσκεται πάνω στο πολοειδές επίπεδο και είναι
κάθετη στη γραμμή ρεύματος όπως φαίνεται στο σχήμα 9.3. Η δύναμη αυτή έχει δύο
συνιστώσες: μία παράλληλα στη ροή (δηλ. παράλληλα στην V p), και μία κάθετα
στη ροή. Η πρώτη, όπως βλέπουμε στο σχήμα 9.3 επιταχύνει τη ροή. Το
αποτέλεσμα της δεύτερης εξαρτάται από το αν η ροή βρίσκεται κοντά στον
άξονα περιστροφής (αριστερή γραμμή Bp στο σχήμα 9.3 όπου J∥ < 0) ή
μακρυά (δεξιά γραμμή Bp στο σχήμα 9.3 όπου J∥ > 0). Κοντά στον άξονα
περιστροφής όπου μας ενδιαφέρει περισσότερο να μελετήσουμε τη ροή και
να συγκρίνουμε με τις παρατηρήσεις εστιασμένων πιδάκων πλάσματος, η
δύναμη αυτή εστιάζει τη ροή, δηλ. προσπαθεί να την σπρώξει προς τον άξονα
συμμετρίας.5
Η εξήγηση της παρατηρούμενης επιτάχυνσης και εστίασης αστροφυσικών εκροών με
βάση αυτήν την απλή εικόνα είναι μια από τις επιτυχίες της θεωρίας της
μαγνητοϋδροδυναμικής, αν και οι ποσοτικοί υπολογισμοί είναι αντικείμενο έρευνας
ακόμα και στις μέρες μας.
Στο σχήμα 9.3 φαίνεται επίσης η δύναμη (1∕c)Jϕ ×Bp, η οποία συνεισφέρει κυρίως στην περιοχή πριν την επιφάνεια Alfvιn.
Στην εξίσωση ορμής έχουμε ακόμα δυνάμεις που οφείλονται σε μεταβολή
των θερμοδυναμικών ποσοτήτων P και ξ. Η δύναμη «θερμοκρασίας»
fT = -γ2ρ
0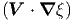 V είναι σημαντική, εφόσον ξ » 1 και έχει συνιστώσα
πάνω στην V p ίση με fT∥ = -γ2ρ
0
V είναι σημαντική, εφόσον ξ » 1 και έχει συνιστώσα
πάνω στην V p ίση με fT∥ = -γ2ρ
0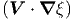 V p η οποία επιταχύνει τη ροή
όταν το πλάσμα κρυώνει (δηλ. το ξ ελαττώνεται). Αν χρησιμοποιήσουμε την
εξίσωση (9.7) και το γεγονός ότι V ⋅∇(P∕ρ0Γ) = 0, μπορούμε να γράψουμε
fT∥ = -γ2V
pV p ⋅∇P∕c2 = (γV
p∕c)2f
P∥, όπου fP∥ = -(V p∕V p) ⋅∇P είναι η
συνιστώσα της δύναμης της πίεσης πάνω στη ροή. Το συμπέρασμα είναι ότι σε
περιπτώσεις σχετικιστικής ροής με γV p∕c » 1 η δύναμη της πίεσης πάνω
στη ροή fP∥ έχει πολύ μικρότερη συνεισφορά από τη δύναμη θερμοκρασίας
fT∥.
V p η οποία επιταχύνει τη ροή
όταν το πλάσμα κρυώνει (δηλ. το ξ ελαττώνεται). Αν χρησιμοποιήσουμε την
εξίσωση (9.7) και το γεγονός ότι V ⋅∇(P∕ρ0Γ) = 0, μπορούμε να γράψουμε
fT∥ = -γ2V
pV p ⋅∇P∕c2 = (γV
p∕c)2f
P∥, όπου fP∥ = -(V p∕V p) ⋅∇P είναι η
συνιστώσα της δύναμης της πίεσης πάνω στη ροή. Το συμπέρασμα είναι ότι σε
περιπτώσεις σχετικιστικής ροής με γV p∕c » 1 η δύναμη της πίεσης πάνω
στη ροή fP∥ έχει πολύ μικρότερη συνεισφορά από τη δύναμη θερμοκρασίας
fT∥.
Η φυγόκεντρος δύναμη fC =  γ2ρ
0ξV ϕ2∕ϖ συνεισφέρει επίσης στην
επιτάχυνση εκεί όπου το V ϕ είναι σημαντικό, δηλ. κοντά στη βάση της ροής πριν την
επιφάνεια Alfvιn. Ο μηχανισμός που βασίζεται στη φυγόκεντρο δύναμη λέγεται
«μαγνητοπεριστροφικός» και είναι πολύ σημαντικός στην επιτάχυνση μη σχετικιστικών
εκροών.6
γ2ρ
0ξV ϕ2∕ϖ συνεισφέρει επίσης στην
επιτάχυνση εκεί όπου το V ϕ είναι σημαντικό, δηλ. κοντά στη βάση της ροής πριν την
επιφάνεια Alfvιn. Ο μηχανισμός που βασίζεται στη φυγόκεντρο δύναμη λέγεται
«μαγνητοπεριστροφικός» και είναι πολύ σημαντικός στην επιτάχυνση μη σχετικιστικών
εκροών.6
(α) Ποια η ενθαλπία (συμπεριλαμβανομένης της ενέργειας ηρεμίας) ανά
μονάδα μάζας (ξc2) μιας ροής ηλεκτρονίων-πρωτονίων; Πώς συνδέεται με τη
θερμοκρασία αν αυτή είναι σχετικιστική ή μη-σχετικιστική;
(β) ΄Ενας πίδακας ενεργού γαλαξιακού πυρήνα παρατηρείται να κινείται
σχετικιστικά, με παράγοντα Lorentz γ = 10. Αν υποθέσουμε ότι έχει
επιταχυνθεί υδροδυναμικά και αποτελείται από ηλεκτρόνια-πρωτόνια, ποια είναι
η απαιτούμενη θερμοκρασία στη βάση του;
Δίνονται οι σταθερές (στο σύστημα cgs ): c = 3 × 1010, k
B = 1.38 × 10-16,
mp = 1.67 × 10-24, m
e = 9.11 × 10-28.
Κοντά σε μελανή οπή μάζας 108M
⊙, περιστρέφεται μια μαγνητισμένη εκροή
ηλεκτρονίων-πρωτονίων στην οποία Bpi = 104G, |B
ϕ|i = 103G. Η εκροή ξεκινά
με γi ~ 1 και Ti = 1010K, και μεταφέρει μάζα με ρυθμό Ṁ = 10-3M
⊙yr-1.
(α) Ποια η ολική ροή ενέργειας προς τη ροή μάζας προς c2 (δηλ. ποιο είναι το
μ);
(β) Ποια τα μέρη του μ που αντιστοιχούν στην ύλη και στο ηλεκτρομαγνητικό
πεδίο; Ποιες οι αντίστοιχες ισχύες;
(γ) Ποιο το μέγιστο γ που μπορεί να αποκτήσει αυτή η ροή;
(δ) Ποια η ολική στροφορμή που εκρέει ανά μονάδα χρόνου; Αρχικά ποιο μέρος
της αντιστοιχεί στην ύλη;
(ε) Αν το σχήμα των δυναμικών γραμμών A = σταθ. είναι τέτοιο ώστε
ασυμπτωτικά να έχουμε ισοκατανομή μεταξύ ενέργειας της ύλης και ενέργειας
του πεδίου, ποιο είναι το γ∞;
(στ) Εκτιμήστε ποια είναι η αρχική πυκνότητα της εκροής.
Θεωρήστε ότι η εκροή εκτείνεται από ϖin = 5rg ως ϖout = 10rg, όπου rg η
ακτίνα Schwarzschild.
Μια εστιασμένη κρύα εκροή κινείται με γ∞ = 15, έχει γωνιακό ημιάνοιγμα ϑ = 3o και μεταφέρει μάζα με ρυθμό Ṁ = 10-3M ⊙yr-1. Αν με κάποιο μηχανισμό το 1% της ασυμπτωτικής κινητικής ενέργειας μετατρέπεται σε ακτινοβολία, ποια θα είναι η ροή της ενέργειας που φτάνει στη γη; Δίνεται απόσταση γης–αντικειμένου = 1 Gpc.
Δείξτε ότι σε γενικές γραμμές το πολοειδές μαγνητικό πεδίο μεταβάλλεται σαν Bp ∝ 1∕ϖ2. Επίσης ότι η πυκνότητα στο σύστημα εργαστηρίου αλλάζει σαν γρ0 ∝ 1∕ϖ2. Στην περίπτωση Poynting-κυριαρχούμενης ροής (ξγ « μ) δείξτε ότι Bϕ ∝ 1∕ϖ, δηλ. το γινόμενο ϖBϕ αλλάζει πολύ αργά.
Σε περίπτωση εστιασμένης ροής με V ϖ « V z, δείξτε ότι ο παράγοντας Lorentz είναι γ ≳ z∕ϖ. (ϒπόδειξη: Συγκρίνετε τα ϖ και ∫ V ϖdt.)
΄Εστω ότι μελετούμε μια υδροδυναμική ροή e± η οποία έχει σχετικιστικές θερμοκρασίες P » ρ0c2.
Δείξτε ότι κοντά στη βάση μιας μαγνητισμένης εκροής είναι ξiγi ≈ μ(1 - xA2). Για μια σχετικιστική εκροή με μ » 1 η οποία κυριαρχείται αρχικά από τη ροή Poynting, δηλ. ξiγi « μ, δείξτε ότι το xA ≈ 1-, δηλ. η επιφάνεια Alfvιn είναι λίγο πριν τον «κύλινδρο φωτός».
(α) Το ολοκλήρωμα της ενέργειας σε μια στάσιμη μαγνητισμένη εκροή είναι
ξγ -ϖΩBϕ∕ΨAc2 = μ. Τι παριστάνουν τα διάφορα σύμβολα και ποια από αυτά
είναι σταθερές της κίνησης; Τι εκφράζει καθένας από τους τρεις όρους της
σχέσης; Συσχετίστε τον δεύτερο όρο με τη ροή Poynting (c∕4π)E ×B.
(β) Γύρω από μια μελανή οπή μάζας 109M
⊙ υπάρχει δίσκος προσαύξησης
που εκτείνεται σε κυλινδρικές αποστάσεις 5rS < ϖ < 6rS και περιστρέφεται
κεπλεριανά. Από την επιφάνεια του δίσκου εκρέει ύλη με ρυθμό Ṁ =
10-3M
⊙yr-1. Αν κοντά στη βάση της εκροής B
p = 104G, |B
ϕ| = 102G, ποιος
ο μέγιστος παράγοντας Lorentz που μπορεί να αποκτήσει η εκροή; (Κοντά στη
βάση της εκροής η ροή ενέργειας είναι κυρίως Poynting.) Ποια η θεωρητικά
μέγιστη λαμπρότητα του jet;
Δίνονται G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g, 1yr= 3 × 107s, και
rS = 2GM∕c2, 4πγρ
0V p = ΨABp, V ϕ = ϖΩ + V pBϕ∕Bp, E = BpϖΩ∕c.
(α) Το ολοκλήρωμα της ενέργειας σε μια στάσιμη μαγνητισμένη εκροή είναι
ξγ - ϖΩBϕ∕ΨAc2 = μ. Τι παριστάνουν τα διάφορα σύμβολα και ποια απ΄ αυτά
είναι σταθερές της κίνησης; Τι εκφράζει καθένας από τους τρεις όρους της
σχέσης; Συσχετίστε τον δεύτερο όρο με τη ροή Poynting (c∕4π)E ×B.
(β) ΄Εστω ότι μελετάμε μια κρύα, ισχυρά σχετικιστική εκροή, στην οποία
η περιστροφική ταχύτητα μπορεί να θεωρηθεί αμελητέα (V ϕ « ϖΩ).
Χρησιμοποιώντας το ολοκλήρωμα ενέργειας δείξτε ότι ο παράγοντας Lorentz
εξαρτάται από το σχήμα των πολοειδών μαγνητικών γραμμών, μέσω της
συνάρτησης f = Bpϖ2∕A.
Δίνονται οι σχέσεις V p = ΨABp∕(4πγρ0), V ϕ = ΨABϕ∕(4πγρ0) + ϖΩ.
(γ) Πώς πρέπει να μεταβάλλεται η συνάρτηση f = Bpϖ2∕A για να έχουμε
επιτάχυνση; Αν ασυμπτωτικά το πεδίο έχει μονοπολική μορφή (Bp ∝ 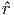 ∕r2),
ποια η ασυμπτωτική τιμή του παράγοντα Lorentz και ποιος ο λόγος της ροής
Poynting προς την ολική ροή ενέργειας; (Τα αποτελέσματά σας πρέπει να είναι
συναρτήσεις των ολοκληρωμάτων κίνησης A, Ω, ΨA, μ.)
∕r2),
ποια η ασυμπτωτική τιμή του παράγοντα Lorentz και ποιος ο λόγος της ροής
Poynting προς την ολική ροή ενέργειας; (Τα αποτελέσματά σας πρέπει να είναι
συναρτήσεις των ολοκληρωμάτων κίνησης A, Ω, ΨA, μ.)
Δίνεται η σχέση 2πA = ∫
∫
Bp ⋅ dS.
Μία έκλαμψη ακτινοβολίας γ (Gamma-Ray Burst) διαρκεί Δt = 10s και
ακτινοβολεί ενέργεια E = 1051ergs.
(α) Αν η ενέργεια αυτή, πριν ακτινοβοληθεί, ήταν κινητική ενέργεια εκροής με
παράγοντα Lorentz γ = 100, ποια η μάζα της εκροής και ποιος ο ρυθμός Ṁ;
(β) ΄Εστω ότι αυτή η κινητική ενέργεια είναι αποτέλεσμα μαγνητικής
επιτάχυνσης σε μια εκροή που προέρχεται από έναν δίσκο προσαύξησης ο οποίος
περιστρέφεται κεπλεριανά γύρω από μελανή οπή μάζας M = 5M⊙ (δηλ. η
ταχύτητα της εκροής είναι αποτέλεσμα της μετατροπής ροής Poynting σε ροή
κινητικής ενέργειας). ϒποθέτοντας ότι ο δίσκος εκτείνεται από ϖin ≈ 3rS ως
ϖout ≈ 5rS, όπου rS = 2GM∕c2 η ακτίνα Schwarzschild, και ότι κοντά στον
δίσκο Bp ≈ |Bϕ|, εκτιμήστε την ένταση του μαγνητικού πεδίου κοντά στον
δίσκο.
Δίνονται c = 3 × 1010cm s-1, G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g
και η ροή Poynting 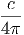 E ×B.
E ×B.
Από δίσκο κοντά σε μελανή οπή μάζας 108M
⊙ ξεκινά μια μαγνητισμένη
εκροή ηλεκτρονίων-πρωτονίων. Η εκροή ξεκινά από μια μικρή περιοχή του
δίσκου 5rg < ϖi < 6rg με V pi = 0.1c, Ti = 1010K, B
pi = 104G, |B
ϕ|i = 103G
και μεταφέρει μάζα με ρυθμό Ṁ = 10-3M
⊙yr-1.
(α) Να υπολογιστούν οι τιμές των ολοκληρωμάτων κίνησης Ω, ΨA, μ, L.
(β) Θεωρήστε ότι κατά μήκος της ροής όλη η ενέργεια και στροφορμή
μεταφέρονται στην ύλη. Ποια η ασυμπτωτική τιμή του παράγοντα Lorentz; Αν
η ασυμπτωτική αζιμουθιακή ταχύτητα της ροής είναι V ϕ∞ = 10-5c ποια η
ασυμπτωτική κυλινδρική ακτίνα της ροής ϖ∞;
Δίδονται G = 6.67 × 10-8 cm3g-1s-2, m
p = 1.67 × 10-24g, k
B = 1.38 × 10-16
erg K-1, c = 3 × 1010 cm s-1, M
⊙ = 2 × 1033g, 1yr= 3 × 107s, και
rg = 2GM∕c2, Ψ
A = (4πγρ0V p ΔS)∕(Bp ΔS), μ = ξγ - ϖΩBϕ∕ΨAc2,
L = ξγϖV ϕ - ϖBϕ∕ΨA.
(α) Δείξτε ότι για μια στάσιμη υδροδυναμική ροή το ολοκλήρωμα της
ενέργειας γράφεται 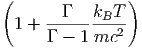 γ = σταθ., όπου m η μέση μάζα ηρεμίας
των σωματίων της ροής.
γ = σταθ., όπου m η μέση μάζα ηρεμίας
των σωματίων της ροής.
(β) Μια υδροδυναμική εκροή αποτελούμενη από πρωτόνια-ηλεκτρόνια έχει
θερμοκρασία Ti = 1012K κοντά στη βάση της. Ποιο το μέγιστο γ που μπορεί
να αποκτήσει; Επαναλάβατε στην περίπτωση που η εκροή αποτελείται από
ηλεκτρόνια-ποζιτρόνια.
Δίνονται οι σταθερές (στο σύστημα cgs ): c = 3 × 1010, k
B = 1.38 × 10-16,
mp = 1.67 × 10-24, m
e = 9.11 × 10-28.
(α) Ποιες οι δυνάμεις που ασκούνται σε μια kra, ιδεατή μαγνητισμένη
εκροή; Γράψτε την εξίσωση ορμής.
(β) Ποιες από τις δυνάμεις μπορούν να επιταχύνουν μια κρύα ροή;
Πολλαπλασιάζοντας την εξίσωση ορμής με V δείξτε ότι ο ρυθμός αύξησης του
παράγοντα Lorentz είναι
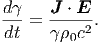
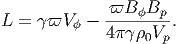
΄Εστω ότι μελετούμε μια υδροδυναμική, σφαιρικά συμμετρική ροή, η οποία
έχει ταχύτητα V = V (r) και παράγοντα Lorentz γ = (1 - V 2∕c2)-1∕2,
πυκνότητα στο σύστημα ηρεμίας της ρ0 = ρ0(r) και πίεση P = P(r). Η ροή
ξεκινά από ακτίνα ri με σχετικιστική θερμοκρασία P(ri) » ρ0(ri)c2 και έχει
πολυτροπικό δείκτη Γ = 4∕3.
και παράγοντα Lorentz γ = (1 - V 2∕c2)-1∕2,
πυκνότητα στο σύστημα ηρεμίας της ρ0 = ρ0(r) και πίεση P = P(r). Η ροή
ξεκινά από ακτίνα ri με σχετικιστική θερμοκρασία P(ri) » ρ0(ri)c2 και έχει
πολυτροπικό δείκτη Γ = 4∕3.
(α) Ολοκληρώστε την εξίσωση συνέχειας ∇⋅ (γρ0V ) = 0 και απλοποιήστε το
αποτέλεσμα αν V ≈ c. Τι εκφράζει η σταθερά της ολοκλήρωσης;
Δίνεται η απόκλιση σε σφαιρικές συντεταγμένες
∇ ⋅A = 1 _
r2 ∂(r2A
r)
∂r + 1 ___
r sin θ ∂(Aθ sin θ)
∂θ + 1 ___
r sin θ ∂Aϕ
∂ϕ .
(β) Η εξίσωση ορμής δίνει το ολοκλήρωμα ξγ = σταθερό, ενώ ο πρώτος νόμος
της θερμοδυναμικής δίνει P∕ρ0Γ = σταθερό. Συνδυάζοντας τις προηγούμενες
σχέσεις με το ολοκλήρωμα που βρήκατε στο προηγούμενο ερώτημα δείξτε ότι
όσο η θερμοκρασία παραμένει σχετικιστική (ξ = 1 + 4P∕ρ0c2 ≈ 4P∕ρ
0c2) ο
παράγοντας Lorentz αυξάνει γραμμικά με την απόσταση r. Επίσης δείξτε ότι η
θερμοκρασία μειώνεται σαν T ∝ r-1, η πυκνότητα σαν ρ
0 ∝ r-3 και η πίεση
σαν P ∝ r-4.
(γ) Μέχρι ποια απόσταση ο παράγοντας Lorentz αυξάνει; Ποια είναι η μέγιστη
τιμή του σαν συνάρτηση των αρχικών ρ0(ri),P(ri),γ(ri);
΄Εστω εκροή η οποία έχει θερμοκρασία T κοντά στην πηγή της (όπου γ ≈
1), με 6 × 109K « T « 1013K ⇔ m
ec2∕k
B « T « mpc2∕k
B. Η εκροή είναι
οπτικά αδιαφανής και αποτελείται από πρωτόνια με αριθμητική πυκνότητα np,
ηλεκτρόνια, φωτόνια και ζεύγη ηλεκτρονίων–ποζιτρονίων, σε θερμοδυναμική
ισορροπία. Δείξτε ότι ο μέγιστος παράγοντας Lorentz που θα αποκτήσει η
εκροή λόγω θερμικής επιτάχυνσης είναι γ = 180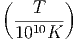 4
4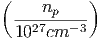 -1.
-1.
Θεωρήστε γνωστό ότι η πίεση των φωτονίων είναι Pγ =  αBBT4 και η
ενεργειακή τους πυκνότητα είναι ργc2 = 3P
γ.
αBBT4 και η
ενεργειακή τους πυκνότητα είναι ργc2 = 3P
γ.
Επίσης, σε θερμοκρασίες T » mec2∕k
B και πυκνότητες πρωτονίων τέτοιες
ώστε 0.04 « 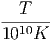
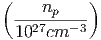 -1∕3 « 0.5 ⇔ n
p « ne± « (mp∕me)np
και
-1∕3 « 0.5 ⇔ n
p « ne± « (mp∕me)np
και 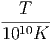 » 0.27
» 0.27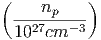 1∕4 ⇔ n
pmpc2 « 11P
γ, που σημαίνει ότι η
πίεση και η ενεργειακή πυκνότητα κυριαρχούνται από τα φωτόνια και τα ζεύγη
ηλεκτρονίων–ποζιτρονίων ενώ η μάζα κυριαρχείται από τα πρωτόνια, η πίεση
των ζευγών ηλεκτρονίων–ποζιτρονίων είναι Pe± = (7∕4)Pγ, η αριθμητική τους
πυκνότητα είναι ne± = 0.833 Pγ∕kBT και η ενεργειακή τους πυκνότητα είναι
ρe±c2 = 3P
e±.
1∕4 ⇔ n
pmpc2 « 11P
γ, που σημαίνει ότι η
πίεση και η ενεργειακή πυκνότητα κυριαρχούνται από τα φωτόνια και τα ζεύγη
ηλεκτρονίων–ποζιτρονίων ενώ η μάζα κυριαρχείται από τα πρωτόνια, η πίεση
των ζευγών ηλεκτρονίων–ποζιτρονίων είναι Pe± = (7∕4)Pγ, η αριθμητική τους
πυκνότητα είναι ne± = 0.833 Pγ∕kBT και η ενεργειακή τους πυκνότητα είναι
ρe±c2 = 3P
e±.
Δίνεται η έκφραση της ενθαλπίας ανά μάζα (προς c2):
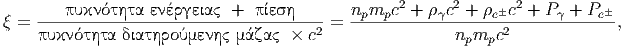
και οι σταθερές αBB = 7.564 × 10-15(cgs), mp = 1.673 × 10-24g, c =
3 × 1010cm s-1.
Γραμμοσκιάστε στο διάγραμμα την περιοχή θερμοκρασιών–πυκνοτήτων όπου
ισχύουν οι υποθέσεις που προαναφέρθηκαν.
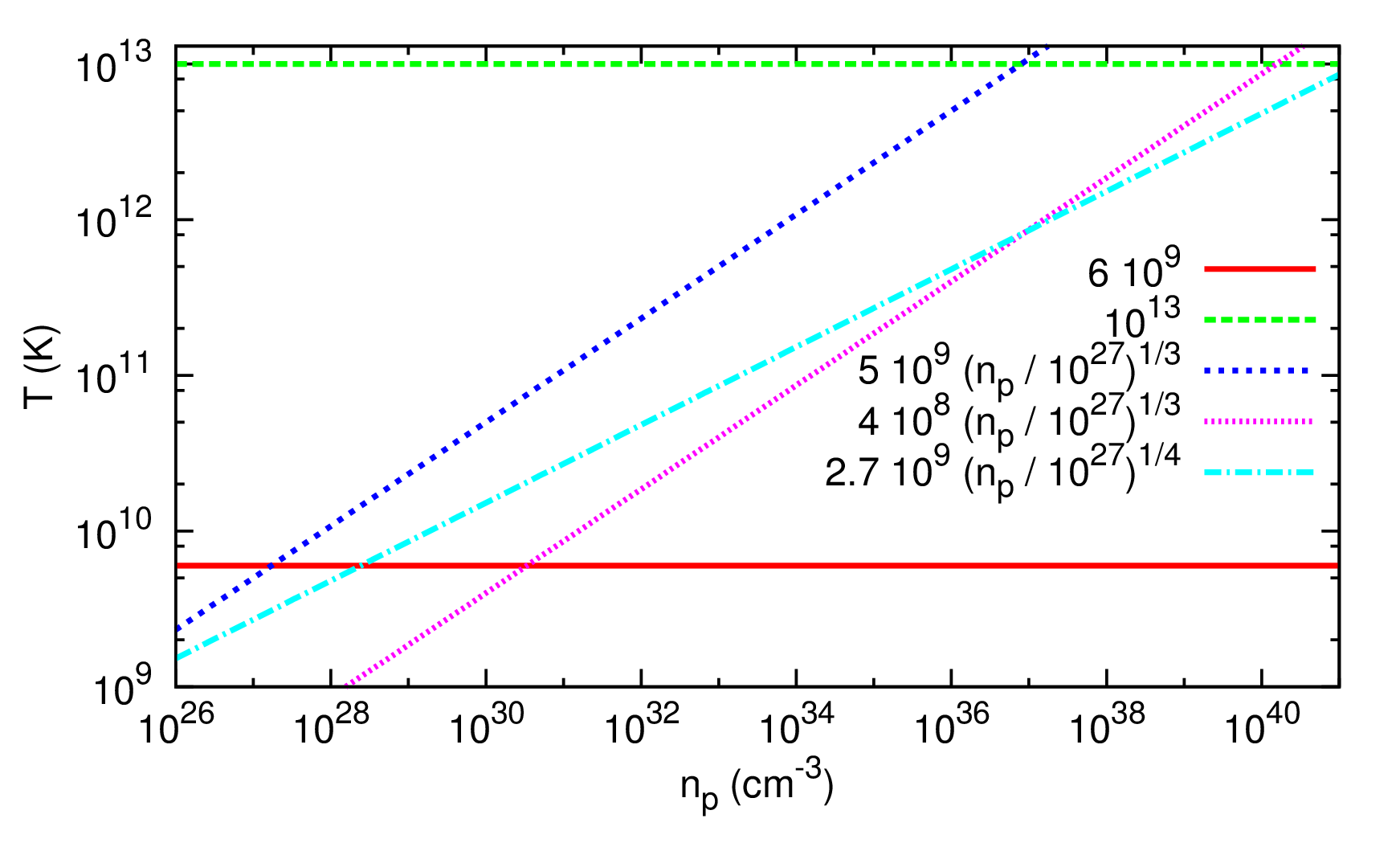
Σχεδιάστε πάνω στο διάγραμμα την καμπύλη που αντιστοιχεί σε σταθερή τιμή του παράγοντα Lorentz, γ = 500. Ποια η ελάχιστη τιμή της T για αυτή την τιμή του γ;
(α) ΄Εστω μαγνητισμένη εκροή από επιφάνεια ΔS δίσκου προσαύξησης που
περιστρέφεται κεπλεριανά με Ω = 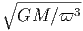 γύρω από κεντρικό σώμα μάζας
M. ϒποθέτοντας για το ηλεκτρικό και μαγνητικό πεδίο ότι E =
γύρω από κεντρικό σώμα μάζας
M. ϒποθέτοντας για το ηλεκτρικό και μαγνητικό πεδίο ότι E = 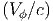 B,
|Bϕ| = B, συμπληρώστε την ακόλουθη έκφραση της ηλεκτρομαγνητικής
ενέργειας που εκλύεται ανά χρόνο:
B,
|Bϕ| = B, συμπληρώστε την ακόλουθη έκφραση της ηλεκτρομαγνητικής
ενέργειας που εκλύεται ανά χρόνο:
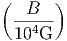 ;
;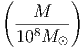 ;
;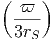 ;
;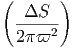 ; ergs s-1.
; ergs s-1. Μια έκλαμψη ακτίνων γ δημιουργείται σε εκροή που ξεκινά από δίσκο προσαύξησης ακτίνας ϖi = 107 cm. Στην περιοχή του δίσκου υπάρχει ηλεκτρομαγνητικό πεδίο Ei ≈ Bi ≈ 1013 G και άρα εκρέει ροή Poynting P i. Ταυτόχρονα, εκρέει πλάσμα πρωτονίων-ηλεκτρονίων με ταχύτητα V i = 0.8c, γi = 5∕3 και πυκνότητα ρ0i = 50 g cm-3.
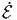 i και ο ρυθμός εκροής μάζας Ṁ.
i και ο ρυθμός εκροής μάζας Ṁ.
Δίνονται c = 3 × 1010, σ T = 0.665 × 10-24, m p = 1.67 × 10-24, όλα στο σύστημα cgs.
Από έναν ενεργό γαλαξιακό πυρήνα ακτινοβολείται ενέργεια ανά χρόνο
L = 1046 erg s-1.
(α) Αν η ενέργεια αυτή, πριν ακτινοβοληθεί, ήταν κινητική ενέργεια εκροής με
παράγοντα Lorentz γ = 10, ποιος ο ρυθμός Ṁ της εκροής σε ηλιακές μάζες ανά
έτος;
(β) ΄Εστω ότι αυτή η κινητική ενέργεια είναι αποτέλεσμα μαγνητικής
επιτάχυνσης σε μια εκροή που προέρχεται από τα εσωτερικά μέρη δίσκου
προσαύξησης ο οποίος περιστρέφεται κεπλεριανά γύρω από μελανή οπή μάζας
M = 108M
⊙ (δηλ. η ταχύτητα της εκροής είναι αποτέλεσμα της μετατροπής
ροής Poynting σε ροή κινητικής ενέργειας). ϒποθέτοντας ότι ο δίσκος έχει
τυπική ακτίνα ϖ0 ≈ 10GM∕c2, επιφάνεια 2πϖ
02, και ότι κοντά στον δίσκο
Bp ≈|Bϕ|, εκτιμήστε την ένταση του μαγνητικού πεδίου κοντά στον δίσκο.
(γ) Συμπληρώστε γενικότερα τη σχέση:
L = …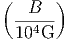

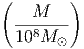

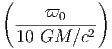
 .
.
Δίνονται c = 3 × 1010cm s-1, G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g
και η ροή Poynting 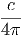 E ×B.
E ×B.
΄Ενας αστέρας νετρονίων με μάζα M = 1.4M⊙ και ακτίνα R = 10 km
περιστρέφεται με περίοδο P = 0.2 s. Μέσω μαγνητισμένου ανέμου χάνει
στροφορμή και ενέργεια με αποτέλεσμα η περίοδός του να αυξάνεται με ρυθμό
Ṗ = 10-15.
(α) Πόση ενέργεια χάνει ανά χρόνο (υπολογίστε το IΩ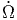 με I =
με I = 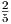 MR2);
MR2);
(β) Με δεδομένο ότι στην απόσταση του κυλίνδρου φωτός RLC = c∕Ω οι τιμές
του πολοειδούς μαγνητικού πεδίου, του αζιμουθιακού μαγνητικού πεδίου και
του ηλεκτρικού πεδίου είναι ίσες μεταξύ τους (E ≈ Bϕ ≈ Bp = BLC) και ότι η
επιφάνεια στην απόσταση αυτή είναι 4πRLC2, δείξτε ότι η ισχύς Poynting είναι
cBLC2R
LC2.
(γ) Αν το πολοειδές μαγνητικό πεδίο είναι διπολικό, οπότε BLC = B⋆(R∕RLC)3
με B⋆ το πεδίο στην επιφάνεια του αστέρα, δείξτε ότι η ενέργεια που απάγει ο
άνεμος ανά μονάδα χρόνου είναι 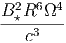 .
.
(δ) ϒπολογίστε το μαγνητικό πεδίο του αστέρα.
Δίνονται M⊙ = 2 × 1033g, c = 3 × 1010cm s-1.
Landau, L. D. & Lifshitz E. M. (1980). Statistical Physics. 3rd edition.
Beskin, V. S. (2010). MHD Flows in Compact Astrophysical Objects. Springer.
Meier, D. L. (2012). Black Hole Astrophysics: The Engine Paradigm. Springer.
Vlahakis, N. (2010). “Output from MHD models”. Lecture Notes in Physics 793,
51.
Vlahakis, N. (2015). “Theory of Relativistic Jets”. Astrophysics and Space Science
Library, 414, 177.
Αστροφυσικοί δίσκοι προσαύξησης έχουν άμεσα ή έμμεσα παρατηρηθεί γύρω από πληθώρα κατηγοριών κεντρικών σωμάτων, άστρων και γαλαξιών. Παραδείγματα αποτελούν η προσρόφηση ύλης από τον συνοδό αστέρα σε ένα διπλό σύστημα, οι δίσκοι γύρω από πρωτοαστέρες που οφείλονται στην κατάρρευση των νεφών που δημιούργησαν τους ίδιους τους πρωτοαστέρες, καθώς και οι δίσκοι στα κέντρα γαλαξιών. Γενικά οι δισκοειδείς σχηματισμοί σε αστροφυσική κλίμακα είναι άμεση συνέπεια της διατήρησης στροφορμής. Η οσοδήποτε μικρή αρχική γωνιακή ταχύτητα της προσπίπτουσας ύλης οδηγεί σε πολύ μεγαλύτερες γωνιακές ταχύτητες σε μικρότερες αποστάσεις και ανάπτυξη ισχυρών φυγόκεντρων δυνάμεων που επιβραδύνουν την πρόσπτωση στο επίπεδο κάθετα στον άξονα περιστροφής. Μιας και στις υπόλοιπες διευθύνσεις η επιβράδυνση λόγω φυγόκεντρου είναι πολύ μικρότερη, ακόμα και αν ξεκινήσουμε με σφαιρικά συμμετρική κατανομή καταλήγουμε σε δισκοειδή.
Μερικοί από τους λόγους για τους οποίους είναι χρήσιμο να μελετήσουμε τους δίσκους ακολουθούν: Η πρόσπτωση ύλης σε συμπαγή αντικείμενα (λευκούς νάνους, αστέρια νετρονίων και μαύρες τρύπες) – η οποία συνοδεύεται από απώλεια μεγάλου ποσού δυναμικής ενέργειας – αποτελεί μηχανισμό έκλυσης ενέργειας με μεγάλη απόδοση (μεγαλύτερη ακόμα και από την απόδοση των θερμοπυρηνικών αντιδράσεων που συμβαίνουν στα κέντρα των άστρων). Είναι γενικά οι τροφοδότες της συντριπτικής πλειοψηφίας των ενεργητικών φαινομένων που παρατηρούμε, συμπεριλαμβανομένων και των εκροών πλάσματος, των οποίων καθορίζουν τις αρχικές συνθήκες. Αποτελούν το περιβάλλον στο οποίο δημιουργούνται οι πλανήτες και η κατανόησή τους είναι απαραίτητη αν θέλουμε να καταλάβουμε τον μηχανισμό δημιουργίας αστρικών συστημάτων όπως το ηλιακό.
Θα τους μελετήσουμε στην απλούστερη εκδοχή τους, θεωρώντας ότι το βαρυτικό πεδίο δημιουργείται από το κεντρικό σώμα και μόνο (αγνοώντας δηλ. την ιδιοβαρύτητά τους), χωρίς μαγνητικά πεδία και χωρίς να λάβουμε υπόψη τη σχετικότητα (ειδική ή γενική).
Αν σκεφτούμε το πρόβλημα της κίνησης ενός μεμονωμένου σωματίου το οποίο κινείται μέσα σε ένα βαρυτικό πεδίο που δημιουργεί μάζα M, συμπεραίνουμε ότι το σωμάτιο εκτελεί τροχιά με σχήμα κωνικής τομής και λόγω διατήρησης στροφορμής αποκλείεται να πέσει πάνω στο κεντρικό σώμα (εξαιρούνται τα σωμάτια των οποίων η αρχική ταχύτητα έχει φορά προς το σώμα M κάτι που όμως έχει πολύ μικρή πιθανότητα να συμβεί). Το ίδιο αποτέλεσμα προκύπτει αν σκεφτούμε τη συλλογική κίνηση υδροδυναμικού πλάσματος στο επίπεδο κάθετα στην αρχική στροφορμή. ϒποθέτοντας στάσιμη κατάσταση (∂∕∂t = 0) και αξισυμμετρία (∂∕∂ϕ = 0) σε ένα ιδανικό ρευστό όπως αυτό που μελετήσαμε στο κεφάλαιο 9, καταλήγουμε στη διατήρηση της στροφορμής ανά μονάδα μάζας L = ϖV ϕ (σημειώστε ότι ξγ ≈ 1 για μη σχετικιστική κίνηση, ενώ έχουμε αγνοήσει τα μαγνητικά πεδία). Ως εκ τούτου, αποκλείεται κάποια ποσότητα ύλης δm να προσπέσει στο κεντρικό αντικείμενο. Αντί αυτού θα είναι υποχρεωμένη να περιστρέφεται επ΄ άπειρον στη γειτονιά μιας κυλινδρικής ακτίνας ϖ, οπότε δεν έχουμε την επιθυμητή μείωση της βαρυτικής δυναμικής ενέργειας μεταξύ δm και M.
Απαιτείται να υπάρχει κάποιος μηχανισμός ο οποίος μέσω κάποιας ροπής δύναμης
θα οδηγεί σε απώλεια στροφορμής, με άλλα λόγια σε ροή στροφορμής προς τα
«έξω», δηλ. σε φορά αντίθετη από την κατεύθυνση προς το κεντρικό αντικείμενο.
Αποτέλεσμα αυτού του μηχανισμού θα είναι η στροφορμή της μάζας δm να
ελαττώνεται και τελικά η μάζα αυτή να προσπίπτει στο κεντρικό σώμα. Ταυτόχρονα,
καθώς η μάζα κινείται από μια αρχική ακτίνα ϖi σε μια τελική ϖf η απώλεια
μηχανικής ενέργειας η οποία από το θεώρημα Virial σχετίζεται με το μισό της
απώλειας δυναμικής ενέργειας 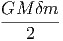
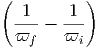 μετασχηματίζεται σε κάποια
άλλη μορφή ενέργειας, π.χ. περιστροφική κινητική ενέργεια, ακτινοβολία, θερμότητα,
ενέργεια μαγνητικού πεδίου, κ.ο.κ.
μετασχηματίζεται σε κάποια
άλλη μορφή ενέργειας, π.χ. περιστροφική κινητική ενέργεια, ακτινοβολία, θερμότητα,
ενέργεια μαγνητικού πεδίου, κ.ο.κ.
Το πρόβλημα της απώλειας στροφορμής στους αστροφυσικούς δίσκους έχει απασχολήσει πολύ την επιστημονική κοινότητα ιδιαίτερα τις τελευταίες δεκαετίες. Οι επικρατέστεροι μηχανισμοί είναι δύο: Ο πρώτος σχετίζεται με μαγνητοϋδροδυναμικές εκροές. ΄Οπως έχουμε ήδη αναλύσει στο κεφάλαιο 9, η εκροή μεταφέρει στροφορμή (και το πεδίο αλλά και η ύλη μεταφέρουν στροφορμή), η οποία πηγάζει από τον δίσκο (ή γενικότερα τη βάση της εκροής). Ειδικότερα στην κατηγορία δίσκων γύρω από πρωτοαστέρες πρόσφατες παρατηρήσεις πιδάκων δείχνουν ότι πράγματι μεταφέρουν στροφορμή ίδιας τάξης μεγέθους με αυτή που χάνει ο δίσκος.
Ο δεύτερος μηχανισμός που θα αναλύσουμε περισσότερο στο παρόν κεφάλαιο βασίζεται στην έννοια του ενεργού ιξώδους.
Γενικά όταν ένα ρευστό κινείται με μη ομογενή ταχύτητα V , γειτονικές περιοχές έχουν διαφορετικές ταχύτητες και αναπτύσσονται δυνάμεις εσωτερικής τριβής οι οποίες μεταφέρουν ορμή από τα γρηγορότερα στα αργότερα μέρη της ροής (μετατρέποντας παράλληλα μέρος της ενέργειας σε θερμότητα). Οι δυνάμεις αυτές περιγράφονται από τους δύο τελευταίους όρους της εξίσωσης ορμής (7.3)
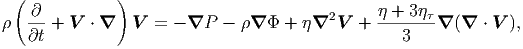 | (10.1) |
όπου ρ είναι η πυκνότητα μάζας, Φ το βαρυτικό δυναμικό και η και ητ οι συντελεστές μοριακού ιξώδους. Οι αντίστοιχοι συντελεστές κινηματικού ιξώδους είναι ν = η∕ρ και ντ = ητ∕ρ. Για ένα αέριο σε τάξη μεγέθους ο συντελεστής ν είναι ίσος με το γινόμενο της μέσης ελεύθερης διαδρομής με τη θερμική ταχύτητα, ενώ ο ντ είναι αμελητέος για μονατομικά αέρια. Για εφαρμογές σε αστροφυσικούς δίσκους η επίδραση του μοριακού ιξώδους είναι αμελητέα, παρόλα αυτά μπορεί να αντικατασταθεί με «ενεργό» ιξώδες το οποίο έχει παρόμοια συμπεριφορά (αλλά πολύ μεγαλύτερο συντελεστή ιξώδους). Σε έναν υδροδυναμικό δίσκο το ενεργό ιξώδες μπορεί να οφείλεται σε τύρβη, με τις δίνες να αντικαθιστούν τα μόρια. Σε μια τυρβώδη ροή μπορούμε να αναλύσουμε όλα τα μεγέθη (ρ, V , P) σε μία μέση τιμή (ρ, V , P) συν μια διακύμανση (ρ′, V ′, P′) η οποία έχει μηδενική χρονική μέση τιμή (< ρ′ >= 0, < V ′ >= 0, < P′ >= 0). Αντικαθιστώντας στην εξίσωση της ορμής έχουμε μετά από πράξεις (και αφού πάρουμε τη μέση τιμή της ίδιας της εξίσωσης ορμής)
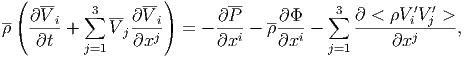 | (10.2) |
όπου i = 1, 2, 3 και x1 = x, x2 = y, x3 = z. Ο τελευταίος όρος της παραπάνω εξίσωσης παριστάνει το ενεργό ιξώδες λόγω τυρβώδους ροής, το οποίο μπορεί να ιδωθεί ως μια επιπλέον δύναμη η οποία επηρεάζει τη μέση ροή (επίσης ο όρος αυτός μεταφέρει ενέργεια από σχηματισμούς μεγαλύτερης σε σχηματισμούς μικρότερης κλίμακας μέσα στην τυρβώδη ροή, με τελικό αποτέλεσμα ενεργειακές απώλειες). Το να περιγράψουμε αυτόν τον όρο είναι ένα δύσκολο πρόβλημα το οποίο μπορεί να μελετηθεί μόνο υπολογιστικά. Αναλυτικές μέθοδοι βασίζονται σε φαινομενολογικές εκτιμήσεις του όρου αυτού, όπως θα δούμε στα επόμενα.
Εναλλακτικά, το ενεργό ιξώδες μπορεί να οφείλεται σε δίνες μαγνητικού πεδίου. Οι Balbus & Hawley, χρησιμοποιώντας μια μελέτη του Chandrasekhar, έχουν δείξει ότι σε έναν δίσκο με σχετικά ασθενές μαγνητικό πεδίο, ο οποίος περιστρέφεται διαφορικά, αναπτύσσεται μια αστάθεια που ονομάστηκε μαγνητοπεριστροφική. Η αστάθεια αυτή οδηγεί στην ενίσχυση του μαγνητικού πεδίου και τη δημιουργία τυρβώδους κατάστασης, όμοιας με την υδροδυναμική περίπτωση. Η διαφορά είναι ότι ο σημαντικός επιπλέον όρος στην εξίσωση ορμής είναι ανάλογος του < Bϖ′Bϕ′ >. Αυτός ο μηχανισμός θεωρείται ο επικρατέστερος (μαζί με την απώλεια στροφορμής λόγω εκροής), παρότι αρκετές λεπτομέρειες μένουν ακόμα προς διερεύνηση.
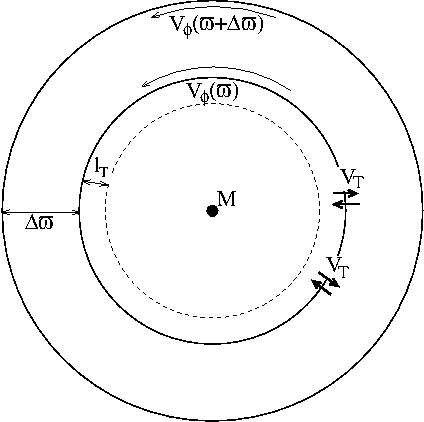
Ακολουθεί μια απλούστερη μελέτη της επίδρασης του ενεργού ιξώδους σε
έναν αστροφυσικό δίσκο είτε αυτό οφείλεται σε τυρβώδη υδροδυναμική ροή
είτε στη μαγνητοπεριστροφική αστάθεια. ΄Εστω ότι μελετούμε την κίνηση
δαχτυλιδιού πάχους Δϖ, με εσωτερική ακτίνα ϖ και εξωτερική ϖ + Δϖ,
σε έναν δίσκο γύρω από μια σημειακή μάζα M, όπως στο σχήμα 10.1. Η
κεπλεριανή ταχύτητα είναι V ϕ = 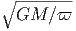 , ενώ η στροφορμή ανά μονάδα
μάζας είναι ϖV ϕ =
, ενώ η στροφορμή ανά μονάδα
μάζας είναι ϖV ϕ = 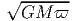 . Από αυτές τις σχέσεις βλέπουμε ότι όσο το ϖ
ελαττώνεται η περιστροφική ταχύτητα αυξάνεται ενώ η στροφορμή ελαττώνεται.
Συνεπώς για να κινηθεί ένα δαχτυλίδι προς τα μέσα πρέπει να ελαττωθεί η
στροφορμή του. Στο απλό μοντέλο που φαίνεται στο σχήμα 10.1 και όπου δεν
λαμβάνονται υπόψη οι ακτινικές κινήσεις της μέσης ροής, η ολική μάζα που
ανταλλάσσεται μεταξύ του δαχτυλιδιού Δϖ και του αμέσως εσωτερικού του είναι
κατά μέσο όρο μηδέν. Παρ΄ όλα αυτά, κοιτάζοντας τη μικροκλίμακα και τους
σχηματισμούς της τυρβώδους ροής που χαρακτηρίζονται από ταχύτητες
V T και μέγεθος lT , υλικό από ακτίνες ϖ - lT μικρότερες της μικρότερης
ακτίνας του δαχτυλιδιού μπορεί να περάσει στο δαχτυλίδι και θα καταλήξει να
περιστρέφεται με μικρότερη γωνιακή ταχύτητα. Η αρχική γωνιακή ταχύτητα
αυτού του υλικού είναι Ω(ϖ - lT ) ≈ Ω(ϖ) -
. Από αυτές τις σχέσεις βλέπουμε ότι όσο το ϖ
ελαττώνεται η περιστροφική ταχύτητα αυξάνεται ενώ η στροφορμή ελαττώνεται.
Συνεπώς για να κινηθεί ένα δαχτυλίδι προς τα μέσα πρέπει να ελαττωθεί η
στροφορμή του. Στο απλό μοντέλο που φαίνεται στο σχήμα 10.1 και όπου δεν
λαμβάνονται υπόψη οι ακτινικές κινήσεις της μέσης ροής, η ολική μάζα που
ανταλλάσσεται μεταξύ του δαχτυλιδιού Δϖ και του αμέσως εσωτερικού του είναι
κατά μέσο όρο μηδέν. Παρ΄ όλα αυτά, κοιτάζοντας τη μικροκλίμακα και τους
σχηματισμούς της τυρβώδους ροής που χαρακτηρίζονται από ταχύτητες
V T και μέγεθος lT , υλικό από ακτίνες ϖ - lT μικρότερες της μικρότερης
ακτίνας του δαχτυλιδιού μπορεί να περάσει στο δαχτυλίδι και θα καταλήξει να
περιστρέφεται με μικρότερη γωνιακή ταχύτητα. Η αρχική γωνιακή ταχύτητα
αυτού του υλικού είναι Ω(ϖ - lT ) ≈ Ω(ϖ) -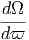 lT και αφού
lT και αφού 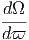 < 0 είναι
μεγαλύτερη της τελικής Ω(ϖ). Αν η επιφανειακή πυκνότητα του δίσκου
είναι
< 0 είναι
μεγαλύτερη της τελικής Ω(ϖ). Αν η επιφανειακή πυκνότητα του δίσκου
είναι
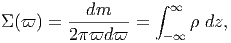
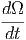 =
= 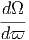
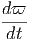 , όπου
, όπου 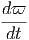 = V T είναι η χαρακτηριστική ταχύτητα της τύρβης. Είναι
δηλ.
= V T είναι η χαρακτηριστική ταχύτητα της τύρβης. Είναι
δηλ.
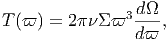 | (10.3) |
όπου ν = lT V T είναι ο συντελεστής κινηματικού ιξώδους λόγω τυρβώδους ροής (ο οποίος κατά κανόνα είναι πολλές τάξεις μεγέθους μεγαλύτερος από τον αντίστοιχο συντελεστή μοριακού ιξώδους).
΄Ομοια, υλικό έξω από το δαχτυλίδι, από ακτίνες ϖ + Δϖ + lT μπορεί να περάσει
προς τα μέσα και καθώς αρχικά περιστρέφεται πιο αργά, θα επιταχυνθεί από το
δαχτυλίδι. ΄Οπως και πριν μπορούμε να υπολογίσουμε τη ροπή δύναμης που του ασκεί
το δαχτυλίδι, η οποία προκύπτει -![[ ]
3dΩ--
2πνΣ ϖ dϖ](HEA_files/HEA436x.png) ϖ+Δϖ = -T(ϖ + Δϖ).
Η συνολική ροπή που ασκεί το δαχτυλίδι στο περιβάλλον του είναι
T(ϖ) -T(ϖ + Δϖ) = -
ϖ+Δϖ = -T(ϖ + Δϖ).
Η συνολική ροπή που ασκεί το δαχτυλίδι στο περιβάλλον του είναι
T(ϖ) -T(ϖ + Δϖ) = -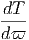 Δϖ, επομένως η ροπή που ασκείται στο δαχτυλίδι από
το περιβάλλον του είναι
Δϖ, επομένως η ροπή που ασκείται στο δαχτυλίδι από
το περιβάλλον του είναι 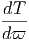 Δϖ. Η ροπή αυτή είναι γενικά ικανή να επιλύσει το
πρόβλημα της απώλειας στροφορμής και να επιτρέψει την ακτινική κίνηση της ύλης
μέσα στο δίσκο προς το κεντρικό σώμα.
Δϖ. Η ροπή αυτή είναι γενικά ικανή να επιλύσει το
πρόβλημα της απώλειας στροφορμής και να επιτρέψει την ακτινική κίνηση της ύλης
μέσα στο δίσκο προς το κεντρικό σώμα.
΄Ενας δίσκος χαρακτηρίζεται λεπτός αν το πάχος του 2H σε απόσταση ϖ από το κεντρικό σώμα είναι πολύ μικρότερο του ϖ, βλέπε σχήμα 10.2. ΄Οπως αναφέρθηκε και στην εισαγωγή, θα αμελήσουμε την ιδιοβαρύτητα του δίσκου (δηλ. θεωρούμε ότι η μάζα του είναι πολύ μικρότερη από την κεντρική μάζα M) και την επίδραση από μαγνητικά πεδία, όχι γιατί είναι ασήμαντη, αλλά για να απλουστεύσουμε κατά το δυνατό τη συζήτηση. Επίσης θα αγνοήσουμε τυχόν εκροή από την επιφάνεια του δίσκου. Τέλος, θα θεωρήσουμε ότι η θερμοκρασία είναι συνάρτηση μόνο της κυλινδρικής απόστασης ϖ και δεν εξαρτάται από τη συντεταγμένη z.
Η απλούστερη προσέγγιση για να καθορίσουμε τη δομή του δίσκου, δηλ. τη σχέση μεταξύ H και ϖ, είναι να υποθέσουμε υδροστατική ισορροπία στην ẑ κατεύθυνση
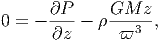
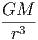 r ⋅ẑ ≈ -ρ
r ⋅ẑ ≈ -ρ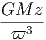 είναι η προβολή της δύναμης βαρύτητας ανά
όγκο στην ẑ κατεύθυνση. Κρατώντας σταθερή την κυλινδρική ακτίνα ϖ η
θερμοκρασία είναι σταθερή, επομένως ισχύει dP = Cs2dρ με C
s =
είναι η προβολή της δύναμης βαρύτητας ανά
όγκο στην ẑ κατεύθυνση. Κρατώντας σταθερή την κυλινδρική ακτίνα ϖ η
θερμοκρασία είναι σταθερή, επομένως ισχύει dP = Cs2dρ με C
s = 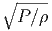 την
ισόθερμη ταχύτητα του ήχου. ΄Ετσι βρίσκουμε τη διαφορική εξίσωση που
ικανοποιεί η πυκνότητα dρ∕ρ = -(GM∕Cs2ϖ3)zdz, της οποίας η λύση
είναι1
την
ισόθερμη ταχύτητα του ήχου. ΄Ετσι βρίσκουμε τη διαφορική εξίσωση που
ικανοποιεί η πυκνότητα dρ∕ρ = -(GM∕Cs2ϖ3)zdz, της οποίας η λύση
είναι1
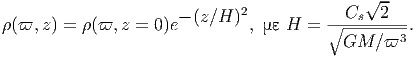
Η εξίσωση ορμής στην  κατεύθυνση είναι
κατεύθυνση είναι
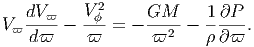
 κατεύθυνση είναι η δύναμη βαρύτητας,
δηλ. αμελώντας την κλίση της πίεσης στην
κατεύθυνση είναι η δύναμη βαρύτητας,
δηλ. αμελώντας την κλίση της πίεσης στην  κατεύθυνση αλλά και τη δύναμη
αδράνειας που σχετίζεται με την ταχύτητα V ϖ, προκύπτει ότι το ρευστό
περιστρέφεται κεπλεριανά, V ϕ ≈ ϖΩ =
κατεύθυνση αλλά και τη δύναμη
αδράνειας που σχετίζεται με την ταχύτητα V ϖ, προκύπτει ότι το ρευστό
περιστρέφεται κεπλεριανά, V ϕ ≈ ϖΩ = 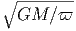 . Αντικαθιστώντας στην
H = Cs
. Αντικαθιστώντας στην
H = Cs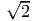 ∕
∕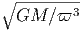 , βρίσκουμε ότι
, βρίσκουμε ότι
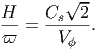 | (10.4) |
Αυτός ο λόγος πρέπει να είναι « 1, για να είναι αυτοσυνεπής ο υπολογισμός και ο
δίσκος να είναι πράγματι λεπτός. Η ανισότητα Cs « V ϕ δικαιολογεί και το ότι
μπορούμε να αγνοήσουμε την κλίση της πίεσης στην ακτινική (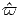 ) συνιστώσα της
εξίσωσης ορμής, αφού η αντίστοιχη επιτάχυνση
) συνιστώσα της
εξίσωσης ορμής, αφού η αντίστοιχη επιτάχυνση 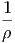
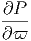 είναι σε τάξη μεγέθους
Cs2∕ϖ, πολύ μικρότερη από τη φυγόκεντρο και τη βαρυτική. Για να είναι
λοιπόν ο δίσκος λεπτός και να περιστρέφεται κεπλεριανά πρέπει να ισχύει
Cs « V ϕ.
είναι σε τάξη μεγέθους
Cs2∕ϖ, πολύ μικρότερη από τη φυγόκεντρο και τη βαρυτική. Για να είναι
λοιπόν ο δίσκος λεπτός και να περιστρέφεται κεπλεριανά πρέπει να ισχύει
Cs « V ϕ.
Λόγω της ακτινικής ταχύτητας V ϖ (< 0), μάζα κινείται προς το κεντρικό σώμα. Από κύκλο ακτίνας ϖ, σε χρόνο Δt περνάει μάζα 2πϖ|V ϖ| dt Σ, όπου Σ είναι η επιφανειακή πυκνότητα (Σ ≈ 2Hρ). ΄Αρα
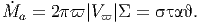 | (10.5) |
είναι ο ρυθμός προσρόφησης της ύλης, ο οποίος για στάσιμη κατάσταση και χωρίς εκροή μάζας από την επιφάνεια του δίσκου είναι ίδιος σε όλες τις ακτίνες ϖ. (Η Ṁa δεν πρέπει να συγχέεται με τον ρυθμό εκρεόμενης μάζας Ṁ που εξετάσαμε στο κεφάλαιο 9. Πρακτικά, το πολύ ένα μικρό μέρος της ύλης που κινείται προς το κέντρο καταφέρνει να διαφύγει δημιουργώντας εκροή, δηλ. Ṁ «Ṁa.)
΄Ενα δαχτυλίδι από ϖ ως ϖ + Δϖ περικλείει μάζα ΔM = Σ2πϖΔϖ. Καθώς η μάζα
αυτή κινείται προς το κέντρο με ακτινική ταχύτητα V ϖ ο ρυθμός μεταβολής της
στροφορμής της είναι ΔM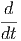 (ϖV ϕ) = ΔM V ϖ
(ϖV ϕ) = ΔM V ϖ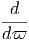 (ϖV ϕ) = -
(ϖV ϕ) = -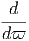 (ṀaϖV ϕ) Δϖ,
αντικαθιστώντας ΔM = Σ2πϖΔϖ και χρησιμοποιώντας την εξίσωση (10.5) με
|V ϖ| = -V ϖ αφού V ϖ < 0.
(ṀaϖV ϕ) Δϖ,
αντικαθιστώντας ΔM = Σ2πϖΔϖ και χρησιμοποιώντας την εξίσωση (10.5) με
|V ϖ| = -V ϖ αφού V ϖ < 0.
Η ροπή που ασκείται στο δαχτυλίδι έχουμε βρει στο τέλος του κεφαλαίου 10.2
ότι είναι 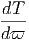 Δϖ. Εξισώνοντας με τον ρυθμό μεταβολής της στροφορμής
βρίσκουμε
Δϖ. Εξισώνοντας με τον ρυθμό μεταβολής της στροφορμής
βρίσκουμε
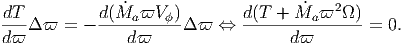
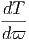 =
= 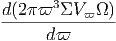 και είναι ισοδύναμη με την
και είναι ισοδύναμη με την 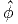 συνιστώσα της εξίσωσης ορμής.) Η παραπάνω εξίσωση ολοκληρώνεται κατευθείαν
και δίνει
συνιστώσα της εξίσωσης ορμής.) Η παραπάνω εξίσωση ολοκληρώνεται κατευθείαν
και δίνει
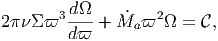
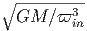 , η σταθερά
της ολοκλήρωσης βρίσκεται C = Ṁa(ϖ2Ω)
in = Ṁa
, η σταθερά
της ολοκλήρωσης βρίσκεται C = Ṁa(ϖ2Ω)
in = Ṁa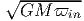 . Τελικά, αφού
χρησιμοποιήσουμε τον κεπλεριανό νόμο Ω =
. Τελικά, αφού
χρησιμοποιήσουμε τον κεπλεριανό νόμο Ω = 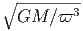 , βρίσκουμε την
ακόλουθη σχέση μεταξύ του ρυθμού προσρόφησης και του συντελεστή
ιξώδους:
, βρίσκουμε την
ακόλουθη σχέση μεταξύ του ρυθμού προσρόφησης και του συντελεστή
ιξώδους:
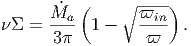 | (10.6) |
Η σχέση αυτή ουσιαστικά μας δίνει ποιο πρέπει να είναι το ιξώδες αν θέλουμε να έχουμε δίσκο με ρυθμό προσρόφησης Ṁa (στον οποίο αντιστοιχεί απώλεια στροφορμής με συγκεκριμένο ρυθμό, που εξασφαλίζεται με το συγκεκριμένο ιξώδες).
Το ιξώδες σαν τριβή που είναι οδηγεί όχι μόνο σε απώλειες στροφορμής, αλλά και σε ενεργειακές απώλειες. Η ροή της ενέργειας που χάνεται είναι ανάλογη της ροπής T, αφού το έργο της δύναμης ιξώδους είναι σε μια περιστροφή TΔϕ = 2πT. ΄Αρα η ενέργεια που χάνεται ανά μονάδα χρόνου και ανά επιφάνεια του δίσκου είναι (λαμβάνοντας υπόψη και τις δύο επιφάνειες του δίσκου)
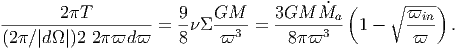
Η προηγούμενη εξίσωση συνεπάγεται ότι καθώς η ύλη εισρέει, από κάθε δαχτυλίδι του δίσκου με επιφάνεια 2 × 2πϖΔϖ (λαμβάνοντας υπόψη και τις δυο επιφάνειες του δίσκου) χάνεται ισχύς
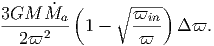
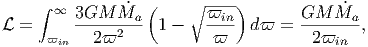
Αν η απόσταση ϖin είναι συγκρίσιμη με τη βαρυτική ακτίνα rg = GM∕c2 (η ακτίνα Schwarzschild είναι 2rg), τότε η απόδοση σε μετασχηματισμό της εισρέουσας ύλης σε ενέργεια είναι L∕Ṁac2 = r g∕2ϖin (δεν έχουμε βέβαια καμία μετατροπή ύλης σε ενέργεια, απλά εκφράζουμε την ισχύ σε μονάδες Ṁac2). Η απόδοση αυτή μπορεί να γίνει πολύ μεγάλη για συμπαγή αντικείμενα· γίνεται μέγιστη αν το κεντρικό σώμα είναι μέγιστα περιστρεφόμενη μελανή οπή τύπου Kerr στην οποία ο δίσκος εκτείνεται μέχρι την ακτίνα τελευταίας ευσταθούς κυκλικής τροχιάς ϖin = rg, ενώ για μη περιστρεφόμενη μελανή οπή τύπου Schwarzschild η ακτίνα τελευταίας ευσταθούς κυκλικής τροχιάς είναι ϖin = 6rg. Κατά κανόνα ξεπερνάει κατά πολύ την απόδοση της πυρηνικής καύσης του υδρογόνου σε ήλιο (η οποία είναι 0.007).
Η πιο απλή υπόθεση για το τι γίνεται αυτή η ισχύς είναι να υποθέσουμε ότι ακτινοβολείται (η απλοϊκή αυτή υπόθεση δεν ισχύει πάντα· σε πολλές περιπτώσεις η ισχύς μπορεί να οδηγήσει σε δημιουργία στέμματος ή στην ενίσχυση μαγνητικών πεδίων). Αν το αέριο του δίσκου είναι οπτικά αδιαφανές τότε ο δίσκος εκπέμπει από την επιφάνειά του ακτινοβολία μέλανος σώματος, με ενεργό θερμοκρασία η οποία μπορεί να βρεθεί από τον νόμο Stefan - Boltzmann:
![[3GM M˙a ( ∘-ϖin) ]1∕4
Teff = --------- 1 - ---- ϖ -3∕4.
8π σSB ϖ](HEA_files/HEA473x.png)
Η θερμοκρασία σε έναν λεπτό αστροφυσικό δίσκο εξαρτάται από την απόσταση από τον άξονα περιστροφής. Για κάθε δαχτυλίδι του δίσκου το οποίο εκπέμπει σαν μέλαν σώμα θερμοκρασίας T(ϖ) η φασματική ένταση ακτινοβολίας είναι ίση με τη συνάρτηση Planck
![[ ]
2hν23 3GM Ma˙ ( ∘ -ϖin) 1∕4 -3∕4
Iν = ----[--chν--]----, T(ϖ ) = --------- 1 - ---- ϖ ,
exp kBT(ϖ) - 1 8π σSB ϖ](HEA_files/HEA474x.png)
![[- --hν--]
kBT(ϖ)](HEA_files/HEA475x.png) . (Σημειώστε ότι ν εδώ είναι η συχνότητα και όχι ο
συντελεστής ιξώδους για τον οποίο χρησιμοποιήσαμε το ίδιο σύμβολο στα
προηγούμενα.)
. (Σημειώστε ότι ν εδώ είναι η συχνότητα και όχι ο
συντελεστής ιξώδους για τον οποίο χρησιμοποιήσαμε το ίδιο σύμβολο στα
προηγούμενα.)
Επομένως, για έναν παρατηρητή σε απόσταση d από τον δίσκο και με γωνία παρατήρησης i (γωνία μεταξύ της ευθείας παρατήρησης και του άξονα περιστροφής του δίσκου) η ροή ακτινοβολίας είναι
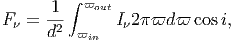
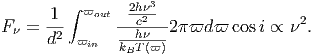
![∫ ϖout 3 [ ] [ ]
Fν = -1- 2h-ν-exp - ---hν--- 2πϖd ϖ cosi ∝ exp - ---hν----- ,
d2 ϖin c2 kBT (ϖ ) kBT (ϖin)](HEA_files/HEA478x.png)
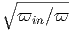 ≈
1 κάτι που ισχύει σε όλο τον δίσκο εκτός από αποστάσεις πολύ κοντά
στην ϖin και να απλοποιήσουμε το ολοκλήρωμα θέτοντας ϖin = 0 και
ϖout = ∞, οπότε
≈
1 κάτι που ισχύει σε όλο τον δίσκο εκτός από αποστάσεις πολύ κοντά
στην ϖin και να απλοποιήσουμε το ολοκλήρωμα θέτοντας ϖin = 0 και
ϖout = ∞, οπότε
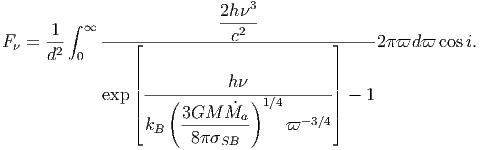
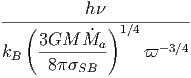 προκύπτει
προκύπτει
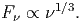
΄Αρα, για το εκπεμπόμενο φάσμα Fν μπορούμε να πούμε ότι αποτελείται από τρία μέρη: (1) Απότομο νόμο δύναμης ν2 σε μικρές συχνότητες από τη μικρότερη θερμοκρασία στο εξωτερικό μέρος του δίσκου ϖout. (2) Νόμο δύναμης ν1∕3 σε ενδιάμεσες συχνότητες από το άθροισμα ακτινοβολίας μέλανος σώματος από πολλές θερμοκρασίες (κάθε δαχτυλίδι έχει διαφορετική θερμοκρασία). (3) Εκθετική πτώση e-hν∕kBTmax σε υψηλές συχνότητες λόγω της μέγιστης θερμοκρασίας κοντά στο ϖin.
Παρότι καταφέραμε να εξάγουμε κάποια συμπεράσματα απλά υποθέτοντας στάσιμη κατάσταση, η ακριβής δομή του δίσκου εξαρτάται από το ενεργό ιξώδες και πώς αυτό μεταβάλλεται μέσα στον δίσκο. Η πρώτη προσπάθεια να λυθεί αυτό το πρόβλημα έγινε από τους Shakura & Sunyaev, οι οποίοι κατάφεραν να λύσουν το πρόβλημα της δομής του δίσκου υποθέτοντας ότι το ιξώδες είναι ανάλογο του γινομένου CsH. Η σταθερά αναλογίας ονομάστηκε α παράμετρος, και οι δίσκοι στους οποίους ν = αCsH ονομάστηκαν α δίσκοι.
Η εξίσωση ενέργειας για το ρευστό που εισρέει (ο πρώτος νόμος θερμοδυναμικής) γράφεται
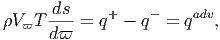
΄Οπως είπαμε και στο κεφάλαιο 10.2, τα μαγνητικά πεδία παίζουν σπουδαίο ρόλο και στους αστροφυσικούς δίσκους. ΄Ηδη μιλήσαμε για τη μαγνητοπεριστροφική αστάθεια η οποία αποτελεί ουσιαστικά έναν τρόπο για να δημιουργηθεί ένα ενεργό (ή ανώμαλο όπως συνηθίζεται να λέγεται) ιξώδες.
Μια άλλη προσπάθεια αποτελεί η περίπτωση όπου ισχυρά μαγνητικά πεδία μεγάλης κλίμακας διαπερνούν τον δίσκο. Σ΄ αυτή την περίπτωση χρειάζεται κάποιος μηχανισμός διάχυσης ώστε η ύλη να περνάει «μέσα» από το μαγνητικό πεδίο, δηλ. να τέμνει τις δυναμικές γραμμές. Μηχανισμοί διάχυσης αποτελούν η Ωμική διάχυση,2 ή η αμφιπολική διάχυση.3
Δείξτε ότι η θερμοκρασία ενός λεπτού δίσκου είναι μέγιστη σε απόσταση (49∕36) × ϖin, όπου ϖin είναι η απόσταση όπου δίσκος και κεντρικό σώμα περιστρέφονται με ίδια γωνιακή ταχύτητα. ϒπολογίστε τη μέγιστη αυτή θερμοκρασία για πρόσπτωση σε μια γρήγορα περιστρεφόμενη μελανή οπή με μάζα M8108M ⊙. Δίνεται Ṁa = Ṁ1M⊙yr-1.
Αν η θερμοκρασία ενός λεπτού και οπτικά αδιαφανούς δίσκου είναι ίση με την ενεργό θερμοκρασία, ποιο είναι το σχήμα του (δηλ. η συνάρτηση H(ϖ) που καθορίζει την επιφάνειά του);
Η παράμετρος α των Shakura & Sunyaev, δεν μπορεί να είναι μεγαλύτερη της μονάδας. Εξηγήστε γιατί.
(α) ϒπολογίστε την ενεργό θερμοκρασία ενός λεπτού δίσκου προσαύξησης. Συγκεκριμένα βρείτε τα T0, n1, n2 και n3 στη σχέση
![[ ] [ ] [ ]
M˙ n1 M n2 ϖ n3 4 πGM mp 2GM
T ≈ T0 -˙-- --8---- -- , όπ ου M˙E = ----------,rg = ---2--.
ME 10 M ⊙ rg 10 σTc c](HEA_files/HEA485x.png)
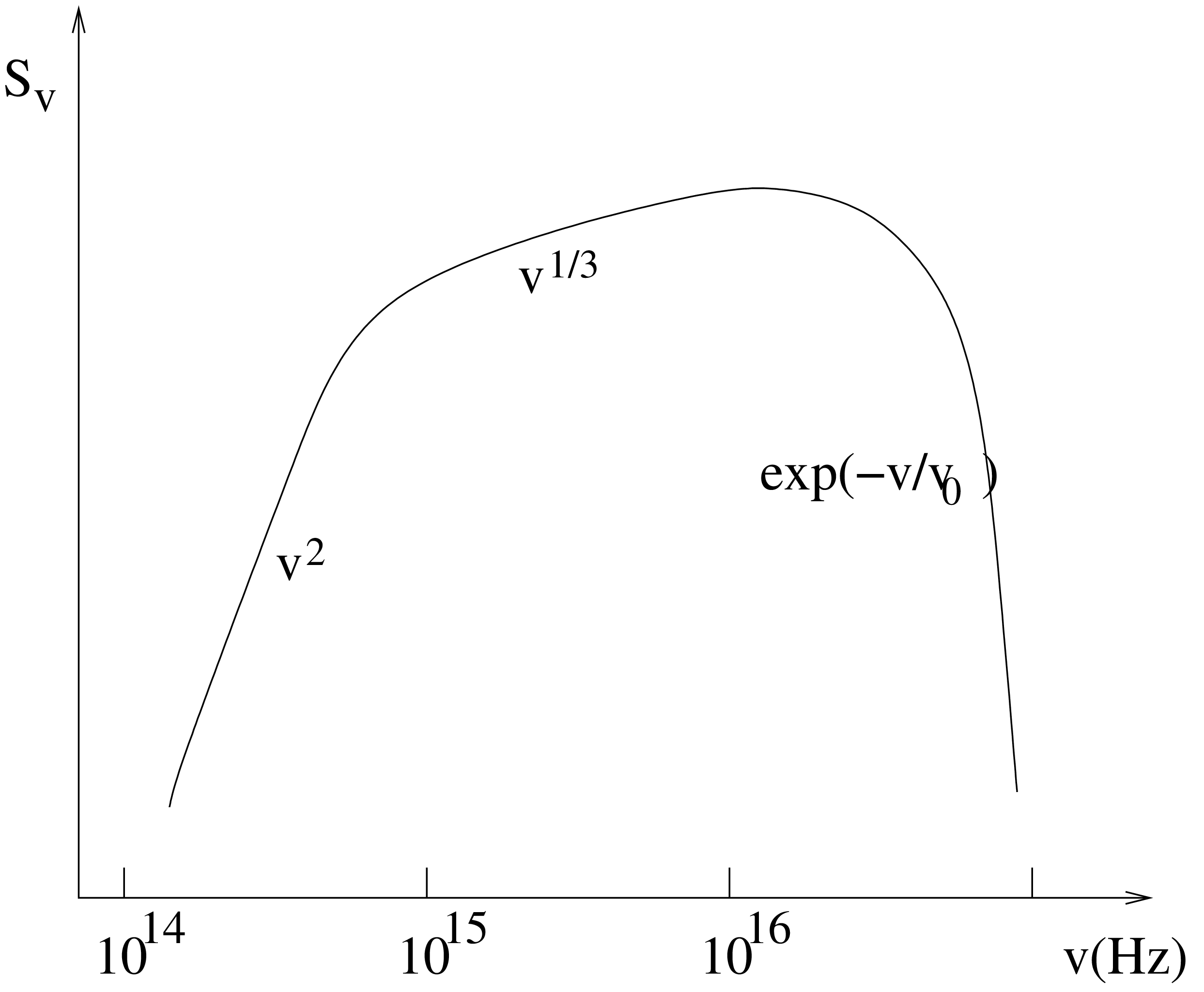
(α) Περιγράψτε το πρόβλημα απώλειας στροφορμής στους αστροφυσικούς
δίσκους. Πόση είναι η στροφορμή που πρέπει να χαθεί ανά μονάδα μάζας και
ποιος είναι ο ρυθμός απώλειας στροφορμής (στροφορμή ανά μονάδα χρόνου)
για έναν δίσκο με ρυθμό προσρόφησης Ṁa;
(β) Ποια η ροή στροφορμής ανά ροή μάζας που μεταφέρει μια μαγνητισμένη
εκροή; Ποιος ο αντίστοιχος ρυθμός μεταβολής (στροφορμή ανά μονάδα
χρόνου); Δείξτε ότι αν η ροή ενέργειας κοντά στη βάση της εκροής κυριαρχείται
από τη ροή Poynting τότε και η στροφορμή κυριαρχείται από το μέρος που
αντιστοιχεί στο ηλεκτρομαγνητικό πεδίο.
(γ) Σ΄ έναν δίσκο που περιστρέφεται κεπλεριανά γύρω από μελανή οπή μάζας
M = 108M
⊙ και έχει εσωτερική/εξωτερική ακτίνα 6 και 8 GM∕c2 αντίστοιχα, ο
ρυθμός προσρόφησης είναι Ṁa = 0.1M⊙yr-1. Ποια είναι η ισχύς της μηχανικής
ενέργειας που απελευθερώνεται καθώς η ύλη εισρέει προς το κέντρο;
Από τον δίσκο αυτό εκρέει ύλη με ρυθμό Ṁw « Ṁa, και στη βάση της
εκροής Bp = 104G. Αν υποθέσουμε ότι όλη η μηχανική ενέργεια που
απελευθερώνεται λόγω της προσρόφησης μετατρέπεται σε ροή Poynting, να
βρεθεί το αζιμουθιακό μαγνητικό πεδίο Bϕ. Δείξτε ότι σε αυτήν την περίπτωση,
η στροφορμή που χάνεται από τον δίσκο είναι ίδιας τάξης μεγέθους με τη
στροφορμή που αποκτά η εκροή.
(Δίνονται G = 6.67 × 10-8 cm3g-1s-2, M
⊙ = 2 × 1033g, 1yr = 3 × 107s, c =
3×1010cm s-1 και οι τύποι ξγϖV
ϕ-ϖBϕ∕ΨA = L, ξγ-ϖΩBϕ∕(ΨAc2) = μ,
ΨA = (2γρV pδS)∕(BpδS∕2π).)
(α) Ποιοι είναι οι πιθανοί μηχανισμοί απώλειας στροφορμής στους
αστροφυσικούς δίσκους;
(β) ΄Εστω ένας αστροφυσικός δίσκος που περιστρέφεται κεπλεριανά στον οποίο
υπάρχει τυρβώδης ροή που χαρακτηρίζεται από μήκος lT και ταχύτητα V T .
Δείξτε ότι η ροπή που ασκείται σε μάζα 2πϖlT Σ (όπου Σ η επιφανειακή
πυκνότητα του δίσκου) είναι T = -3πlT V T Σ .
.
(α) Σε μια κατηγορία αστροφυσικών δίσκων προσαύξησης ισχύει H∕ϖ ≈
Cs∕V ϕ. Αποδείξτε αυτή τη σχέση αναφέροντας όλες τις υποθέσεις που οδηγούν
σε αυτή.
(β) Σε απειροστά λεπτούς δίσκους μπορούμε να θεωρήσουμε ότι η πυκνότητα
έχει τη μορφή ρ = Σ(ϖ)δ(z). Ποια η φυσική σημασία του Σ(ϖ); Δείξτε
ότι η διατήρηση της μάζας οδηγεί σε ένα ολοκλήρωμα που συνδέει αυτήν την
ποσότητα με τη συνιστώσα V ϖ της ταχύτητας.
(α) ϒπολογίστε την ενεργό θερμοκρασία ενός λεπτού δίσκου προσαύξησης
σαν συνάρτηση της απόστασης ϖ, της εσωτερικής ακτίνας του δίσκου ϖin
και της ολικής ισχύος που εκπέμπει ο δίσκος L. Σε ποια απόσταση η
θερμοκρασία είναι μέγιστη; Θεωρήστε γνωστό ότι κάθε δαχτυλίδι του δίσκου
χάνει ισχύ (3GMṀa∕2ϖ2)![[ ]
1 - (ϖin ∕ϖ )1∕2](HEA_files/HEA487x.png) Δϖ. Επίσης ότι η συνάρτηση
f(x) = x-3
Δϖ. Επίσης ότι η συνάρτηση
f(x) = x-3![[ ]
1 - (a∕x )1∕2](HEA_files/HEA488x.png) αποκτά μέγιστη τιμή στο x = 49a∕36.
αποκτά μέγιστη τιμή στο x = 49a∕36.
(α) Δύο σημαντικές κατηγορίες αστροφυσικών δίσκων είναι οι λεπτοί δίσκοι και
οι advection-dominated accretion flows (ADAFs). Ποια είναι η διαφορά τους;
Εκπέμπουν ακτινοβολία; Με τι φάσμα;
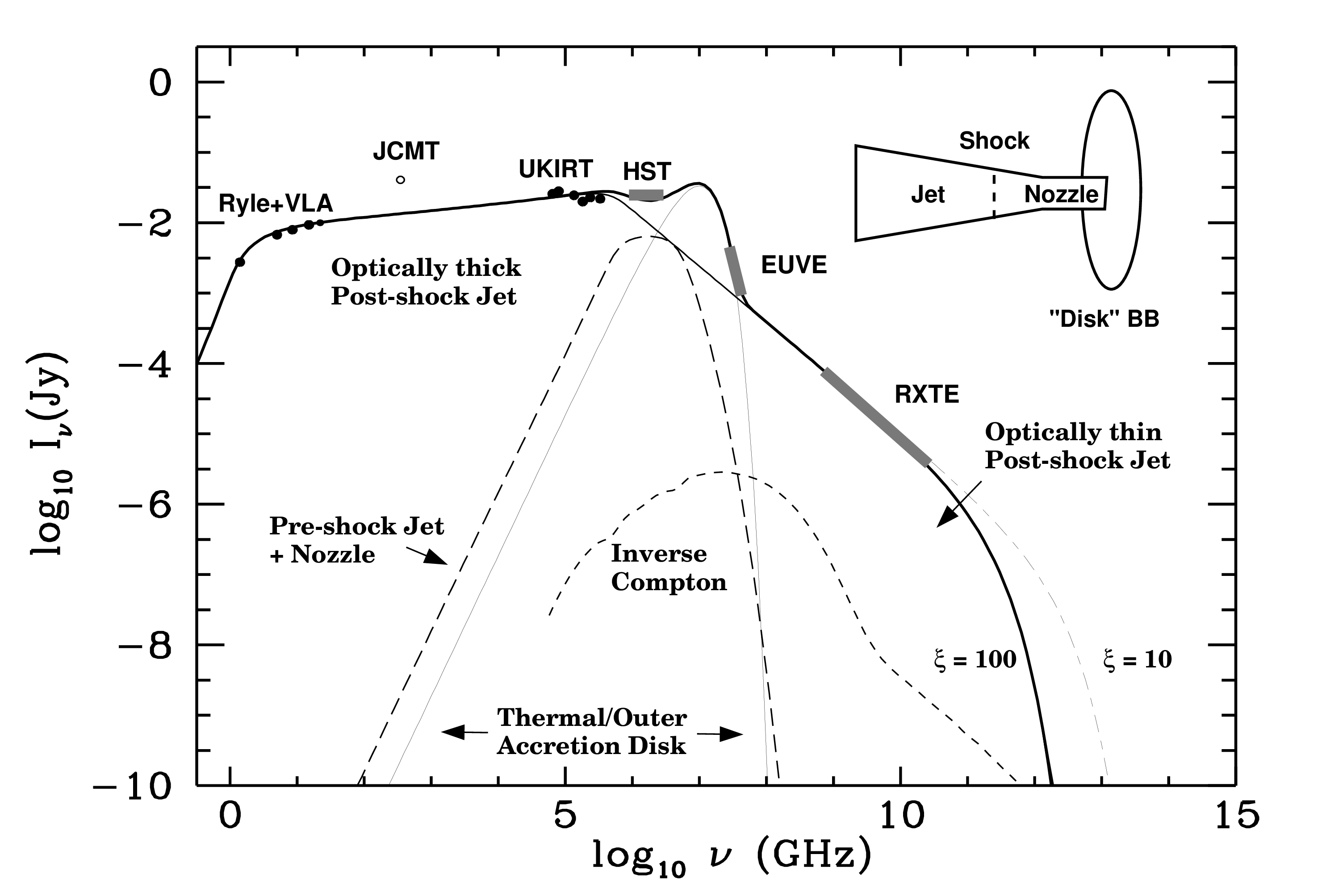
(α) Στους λεπτούς αστροφυσικούς δίσκους προσαύξησης ορίζουμε την
επιφανειακή πυκνότητα μάζας Σ. Η εξίσωση που εκφράζει τη διατήρηση μάζας
μπορεί να ολοκληρωθεί και να οδηγήσει σε μια σχέση μεταξύ του ρυθμού
προσρόφησης ύλης Ṁa, της ακτινικής ταχύτητας V ϖ και του Σ. Ποια η σχέση
αυτή; (Να αποδειχθεί.)
(β) ϒποθέτοντας υδροστατική ισορροπία στην ẑ κατεύθυνση με θερμοκρασία
ανεξάρτητη του z, και κεπλεριανή περιστροφή, δείξτε ότι H∕ϖ = Cs∕V ϕ.
(γ) Αν η απώλεια στροφορμής που αντιστοιχεί σε ρυθμό προσρόφησης Ṁa
οφείλεται σε ενεργό ιξώδες, ο αντίστοιχος συντελεστής κινηματικού ιξώδους
απαιτείται να ικανοποιεί την εξίσωση ν = (Ṁa∕3πΣ)(1 - 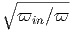 ). Το ν
βέβαια συνδέεται και με τη φυσική της τυρβώδους ροής· η σχέση αυτή δεν είναι
εύκολο να βρεθεί. Για τον λόγο αυτό οι Shakura & Sunyaev (1973, A&A, 24,
337) υπέθεσαν μια απλή εξάρτηση της μορφής ν = αCsH, κρύβοντας όλη τη
φυσική στην παράμετρο α. Οι δίσκοι στους οποίους ισχύει μια τέτοια σχέση
ονομάστηκαν α-δίσκοι. Δείξτε ότι η ταχύτητα προσρόφησης V ϖ(ϖ) σε έναν
α-δίσκο δίνεται από τη σχέση V ϖ = -
). Το ν
βέβαια συνδέεται και με τη φυσική της τυρβώδους ροής· η σχέση αυτή δεν είναι
εύκολο να βρεθεί. Για τον λόγο αυτό οι Shakura & Sunyaev (1973, A&A, 24,
337) υπέθεσαν μια απλή εξάρτηση της μορφής ν = αCsH, κρύβοντας όλη τη
φυσική στην παράμετρο α. Οι δίσκοι στους οποίους ισχύει μια τέτοια σχέση
ονομάστηκαν α-δίσκοι. Δείξτε ότι η ταχύτητα προσρόφησης V ϖ(ϖ) σε έναν
α-δίσκο δίνεται από τη σχέση V ϖ = -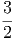
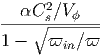 .
.
(α) Ποιοι οι πιθανοί μηχανισμοί απώλειας στροφορμής στους
αστροφυσικούς δίσκους προσαύξησης;
(β) Στους λεπτούς αστροφυσικούς δίσκους προσαύξησης ορίζουμε την
επιφανειακή πυκνότητα μάζας Σ. Η εξίσωση που εκφράζει τη διατήρηση μάζας
οδηγεί σε μια σχέση μεταξύ του Σ, του ρυθμού προσρόφησης ύλης Ṁa και της
ακτινικής ταχύτητας V ϖ. Ποια η σχέση αυτή; (Να αποδειχθεί).
(γ) Αν η απώλεια στροφορμής που αντιστοιχεί σε ρυθμό προσρόφησης Ṁa
οφείλεται σε τυρβώδη ροή, ο αντίστοιχος συντελεστής κινηματικού ιξώδους
απαιτείται να ικανοποιεί την εξίσωση ν = (Ṁa∕3πΣ)(1 -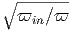 ).
).
Συνδυάζοντας την παραπάνω σχέση με τη διατήρηση της μάζας, δείξτε ότι το
ν είναι της τάξης ϖ|V ϖ|.
΄Εστω λεπτός αστροφυσικός δίσκος προσαύξησης με ρυθμό προσρόφησης
μάζας Ṁa, γύρω από κεντρικό σώμα μάζας M.
(α) Από κάθε δαχτυλίδι του δίσκου πάχους Δϖ, χάνεται μηχανική ισχύς
3GMṀaΔϖ∕2ϖ2. Αν αυτή ακτινοβολείται με φάσμα μέλανος σώματος ποια η
ενεργός θερμοκρασία του δίσκου σαν συνάρτηση της ακτίνας;
(β) Αν η θερμοκρασία του αερίου του δίσκου είναι ίση με την ενεργό
θερμοκρασία, ποια η εξάρτηση του Cs από την ακτίνα, δηλ. ποιος ο εκθέτης
q στη σχέση Cs ∝ ϖq; Ποια η εξάρτηση του H(ϖ) = C
s∕Ω από την ακτίνα,
δηλ. ποιος ο εκθέτης q′ στη σχέση H ∝ ϖq′; Σχεδιάστε πρόχειρα το σχήμα
του δίσκου.
(γ) Αν η απώλεια στροφορμής που αντιστοιχεί σε ρυθμό προσρόφησης Ṁa
οφείλεται σε τυρβώδη ροή, ο αντίστοιχος συντελεστής κινηματικού ιξώδους
ν απαιτείται να ικανοποιεί την εξίσωση Ṁa = 3πνΣ, όπου Σ η επιφανειακή
πυκνότητα μάζας. Σε α-δίσκους, όπου ν = αCsH με α = σταθερά < 1, βρείτε
πώς εξαρτάται η επιφανειακή πυκνότητα Σ από την ακτίνα (βρείτε τον αντίστοιχο
εκθέτη). Πώς εξαρτάται η πυκνότητα ρ και η πίεση P από την ακτίνα;
(δ) Η εξίσωση που εκφράζει τη διατήρηση μάζας οδηγεί σε μια σχέση μεταξύ του
Σ, του Ṁa και της ακτινικής ταχύτητας V ϖ. Ποια η σχέση αυτή; (Να αποδειχθεί).
Συνδυάζοντας τη σχέση αυτή με την Ṁa = 3πνΣ δείξτε ότι σε α-δίσκους ισχύει
V ϖ∕Cs = -1.5 αCs∕V ϕ. Παρατηρήστε ότι σε λεπτούς δίσκους |V ϖ|« Cs.
(ε) Η εξίσωση της ορμής στην  κατεύθυνση είναι
κατεύθυνση είναι
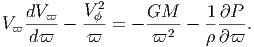
Αντιστοιχίστε διαστατικά κάθε όρο με μέγεθος της μορφής (…)2∕ϖ όπου
(…) κάποια χαρακτηριστική ταχύτητα. Στη συνέχεια κατατάξτε τους όρους από
περισσότερο σε λιγότερο σημαντικούς.
Κρατώντας τους δυο πιο σημαντικούς όρους προκύπτει ότι V ϕ∕ϖ ≡ Ω ≈ ΩK =
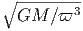 , δηλ. ότι το ρευστό περιστρέφεται κεπλεριανά. Κρατήστε ακόμα
έναν όρο (τον πιο σημαντικό από τους υπόλοιπους) για να απαντήσετε αν η
περιστροφή είναι υπο- ή υπερ-κεπλεριανή. Ποια η σχετική διαφορά |Ω-ΩK|∕ΩK;
Είναι σημαντική;
, δηλ. ότι το ρευστό περιστρέφεται κεπλεριανά. Κρατήστε ακόμα
έναν όρο (τον πιο σημαντικό από τους υπόλοιπους) για να απαντήσετε αν η
περιστροφή είναι υπο- ή υπερ-κεπλεριανή. Ποια η σχετική διαφορά |Ω-ΩK|∕ΩK;
Είναι σημαντική;
(α) Ποιοι είναι οι πιθανοί μηχανισμοί απώλειας στροφορμής στους
αστροφυσικούς δίσκους;
(β) ΄Εστω λεπτός αστροφυσικός δίσκος προσαύξησης στον οποίο δεν ισχύει
η προσέγγιση της ισόθερμης κατάστασης P(ϖ,z) = ![[Cs(ϖ )]](HEA_files/HEA496x.png) 2ρ(ϖ,z), αλλά
ισχύει η γενικότερη πολυτροπική σχέση P(ϖ,z) = Q(ϖ)
2ρ(ϖ,z), αλλά
ισχύει η γενικότερη πολυτροπική σχέση P(ϖ,z) = Q(ϖ)![[ρ(ϖ, z)]](HEA_files/HEA497x.png) Γ με
πολυτροπικό δείκτη Γ = 1 + 1∕n. Δείξτε ότι η πυκνότητα έχει τη μορφή
Γ με
πολυτροπικό δείκτη Γ = 1 + 1∕n. Δείξτε ότι η πυκνότητα έχει τη μορφή
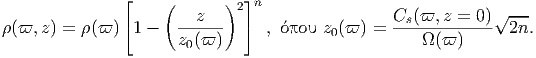
(Θεωρήστε το μαγνητικό πεδίο αμελητέο. Η ταχύτητα του ήχου είναι
Cs = 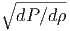 .) Ποια η φυσική σημασία των z0(ϖ) και ρ(ϖ);
.) Ποια η φυσική σημασία των z0(ϖ) και ρ(ϖ);
(α) Ποιο το πρόβλημα στροφορμής στους αστροφυσικούς δίσκους;
(β) Αναφέρατε τους δυο πιο σημαντικούς μηχανισμούς που προσφέρουν λύση
στο πρόβλημα.
(γ) Πόση είναι η ενέργεια που απελευθερώνεται ανά μονάδα χρόνου σε
έναν δίσκο εσωτερικής ακτίνας ϖin και ρυθμού προσρόφησης Ṁa γύρω από
κεντρικό σώμα μάζας M; Τι μπορεί να γίνεται αυτή η ενέργεια; Εκτιμήστε
την απελευθερούμενη ενέργεια ανά μονάδα χρόνου αν το κεντρικό σώμα
είναι συμπαγές (οπότε ο δίσκος εκτείνεται σε αποστάσεις κοντά στην ακτίνα
Schwarzschild) και ο ρυθμός προσρόφησης είναι 1M⊙ yr-1 = 2 × 1033g yr-1.
Αναφέρατε χωρίς απόδειξη από πού προκύπτουν οι επόμενες σχέσεις για
δίσκους
προσαύξησης: ϖρHV ϖ = -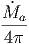 , V ϕ2 =
, V ϕ2 = 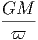 , ṀaϖV ϕ
, ṀaϖV ϕ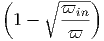 =
|T|, P =
=
|T|, P = 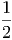 ρH2
ρH2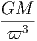 , q+ = q- =
, q+ = q- = 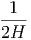
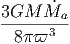
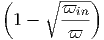 .
.
Η ροή ακτινοβολίας από έναν λεπτό αστροφυσικό δίσκο προσαύξησης, ο
οποίος εκπέμπει σαν μέλαν σώμα, είναι Fν = 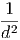 ∫
ϖinϖout
Iν2πϖdϖ cos i,
όπου Iν =
∫
ϖinϖout
Iν2πϖdϖ cos i,
όπου Iν = ![2hν3
----[--c2--]----
exp --hν-- - 1
kBT (ϖ )](HEA_files/HEA509x.png) , T(ϖ) =
, T(ϖ) = 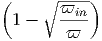 1∕4
1∕4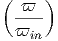 -3∕4T
0 και
T0 =
-3∕4T
0 και
T0 = 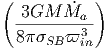 1∕4.
1∕4.
(α) Τι εκφράζουν τα διάφορα μεγέθη που περιέχονται στις παραπάνω σχέσεις;
(Ζητείται απλή αναφορά του μεγέθους που παριστά κάθε σύμβολο.)
(β) Η ροή μπορεί να γραφεί σαν
![( )3 ∫ ϖ
-hν-- ϖoiutn---------------wdw-----------------
Fν = F0 kBT0 1 [-hν- 3∕4 -1∕2 -1∕4] ,
exp kBT0w (1 - w ) - 1](HEA_files/HEA513x.png)
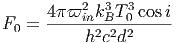
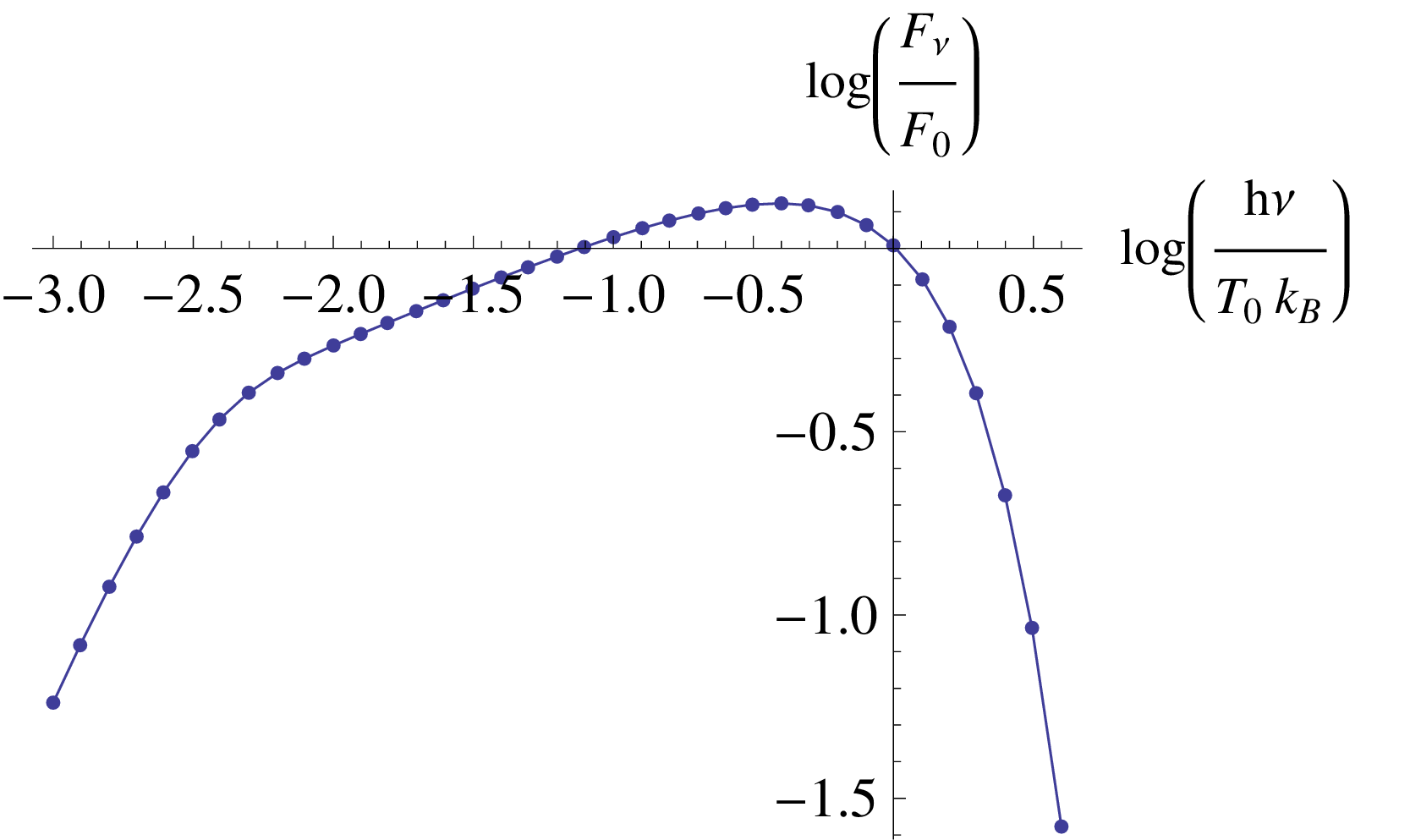
(α) Δείξτε ότι το γωνιακό άνοιγμα H∕ϖ των λεπτών δίσκων προσαύξησης
είναι της τάξης Cs∕V ϕ. Αναφέρατε όλες τις υποθέσεις που οδηγούν σε αυτήν
τη σχέση.
(β) Δείξτε ότι η ταχύτητα περιστροφής στους λεπτούς δίσκους προσαύξησης
είναι ελάχιστα υπο-κεπλεριανή. Συγκεκριμένα ότι V ϕ ≈ 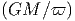 1∕2
1∕2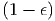 ,
όπου το ϵ είναι της τάξης H2∕ϖ2.
,
όπου το ϵ είναι της τάξης H2∕ϖ2.
Δίνονται οι προσεγγιστικές εκφράσεις των συνιστωσών της εξίσωσης ορμής σε
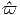 και ẑ διεύθυνση
και ẑ διεύθυνση
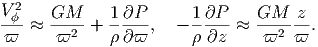
(α) Ποιοι είναι οι επικρατέστεροι μηχανισμοί απώλειας στροφορμής στους
αστροφυσικούς δίσκους προσαύξησης;
(β) Από κάθε δαχτυλίδι ενός δίσκου, πάχους Δϖ και συνολικής επιφάνειας 2×
2πϖ Δϖ, χάνεται μηχανική ισχύς 3GMṀaΔϖ∕2ϖ2. Αν αυτή ακτινοβολείται
με φάσμα μέλανος σώματος ποια η ενεργός θερμοκρασία του δίσκου σαν
συνάρτηση της ακτίνας;
(γ) Αν η μηχανική ισχύς 3GMṀaΔϖ∕2ϖ2, αντί να ακτινοβολείται, εκλύεται
σαν ροή Poynting εκτιμήστε την ένταση του μαγνητικού πεδίου και δώστε την
εξάρτησή της από την ακτίνα.
(α) Αναφέρατε τις πέντε εξισώσεις που περιγράφουν ένα υδροδυναμικό
ρευστό (οι οποίες, εφόσον λυθούν, δίνουν τις ρ, P, V ).
(β) ΄Οταν τις εφαρμόσουμε σε έναν λεπτό και ισόθερμο αστροφυσικό δίσκο
προσαύξησης, ποιες από αυτές δίνουν (β1) τον ρυθμό προσρόφησης μάζας, (β2)
τον κεπλεριανό νόμο περιστροφής και (β3) την υδροστατική ισορροπία κάθετα
στο επίπεδο του δίσκου; (Δεν ζητείται απόδειξη, παρά μόνο η αντιστοιχία με
τις εξισώσεις).
(γ) Ποιο το γωνιακό άνοιγμα H∕ϖ ενός λεπτού και ισόθερμου δίσκου
προσαύξησης συναρτήσει της ταχύτητας ήχου και της περιστροφικής ταχύτητάς
του; (Ζητείται απόδειξη της σχέσης αυτής).
΄Εστω δίσκος με ρυθμό προσαύξησης Ṁ, γύρω από συμπαγές σώμα μάζας
M.
(α1) Πόση η συνολική ισχύς L μηχανικής ενέργειας που απελευθερώνεται αν
ο δίσκος εκτείνεται από ϖin μέχρι ϖout » ϖin; Ποια η αντίστοιχη απόδοση
L∕Ṁc2; Δώστε τις τιμές της για (i) έναν αστέρα νετρονίων με M = 1.4M
⊙,
R = 10 km, (ii) έναν λευκό νάνο με M = 0.6M⊙, R = 109 cm, (iii) μια
μέγιστα περιστρεφόμενη μελανή οπή στην οποία ο δίσκος εκτείνεται μέχρι
ϖin = GM∕c2, (iv) μια μη-περιστρεφόμενη μελανή οπή στην οποία ο δίσκος
εκτείνεται μέχρι ϖin = 6GM∕c2. (Συγκρίνετε με την απόδοση πυρηνικής
σύντηξης 0.007).
(α2) Στο κέντρο του Γαλαξία μας υπάρχει μελανή οπή (Sgr A⋆) με μάζα
M = 4 × 106M
⊙, η οποία προσροφά ύλη με ρυθμό Ṁ = 10-5M
⊙∕yr. Από
την περιοχή της παίρνουμε ολική λαμπρότητα Lbol = 3 × 1033 erg/s (παρότι
υπάρχουν ενδείξεις ότι στο παρελθόν ήταν μέχρι και ένα εκατομμύριο φορές
μεγαλύτερη). Είναι η απόδοση παρόμοια με την αντίστοιχη του προηγούμενου
ερωτήματος για μελανές οπές; Αν όχι, πού μπορεί να οφείλεται αυτό;
(β1) Πόση είναι η μηχανική ισχύς που απελευθερώνεται σε έναν δίσκο
προσαύξησης καθώς υλικό μετακινείται από την ακτίνα ϖ + dϖ στην ακτίνα
ϖ; Θεωρώντας ότι ο δίσκος είναι μέλαν σώμα και ότι η παραπάνω ισχύς
ακτινοβολείται από την επιφάνεια του δίσκου μεταξύ των ακτίνων ϖ και ϖ+dϖ,
βρείτε την ενεργό θερμοκρασία.
(β2) Η παραπάνω θεώρηση δεν είναι ακριβής γιατί υποθέτει ότι η μηχανική
ενέργεια εκπέμπεται σαν ακτινοβολία τοπικά, ενώ γενικά το ενεργό ιξώδες
μπορεί να ανακατανείμει την ενέργεια μέσα στον δίσκο. Το ακριβέστερο
αποτέλεσμα έχουμε δείξει ότι είναι
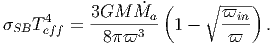
Το blazar 1 ES 1218+30.4 έχει ερυθρομετατόπιση z = 0.182 και άρα βρίσκεται σε απόσταση d = cz∕H, όπου H = 75 km s-1 Mpc-1 η σταθερά του Hubble. Η κεντρική μελανή του οπή έχει μάζα M = 108M ⊙ ενώ το φάσμα του είναι το ακόλουθο:
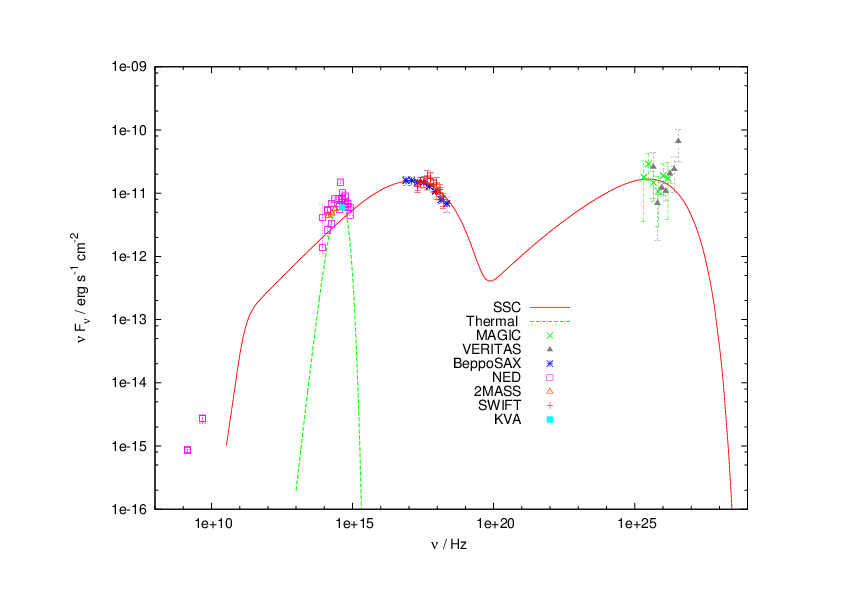
(α) Ποιοι είναι οι επικρατέστεροι μηχανισμοί απώλειας στροφορμής στους
αστροφυσικούς δίσκους προσαύξησης;
(β) ΄Εστω αστροφυσικός δίσκος προσαύξησης γύρω από κεντρικό σώμα μάζας
M, με εσωτερική ακτίνα ϖin = ηGM∕c2, στον οποίο ο ρυθμός πρόσπτωσης
μάζας είναι Ṁa. Πόση ενέργεια ανά χρόνο απελευθερώνεται από τον δίσκο αυτό;
Σχολιάστε το αποτέλεσμα για δίσκο γύρω από (1) περιστρεφόμενη μελανή οπή
Kerr, (2) μη-περιστρεφόμενη μελανή οπή Schwarzschild, (3) νεογέννητο άστρο.
(γ) ΄Εστω ένα μέρος της ενέργειας που απελευθερώνεται από τον δίσκο
τροφοδοτεί έναν πίδακα πλάσματος στον οποίο εκρέει ύλη με ρυθμό Ṁw και
επιταχύνεται σε παράγοντα Lorentz γ∞. Δείξτε ότι ο λόγος Ṁa∕Ṁw είναι
μεγαλύτερος από 2ηγ∞.
(α) Σε ένα λεπτό, ισόθερμο αστροφυσικό δίσκο προσαύξησης δείξτε ότι η
πυκνότητα ελαττώνεται εκθετικά με το ύψος από το ισημερινό επίπεδο, δηλ.
ρ = ρ0(ϖ)e-z2∕H2 με κατάλληλο H(ϖ), το οποίο και να βρείτε.
(β) Πόση είναι η μάζα ανά επιφάνεια του δίσκου Σ = ∫
-∞∞ρ dz; Πόσο καλή
είναι η προσέγγιση Σ ≈ 2Hρ0;
(γ) Αν γνωρίζουμε την επιφανειακή πυκνότητα Σ(ϖ) και το ρυθμό
προσρόφησης της ύλης Ṁa, ποια είναι η ακτινική ταχύτητα V ϖ σε κάθε ακτίνα
ϖ;
(δ) Τι ρόλο μπορεί να παίζει η τύρβη στους αστροφυσικούς δίσκους; Τι εκφράζει
η σχέση ν = 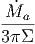 ; Μέσω αυτής δείξτε ότι η ακτινική ταχύτητα V ϖ έχει μέτρο
συγκρίσιμο με
; Μέσω αυτής δείξτε ότι η ακτινική ταχύτητα V ϖ έχει μέτρο
συγκρίσιμο με 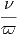 .
.
Δίνεται ∫
-∞∞e-x2
dx = 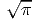 .
.
Longair, M. S. (2011). High Energy Astrophysics. Cambridge University Press, 3rd
edition.
Krolik, J. H. (1999). Active Galactic Nuclei: From the Central Black Hole to the
Galactic Environment. Princeton University Press.
Frank, J., King, A., Raine, D. (2002). Accretion Power in Astrophysics.
Cambridge University Press, 3rd edition.
Shakura, N. I. & R. A. Sunyaev, (1973). “Black holes in binary systems.
Observational appearance.”. Astronomy and Astrophysics, 24, 337.
Οι εξισώσεις στα προηγούμενα κεφάλαια είναι γραμμένες στο σύστημα Gauss.1
Πολλές εξισώσεις ηλεκτρομαγνητισμού έχουν διαφορετική μορφή αναλόγως του αν χρησιμοποιούμε μονάδες SI 2 ή Gauss . Αν ξέρουμε έναν τύπο στο σύστημα SI μπορούμε να τον γράψουμε στο Gauss αν και στα δυο μέλη αντικαταστήσουμε τα σύμβολα στη στήλη «SI» του πίνακα 11.1 με τα σύμβολα της στήλης «Gauss». Το αντίστροφο επίσης ισχύει αν θέλουμε να μετατρέψουμε έναν τύπο από το Gauss στο SI.
| Ποσότητα | Gauss | SI |
| ταχύτητα φωτός | c | 1∕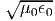 |
| ηλεκτρικό πεδίο | E∕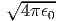 | E |
| ηλεκτρικό δυναμικό | V∕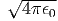 | V |
| ηλεκτρική μετατόπιση | 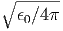 D D | D |
| πυκνότητα φορτίου | 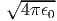 ρ ρ | ρ |
| φορτίο | 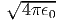 q q | q |
| πυκνότητα ρεύματος | 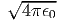 J J | J |
| ρεύμα | 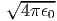 I I | I |
| ηλεκτρική πόλωση | 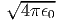 P P | P |
| μαγνητικό πεδίο | 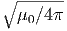 B B | B |
| διανυσματικό δυναμικό | 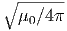 A A | A |
| πεδίο H | H∕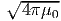 | H |
| μαγνήτιση | 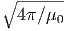 M M | M |
| ειδική αγωγιμότητα | 4πϵ0 σ | σ |
| διηλεκτρική σταθερά | ϵ0ϵ | ϵ |
| μαγνητική διαπερατότητα | μ0μ | μ |
| αντίσταση | R∕4πϵ0 | R |
| εμπέδηση | Z∕4πϵ0 | Z |
| συντελεστής αυτεπαγωγής | L∕4πϵ0 | L |
| χωρητικότητα | 4πϵ0 C | C |
Τυχόν γινόμενα ϵ0μ0 που θα εμφανιστούν μετά τις αντικαταστάσεις τα αντικαθιστούμε με 1∕c2 (αφού c2ϵ 0μ0 = 1).
Παραδείγματα:
΄Εστω ότι θέλουμε να γράψουμε στο Gauss τον τύπο της δύναμης έλξης δυο
φορτίων που στο SI δίνεται από τη σχέση F = (1∕4πϵ0)q1q2∕r2. Αντικαθιστούμε τα
φορτία q1, q2 με 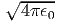 q1,
q1, 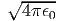 q2 (τα υπόλοιπα μεγέθη δεν υπάρχουν στον
πίνακα 11.1 και άρα τα αφήνουμε ως έχουν) και βρίσκουμε F = q1q2∕r2.
q2 (τα υπόλοιπα μεγέθη δεν υπάρχουν στον
πίνακα 11.1 και άρα τα αφήνουμε ως έχουν) και βρίσκουμε F = q1q2∕r2.
Ο νόμος του Gauss στο σύστημα Gauss γράφεται ∇⋅E = 4πρ∕ϵ, όπου ρ η
πυκνότητα φορτίου. Σύμφωνα με τον πίνακα 11.1, για να βρούμε τον τύπο
στο SI, πρέπει να αντικαταστήσουμε το E∕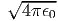 με E, το
με E, το 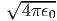 ρ με ρ
και το ϵ0ϵ με ϵ. Γι΄ αυτό, ξαναγράφουμε τον τύπο στο σύστημα Gauss σαν
∇⋅ (E∕
ρ με ρ
και το ϵ0ϵ με ϵ. Γι΄ αυτό, ξαναγράφουμε τον τύπο στο σύστημα Gauss σαν
∇⋅ (E∕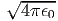 ) =
) = 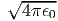 ρ∕ϵ0ϵ και μετά τις αντικαταστάσεις βρίσκουμε τον τύπο
στο SI ∇⋅E = ρ∕ϵ.
ρ∕ϵ0ϵ και μετά τις αντικαταστάσεις βρίσκουμε τον τύπο
στο SI ∇⋅E = ρ∕ϵ.
Το πεδίο H στο SI δίνεται από H = B∕μ0 -M. Στο Gauss ο προηγούμενος τύπος γίνεται H = B - 4πM.
Ο πίνακας 11.2 μπορεί να χρησιμοποιηθεί για τη μετατροπή μονάδων από το ένα σύστημα στο άλλο.
| Ποσότητα | SI | Gauss |
| μήκος | 1 m | 102 cm |
| μάζα | 1 kg | 103 g |
| χρόνος | 1 s | 1 s |
| συχνότητα | 1 Hz | 1 Hz |
| δύναμη | 1 N | 105 dynes |
| έργο | 1 J | 107 ergs |
| ενέργεια | 1 J | 107 ergs |
| ισχύς | 1 W | 107 ergs s-1 |
| φορτίο | 1 Cb | 3 × 109 statcoulombs |
| πυκνότητα φορτίου | 1 Cb m-3 | 3 × 103 statcoul cm-3 |
| ρεύμα | 1 A | 3 × 109 statamperes |
| πυκνότητα ρεύματος | 1 A m-2 | 3 × 105 statamp cm-2 |
| ηλεκτρικό πεδίο | 1 V m-1 | 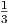 × 10-4 statvolt cm-1 × 10-4 statvolt cm-1 |
| ηλεκτρικό δυναμικό | 1 V | 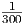 statvolt statvolt |
| ηλεκτρική πόλωση | 1 Cb m-2 | 3 × 105 dipole moment cm-3 |
| ηλεκτρική μετατόπιση | 1 Cb m-2 | 12π × 105 statcoul cm-2 |
| ειδική αγωγιμότητα | 1 Ω-1 m-1 | 9 × 109 s-1 |
| αντίσταση | 1 Ω | 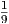 × 10-11 s cm-1 × 10-11 s cm-1 |
| χωρητικότητα | 1 F | 9 × 1011 cm |
| μαγνητική ροή | 1 Wb | 108 G cm2 ή maxwells |
| μαγνητικό πεδίο | 1 T | 104 G |
| πεδίο H | 1 A m-1 | 4π × 10-3 Oe |
| μαγνήτιση | 1 A m-1 | 10-3 magnetic moment cm-3 |
| συντελεστής αυτεπαγωγής | 1 H | 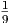 × 10-11 × 10-11 |
Σε όλα τα πολλαπλάσια του 3 του πίνακα αυτού (εκτός των εκθετών), ακριβέστερες τιμές βρίσκονται αν αντικατασταθεί το 3 με 2.99792458 (αυτό προκύπτει από την αριθμητική τιμή της ταχύτητας του φωτός που είναι 2.99792458 × 1010 cm s-1 αντί της προσεγγιστικής τιμής 3 × 1010 cm s-1).
Για παράδειγμα 1 Ω-1 m-1 = 8.987551787 × 109 s-1 αντί του προσεγγιστικού 9(= 32) × 109 s-1.
Οι τιμές διαφόρων φυσικών σταθερών στο σύστημα Gauss δίνονται στον πίνακα 11.3.
| ταχύτητα φωτός | c = 2.997925 × 1010 |
| σταθερά παγκόσμιας έλξης | G = 6.6732 × 10-8 |
| σταθερά Planck | h = 6.625 × 10-27 |
| μάζα ηλεκτρονίου | me = 9.10956 × 10-28 |
| φορτίο ηλεκτρονίου | e = 4.80325 × 10-10 |
| ηλεκτρονιοβόλτ | eV = 1.602192 × 10-12 |
| μάζα πρωτονίου | mp = 1.672614 × 10-24 |
| σταθερά λεπτής υφής | e2∕ℏc = 1∕137.036 |
| διατομή Thomson | σT = 0.665245 × 10-24 |
| σταθερά Boltzmann | kB = 1.38062 × 10-16 |
| σταθερά ακτινοβολίας | αBB = 7.5641 × 10-15 |
| έτος | yr = 3.155815 × 107 |
| αστρονομική μονάδα | AU = 1.495985 × 1013 |
| parsec | pc = 3.0856 × 1018 |
| μάζα του ήλιου | M⊙ = 1.989 × 1033 |
| ακτίνα του ήλιου | R⊙ = 6.96 × 1010 |
| λαμπρότητα του ήλιου | L⊙ = 3.9 × 1033 |
| μάζα της γης | = 5.977 × 1027 |
| ισημερινή ακτίνα της γης | = 6.3782 × 108 |
| μέση ακτίνα της γης | = 6.37103 × 108 |
| επιτάχυνση βαρύτητας στην επιφάνεια της γης | = 9.80665 × 102 |
| ακτίνα Bohr στο άτομο του υδρογόνου | = 0.5292 × 10-8 |
Jackson, J. D. (1998). Classical Electrodynamics. John Wiley & Sons Inc.